关于高等数学中两个问题的探讨
司志本, 李春光
(1.河北民族师范学院 初等教育系,河北 承德 067000 2.河北民族师范学院 科研处,河北 承德 067000)
关于高等数学中两个问题的探讨
司志本1, 李春光2
(1.河北民族师范学院 初等教育系,河北 承德 067000 2.河北民族师范学院 科研处,河北 承德 067000)
分段函数和积分上限函数,是高等数学中比较重要的两类函数.分段函数在分界点处的导数和积分,是学生感到比较棘手的内容,这就需要教师在内容的解读以及教学方法的选取上,要根据学生的实际情况进行科学的处理;积分上限函数,是一个用积分形式给出的函数,深入挖掘这个函数的潜在功能,对于学生深刻理解微积分的概念是十分有益的.
分段函数;积分上限函数;导数;积分
在高等数学中,有许多内容都要涉及到分段函数和积分上限函数,而学生在解决这两类函数的相关问题时,往往会感到无从下手.本文将对这两类函数的相关问题做一点探讨,相信对学生能够起到一定的指导作用.
1. 关于分段函数的导数和积分
分段函数是一类常见的并且十分重要的函数,它的明显特征就是“分段”,它在分界点处的一些运算和性质,对于初学者来说,需要谨慎处理.
1.1 对分段函数定义的理解
分段函数是指在自变量的不同变化范围中,对应法则用不同式子来表示的函数(注:本文中的分段函数均指一元函数)。分段函数虽然有时也可以用一个式子表示出来,例如,分段函数可以用一个式子表示为但是,为了研究方便,我们往往还是用几个表达式来表示,而不刻意追求形式上的简单.
我们知道,初等函数在它的定义区间内是连续的.因为分段函数的分段点往往是间断点,所以,在有些情况下,分段函数在整个定义区间上不是初等函数.
因为分段函数的关键特征是“分段”,所以,在一般情况下,分段函数的图象是由若干段曲线组成的.例如,函数
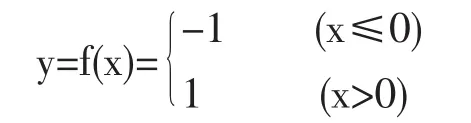
的图象是以点(0,-1)和点(0,1)(不含此点)为始点,分别向左和向右的两条水平射线.
1.2 分段函数的导数
一般来说,求分段函数的导数可以分两步进行,第一步,先求出函数在去掉分界点以后的各个区间上的导数;第二步,再研究函数在分界点处的导数情况.在各个小区间上的导数可以根据导数的定义、公式和性质等,采用多种方法去求;而在分界点处的导数,一般需要先研究函数在该点的单侧导数(左导数和右导数).具体说来,如果在该点存在单侧导数,那么就先求出函数在该点处的单侧导数;然后再根据单侧导数的情况,判断函数在该点是否可导;若可导,再进一步求出导数.
解:先将函数f(x)写为分段函数的形式.

当x>0时,有f′(x)=1;当x<0时,有f′(x)=-1;当x=0时,由左、右导数的定义有

因为f-′(0)≠f+′(0),所以,函数在x=0点处不可导.
有时也可以根据导数定义直接求出函数在分界点处的导数.
解:当x≠0时,有

当x=0时,由导数定义有

1.3 分段函数的不定积分
在求分段函数的不定积分时,首先要求出分段函数在各个小区间上的不定积分,这些积分中包含着若干个积分常数,如果被积函数在所有的分界点都是连续的,那么就可以根据不定积分(原函数)的连续性,找出这些积分常数之间的关系,最后得到只含有一个积分常数的不定积分;如果被积函数在某些分界点不连续,那么最后的积分结果可能不止含有一个积分常数,而是含有几个独立的积分常数.
因为被积函数f(x)在区间(-∞,+∞)上连续,所以,根据原函数的定义可知,f(x)的原函数也在该区间上连续.

在例3中,因为f(x)在整个定义区间(-∞,+∞)上是连续的,所以,最后的积分结果中只含有一个积分常数.
解:容易知道,分段点x=0是f(x)的第一类间断点(即函数f(x)在x0点的左右极限都存在);分段点x=1是f(x)的连续点.先分别求出f(x)在区间(-∞,0),(0,1)和(1,+∞)上的不定积分:


由例4可知,在分段函数的不定积分中,如果分段点是不连续点,则积分常数可能不止一个.
1.4 分段函数的定积分
与不定积分相比较,分段函数的定积分就显得简单多了.定积分的定义告诉我们,有限个间断点不影响定积分的值,所以,只要分段函数的定积分存在,我们就可以以分界点为界点,把原积分区间划分为若干个小的积分区间,先求出函数在每一个小区间上的定积分,然后再对这些积分值求和即可.
解:将被积函数写为分段函数的形式:
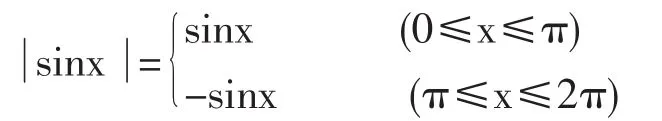
以x=π为界点,将积分区间[0,2π]拆为两个小区间[0,π],[π,2π],则有
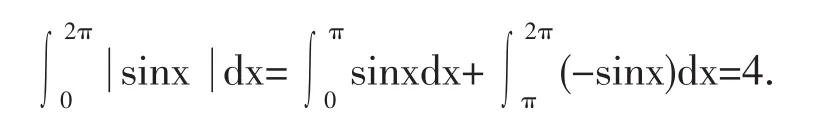
2. 关于积分上限函数的导数
积分上限函数,是一个用积分形式给出的函数,深入挖掘这个函数的潜在功能,对于深入理解微分和积分的概念是十分有益的.我们先给出积分上限函数的定义以及与之相关的一个定理.
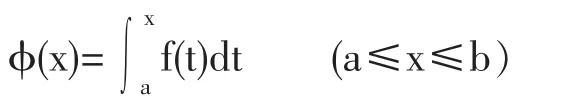
为积分上限函数,也称变上限函数.
定理:若函数f(x)在区间[a,b]上连续,则积分上限函数
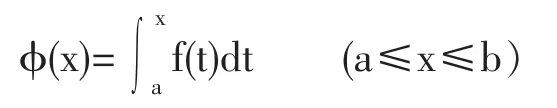
在[a,b]上可导,其导数为

2.1 几个积分表达式
上面的(*)式体现了积分上限函数的一个明显特征:即对一个函数先积分后微分,其作用相互抵消.这个特征可以看作是不定积分性质的一种推广.受(*)式启发,我们从一个基本的积分表达式出发,把这个积分中三个含t的位置,分别用一个x,两个x,三个x替换,对于得到的表达式再分别对x和t求导,研究一下这些导数的情况.在下面的讨论中,我们假设所涉及的f(x)的导数和积分都是存在的.
最基本的积分为(三个位置都是t,不含x):

把(1)式中1个位置的t换为x,可以得到下面三个积分:
CRISPR/Cas9系统也有局限性。如存在一定的脱靶效应。CRISPR/Cas9系统的特异性取决于sgRNA上的识别序列。为了避免脱靶效应,有必要将Cas9引导至其基因组中精确靶标的sgRNA。为了确保Cas9的靶向活性和正常功能,使用Ⅱ型CRISPR/Cas系统和Cas9表征的研究已经证明需要与靶基因序列完美匹配[26-28]。有学者研发了很多软件辅助CRISPR/Cas9系统快速筛选特定基因序列靶点,有针对性地避开可能脱靶的位点,从而降低甚至消除脱靶现象[29]。

把(1)式中2个位置的t换为x,可以得到下面三个积分:
把(1)式中的三个t都换为x,可以得到下面一个积分:

把(1)式中的积分上限换为常数a,可以得到下面一个积分:

2.2 对x的导数
现在我们分别讨论上面9个积分对x的导数。

(2)式中的积分对x的导数,上面的定理给出了结论,即


(4)式中的积分变量是x,因此,这个积分实际上是被积函数为常数的定积分,即

(5)式中的积分变量是t,被积函数f(x)可以视为常数,即再对x求导,则有

(6)式中的积分变量是x,被积函数f(t)可以视为常数,即它对x的导数为


(8)式中的积分变量是x,从本质上讲,与(1)式没区别,但是,这个积分结果是x的函数,所以,对x的导数为

其中,F(x)是f(x)的一个原函数.
(9)式中的a是一个常数,这个积分就是通常意义下的定积分,其积分结果是一个常数,所以,对x求导的结果是0,即

3. 对t的导数
关于(1)—(9)式中的9个积分对t的导数,完全可以仿照上面的方法进行讨论,其结果与对x求导的结果十分相似,此处不再赘述.
[1]华东师范大学数学系.高等数学(上)[M].上海:华东师范大学出版社,1998,(8)
[2]西北工业大学高等数学教研室.高等数学中的典型问题与解法[M].上海:同济大学出版社,2001,(6)
[3]吕通庆.数学分析中一些重要概念及其矛盾概念[M].北京:高等教育出版社,1979,(3)
O13
A
2095-3763(2012)02-0073-03
2011-11-20
司志本(1959-),男,河北兴隆人,河北民族师范学院初等教育系教授。

