OFDM/OQAM系统自适应波形设计及多址接入系统
胡 苏 武 刚 李少谦
(电子科技大学通信抗干扰国家级重点实验室 成都 610054)
1 引言
正交频分复用(OFDM)利用不同子载波正交特性达到系统频谱效率最大化,所以被认为是未来无线通信传输与多址接入的框架技术[1]。尽管传统OFDM系统通过添加循环前缀(Cyclic Prefix,CP)能够有效地消除多径干扰,CP-OFDM系统仍然存在不足之处:(1)OFDM系统固有的sinc函数旁瓣较高,导致系统对频率偏移敏感;(2)尽管添加循环前缀能够消除多径干扰的影响,但降低了CP-OFDM系统频谱利用率。
若采取与传统 CP-OFDM 不同的设计思路,OFDM 系统利用成形滤波器的时间频率聚焦优化特性,在不添加循环前缀的前提下,具有抑制字符间干扰(Inter Symbol Interference,ISI)和子载波间干扰(Inter Carrier Interference,ICI)的能力,提高无线通信系统的传输性能以及频谱利用率[2-5]。现有研究表明,各向同性正交变换算法(Isotropic Orthogonal Transform Algorithm,IOTA)在时间域和频率域均具有良好的聚焦特性[6-8]。然而,IOTA函数仅仅满足实数域正交条件的特性,使基于IOTA函数的 OFDM 系统必须采用交错正交幅度调制方式(Offset QAM),即基于交错正交幅度调制的正交频分复用系统(OFDM/Offset QAM,OFDM/OQAM)。近来,基于IOTA函数的OFDM/OQAM系统已成为IEEE 802.22 WRAN的技术标准草案备选方案之一[9]。
对于无线通信系统而言,理想的成形滤波器应满足在时间域与频率域都快速滚降的特性,抑制ISI和ICI对无线通信系统的影响。然而,在时间域与频率域同时具有快速滚降特性的理想成形滤波器并不存在。根据成形滤波器优化设计理论,OFDM系统可以根据无线信道传输环境选择合适的成形滤波器,例如信道散射函数[4]。由于IOTA函数并不具备时间、频率聚焦可调特性,因此基于IOTA函数的OFDM/OQAM系统不能够在任何无线传输信道条件下取得最优性能。本文从正交频分复用系统优化理论出发,分析基于IOTA函数的OFDM/OQAM系统不足,讨论基于扩展高斯函数(Extended Gauss Function,EGF)的OFDM/OQAM系统。最后,结合基于EGF函数的OFDM/OQAM系统具有无线信道匹配的优点,扩展至基于EGF函数的正交频分多址接入系统(Orthogonal Frequency Division Multiple Access/Offset QAM,OFDMA/OQAM),使每个用户能够根据各自的信道条件选择合适的成形滤波器函数,进而满足多址接入系统达到全局最优化。
2 系统描述
现有研究表明,如果选择IOTA函数作为正交频分复用系统的成形滤波器,该函数仅满足实数域(real field orthogonality)正交条件的特性,使OFDM系统必须采用OQAM调制方式,则OFDM/OQAM发送信号可以表示为[10]

其中am,n表示第n个符号,第m个子载波发送的实数信号,v0和τ0代表OFDM/OQAM系统子载波间隔和发送信号时间间隔,g(t)表示成形滤波器函数即IOTA函数,如图1所示。由于OFDM/OQAM系统仅仅满足实数域严格正交条件,代替了传统CP-OFDM 系统中的复数域(Complex field orthogonality)正交条件,且实数域正交条件表示如下:

图1 OFDM/OQAM系统发送端结构框图

根据式(2),如果m=k且n=l,实数域正交条件为实数符号。如果不满足该条件,则为纯虚数符号。
3 OFDM/OQAM系统自适应波形设计
3.1 多载波系统成形滤波器优化理论
对于成形滤波器最优化设计而言,OFDM/OQAM 系统可以根据无线信道传输环境选择合适的成形滤波器,例如根据信道散射函数调制成形滤波器参数[4]。为了满足复杂信道条件下抑制 ISI和ICI的需求,OFDM/OQAM 系统发送端成形滤波器应满足[5]:

其中τ0和v0分别表示成形滤波器在时间域和频率域尺度,Δt和Δf分别表示无线传输信道的最大多径时延和最大频率偏移。根据式(3),为了满足OFDM/OQAM系统抑制ISI和ICI的效果,其时频聚焦区域应该完整包含无线信道散射函数,使基于该成形滤波器的OFDM/OQAM系统在该无线信道条件下具有最优化性能,如图2所示。
回顾IOTA函数,各向同性特性使其在时间域与频率域具有相同的衰减特征,即[6]

根据式(4),基于IOTA函数的OFDM/OQAM系统满足:

图2 正交频分复用系统成形滤波器时频优化设计准则

从式(5)可知,基于 IOTA函数的 OFDM/OQAM 系统当且仅当无线信道时间域和频率域的Δt和Δf满足式(5),能够取得最优性能。
在实际无线传输系统中,多径时延和频率偏移Δt和Δf随着时间和空间的变化而不断改变,比如在点对点通信情况下,无线通信信道呈现为多径衰落信道;当高速列车在开阔地与基站之间通信的情况下,无线通信信道呈现为多普勒频移信道。综上所述,基于IOTA函数的OFDM/OQAM系统并不能保证任何时刻都保持最优传输状态。
3.2 OFDM/OQAM系统自适应波形设计
为了抑制无线通信环境中的ISI和ICI,OFDM/OQAM 系统需要选择具有良好时频聚焦特性的成形滤波器达到上述目的。尽管Gauss函数具有良好的时频聚焦特性,但是该函数并不满足任何正交条件(包括复数域正交条件,实数域正交条件)。利用正交变换方式对Gauss函数进行正交化处理,则扩展高斯函数(Extended Gauss Function,EGF)表达式如下[3]:

其中gα表示Gauss函数,a表示EGF函数扩展因子。EGF函数不仅具有Gauss函数的时间频率聚焦特性,并且确保函数之间相互严格正交,如图3所示。
EGF函数的傅里叶变换表达式与函数本身具有相似的表达式:

其中F(*)表示傅里叶变换运算符。当a=1,τ0=v0=1 /2时,该函数的傅里叶变换等于其自身,即是IOTA函数。考虑到不同扩展因子,本文对基于EGF函数的 OFDM/OQAM 系统的模糊函数(ambiguity function)Ag(τ,v)进行分析,其中模糊函数定义为

模糊函数是关于时间和频率的2维函数,能够反映基于该函数的OFDM/OQAM系统的时频特性。首先证明EGF函数的扩展特性,其中Gauss函数的可以表示为

并且Gauss函数g(t)的时域扩展特性可以表示为

对于EGF函数系数序列dk,α,v0而言,该序列满足

结合式(6),式(10)和式(11)可推导出:

根据式(12),通过采样时间间隔Ts=2τ0/N和简单的数学推导和变量替换,基于 EGF函数的OFDM/OQAM系统模糊函数满足:

从上述公式可知,基于EGF函数的OFDM/OQAM系统通过调整扩展因子a能够改变系统的时频聚焦特性,仿真结果如图4所示。
根据图4,改变EGF函数中扩展因子a,时频聚焦特性也呈现出不同的特征:
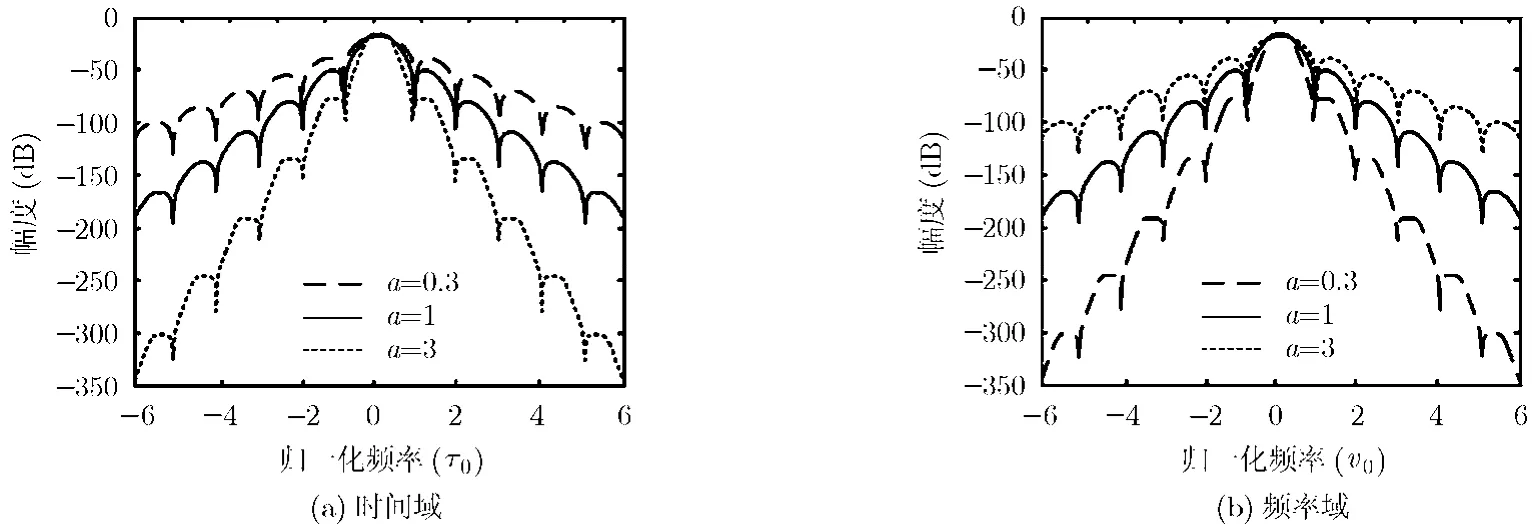
图3 EGF函数及傅里叶变换

图4 a=0 .3,3情况下,EGF函数模糊函数
(1)a<1,EGF函数随着时间偏移缓慢下降,具有良好的时间聚焦特性,能够有效地抑制ISI;
(2)a≈1,EGF函数等效于IOTA函数,时域与频域具有相同的聚焦特性;
(3)a>1,EGF函数随着频率偏移缓慢下降,具有良好的频率聚焦特性,能够有效地抑制ICI。
综上所述,根据正交频分复用系统最优化理论,针对不同的无线信道环境,基于EGF函数的OFDM/OQAM 系统选取不同的扩展因子参数,能够有效地优化不同应用场景下的系统性能。
3.3 基于成形滤波器函数的正交频分多址接入技术
基于传统 OFDM 技术的正交频分多址接入技术(Orthogonal Frequency Division Multiple Access,OFDMA)成为现在的主流的多址接入方式,例如LTE下行链路[11]。然而,传统OFDMA多址方式仍然存在CP-OFDM技术的固有缺陷,即子载波具有较高的带外辐射,导致:
(1)多普勒频移对传统 OFDMA 系统引入较强的子载波间干扰;
(2)传统 OFDMA 系统对相邻频带的无线传输系统引入较强的相邻信道干扰;
(3)OFDMA需要预留部分空子载波抑制相邻信道干扰,降低了系统的频谱利用率。
通过上述CP-OFDM与OFDM/OQAM系统性能对比,由于成形滤波器的时频聚焦特性以及可调性,OFDM/OQAM系统具有可调的带外滚降特性,更高的频谱利用率和对ISI和ICI的稳健性。如果把OFDM/OQAM技术扩展至正交频分多址接入系统,则能够构建基于成形滤波器函数的正交频分多址接入方式(OFDMA/Offset QAM,OFDMA/OQAM)。
在基于EGF函数的OFDMA/OQAM多址接入系统中,不同用户根据各自的无线传输信道条件,调整 EGF函数扩展因子a改变无线传输链路的时频聚焦特性,进而有效地提高单个用户的传输性能,最终提高OFDMA/OQAM多址接入系统容量,因此基于EGF函数的OFDMA/OQAM系统发送端与接收端如图5和图6所示。
基于EGF函数的OFDMA/OQAM多址接入技术表现为:
(1)具有较高的时间弥散性:如果多址接入系统中某个用户与基站之间的无线传输信道具有较高的时间扩展性,选取具有良好时间聚焦特性的EGF函数(a<1),则该用户与基站间的传输链路能够有效地抑制ISI;

图5 基于EGF函数的OFDMA/OQAM系统链路发送端框图
(2)具有相同或者相近的时间/频率扩展性:如果多址系统中某个用户与基站之间的无线传输信道具有相同或者相近的时间/频率扩展性,选取具有等效时间/频率聚焦特性的EGF函数(a=1,即IOTA函数),则该用户与基站间的传输链路能够有效地抑制ISI和ICI;
(3)具有较高的频率扩展性:如果多址系统中某个用户与基站之间的无线传输信道具有较高的频率扩展性,选取具有良好频率聚焦特性的 EGF函数(a>1),则该用户与基站间的传输链路能够有效地抑制ICI。

图6 基于EGF函数的OFDMA/OQAM系统链路接收端框图
4 仿真分析
为了综合比较基于 EGF函数的 OFDMA/OQAM与传统CP-OFDMA多址接入系统,本文对两种典型的信道环境[12]进行仿真研究:(1)扩展车用A信道模型 (Extended Vehicular A Model,EVA),(2)高速列车信道环境(High Speed Train Scenario)。系统参数如表1所示。

表1 OFDMA/OQAM与CP-OFDMA系统仿真参数
(1)EVA信道下系统性能 根据EVA信道参数可知,该信道具有较小的多普勒频移但是具有严重的多径分量,即该信道条件下具有很强的ISI,较弱的ICI。基于EGF函数的OFDM/OQAM系统在EVA信道情况下系统仿真结果如图7所示。当扩展因子a不断减小时,基于 EGF函数的 OFDM/OQAM系统的时间聚焦性不断增强,且能够有效地抵抗 EVA信道情况下的多径干扰。此外,由于OFDM/OQAM系统不需要添加CP用于消除多径干扰的影响,在相同的Eb/N0情况下,OFDM/OQAM系统的性能优于CP-OFDM系统。
(2)高速列车情况下系统仿真 在高速列车情况下 (120 km/h和350 km/h),其对应的多普勒频移分别为267 Hz和778 Hz (2.4 GHz载频)。该仿真结果主要针对开阔地基站与移动设备之间的信道条件,即存在很强的视距路径,因此无线传输信道建模为单径莱斯信道(K≫1),仿真结果如图8所示。通过对比扩展因子a=0 .3,1,3的情况,随着扩展因子a不断增加,SER性能不断提高。在 120 km/h情况下,在 S ER=3× 1 0-3处,OFDM/OQAM系统 (a=3)的SER性能比a=1和a=0.3条件下分别获取了1.8 dB和4 dB性能增益。在350 km/h情况下,在 S ER=2× 1 0-2处,OFDM/OQAM系统(a=3)的性能相对a=1的性能获取了2 dB性能增益。
对比CP-OFDM系统,基于EGF函数的OFDM/OQAM系统有明显的性能提升。在120 km/h情况下,在 S ER=1 0-2处,OFDM/OQAM系统(a=3)的SER性能比CP-OFDM系统获取了2.2 dB性能增益;在 350 km/h情况下,在SER=4 × 1 0-2处,OFDM/OQAM 系统 (a=3)的 SER性能比CP-OFDM系统获取6.2 dB性能增益。这是因为,CP-OFDM系统对子载波间干扰非常敏感,高速列车运动产生的多普勒频移使CP-OFDM系统性能急剧恶化。然而,基于 EGF函数的 OFDM/OQAM 系统利用函数的时频聚焦性有效地抑制了多普勒频移,因此OFDM/OQAM系统在高速列车情况下比CP-OFDM系统SER性能有明显的提升。
5 结束语
本文根据正交频分复用系统设计优化理论,基于EGF函数的OFDM/OQAM系统通过调节成形滤波器函数的扩展因子,改变基于该函数的OFDM/OQAM系统的时频聚焦性,进而匹配无线传输信道的散射函数,获取最佳的传输性能。此外,针对现有基于CP-OFDM技术的多址接入系统,本文将OFDM/OQAM技术扩展至正交频分多址接入系统,构建基于EGF函数的正交频分多址接入方式(OFDMA/OQAM),使每个用户能够根据各自的信道条件选择合适的EGF函数扩展因子,使OFDMA/OQAM多址接入系统达到全局最优化。

图7 EVA信道,OFDM/OQAM系统的SER与 E b /N0的关系
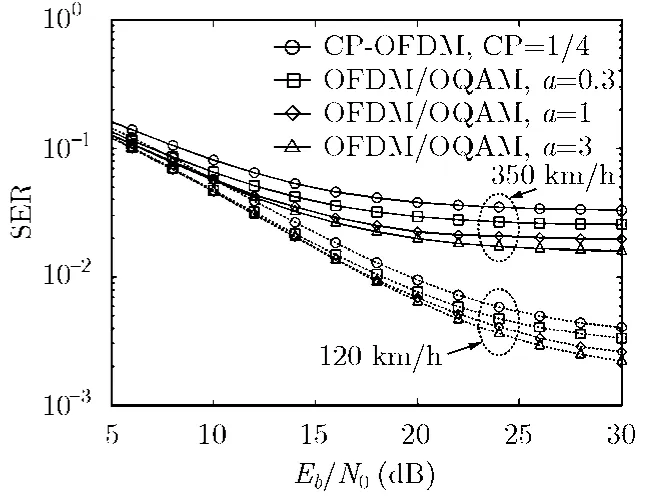
图8 高速列车120 km/h和350 km/h,OFDM/OQAM系统SER与 E b /N 0的关系
[1]LeFloch B,Alard M,and Berrou C.Coded orthogonal frequency division multiplex[J].Proceedings of the IEEE,1995,83(6): 982-996.
[2]Strohmer T and Beaver S.Optimal OFDM design for timefrequency dispersive channels[J].IEEE Transactions on Communication,2003,51(7): 1111-1122.
[3]Bölcskei H,Duhamel P,and Hleiss R.Orthogonalization of OFDM/OQAM pulse shaping filters using the discrete Zak transform[J].Signal Processing,2003,83(7): 1379-1391.
[4]Kozek W and Molisch A F.Nonorthogonal pulseshapes for multicarrier communications in doubly dispersive channels[J].IEEE Journal on Selected Areas in Communications,1998,16(8): 1579-1589.
[5]Schniter P.On the design of non-(bi)orthogonal pulse-shaped FDM for doubly-dispersive channels[C].IEEE International Conference on Acoustics,Speech,and Signal Processing,Quebec,Canada,2004,3: 817-820.
[6]Bellanger M,Renfors M,and Ihalainen T.OFDM and FBMC transmission techniques: a compatible high performance proposal for broadband power line communications[C].IEEE International Symposium on Power Line Communications and Its Applications,Rio de Janeiro,March 2010: 154-159.
[7]Gao X Q,Wang W,Xia X G,et al..Cyclic prefixed OQAM-OFDM and its application to single-carrier FDMA[J].IEEE Transactions on Communications,2011,59(5):1467-1480.
[8]Katselis D,Kofidis E,Rontogiannis A,et al..Preamble-based channel estimation for CP-OFDM and OFDM/OQAM systems: a comparative study[J].IEEE Transactions on Signal Processing,2010,58(5): 2911-2916.
[9]Bellec M and Pirat P.OQAM performances and complexity[C].IEEE P802.22 Wireless Regional Area Network (WRAN),Jan.2006.http://www.ieee802.org/22/Meeting documents/2006 Jan/ 22-06-0018-01.
[10]Du J and Signell S.Classic OFDM systems and pulse shaping OFDM/OQAM systems.http://www.wireless.kth.se/projects/NGFDM/publication_files/NGFDM_report07022 8.pdf,2007.2.
[11]An Introduction to LTE.3GPP LTE Encyclopedia.Retrieved,2010-12-03.
[12]The 3rd Generation Partnership Project Technical Specification Group Radio Access Network Evolved Universal Terrestrial Radio Access (E-UTRA)Base Station (BS)Radio Transmission and Reception (Release 8),3GPP TR 36.804 V1.2.0,2008.

