基于邻域均方连续差分的SAR图像边缘提取算法
傅兴玉 尤红建 付 琨
①(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)
②(中国科学院电子学研究所 北京 100190)
③(中国科学院研究生院 北京 100049)
1 引言
由于SAR图像乘性斑点噪声的影响,传统基于梯度的边缘检测算子不具有恒定虚警率的特性,难以确定边缘的准确位置,检测效果不理想[1]。为此,文献[2]提出了基于ROA (Ratio Of Average)的SAR图像边缘算子以克服基于梯度的边缘算子对乘性噪声敏感的缺点。之后陆续出现了许多以ROA为基础的SAR图像边缘检测算子,比如MROA(Modified Ratio Of Averages),RGOA(Ratio and Gradient Of Averages),ROEWA(Ratio Of Exponentially Weighted Averages)[3]。文献[4]提出了一种基于最佳似然函数的SAR图像边缘检测算法,并提出基于FWSE(Fixed Window Scanning Edge)或SWCE (Scanning Window Central Edge)的窗口分析提高边缘定位精确度。文献[5]利用改进的ROEWA算法,在计算边缘强度的同时,利用二次曲线进行估计边缘方向。
基于ROA的SAR图像边缘算子,利用4个方向两侧均值最小比值作为边缘强度,对SAR图像斑点噪声具有一定的抑制能力,但没有充分考虑到像素周围均值分布和边缘走向,对噪声的抑制能力有限。本文提出了一种基于邻域均值连续差分平方和的边缘算子,以提高SAR图像边缘检测性能。首先,将滑动窗口分成多个互不重叠的子区域,采用邻域均值连续差分平方和作为像素的边缘强度,并采用分区均值差别最大的方法估计边缘走向。然后,根据边缘走向对边缘强度图像进行细化,消除真实边缘附近的虚假边缘,并采用基于平均强度变化率的自适应双阈值连接算法提取边缘。仿真和实测SAR图像实验结果表明,本文边缘算子在不同亮度的同质区域表现出恒定虚警率的特性,具有较高的检测率和边缘定位精度,提取得到的边缘线段的连续性保持也较好。
2 基于邻域均方连续差分的边缘算子
基于邻域均值连续差分平方和(均方连续差分)的边缘算子分析如下:对大小为N×N的滑动窗口,首先将其分割成多个互不重叠的等面积子区域,然后计算各子区域像素均值,并对均值连续求差,以连续差值平方和作为中心像素的边缘强度,如式(1)所示。

其中n表示邻域分块的个数,μi,μj分别表示标号为i和j分块的均值,mod表示求余操作。图1给出了将9×9的滑动窗口划分成8个邻域分块的示意图。
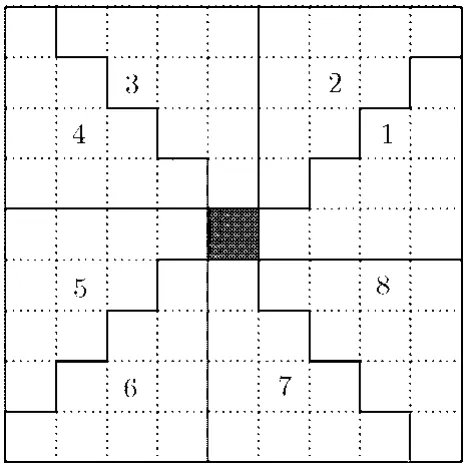
图1 邻域分区示意图 (分块数量n=8)
本文边缘算子统计像素点周围邻域均值的分布特性来计算边缘强度,通过检验邻域均值是否一致来判断窗口中心像素是处在同质区域内部还是区域边界。对于每个邻域子区域,本文假定其满足同质性要求,根据中心极限定理,若干同分布的独立随机变量之和渐进正态分布,则有

其中X表示SAR图像像素值对应的随机变量,E表示X的数学期望,D表示其方差,m表示样本数量,对应子分区内的像素数目,μi表示标号i分块的均值。
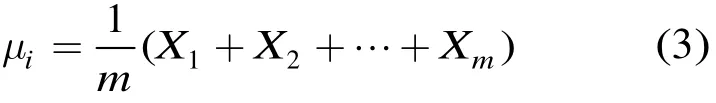
设ξ=E(X),σ2=D(X),则有

如果像素点处在同质区域内部,则邻域分块均值具有相同正态分布,同时邻域分块互不重叠,均值互相独立。由正态分布的可加性可知
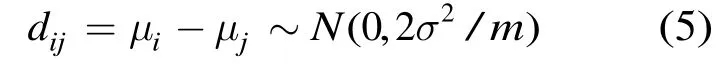
则有


因此,通过正交变换可以将式(1)中的边缘强度转换成n个互相独立的随机变量之和[6]。由 Fisher定理可知,独立同分布的N(0,σ2)变量的线性组合仍服从零均值的正态分布,并且互相统计独立。因此,式(1)中边缘强度满足自由度为n的卡方分布,其分布密度函数如式(8)所示

其中Γ表示 Gamma函数,σ表示区域方差,n表示邻域分块数量,NL表示滑动窗口的像素数量。
如果像素点处在区域边界上,则邻域分块可以分成两类,分别记为类别I和类别II,每个类别内部的邻域分块具有相同的分布。因此,式(1)中的边缘强度由以下3部分组成,类别I内部的均方差,类别II内部的均方差,以及类别I和类别II之间的均方差。对于类别I和类别II内部的均方差,其形式与同质区域类似,下面着重讨论类别之间的均方差。
设类别I和类别II分布的均值分别为ξI,ξII,方差分别为,则类别I和类别II之间的均值差服从下述分布,并且互相统计独立。
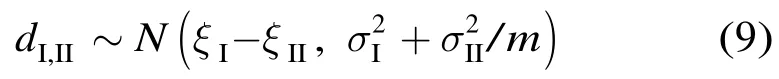

由

综上,在同质区域内部,本文提出的边缘算子与区域亮度无关,表现出恒定虚警率的特性,而在边界处强度值与均值差平方有关,具有较大响应。
3 边缘方向估计及细化
边缘走向是边缘一个重要量度,对后续边缘细化和边缘连接起着重要的作用。与传统使用梯度变化最小的方向作为边缘走向[7,8]不同的是,本文提出一种基于类间均值差别最大的边缘方向估计方法,如图2所示。给定两个方向,将邻域子块分成两组,分别统计两组均值的算术平均值,使用均值差别最大的方向组合作为像素点的边缘方向。对于图1的窗口划分方式,则共有28种可能的方向组合,图2给出部分边缘走向示意图。
由于滑动窗口的影响,单边缘像素点会产生响应多次,产生边缘展宽效应,一般借助边缘细化算法对边缘强度图进行细化。ROA算子仅能估计4种不同边缘走向,当实际走向与窗口划分方向不一致时,会导致真实边缘点被消除,造成边缘线段断裂。与传统ROA算子不同的是,本文方法可以更好地估计出真实边缘点走向,较好地在保留真实边缘的同时,消除真实边缘附近的虚假边缘。
对于图像上的每个像素点(x,y),记其边缘强度值为s(x,y),边缘方向记为(dir1,dir2),然后沿着边缘走向中心线方向比较边缘强度值,搜索距离为d,如图3所示。记搜索路径上的像素点(x',y')的强度值为s(x',y'),如果s(x,y)不小于搜索路径上的任一点的强度s(x',y'),则认为该像素点是局部极大值点,予以保留。否则认为点(x,y)不是局部极值点,予以消除。搜索距离d是一个尺度参数,一般取窗口大小N的1/2。
如果点(x',y')正好落在像素点上,s(x',y')等于相应像素点的边缘强度值。否则,采用双线性插值计算点s(x',y')的边缘强度值,如图3(d)的情况所示。
由于SAR图像受斑点噪声影响严重,在灰度变化缓和的边界处,真实边缘点在细化过程中可能被错误地消除,导致边缘不连续。通过实验发现,边缘断续主要是由于像素点的估计方向与实际方向不一致产生的,本文采用下述方法对抑制路径方向进行修正。

图2 像素点不同边缘方向示意图
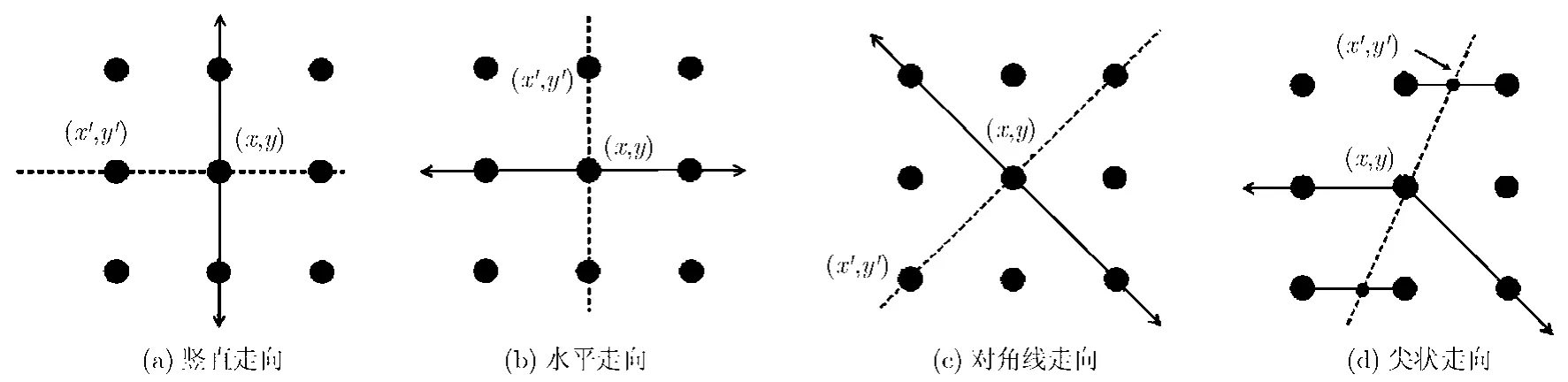
图3 不同方向组合下边缘细化示意图 (箭头表示估计的边缘方向,虚线表示边缘细化路径)
对于每个像素点,在非极大值抑制过程中,如果发现抑制路径上已经存在多个被标记的边缘像素点,则认为当前像素点边缘方向与实际不一致,应予以修正。将中心线方向作为像素点的修正走向,并沿着中心线的垂直方向进行非极大值抑制,修正示意图如图4所示。
4 自适应双阈值连接处理
通过边缘细化处理,消除了真实边缘附近的虚假边缘,但细化结果中存在部分漏检边缘像素,导致边缘线段不连续,本文采用一种自适应双阈值连接算法连接断裂的边缘线段,提高边缘的完整性。传统Canny算子进行边缘连接时,需要确定高,低阈值参数,不同的阈值对边缘检测的结果影响很大[9]。同一图像尤其是SAR图像中,不同边缘取得最佳边缘检测效果的阈值各不相同,如果采用固定阈值则会检测出虚假边缘或丢失局部边缘。本文采用基于平均强度的方法对上述方法进行改进,算法的主要步骤如下:
首先,确定高阈值系数Rhigh,其定义为边缘强度值不小于阈值的像素点所占总像素的比例

其中f(x)表示边缘强度的概率分布密度函数,Thigh表示高阈值,通过边缘强度的累计分布函数和高阈值系数可求出该值。将边缘强度不小于Thigh的像素定义为强边缘点,并标记为种子点。
其次,设定边缘线段平均强度最大变化率Δmax,其值为0到1之间的小数。然后从种子点出发进行边缘连接。以连接点八邻域内未连接像素中强度变化最小的像素作为下一个连接点。如果下一连接点为种子点或者平均强度的变化率不大于Δmax,连接该点,并更新边缘线段的平均强度,继续跟踪。如果在八邻域内找不到满足条件的边缘像素点,结束跟踪。边缘线段平均强度的变化率计算公式如式(13)所示

其中k和μk分别表示连接前边缘线段的像素数目和平均强度,s表示下一连接像素点的边缘强度值。
最后,按照线段长度,平均强度等条件对提取结果进行过滤,消除长度较小或者孤立的边缘像素。
上述自适应双阈值连接算法中使用了两个比例参数,高阈值系数Rhigh和平均强度最大变化率Δmax。Rhigh用来控制边缘连接的种子点数目,在进行边缘连接之前已进行了边缘细化处理,真实边缘附近的虚假边缘像素已被较好地消除,在细化后的图像中,真实边缘所占比例较大,因此高阈值系数一般取值较大,例如0.7~0.9即可达到较好的效果。Δmax用来动态确定边缘连接过程中弱边缘连接阈值,对于不同的边缘线段或者同一线段连接不同阶段,弱边缘连接与否的阈值不尽相同,实现了根据边缘线段的平均强度进行自适应的阈值处理。其值一般根据弱边缘的保留程度进行设定,在实际中可设定为低阈值与高阈值的比例因子,一般取0.5即可。
5 实验结果与分析
5.1 边缘检测性能评估
优秀SAR图像边缘算子,一方面在真实边缘处取得极大响应,并尽可能地消除虚警边缘,具有较高的检测率,另一方面检测边缘距离真实边缘尽可能近,具有较高的定位精度。文献[10]给出了边缘算子检测率的评估准则,
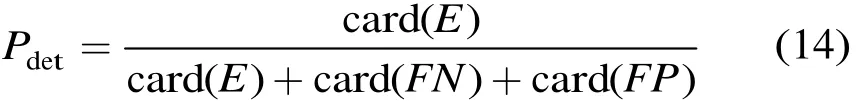
其中E为检测结果和真实边缘集合的交集,FN为漏检集合,定义为未检测到的真实边缘像素集合,FP为误检集合,定义为实际为背景像素点,却误检为边缘像素点的集合。card表示集合的元素数目。Pdet是处在0到1之间的小数,如果真实边缘都被正确检测,同时没有背景像素点被误检为边缘点,则有Pdet=1。Pdet越接近0,说明有更多的真实边缘点被漏检或者背景像素点被误检为边缘点。
对于每个真实边缘点,标记检测集合中与其距离最近的边缘点作为该点的检测结果,并计算两者的位置偏差d。设定距离阈值D。集合E为真实边缘集合中距离偏差较小(d≤D)的边缘集合;FN为真实边缘中实际位置与检测位置偏差较大(d>D)的边缘像素集合;FP为不存在真实边缘与其对应的检测边缘集合。
边缘算子得到的边缘应该尽可能接近实际边缘点的位置。为了评价算子的边缘定位精度,本文对于真实边缘像素点,计算其实际位置(xtrue,yt
rue)和检测位置(xdet,ydet)的偏差,以正确检测集合E中的所有边缘点的平均偏差作为边缘定位精度的评价准则。
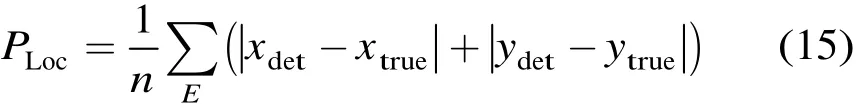
其中n表示集合E中的像素数目。PLoc是大于零的实数,其值越接近零,说明算子的边缘定位精度越好;反之定位精度越差。
5.2 仿真SAR图像边缘提取实验
选用仿真测试SAR图像进行实验,仿真图像如图5(a)所示。分别采用Canny算子,4方向ROA算子和本文算子对仿真SAR图像进行处理,得到图像的梯度图或边缘强度图像,分别如图5(b),5(c)和5(d)所示。ROA算子和本文算子的滑动窗口大小均为9×9。
通过对比可以发现,与Canny算子相比,ROA算子和本文算子得到的边缘强度与区域亮度无关,在高低亮度同质纹理区域内部的响应都比较小,而在边界处具有局部极大响应。图6给出了 4方向ROA算子和本文算子在低亮度同质区域,高亮度同质区域以及边界上的边缘强度分布直方图。不难看出,本文算子的边缘强度要明显优于 4方向 ROA算子,前者得到的边缘强度分布曲线较为平滑,波动较小,表明对斑点噪声的抑制能力较好。由于滑动窗口的影响,本文算子和 ROA算子得到的边缘响应较宽,借助细化算法可消除真实边缘附近的虚假边缘,确定边缘的准确位置。
图8(a)和 8(b)分别给出了使用 Canny算子和ROA算子进行边缘检测的结果图像。其中,Canny算子使用的参数如下:高斯平滑窗口噪声标准差为0.55, 高阈值为380,低阈值为190。对于ROA算子,以取得最小比值的窗口划分方向作为边缘走向(如图7所示),并沿着与走向垂直的方向进行细化,最后采用本文自适应双阈值连接算法对细化结果进行连接,高阈值系数Rhigh=0.82,最大平均强度变化率Δmax=0.5,最后得到ROA边缘检测结果如图8(b)所示。

图5 不同梯度算子实验结果对比图

图6 ROA算子和本文算子在不同类型区域的分布直方图

图7 ROA算子边缘走向示意图 (中间白色线框表示边缘走向,虚线表示边缘细化方向)

图8 仿真SAR图像边缘提取实验
图8(c)是采用本文边缘细化算子对得到的边缘强度图像进行细化的结果,抑制距离为5像素。图8(d)进行自适应双阈值连接处理后的结果图像,使用参数与上述 ROA后处理中相同。对比提取结果不难看出,Canny算子得到边缘结果中在高灰度同质区域边界附近存在较多的误检情况,而 ROA算子和本文算子的检测结果较为理想,误检和漏检较少。相比之下,本文方法得到区域边缘比 ROA算子更平滑,边缘完整性保持较好,说明本文算子对SAR图像斑点噪声抑制能力较好。同时本文算子对拐点处的边缘提取效果较好。
5.3 实测SAR图像实验结果
实验1 选用一幅实测机场跑道SAR图像进行边缘提取实验,原始SAR图像如图9(a)所示,提取的主要目的是得到SAR图像中跑道的轮廓。图9(b)是手工勾绘的边缘结果,用来对边缘提取结果进行性能评估。分别利用 Canny,ROA和本文算子对SAR图像中的边缘进行提取,结果分别如图9(c),9(d)和 9(e)所示。Canny算子高斯平滑窗口同 4.2节中仿真图像实验相同,高低梯度阈值分别为 240和120。ROA算子和本文算子使用的滑动窗口大小均为9×9,后处理过程中的边缘细化抑制长度为5像素,自适应双阈值边缘连接中高阈值系数Rhigh=0.80,平均强度最大变化率Δmax=0.5。从结果图像不难看出,Canny算子得到边缘存在较为严重的断裂和毛刺现象,跑道边界提取不完整。ROA算子和本文算子的提取效果较为理想,跑道轮廓提取相对完整。相比之下,ROA算子在跑道轮廓拐角处的提取效果不理想,部分边界像素点漏检,导致边缘断裂,而在这些地方本文算子提取效果较好,提取的边缘具有较好的连续性。由于滑动窗口的影响,ROA算子和本文算子对SAR图像中的细线结构检测效果均不理想。

图9 实测机场跑道SAR图像边缘提取实验
实验2 选用一幅实测海域高分辨率SAR图像进行边缘提取。原始SAR图像如图10(a)所示,图像左下角为海水区域,右上角为陆地部分,包括机场跑道和建筑物等。图10(b)是手工勾绘的边缘结果图像,图10(c),10(d)和10(e)分别是Canny,ROA和本文算子的边缘提取结果图像,3种算子的实验参数与实验1相同。不难看出,Canny算子边缘提取结果中,海岸线部分边缘和其上侧的整条边界漏检,同时高亮度建筑区域存在严重的误检情况。而ROA算子提取结果中,同质区域内部存在噪声形成的虚警边缘,说明对斑点噪声的抑制能力不强,同时边缘断裂严重,提取结果不理想。虽然本文算子在缓变的边缘存在漏检情况,但总体的检测效果要明显优于Canny算子和ROA算子,海岸线,跑道等强边缘以及位于海岸线上侧的弱边缘保持完整,同时在亮度较低的海水纹理区域和亮度较高的建筑物纹理区域,较好地抑制了斑点噪声形成的虚警边缘,误检率较低。
表1给出了上述3种边缘检测算子性能评估对比结果,其中用来评估边缘检测性能和定位精度的最近真实边缘距离阈值D=5像素。从表中结果可以看出,本文算子和ROA算子对SAR图像边缘的检测性能明显优于Canny算子,说明Canny算子在SAR图像上具有较多误检或者漏检,在边缘定位精度上两者也略优于Canny算子。相比之下,本文算子比 ROA算子具有更好的检测率和更高的边缘定位精度。从得到的边缘线段的数目和平均长度的结果可以看出,本文算子得到的数目最少,平常长度最长,说明本文算子提取得到的边缘线段的连续性较好,而ROA算子和Canny算子边缘断裂较多,连续性保持较差。在运算时间上,由于本文算子和ROA算子都需要统计滑动窗口内的像素值,运算时间主要花费在边缘强度计算和边缘方向估计,运算时间要明显长于Canny算子,在后处理阶段,运算时间主要与提取边缘线段数目和长度有关。本文算子提取的边缘线段连续性保持最好,线段数目较少,运算较快。相比之下,本文算子边缘强度估计运算时间明显少于ROA算子。

图10 实测海域SAR图像边缘提取实验
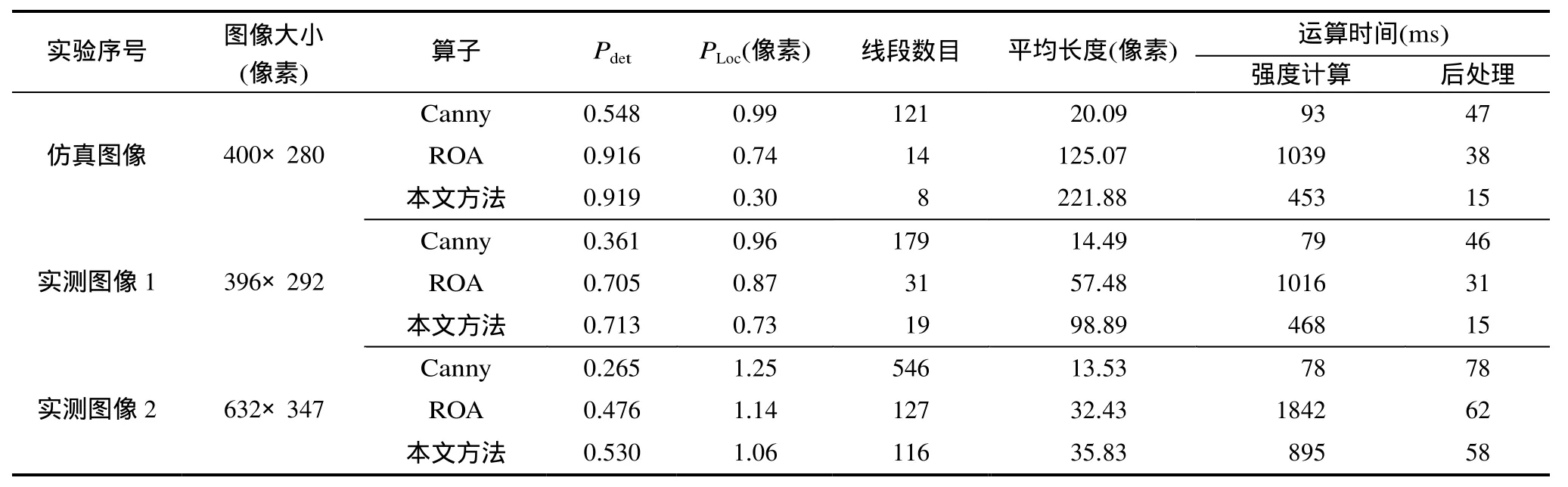
表1 3种边缘算子评估对比表
6 结束语
通过以上 3组实验对比分析不难发现,对于SAR图像边缘检测来说,传统基于梯度的 Canny算子,在梯度较大的强边缘处具有较好的检测效果,但对于两侧亮度值差别较小的边缘点漏检率较高,同时不具有恒虚警性,在高亮度同质区域内部误检率较高,对斑点噪声抑制能力差。基于ROA的边缘检测算子,沿着4个不同的方向将窗口分成互不相交的两部分,计算两部分均值比,以4个方向最小比值作为边缘强度,该算子与区域均值无关,具有恒定虚警率的特性,但没有充分考虑像素点邻域像素值分布,对斑点噪声的抑制能力不强,同时对边缘走向估计有限,造成较多的边缘断裂。本文提出的基于邻域均方连续差分的边缘算子从像素邻域均值分布特性出发,以邻域均值连续差分平方和作为边缘强度,边缘强度衡量因子与区域亮度无关,表现出恒定虚警率的特性,同时可以较好地确定边缘方向,并结合边缘细化和自适应双阈值连接处理,较好地提取得到SAR图像中边缘。通过仿真和实测SAR图像实验对比发现,本文提出的边缘算子可以较好地提取SAR图像中的边缘,检测率和边缘定位精度较好,同时边缘线段的连续性保持较好。下一步将研究多边缘模型和多尺度方法来对本文方法进行改进,达到更好的SAR图像边缘检测性能[11,12]。
[1]安成锦,杜琳琳,王卫华,等.基于融合边缘检测的SAR图像线性特征提取算法[J].电子与信息学报,2009,31(6):1279-1282.An Cheng-jin,Du Lin-lin,Wang Wei-hua,et al..Linear feature extraction for SAR image based on fused edge detector[J].Journal of Electronics&Information Technology,2009,31(6): 1279-1282.
[2]Touzi R,Lopbs A,and Bousquet P.A statistical and geometrical edge detector for SAR images[J].IEEE Transactions on Geosciences and Remote Sensing,1988,26(6): 764-773.
[3]Fjortoft R,Marthon P,Lopes A,et al..Multiedge detection in SAR images[C].IEEE International Conference on Acoustics,Speech and Signal Processing,Munich,Germany,April 1997,Vol.4: 2761-2764.
[4]Oliver C J,Blacknell D,and White R G.Optimum edge detection in SAR[J].IEE Proceedings Radar,Sonar&Navigation,1996,143(1): 31-40.
[5]陈天泽,吴俞昊,李燕.基于DS理论的高分辨率SAR图像复制背景直线边缘提取方法[J].信号处理,2011,27(1): 94-101.Chen Tian-ze,Wu Yu-hao,and Li Yan.The linear edge extraction with complicated background in high resolution SAR images based on the DS evidence theory[J].Signal Processing,2011,27(1): 94-101.
[6]李庆海,陶本藻.概率统计原理和在测量中的应用(修订本)[M].北京: 测绘出版社,1990: 185-186.Li Qing-hai and Tao Ben-zao.Principles of Probability Statistics and Its Application to Surveying (2nd Ed.)[M].Beijing: surveying and Cartography Press,1990: 185-186.
[7]Papari G and Petkov N.Edge and line oriented contour detection: State of the art[J].Image and Vision Computing,2011,29(2): 79-103.
[8]Zhou G Y,Cui Y,Chen Y L,et al..SAR image edge detection using curvelet transform and Duda operator[J].Electronics Letters,2010,46(2): 167-169.
[9]Sen D and Pal S K.Thresholding for edge detection in SAR images[C].International Conference on Signal Processing,Communications and Networking,Chennai,Jan.2008:311-316.
[10]杨朝辉,陈鹰.基于ROC融合准则的SAR边缘检测算法[J].光电子·激光,2010,21(7): 1053-1057.Yang Chao-hui and Chen Ying.Edge detection algorithm of SAR images based on ROC fusion rule[J].Journal of Optoelectronics·Laser,2010,21(7): 1053-1057.
[11]Dachasilaruk S.Multiscale edge detection for SAR image de-speckling[C].5th International Conference on Visual Information Engineering,Xi,an,China,July 2008: 582-587.
[12]钟钒,周激流,郎方年,等.边缘检测滤波尺度自适应选择算法[J].自动化学报,2007,33(8): 867-870.Zhong Fan,Zhou Ji-liu,Lang Fang-nian,et al..Adaptive scale filtering for edge detection[J].Acta Automatica Sinica,2007,33(8): 867-870.

