利用自动识别系统信息进行高频地波雷达天线阵校正

田文龙 李高鹏 许荣庆

(哈尔滨工业大学电子工程技术研究所 哈尔滨 150001)

1 引言

高频地波雷达(HFSWR)利用沿海面传播的高频波段垂直极化电磁波探测海面舰船目标以及低空飞行目标。高频地波雷达使用天线阵接收目标回波信号，由于天线阵阵元老化、互耦、信号电缆长度不一致、天线制造误差等原因，天线阵不可避免地存在相位和幅度误差。这些误差将影响目标方位角估计精度，因此需要通过天线阵校正予以消除。现有的高频地波雷达天线阵校正方法主要分为两类，一类是使用专用校正目标(信标机)，即合作目标的校正方法，合作目标装有定位设备(如 GPS)并沿指定路线航行，文献[1-3]中给出了典型的例子。由于合作目标的真实方位已知，这类方法可以达到很高的阵列校正精度，但每一次实施校正时都必须部署相应的专用校正目标，因此成本较高，且难以实现随时校正。另一类方法是使用非合作目标的盲校正方法，这类方法使用方位未知的目标回波作为校正信号，例如视距内大型舰船目标、流星尾迹[4-6]等，利用目标回波信号对目标方位角和阵列误差同时进行估计，文献[7-9]给出了这类算法的典型例子。这类方法无需部署专用信标机等合作目标，因此成本较低，且可以做到随时校正，但是由于目标的方位未知并需要进行估计，将不可避免地产生目标方位角估计误差，从而影响校正精度，此外，这类方法通常需要使用多次迭代的方法计算目标方位和阵列误差的最大似然估计，因此计算量高于使用合作目标的校正方法。

针对上述两类校正方法的不足，本文中提出使用自动识别系统(Automatic Identification System,AIS)信息进行高频地波雷达天线阵校正。国际海事组织(IMO)规定，在国际水域航行的，毛吨位大于等于300 t的船舶，以及所有的客运船舶(不论大小)均必须安装A类AIS设备，目前全世界至少有40000艘船舶安装了A类AIS设备。该系统使用VHF收发装置，将目标自身的身份(各用户独一无二的身份编号)、位置(经纬度)、航速、航向、航行状态(机动自力航行、锚定、拖拽航行等)等信息以短信息的方式进行广播。处于该AIS收发机有效范围内的其他AIS用户，可以通过该信息来获取发射方的详细情况。AIS系统目前最主要的作用是 “防撞”，相对于船用雷达设备，AIS系统具有廉价和高精度的优势，AIS系统通常与船用GPS设备直接交联，其所报告的位置是船用GPS设备的测量值，因此具有GPS精度，其位置、航速、航向精度远高于一般搜索雷达[10]。AIS设备在水平方向上的可靠作用距离在74 km 左右，最远可达数百公里，因此近距离内的(尤其是100 km内的)、装有AIS设备的船只将同时被高频地波雷达和AIS系统捕获和跟踪。这些目标的真实位置可以通过AIS信息获得，因而可以作为“合作”目标用于高频地波雷达天线阵校正，使用这一范围内的大信噪比目标回波进行天线阵校正，可以得到与使用专用目标(如信标机)相似的精度，而无需专门部署相应的信标机，从而节约了校正成本，且可以做到随时校正。

2 高频地波雷达数据与AIS数据的同步与匹配

欲实现利用AIS数据对高频地波雷达天线阵实施校正，首要问题是实现雷达数据与AIS数据的同步和匹配。

由于工作原理不同，高频地波雷达与AIS系统具有不同的数据率。首先需要解决的问题是数据的同步。高频地波雷达的数据率是其相参积累周期(CIT)的倒数，在探测海面舰船目标时，高频地波雷达的相参积累周期通常在150 s以上；而AIS系统的数据率是可变的，对于以正常速度航行的大中型舰船，其定位信息的发送间隔在2-10 s左右。因此，由高频地波雷达提供的一个批次的目标数据无法保证与AIS系统提供的定位信息在时间上精确对准，如图1所示。从图1中可以看到，由于高频地波雷达与AIS系统具有不同的数据率，在时间轴上位于t2时刻的高频地波雷达数据无法在时间上与目标的AIS数据(t1＜t2＜t3)精确对准。为通过AIS数据得到目标在t2时刻的精确位置，使用线性插值的方法利用t1,t3时刻的AIS数据内推出目标在t2时刻的位置信息。设由AIS数据得到的目标在t1,t3时刻的位置坐标分别为 (x1,y1),(x3,y3)，而目标在t2时刻的位置为 (x2,y2)，则有

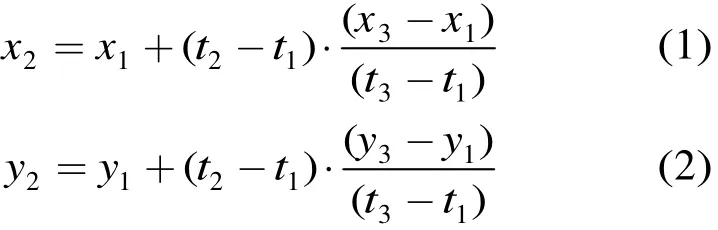
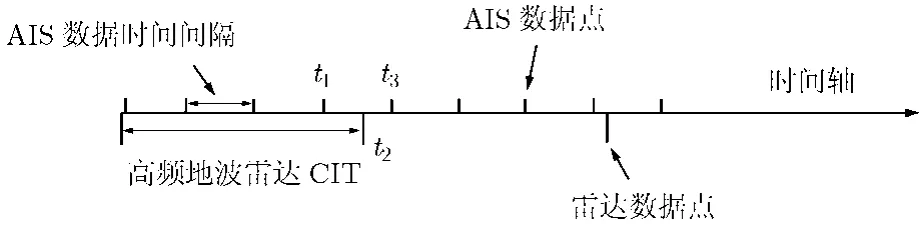
图1 高频地波雷达与AIS系统的数据率示意图

通过式(1)，式(2)即可实现 AIS定位信息与高频地波雷达数据在时间上的同步。对校正时段内所截获的所有AIS信息进行上述处理，即可得到AIS系统覆盖范围内所有目标在t2时刻的位置信息。用相同的方法处理AIS信息中的航速、航向等信息，即可得到t2时刻的目标航速、航向信息。

实现数据时间同步后，即可开始选择用于天线阵校正的海面目标，并获取其所对应的AIS数据。该数据匹配过程分3步完成。

(1)对雷达输出信号的距离-多普勒谱(距离-径向速度谱)实施筛选，选取大信噪比目标，要求目标的信噪比大于 30 dB，其筛选过程与门限检测完全一致。同时，所选择的目标的距离应在80 km以内，以确保其能被AIS系统可靠覆盖[10]。

(2)对上述筛选得到的大信噪比目标再次进行筛选，选择距离-多普勒谱上孤立的大信噪比目标，保证所选目标附近的几个距离门和多普勒门中均不存在其它目标。经过此次筛选所得到的目标，将是距离-多普勒谱上孤立的峰值。

(3)在 AIS数据集中搜索对应的数据点。使用AIS数据与雷达阵地的位置，可以计算出当前时刻AIS系统覆盖范围内的各个目标相对于雷达的距离(地球球大圆距离)和径向速度。AIS系统所发送的信息中，目标的位置信息使用经纬度表示。为得到高精度的距离估计结果，本文中采用 GRS80系统[11]给出的地球参考椭圆计算所需的球大圆距离。在得到AIS数据集中的各个目标的距离和径向速度后，查找具有与所选目标相同的距离和径向速度的 AIS目标数据，即可实现雷达数据与AIS数据的匹配。

如果因为AIS系统覆盖不全、目标船只AIS系统关机或故障等原因，未能查找到所选目标所对应的AIS数据，则可以选取另一个大信噪比孤立目标回波，并重复上述步骤。如果出现雷达数据与两个或者多个 AIS数据匹配(此现象在实际观测中较为罕见)，则可直接放弃该雷达回波和对应的几组AIS数据，转而考察下一个大信噪比孤立目标回波，这并不影响算法的正常工作。以上的数据匹配过程只需要目标相对于雷达的距离和径向速度，而不需要使用目标方位角信息。

需要指出的是，上述数据匹配的过程是首先对雷达数据进行筛选，而后在AIS数据中搜索对应数据点，而不是先对AIS数据进行筛选而后搜索对应的雷达数据。这样做的目的在于提高效率。因为阵列校正需要大信噪比目标，而目标信噪比只有通过雷达数据才能体现，通过上述的第(1)步筛选过程(门限筛选)即可将大量小目标滤除，大大降低了后续搜索的工作量。

实现高频地波雷达数据与AIS数据的同步和匹配之后，则可以使用AIS信息进行天线阵校正。

3 使用AIS信息进行天线阵校正

本节将以高频地波雷达中普遍采用的直线阵作为基础进行讨论，但其结果可以推广至更一般的阵列，如方阵、L形阵等。

对于包含N个阵元的等间隔直线阵，当单个平面波信号照射该阵列时，阵列快照(snapshot)可以表示为[12]

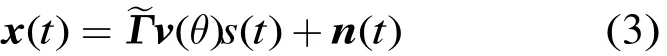
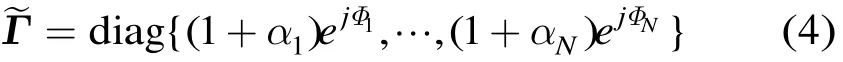
其中αn和φn分别为各个阵元增益和相位误差。

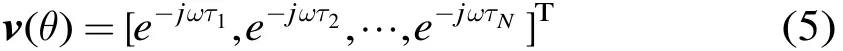
是平面波信号的阵列流型矢量，其中τn=(n-1)⋅si nθ⋅d/c,d是阵元间隔，θ是目标方位角(以阵列法向为参考点，逆时针为正)，ω为信号载波角频率，c为光速。

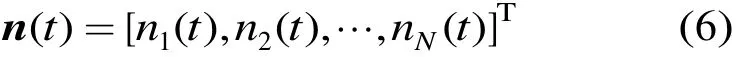
是阵列噪声分量。

不失一般性，将1号阵元作为参考阵元，则归一化后的阵列误差矩阵为

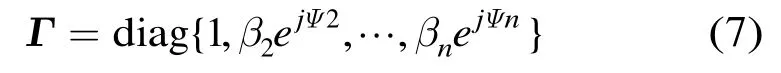
令所选取的目标回波信号的阵列快照为x(t)，以1号阵元为参考阵元，得到归一化之后的阵列流型矢量为

利用目标真实方位角θ，得到理想阵列流型矢量为

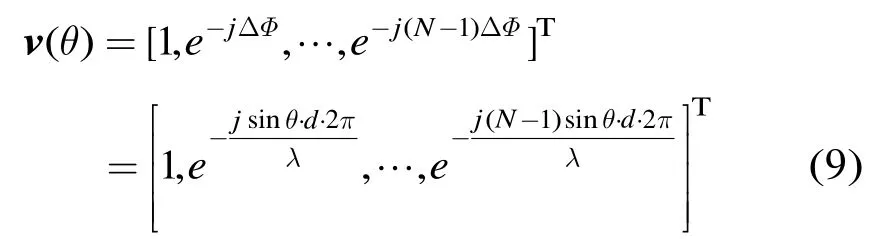
则阵列误差向量B为

其中“Ø”代表对应项相除。

阵列误差矩阵的估计值为

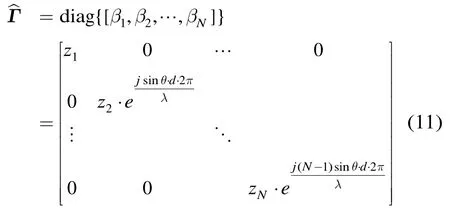
利用即可得到阵列校正矩阵Ccal

校正后的目标回波信号(阵列快照)为

经过式(8)到式(13)的校正过程，天线阵的相位和幅度误差将得到补偿，远场点目标所产生的平面波信号将在天线阵上呈现理想的线性相位曲线和均匀的幅度。

4 实测数据实验

本节使用高频地波雷达实测数据以及相应时段的AIS数据对新方法的性能进行测试。所采用的地波超视距雷达采用32元等间隔直线阵，阵元间距为15 m，阵列总长度465 m，沿海岸线布置。目标方位角θ以阵列法向为0°，顺时针为正。在雷达阵地附近，安装AIS接收机，在实验中，可接收到附近约100 km范围内装有AIS的船只发出的AIS信息。AIS信息以短信息方式发送，每一条信息均带有目标ID、时间戳(time stamp)、航行状态、航向、航速、经度、纬度等信息。表1给出了4条AIS信息作为示例。位于雷达阵地附近的AIS接收机，每小时平均可接收到20000条左右的AIS信息。高频地波雷达的距离门宽度超过2 km ，而AIS系统的定位精度可达 10-15 m[13]，远远高于高频地波雷达。在阵列校正过程中，对于数十千米之外的目标，其AIS数据的定位误差可以忽略，可以将AIS数据提供的目标位置作为其准确位置，并通过该数据解算出目标的真实方位角。

表1 AIS信息示例

在雷达观测范围内，存在大量舰船目标，图2中给出了高频地波雷达单个通道 (1号天线)的输出信号。雷达载频为4.040 MHz，相参积累时间(CIT)为217 s。在其距离-速度谱上100 km内可见大量具有较高信噪比的目标回波(图中已经将多普勒频率换算成径向速度)。使用第2节中介绍的方法选取了两个目标回波。两个目标回波的信噪比均在 30 dB以上，距离分别为82.3 km和73.9 km，径向速度分别为20.1 km/h和-22.6 km/h。其位置如图3所示。本实验中，1号目标将用于天线阵校正，2号目标将用于检验校正结果。作为对比，同时使用基于最大似然估计的盲校正算法[9]对该阵列进行校正，将其结果作为对照。

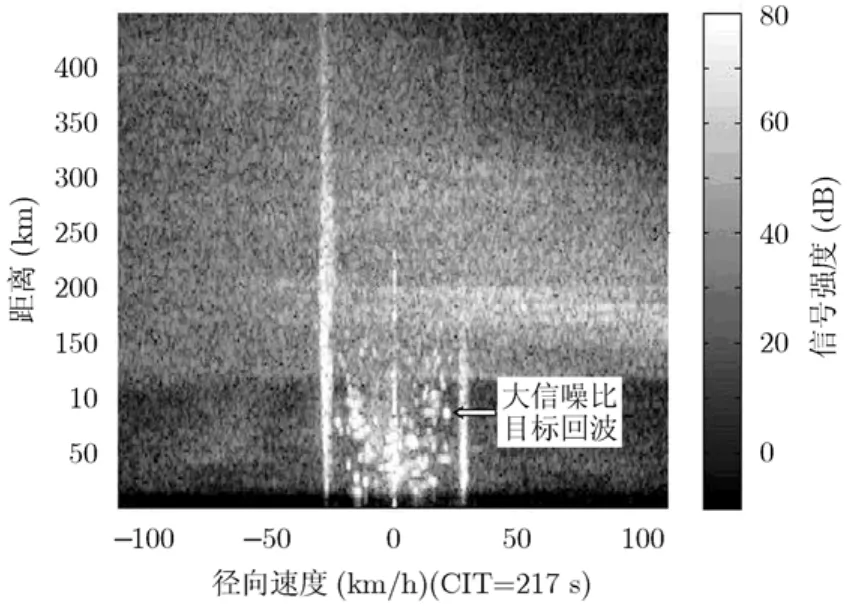
图2 单通道距离-速度谱

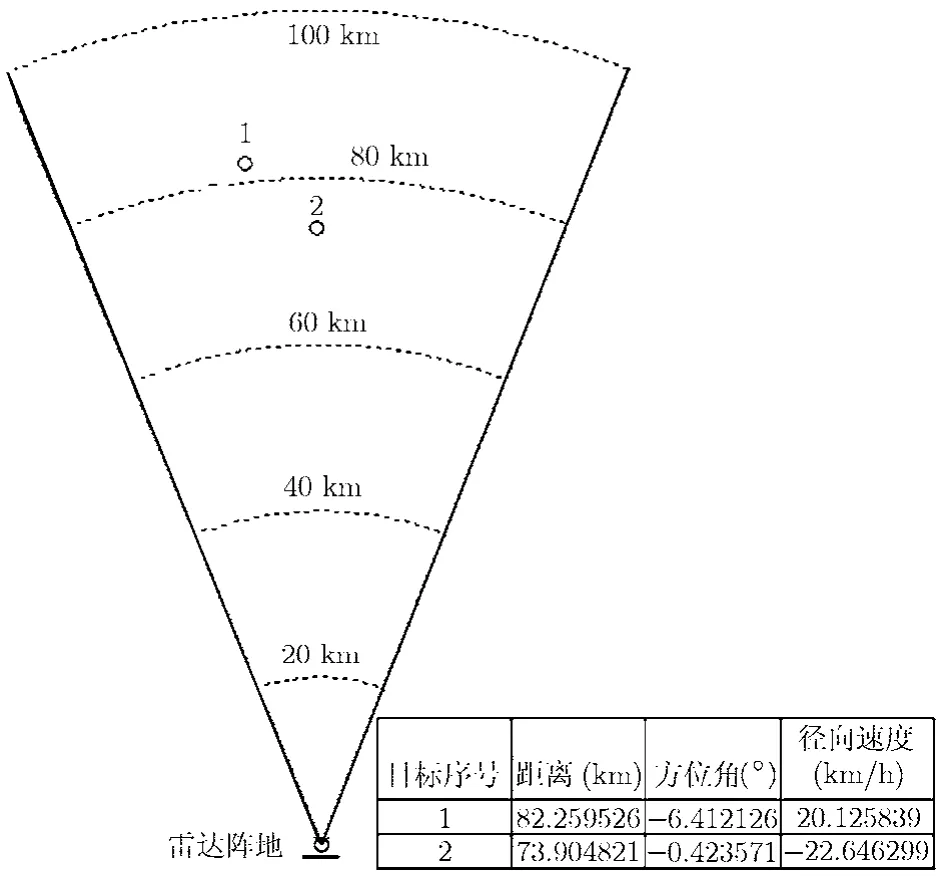
图3 所选取的目标位置示意图(利用AIS数据计算得到)

使用1号目标的回波和AIS数据求出阵列相位和增益误差，并用所得到的阵列校正矢量对天线阵进行校正，即按式(13)将校正前的阵列快照与校正矩阵相乘。图4和图5中分别给出了2号目标校正前后的相位曲线和幅度曲线。其中，图4中的理想相位曲线是利用目标的真实方位角计算得到的(真实方位角由AIS信息得到)，两幅图中均以1号阵元作为参考阵元。从校正结果中可以看到，新方法得到的目标相位曲线更加接近理想曲线，新方法得到的阵列增益更加均匀(即平面波信号在各个阵元上的信号强度更加一致)。校正前，天线阵的相位均方根误差为 21.5°，平均增益波动(增益的标准差)为8.7 dB；使用盲校正算法校正之后，相位均方根误差为10.9°，平均增益波动为2.4 dB；使用新方法校正之后，相位均方根误差为2.8°，平均增益波动为0.6 dB。可见，新方法的性能明显优于盲校正算法。

阵列校正的最终目的是提高目标方位角估计精度，使用MUSIC算法[14]求出阵列校正前后2号目标回波的空间谱，如图6所示。图中可以看到，两种阵列校正方法都可以提高方位角估计精度，而且在经过天线阵校正之后，目标回波的空间谱得到了锐化；新方法的校正精度更高，使用新方法校正后，目标回波空间谱的峰值位置更加接近目标真实方位角，因而可以得到更高的方位角估计精度。

新方法优于盲校正算法的根本原因在于，新方法通过使用AIS信息获得了目标的真实方位角，无须对目标方位进行估计，从而避免了由于目标方位角估计误差而导致的额外的阵列校正误差。而使用非合作目标的盲校正方法必须对目标的方位角进行估计，因而不可避免地受到了方位角估计误差的影响，从而影响了最终的阵列校正精度。此外，新方法无须进行反复迭代，因此其计算量小于盲校正算法。

5 结论

本文提出了使用AIS信息进行高频地波雷达天线阵校正的方法，利用高信噪比舰船目标回波与相应的AIS数据构造“合作目标”以实现高精度的天线阵校正。该方法可以得到高于盲校正算法的阵列校正精度，同时又无需部署专用信号源，且可以做到随时校正，是一种高性能低成本的天线阵校正方法。本文中使用高频地波雷达实测数据验证了新方法的优势。该方法不仅可以应用于传统岸基高频地波雷达，未来亦可应用于舰载高频地波雷达。

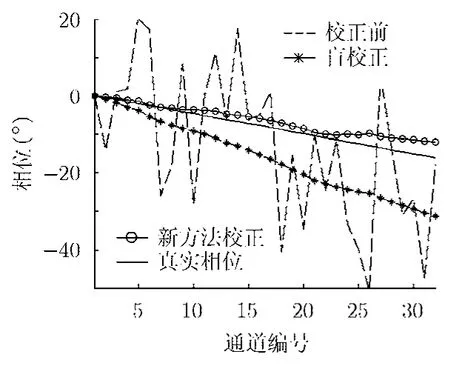
图4 天线阵校正前后的目标回波相位曲线(2号目标)

图5 天线阵校正前后的目标回波幅度曲线(2号目标)

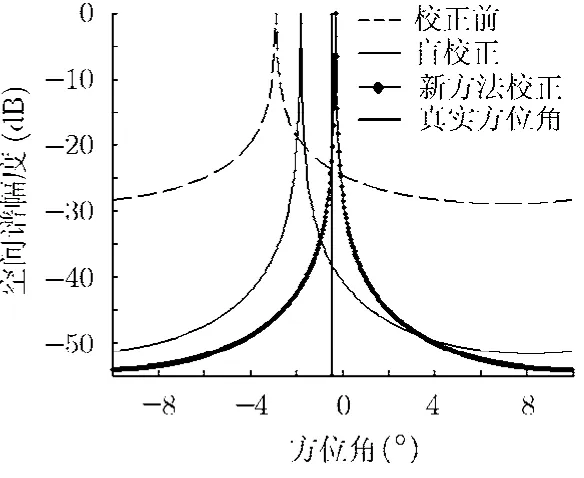
图6 阵列校正前后的目标回波空间谱(2号目标 MUSIC谱)

[1]He Ke,Zhang Xiao-min,Han Peng,et al..A calibration algorithm for nonplanar array with arbitrary geometry using known sources[C].Second International Conference on Computer Modeling and Simulation,Sanya,China,2010,Vol.1: 489-492.

[2]Wiegmann R.Antenna array calibration employing calibration beacons and steering vector estimation[C].Eleventh International Conference on Antennas and Propagation Conference Publication,Manchester,UK,2011,Vol.1: 41-44.

[3]Zhang Yu-feng,Ma Hong,and Tan Ping.A low complexity calibration method of gain and phase error for arrays with arbitrary geometry[C].2011 International Conference on Multimedia Technology (ICMT),Hangzhou,China,2011:3342-3345.

[4]Solomon,I S D,Gray D A,Abramovich Y I,et al..Over-thehorizon radar array calibration using echoes from ionised meteor trails[J].IEE Proceedings-Radar,Sonar and Navigation,1998,145(3): 173-180.

[5]Song Xiao-guo,Wei Yin-sheng,Cui Yan,et al..A novel array calibration method based on spatial correlation matrix for HFSWR[C].IEEE 10th International Conference on Signal Processing (ICSP),Beijing,China,2010: 344-347.

[6]Pouyan P,Marius P,and Gershman A B.Direction-of-arrival estimation and array calibration for partly-calibrated arrays[C].IEEE International Conference on Acoustics,Speech and Signal Processing (ICASSP),Prague,Czech,2011:2552-2555.

[7]Dai Ji-sheng,Zhao De-an,and Ye Zhong-fu.DOA estimation and self-calibration algorithm for nonuniform linear array[C].2010 International Symposium on Intelligent Signal Processing and Communication Systems,Chengdu,China,2010: 1-4.

[8]Efstathopoulos G and Manikas A.A blind array calibration algorithm using a moving source[C].The 5th IEEE Sensor Array and Multichannel Signal Processing Workshop,Darmstadt,Germany,2008: 455-458.

[9]Boon Chong Ng,Chong Meng Samson See.Sensor-array calibration using a maximum-likelihood approach[J].IEEE Transactions on Antennas and Propagation,1996,44(6):827-835.

[10]Vesecky J F,Laws K E,Paduan J D.Using HF surface wave radar and the ship Automatic Identification System (AIS)to monitor coastal vessels[C].2009 IEEE International Geoscience ＆ Remote Sensing Symposium,Cape Town,South Africa,2009: 761-764.

[11]Moritz H.Geodetic Reference System 1980[S].Bulletin Géodésique,Vol 54:3,1980.

[12]Solomon I S D,Gray D A,Abramovich Y I,et al..Receiver array calibration using disparate sources[J].IEEE Transactions on Antennas and Propagation,1999,47(3):496-505.

[13]Lin Chang-chuan,Qiu Hai-qin,Qian Yao-yu,et al..Chinese AIS network and impact on the maritime management[C].2010 International Conference on Internet Technology and Applications,Wuhan,China,2010: 1-4.

[14]Schmidt R O.Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Antennas and Propagation,1986,34(3): 276-280.