基于压缩感知的下视三维SAR成像新方法
李学仕 孙光才 徐 刚 邢孟道 梁 毅
(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
1 引言
传统的合成孔径雷达(Synthetic Aperture Radar,SAR)只能得到场景的 2维像,现实中,各种各样的应用需求都需要雷达具有下视3维SAR成像能力,如特殊地形的勘探、测绘、城市规划以及环境破坏的影响分析等[1,2]。传统的单基雷达无法工作于下视,这是由于飞行航迹左右两侧的点多普勒特性一致,跨航向方向没办法得到分辨。为了获取这一维的分辨,通常需在跨航向维摆放一个线性阵列或等效阵列。然而,跨航向维的分辨率与线阵长度密切相关,这就要求阵列天线长度不能太短。由于阵元间距必须小于1/2波长,才能保证天线方向图不会出现栅瓣,因此在孔径长度不能太短的情况下,阵元数就会非常多。然而在实际应用中,由于线性阵列天线设计的成本和实现的复杂度等问题,使得我们无法使用这样大型的阵列。
近年来,压缩感知(Compressed Sensing,CS)的概念被提出,它使得信息理解和获取等方面发生了革命性的变化,各国掀起了 CS理论在信号处理应用等领域的研究热潮[3,4]。由 CS理论可知,在满足有限等距性质(Restricted Isometry Condition,RIC)准则的情况下,通过构造有效的稀疏表征基利用求解最小l1-范数正则化问题,目标就可以从有限的观测样本中以极大的概率得到完美恢复,并且具有良好的抗噪性能[5-7]。基于这些特性,CS技术已经推广到与SAR相关的诸多领域,文献[8]针对在逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)系统中,方位采样缺损的情况下,通过构造方位稀疏的 ISAR成像模型,建立稀疏表征域及基空间表达式,通过优化方法来求稀疏解,该方法对实测数据的处理获得了良好的结果。文献[9]针对条带体制下的SAR成像,提出基于场景方位向小波稀疏表示的压缩感知成像方法,实测数据成像结果表明所提算法具有较好的有效性。文献[10]把CS技术运用到3维层析SAR中,通过实测数据处理验证了CS方法在3维层析SAR中应用的合理性。从这些研究成果中可以看出,CS在ISAR成像、SAR成像、3维SAR层析等方面具有独特的优势。本文正是基于 CS的思想,在采用跨航向维稀疏阵列配置下,研究下视3维SAR成像新方法。
本文内容安排如下:第1节为引言;第2节建立了下视3维SAR成像几何模型,进行了双通道等效单通道处理的公式推导,并讨论了多发多收线阵天线的工作形式以及下视3维SAR成像场景稀疏性分析;第3节介绍了基于CS理论的下视3维SAR成像方法;第4节给出了整个成像处理流程;第 5节对 CS理论强调要满足的两个条件进行了详细的分析;第6节通过仿真数据处理,验证了本文提出算法的有效性;第7节对全文进行了总结。
2 下视3维SAR成像几何模型
下视3维SAR成像几何模型如图1所示,载机平台高度为h,沿航向速度为v,设载机位于O点时的时刻为沿航向慢时间tm的起点,线阵天线阵元沿跨航向稀疏分布,由上一节分析知,在实际应用中由于线阵天线设计的成本及复杂度等问题,要求阵元在跨航向维采用稀疏布阵的方式。
2.1 双通道等效单通道处理
这里下视3维SAR成像采用多发多收模式,根据等效相位中心原理,当收发分置的两个天线之间基线长度相对于作用距离很短时,可以等效为两者连线的中心作自发自收的单通道工作模式,但需要补偿一个常数相位[11],这样处理可以避免由于发射天线、接收天线之间存在一定的水平基线而导致回波信号斜距历程表现为双根号形式。
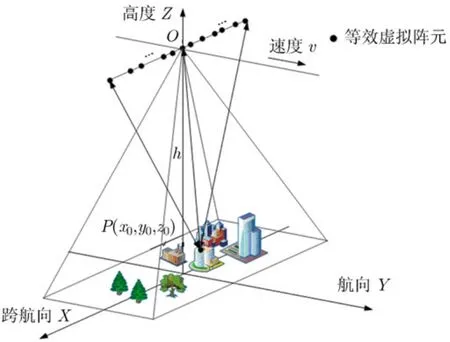
图1 下视3维SAR成像几何模型
如图1所示,经过tm时间后,任意一发射天线的位置坐标可以表示为(xT,vtm,h),任意一接收天线的位置坐标可以表示为(xR,vtm,h),则场景中点目标P的收发斜距分别为
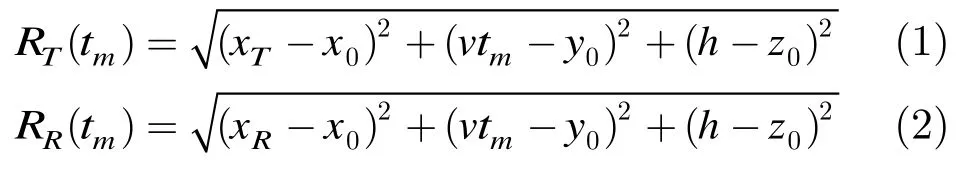
收发天线的等效相位中心到P点的距离为
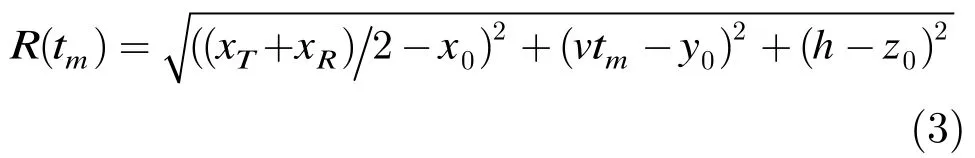
则等效之前与等效之后收发双程的距离差为
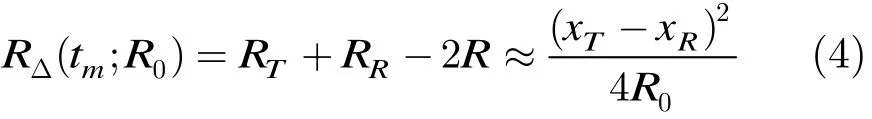
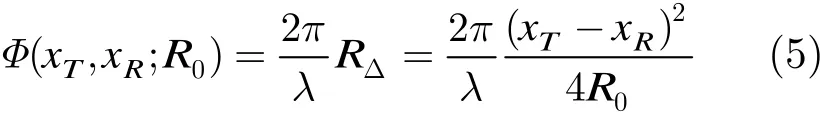
从式(5)可以看出,补偿的相位依赖于场景中不同的点目标位置,但通常取载机正下方的点对应的垂直距离来代替R0,由此引入的误差通常是可以忽略的,如线阵天线长度为8 m,发射信号波长为0.03 m,载机平台高度为10 km,跨航向波束宽度为20o,则由此导致的相位误差小于π/100,这个误差在成像处理中是可以忽略的,因而可以对成像场景进行统一的相位补偿。
2.2 多发多收线阵天线的信号形式
采用等效相位中心原理,虽然可以简化系统回波的收发模型,但是并不能增加天线有效阵元的数量。为了基于有限的阵元,获得更多的等效阵元数,这里采用多发多收模式,在少量阵元数情况下可以获得更多的有效阵元。多发多收线阵天线有两种工作方式,如图2所示,所有阵元都同时具有发射和接收功能。第1种如图2(a)所示,发射天线不同时刻顺序发射信号,全部接收天线同时接收回波信号,当所有发射天线依次执行完一次发射时称为一个周期。第2种如图2(b)所示,双发射天线同时发射正交或近似正交的两路信号,比如正负调频信号,在接收端通过校正处理分离正交的两路信号,从而区分出不同发射阵元发射的信号,同样,当所有发射天线都执行完一次发射时为一个周期。为了获得较多的等效相位中心,这两种工作方式,都需要把一个周期内的等效相位中心校正到某个参考时刻处。从信号处理的角度可以知道,不同发射时刻的信号等效认为是存在一个时间的延时,将两维的相位中心投影到某参考时刻可以认为是在航向维做时间的平移,可以通过在航向维对应的频域乘线性相位操作来完成。经过处理后,就得到一个排列相对紧密的线阵,如图2中的参考位置。此时可以认为相对紧密的阵列在对地面目标进行观测。
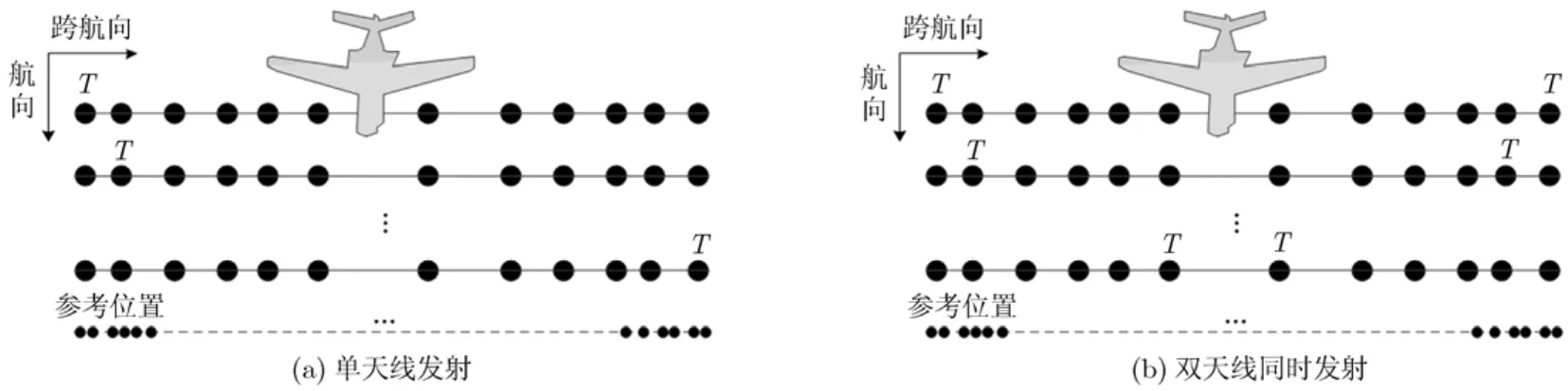
图2 多发多收线阵天线信号形式示意图
2.3 下视3维SAR成像稀疏性分析
下视3维SAR成像场景沿航向的一个切面如图3所示,在跨航向维,除极少数连续的成片目标外,大多数目标与跨航向维分辨率相比,都可视为点目标,而且,成片的目标如绿色植被等通常认为是连续的背景,可以将其视为噪声处理。下视3维SAR成像实际是对场景目标的轮廓进行成像,这样对每个高度单元而言,如图中的虚线所示,场景都满足稀疏性,上述因素决定下视3维SAR场景是可以被稀疏重建的。
3 下视3维SAR成像算法
经过等效相位中心处理,就可以认为收发双通道做单通道自发自收。下面将主要分析稀疏等效相位中心阵列配置下的下视3维成像算法。
3.1多通道航向维处理
经过第2节的处理后,可以认为是在参考位置处一个排列相对紧密的线阵在做自发自收操作,这样tm时刻第n个等效相位中心的位置坐标可以表示为(xn,vtm,h),其中xn为第n个等效相位中心在跨航向的位置,则等效相位中心到P点的距离可以表示为
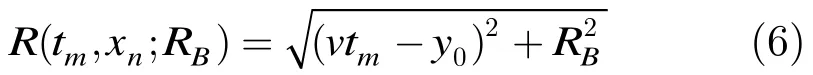
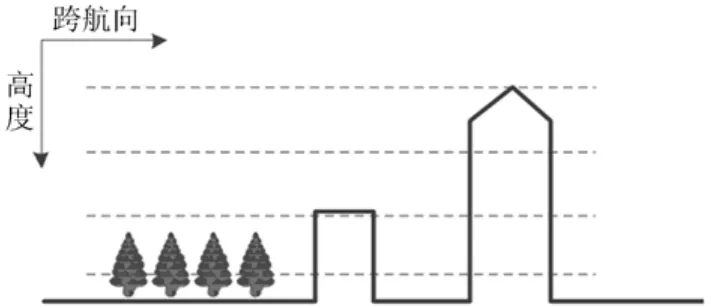
图3 高度-跨航向2维场景平面
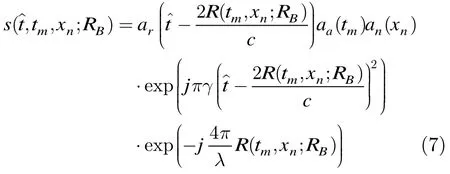
对每一个阵元而言,其录取的信号可以认为是正侧视情况下的回波数据。针对每个阵元的多次回波信号,可以采用传统的成像处理算法对其进行成像处理。由于传统成像算法比较成熟,加之本文的重点是跨航向维的稀疏处理,这里对每个阵元的航向维成像不做更多的叙述。这里假设每个阵元的信号都经过RD算法处理。经过成像处理后,各阵元信号可以表示为
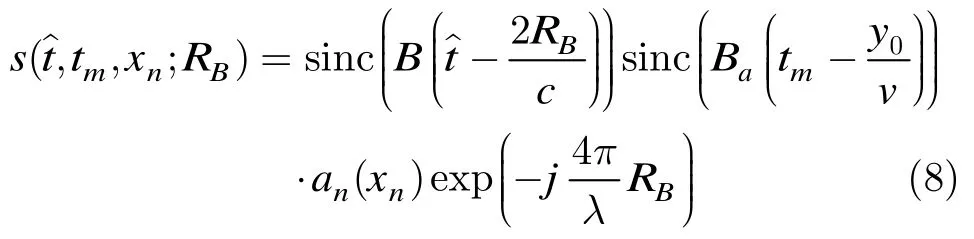
其中B为发射信号带宽,Ba为航向维带宽。经过航向维处理之后,下面将分析高度和跨航向维处理。
3.2 高度和跨航向2维处理
将式(8)变换到高度维频域得

其中Ar表示发射信号窗函数ar(·)的频域形式,fr为高度维频率,fc为发射信号载频,将式(9)变换到跨航向维频域可以得到两维傅里叶表达式。由于跨航向维采用稀疏布阵的方式,所以对式(9)进行跨航向维的傅里叶变换要利用傅里叶变换的定义,设傅里叶变换矩阵为ψ,其表达式形式为
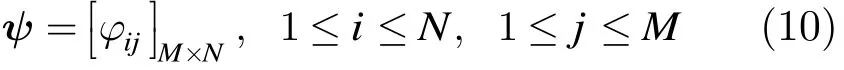
将式(9)变换到2维频域后,进行高度和跨航向维的徙动校正、二次脉冲压缩后,变换到2维时域进行跨航向维dechirp处理,然后进行跨航向维傅里叶变换即完成了成像处理过程,其中徙动校正函数和二次脉冲压缩函数分别为
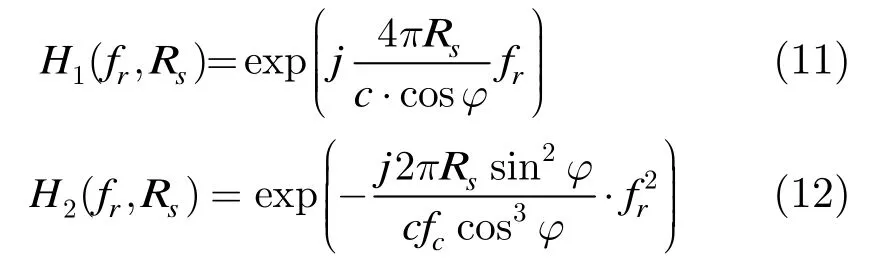
其中φ为点目标到阵元的斜视角,Rs为选定的参考距离。下面把式(9)之后的操作写成矩阵表示形式为
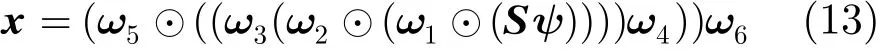
其中x表示成像结果,ψ表示跨航向维傅里叶变换矩阵,ω1~ω6分别表示徙动校正,二次脉冲压缩,高度维逆傅里叶变换,跨航向维逆傅里叶变换,跨航向维dechirp处理,跨航向维傅里叶变换操作对应的矩阵形式。实际处理时,是把x与S表示为长列向量的形式,这样上述的操作都可以写成矩阵左乘S的形式,如式(14):
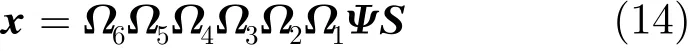
其中Ψ表示ψ对应的操作,Ψ的矩阵形式是以ψ为对角元素的一个大矩阵,Ω1~Ω6表示ω1~ω6对应的操作,同样都是以矩阵ω的元素构成的大矩阵,并用A表示上述所有的操作,则式(14)可以写成下面的表达式:

这里,S可以看作是观测信号,x看作为要恢复的原始场景,这样把式(15)写成下面的形式:

其中Φ表示A的反操作,由CS理论知,x可以通过l0-范数最小化进行重建。
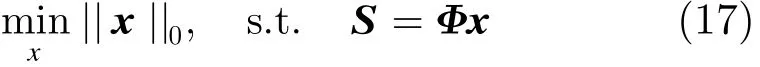
这是一个NP难题,一般地,采用l1-范数来逼近l0-范数,从而获得稀疏解[12,13]。此时问题变为
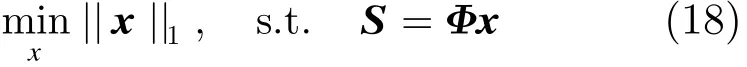
在高度不确定的系统中,要获得有效解,CS理论强调要满足两个条件[6,7]:第一,场景要满足稀疏性,由第2节分析知,这一点是满足的。第二,观测矩阵要满足RIC准则。观测矩阵的RIC特性与等效相位中心的摆放有关,因此我们可以通过设置收发天线的位置来得到较好的结果,这将在第4节中单独进行讨论。于是式(18)的求解可以转化为优化问题求解,构造代价函数为
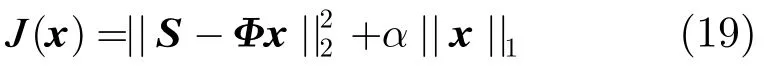
式(19)中,第1项为观测误差,第2项为点目标特性增强,系数α主要平衡两者之间的关系,其值的大小可以通过统计参数估计得到,具体计算方法可以参见文献[6]。式(19)的求解需要数值迭代算法,由文献[14]知,基于常规Hess矩阵的牛顿或者拟牛顿算法,其求解结果一般较差,因而本文采用基于更新Hess矩阵的拟牛顿算法对上式进行求解[14]。
为避免l1-范数在零处不可导问题,对式(19)进行近似得
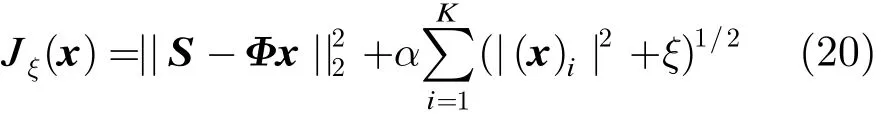
其中ξ为一个很小的正数。对式(20)进行求梯度得
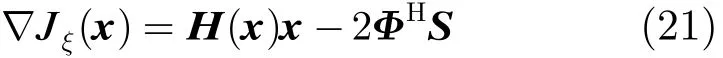
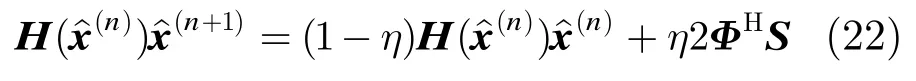
其中η为迭代步长因子,式(22)迭代终止的条件为δ为一个很小的正数。
4 下视3维SAR成像算法流程
经过第3节的处理,就可以对下视3维目标进行SAR成像了。本文给出方法的处理流程如图4所示。对于多通道收发系统而言,首先是等效相位中心处理,经过处理后多通道收发系统可以近似为是各阵元独立收发。然后对每个阵元进行航向维处理,航向维的处理可以看作是传统的正侧视情况,因而可以采用RD算法进行实现,需要注意的是在航向维的频域要进行相位补偿,将一个周期内的等效相位中心校正到同一条直线上,从而得到一个排列紧密的线阵。对每个阵元成像处理后,接下来就是跨航向的处理,进行高度和跨航向维成像,这两维的处理相当于是考虑弯曲校正的dechirp处理,由于跨航向维采用稀疏布阵方式,因而在这两维结合稀疏信号处理方法进行成像,最终通过正则化问题求解得到下视3维SAR图像。
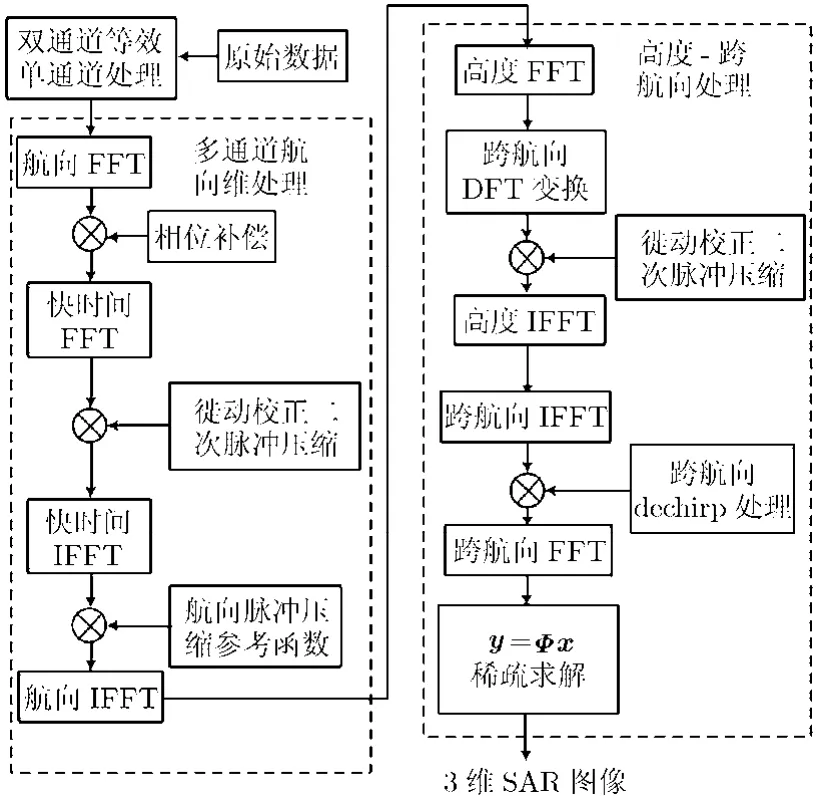
图4 下视3维SAR成像处理流程
5 阵列配置与RIC准则
根据稀疏信号处理理论可以知道,下视3维场景能否被正确重建,取决于两个因素[6,7]:第一,场景的稀疏度,第二,观测矩阵Φ是否满足RIC准则。
在前面分析知,下视3维SAR场景是满足稀疏特性的。下面主要分析观测矩阵Φ的RIC特性。RIC准则最早由Candes和Tao提出,当观测矩阵Φ满足RIC条件时,则观测矩阵的列可以近似看作为一个正交的系统。为详细分析阵元分布对观测矩阵RIC条件的影响,先从简单的情况分析,就是不考虑弯曲校正的情况,这时Φ就是一个逆傅里叶变换(IDFT)矩阵,维数为N×M。当考虑徙动校正的情况时,要把观测数据和原始场景数据分别写成列向量的形式,这时Φ就为一个大矩阵,其维数为O(N×L)×O(M×L),其中L为高度向采样点数,两者对于阵元分布对观测矩阵的 RIC影响是相似的,而且当观测矩阵维数较小时,更便于观察仔细。
阵元分布如图5所示,进行等效后虚拟阵元位置如图6所示,不考虑弯曲情况下,此时得到观测矩阵Φ的列自相关矩阵如图7所示,观测矩阵的每一列表示点目标的回波,观测矩阵的列自相关矩阵表示两点之间的相关性,从理论上讲两点相邻越近则相关性越大,如两个点在一个分辨单元之内,两点相邻越远则相关性越小,如两个点在一个分辨单元之外。从仿真中也可以看出矩阵Φ的列自相关矩阵很接近一单位阵,这说明观测矩阵Φ满足RIC特性[15]。
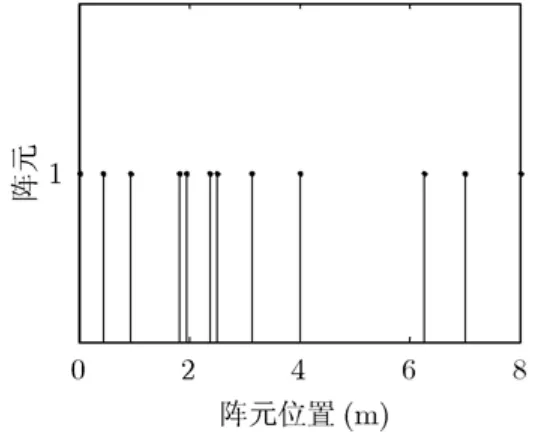
图5 等效前阵元摆放位置
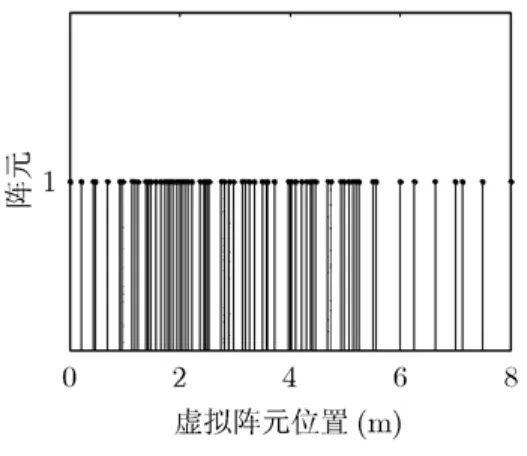
图6 等效后虚拟阵元位置

图7 观测矩阵Φ的列自相关矩阵
由于不考虑徙动校正的情况,沿跨航向维会带来几何形变,同一高度单元的点聚焦之后分布在不同的高度单元。因而要进行徙动校正,这样同一高度单元的点成像后仍在同一条直线上。这时对观测矩阵进行RIC测试结果如图8所示,从局部放大图可以看出,矩阵Φ的列近似满足正交性,说明矩阵Φ仍满足RIC特性。图8之所以没有像图7一样,这是把左乘、右乘、点乘矩阵都写成左乘矩阵形式所决定的。
6 仿真数据处理结果与分析
为验证本文算法的有效性,下面进行点目标仿真验证,具体仿真参数如表1所示。
本仿真中采用的阵元分布如图5所示,场景中点目标分布位置如图9所示。共9个点,分布在3个高度上,地平面上分布4个点,关于中心对称成十字摆放,跨航向维两点相距200 m,沿航向两点相距400 m。高度为30 m的地方分布一个点,在航向和跨航向2维平面的中心位置处。高度为60 m同样分布4个点,其在航向和跨航向2维平面的位置与地平面上的点分布相同。
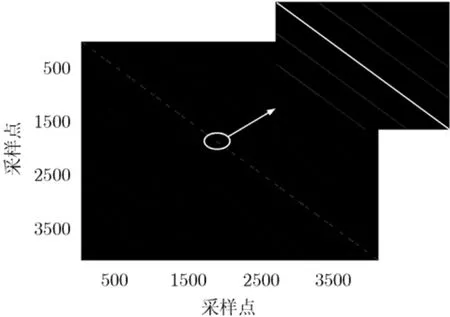
图8 观测矩阵Φ的列自相关矩阵

表1 仿真参数设置
采用本文的处理方法,即图4的处理流程,成像结果如图10所示,成像后点目标位置与原始场景中点目标位置基本相同,从成像效果可以看出本文算法是有效的。为进一步验证本文所提算法,对沿航向位置为零处进行切片处理,并对直接采用dechirp算法进行成像,与本文采用CS方法在相同条件下进行比较,其中图11为直接采用dechirp算法成像结果,图12为采用本文算法成像结果。图13(a)为图11中A1点的等高线图,图13(b)为图12中A2点的等高线图,从图13(a)可以看出直接采用dechirp算法成像时,跨航向维旁瓣非常严重,图中旁瓣的形状是由于在时宽-带宽积较小的情况下,对跨航向维旁瓣进行徙动校正时发生错误,导致旁瓣与主瓣落在不同的高度单元内[16],而采用本文提出的算法,如图13(b)所示,旁瓣得到有效的抑制,等高线图很规则,主瓣旁瓣能够明显分开,说明成像效果良好,以上进一步验证了本文提出算法的有效性。
7 结束语
本文研究了基于CS思想的下视3维SAR成像算法,解决了垂直航向维实孔径天线成像对阵元间距的限制问题。文中首先给出了双通道等效单通道处理需补偿的相位项,同时介绍了多发多收模式下线阵天线的工作形式,在此基础上本文对下视3维SAR成像处理算法进行了研究,并给出了整个成像处理过程的流程图。文中还对 CS处理需满足的两个条件进行了详细的分析,验证了CS方法在下视3维SAR成像处理中应用的合理性。最后,通过仿真数据处理验证了本文所提算法的有效性及正确性。
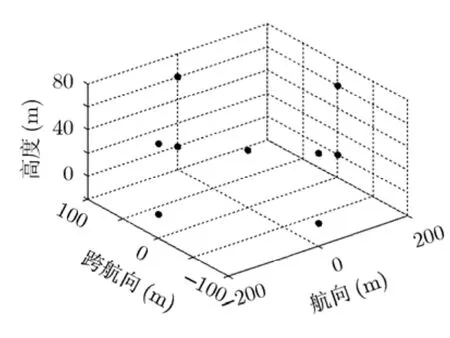
图9 点目标分布位置
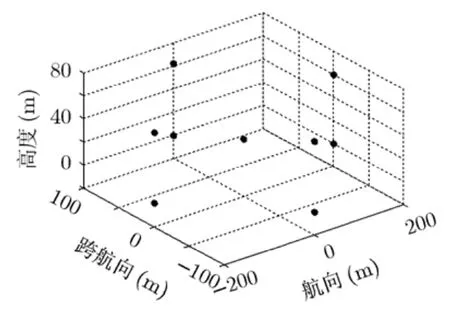
图10 点目标成像结果
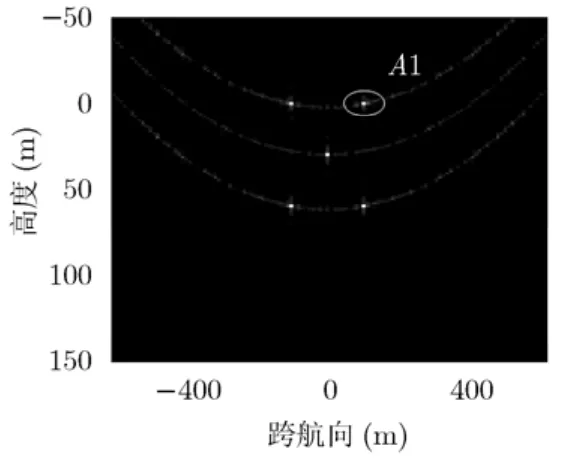
图11 直接采用dechirp算法成像结果
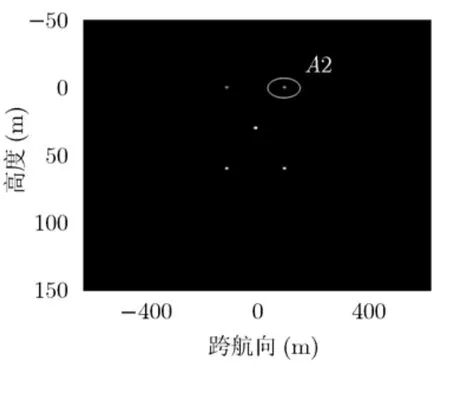
图12 本文成像算法

图13 点目标等高线图
[1]Klare J.A new airborne radar for 3D imagingsimulation study of ARTINO[C].European Conference on Synthetic Aperture Radar,Germany,May 16-18,2006:1-4.
[2]Fery O and Meier E.3-D Time-domain SAR imaging of a forest using airborne multibaseline data at L- and P-bands[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(10):3660-3664.
[3]Potter L C,Ertin E,Parker J T,et al..Sparsity and compressed sensing in radar imaging[J].Proceedings of the IEEE,2010,98(6):1006-1020.
[4]Zhang Y X,Sun J P,Tian J H,et al..Compressed sensing SAR imaging with real data[C].International Congress on Image and Signal Processing,Yantai,China,Oct.16-18,2010:2026-2029.
[5]Ji S H,Xue Y,and Carin L.Bayesian compressive sensing[J].IEEE Transactions on Signal Processing,2008,56(6):2346-2356.
[6]Candes E J and Tao T.Near-optimal signal recovery from random projections:universal encoding strategies?[J].IEEE Transactions on Information Theory,2006,52(12):5406-5425.
[7]Candes E J and Tao T.Decoding by linear programming[J].IEEE Transactions on Information Theory,2005,51(12):4203-4215.
[8]Li Jun,Xing Meng-dao,and Wu Shun-jun.Application of compressed sensing in sparse aperture imaging of radar[C].Asian Pacific Conference on Synthetic Aperture Radar Proceedings,Xi,an,China,Oct.26-30,2009:651-655.
[9]王伟伟,廖桂生,吴孙勇.基于小波稀疏表示的压缩感知SAR成像算法研究[J].电子与信息学报,2011,33(6):1440-1446.Wang Wei-wei,Liao Gui-sheng,and Wu Sun-yong.A compressive sensing imaging approach based on wavelet sparse representation[J].JournalofElectronics&Information Technology,2011,33(6):1440-1446.
[10]Zhu X X and Bamler R.Tomographic SAR inversion byL1-norm regularization-the compressive sensing approach[J].IEEE Transactions on Geoscience and Remote Sensing,2010,48(10):3839-3846.
[11]梁毅.调频连续波SAR信号处理[D].[博士论文],西安电子科技大学,2009.Liang Yi.Signal processing of FMCW synthetic aperture radar data[D].[Ph.D.dissertation],Xidian University,2009.
[12]Chen S,Donoho D L,and Saunders M.Atomic decomposition by basis pursuit[J].SIAM Journal on Scientific Computing,1998,20(1):33-61.
[13]Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[14]Cetin M and Kard W C.Feature-enhanced synthetic aperture radar image formation based on nonquadratic regularization[J].IEEE Transactions on Image Processing,2001,10(4):623-631.
[15]Alonso M T,López-Dekker P,and Mallorquí J J.A novel strategy for radar imaging based on compressive sensing[J].IEEE Transactions on Geoscience and Remote Sensing,2010,48(12):4285-4295.
[16]Moreira A,Mittermayer J,and Scheiber R.Extend chirp scaling algorithm for air- and spaceborne SAR data processing in stripmap and ScanSAR imaging modes[J].IEEE Transactions on Geoscience and Remote Sensing,1996,34(5):1123-1136.

