基于二阶锥优化方法的MIMO阵列发射方向图设计

高 伟 黄建国 徐振华 张群飞

(西北工业大学航海学院 西安 710072)

1 引言

近年来在 MIMO通信技术快速发展与成熟促使下，MIMO雷达和声呐等新技术逐渐成为研究热点[1,2]。MIMO雷达与声呐阵列系统与常规相控阵列系统的根本不同在于前者充分利用了发射波形分集和空间分集技术，能够形成大的虚拟阵列孔径，增加了空间独立信道及更高的自由度，因此能够克服目标回波的闪烁，从而提高信号检测器的性能；而后者是利用发射信号的相关性最大化相干处理增益。按阵列传感器排列方式的不同MIMO雷达与声呐阵列又可分为分布式 MIMO阵列和集中式MIMO阵列。分布式MIMO阵列通过空间远距离位置放置发射和接收阵列的阵元可以获得目标的角度扩展。集中式MIMO阵列的特点是发射和接收阵元间距较小，相对于传统相控阵雷达，集中式MIMO雷达具有更高的分辨率、对低速运动目标检测的灵敏度和更好的参数识别能力[1]。

随着MIMO雷达和声呐研究工作的展开，由于MIMO阵列可同时获得相干处理增益和空间分集增益结构特征，通过灵活设计发射信号可以综合出适用于不同情况下的实际发射方向图，因此MIMO阵列的波形设计成为一个重要的研究主题。在发射信号优化方面，MIMO 雷达发射波形设计方法众多[3,4]，主要可分为3类：(1)基于协方差矩阵设计；(2)基于模糊度函数设计；(3)基于先验信息设计。已有研究为对发射信号相关矩阵进行Cholesky分解，对分解因子用梯度搜索算法求得最优的发射波形相关矩阵[5]；在不同代价函数下优化发射信号互相关矩阵，使综合出的发射方向图逼近给定的理想发射方向图[6]；文献[7]以优化目标参数估计为目的，在推导出MIMO雷达目标参数估计的克拉美罗界(CRB)之后，通过最小化CRB矩阵的迹、行列式和最大特征值来优化发射信号的互相关矩阵；采用线性规划方法由一组基波束综合出发射方向图[8]。

这些已有的方法计算复杂度大，有些方法性能对初始参数选取比较敏感。本文基于任意发射方向图是一组基波束(对应一组基信号矢量)按一定比例组成的思想[8]，先在最小旁瓣约束条件下利用二阶锥优化(second-order cone programs)得出基波束的发射波形，然后利用线性规划求解出构成方向图的基波束(基信号矢量)的比例系数，所得 的发射方向图较其它方法具有更低的旁瓣和更加平滑的主瓣指向，且计算速度快。

2 发射方向图模型

考虑集中式MIMO阵列系统，在远场窄带假设条件下，发射阵列为均匀线列阵(ULA)且阵元数为M，其在空间中的归一化功率密度为

式(1)中θ和φ分别表示方位角和俯仰角，a(θ)=为M×1发射阵列导向矢量,其中f为发射信号频率，c为波速，d为发射阵元间隔；R为发射信号矩阵S的相关矩阵。

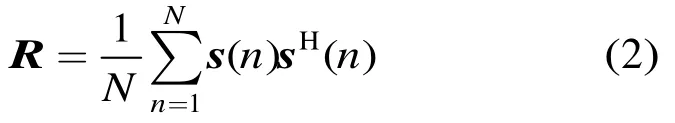
其中N为发射信号采样长度，…,sM(n)]T为第n个M×1发射信号向量。由式(1)可知，归一化功率密度P(θ,φ)即为我们所期望设计的发射波束。当阵列构型确定时，这一设计问题便转化为信号互相关矩阵R的设计问题。对于常规相控阵，发射信号完全相干，秩为1，其中θ0为目标方向，其发射方向图为pphased(θ)=对于MIMO阵列，发射信号正交时，R可等效为单位阵I，其发射方向图为pMIMO(θ0)。根据任意发射方向图可以由一组基波束合成的思想，由式(1)和式(2)可看出，发射方向图是由一个脉冲内的一组发射信号波束图aH(θ)s(n)⋅sH(n)a(θ)线性叠加组成，如式(3)所示。

式(3)中αn为基波束的权值系数。对式(3)中的基信号向量s(n)按权重αn进行合并，得到由主基信号向量的s(l)构成的发射方向图为

式(4)中αl为主基波束的权值系数。其中由主基信号向量的s(l)构成的基波束图Bl(θ,φ)为

将式(5)代入式(4)可得由主基波束图构成的发射方向图为

最后定义任意两个方向的互相关方向图如下：

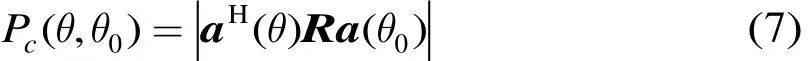
式(7)表示了两个不同方向上回波的相互干扰程度。

3 基波束的构造

综合出的发射方向图在更加逼近给定的理想波束图情况下，还需空域旁瓣和空域互相关系数越小越好，因此所要构造的基波束也必须具有低的空域旁瓣和空域互相关系数。切比雪夫窗函数法只适用于均匀线列阵，对平面阵等其它结构的基阵不适用，且性能调整不灵活。近年来出现了一些将优化理论运用于旁瓣控制的方法，例如采用二阶锥约束的方法实现任意期望主瓣响应或主瓣幅度响应的波束图设计，并且可以在波束主瓣宽度、旁瓣级、零陷干扰以及稳健性之间进行最佳折中[9]。本文采用主瓣宽度约束条件下的最低旁瓣波束形成方法，低旁瓣波束形成可以解释为在给定主瓣宽度的条件下，使旁瓣级最低；主瓣宽度越宽，能够获得的旁瓣越低。因此基于二阶锥优化方法可直接构造出主基波束图，其优点是在保证主基波束宽度满足条件的情况下具有更低的旁瓣级和空域互相关系数。

主瓣宽度约束条件下低旁瓣波束形成方法，可以表达为约束优化求解问题：在保证给定宽度波束对观察方向的响应为1的条件下，让旁瓣区域最大旁瓣值最小，它可以表示为

式中θ0为观察方向，Δθ为主瓣波束宽度的一半，w为所求的阵列加权向量。引入一新的非负实辅助变量γ和一组新的非负辅助变量θi∈θSL,i=1,…,I，其中θSL为旁瓣区域,θi为旁瓣区域离散方向的角度值，则式(8)可变为

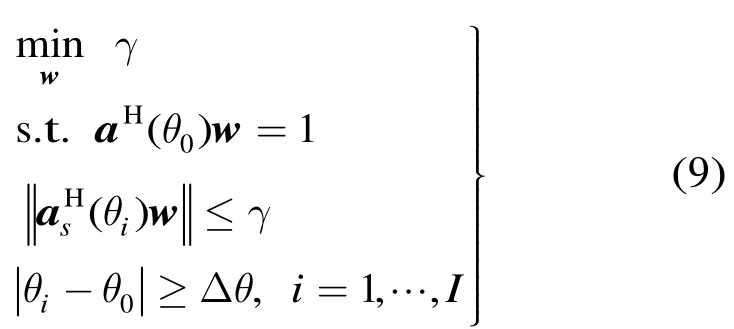
式(9)描述的是凸优化问题，可以转化为二阶锥优化的形式，二阶锥优化是凸优化可解标准问题的一种，然后利用已有的内点方法(interior-point methods)可以求出其数值解。式(9)使用Sturm开发的二阶锥规划Matlab工具箱SeDuMi可以很容易的求解数值解。该低旁瓣波束形成方法相比于采用低旁瓣的切比雪夫窗函数加权波束图和其它基于自适应波束形成的旁瓣控制方法的波束图，在同等主瓣宽度的情况下可以获得更低的旁瓣级。

4 发射方向图合成

在任意发射方向图可以由一组基波束合成的基础上，采用如下代价函数逼近理想方向图，

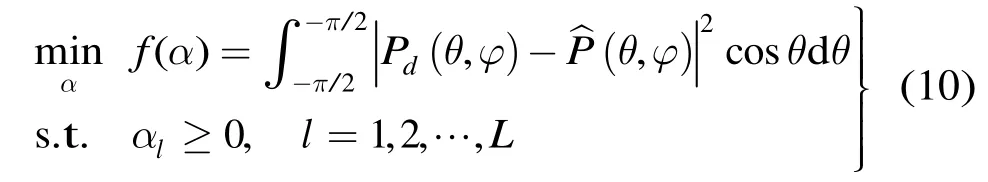
式(10)中Pd(θ,φ)为任意给定的理想方向图，θ为方位角，αl定义与式(4)相同。将上述代价函数离散化，再令俯仰角φ=0，后将式(6)代入式(10)可得

式(12)即为基于式(10)代价函数的发射方向图数学模型，它属于线性规划问题，其目标函数和L+M个约束函数都是线性的，并且它也是一类重要的凸优化问题。线性规划问题的解并没有一个简单的解析表达式，但是目前仍然有许多有效的方法来求解，包括 Dantzig方法和内点法等。由于线性规划问题的求解工具已经被广泛地嵌入到各种流行的软件工具中，因此在此不再赘述。

5 仿真结果

为了通过计算机仿真验证所提算法性能，采用如下仿真参数和条件：发射阵列为均匀线列阵(ULA)，阵元数为M1=1 0，阵元间隔为发射信号波长一半，离散方位角个数为360个。

取观察方向θ0=0o，半主瓣波束宽度Δθ=13.5o，比较均匀加权(常规)波束形成方向图，-20 dB切比雪夫窗函数加权波束形成方向图与基于二阶锥优化方法的主瓣宽度约束条件下低旁瓣波束形成方向图，如图1所示。由图可以看出基于二阶锥优化方法，半主瓣波束宽度 Δθ=1 3.5o约束条件下低旁瓣波束形成方向图与-20 dB切比雪夫窗函数加权波束形成方向图主瓣宽度近似相同但旁瓣级要低 4 dB，具有更低旁瓣级的性能。

选取理想方向图Pd(θm)为 (- 3 0o,30o)的矩形波束，虽然矩形波束宽度占整个观察方位角的 1/3，但初始时由于离散方位角个数为360个，所以初始基波束个数也取为 360个。根据式(12)对基波束分别进行计算，由基波束的权值系数α={αl},l=1,2,…,360的权重大小合并出 5个不同方向的主基波束图，其余基波束权值系数取0,5个主基波束图的指向和归一化的权值系数[8]分别为{-25.5°,-1 2.5°,0°,12.5°,25.5°}和{0.1989,0.2003,0.1994,0.2011,0.2003}。根据式(12)计算出基波束的权值系数后，再由式(6)得实际合成的发射方向图。为了比较各种方法设计发射方向图的性能，除了本文所提设计方法外，图2中给出了文献[10]中的设计方法由二阶锥规划MATLAB工具箱SeDuMi求得的发射方向图，以及由文献[8]中所提设计方法的发射方向图。由图2可看出本文所提方法(实线)比其它方法在主瓣区更加平滑接近理想矩形发射方向图，在旁瓣区具有更低且平坦的旁瓣级；其中以0°方向与其它方位角的互相关方向图为例，如图3所示。由图3可以看出本文所提设计方法的发射方向图的互相关旁瓣在3种方法中是最低的，与图2中合成方向图主瓣外旁瓣级最低相对应。

当发射阵元数M2=16且Pd(θm)取为 (-60o,-3 0o)∪ (30o,60o)两个方向的矩形波束时，同理可根据式(12)对基波束权系数进行合并后得出 6个不同方向的主基波束图，其余基波束权系数取为0,6个主基波束图的指向和归一化的权值系数分别为{- 5 5,-4 5,-3 5,35,45,55}和{0.1583,0.1643,0.1735,0.1758,0.1669,0.1612}。图4分别给出了3种方法对两个理想矩形方向图合成的实际发射方向图，由图4可看出本文方法在旁瓣区具有更低且平坦的旁瓣级；由图5所示的-45°方向和其它方位角的互相关旁瓣比较低，可得出本文方法在对两个理想矩形发射方向图进行合成时也具有较低的空域互相关旁瓣。其原因是本文所提的基波束构造方法是基于二阶锥优化的主瓣宽度约束条件下的最低旁瓣波束形成方法，该方法具有性能调整灵活且适用于各种不同结构的阵列。

以合成理想方向图Pd(θm)为 (- 3 0o,30o)的矩形波束为例，随着阵元数的增加，分别测试3个算法的运算时间。程序运行的硬件平台为双核2.93 GHz主频、2 G内存PC机，采用Matlab R2010a版使用相应的凸优化工具箱，为保证计时准确只对运算时间较长的凸优化代码部分进行计时得表1。由表1可看出本文方法比文献[10]的迭代方法要快的多，但本文方法与文献[8]方法计算时间相当。原因是两者同属于线性规划(linear programming)问题，并且本文方法采用基于二阶锥优化方法构造较低旁瓣的基波束计算时间有所增加，但是合成的实际发射方向图主瓣和旁瓣性能更优。

图1 基波束方向图比较

图2 合成的实际发射方向图

图3 0°方向与其它方位角的互相关方向图

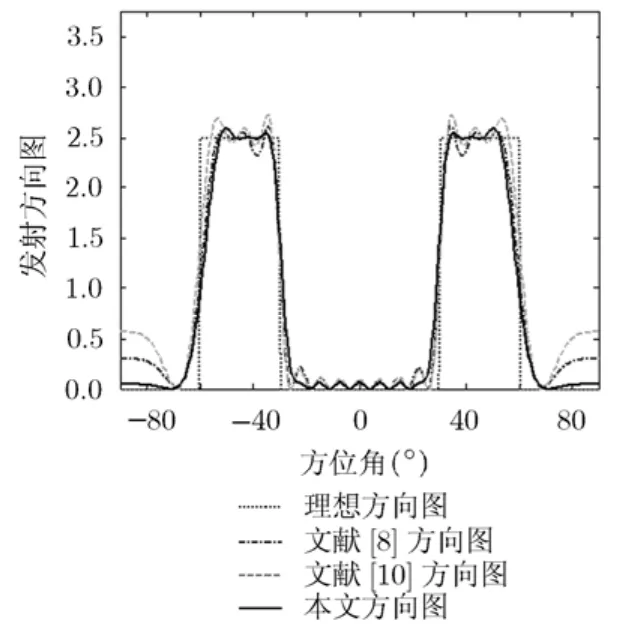
图4 对两个矩形方向图合成的实际发射方向图

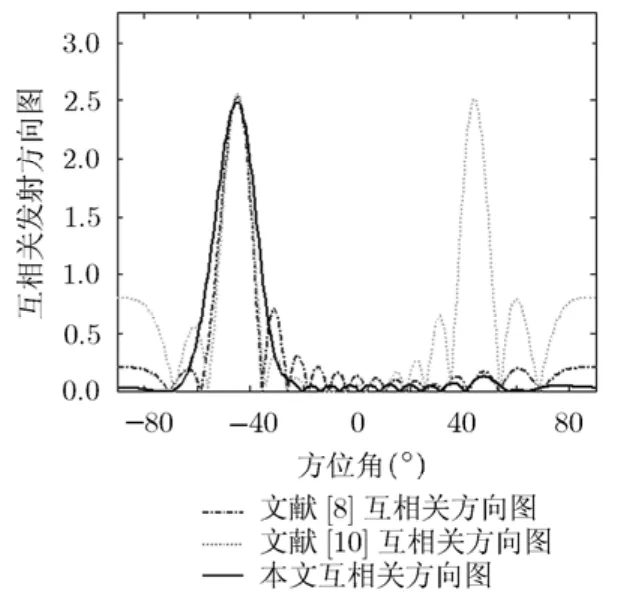
图5 -45°方向与其它方位角的互相关方向图

6 结束语

本文在集中式 MIMO阵列的任意发射方向图可以由一组基波束合成的基础上，提出利用基于二阶锥优化方法的主瓣宽度约束条件下最低旁瓣波束形成方法，构造出一组具有较低旁瓣的基波束，然后根据计算出的基波束比例系数合成实际的发射方向图。由仿真实验表明，该方法综合出的实际发射方向图更加逼近理想方向图，且具有旁瓣级低、相互干扰程度小的优点。

表1 计算时间随阵元数增加的变化(s)

[1]Li J and Stoica P.MIMO Radar Signal Processing[M].1st Ed,New York: Wiley,2009: 1-6.

[2]Li Wen-hua,Chen Gen-she,Blasch E,et al..Cognitive MIMO sonar based robust target detection for harbor and maritime surveillance applications[C].Aerospace Conference,Big Sky,MT,March 7-14,2009: 1-9.

[3]Fuhrmann D R,Browning J P,and Rangaswamy M.Signaling strategies for the hybrid MIMO phased-array radar[J].IEEE J.Selected Topics in Signal Processing,2010,4(1): 66-78.

[4]Ahmed S,Thompson J S,and Mulgrew B,et al..Fast computations of constant envelope waveforms for MIMO radar transmit beampattern[C].2010 IEEE,Radar Conference,Washington DC,May 10-14,2010: 458-463.

[5]Fuhrmann D R and San Antonio G S.Transmit beamforming for MIMO radar systems using partial signal correlation[C].The 38th Asilomar Conference on Signals,Systems,and Computers,Pacific Grove,CA,Nov.7-10,2004: 295-299.

[6]Fuhrmann D R and San Antonio G S.Transmit beamforming for MIMO radar systems using signal cross-correlation[J].IEEE Transactions on Aerospace and Electronic Systems,2008,44(1): 171-186.

[7]Li J,Xu L,Stoica P,et al..Range compression and waveform optimization for MIMO radar: a Cramér–Rao bound based study[J].IEEE Transactions on Signal Processing,2008,56(1): 218-232.

[8]胡亮兵,刘宏伟,杨晓超,等.集中式 MIMO 雷达发射方向图快速设计方法[J].电子与信息学报,2010,32(2): 481-484.Hu Liang-bing,Liu Hong-wei and Yang Xiao-chao,et al..Fast transmit beampattern synthesis for MIMO radar with collocated antennas[J].Journal of Electronics＆InformationTechnology,2010,32(2): 481-484.

[9]鄢社锋,马远良,孙超.基于二阶锥规划的任意传感器阵列时域恒定束宽波束形成[J].声学学报,2005,30(4): 309-316.Yan She-feng,Ma Yuan-liang,and Sun Chao.Beampattern optimization for sensor arrays of arbitrary geometry and element direetivity[J].Acta Acustica,2005,30(4): 309-316.

[10]Aittomaki T and Koivunen V.Low-complexity method for transmit beamforming in MIMO radars[C].Proceedings of IEEE International Conference on Acoustics,Speech and Signal Processing,Honolulu,HI,Apr.2007,Vol.2: 305-308.