基于压缩感知的双通道SAR地面运动目标检测方法研究
王伟伟 廖桂生 朱圣棋
(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
1 引言
双通道机载/星载合成孔径雷达(SAR)系统作用距离远,覆盖范围广,能够全天时地获取观测场景的静态和动态信息。与单通道SAR系统相比,多通道SAR系统具有更为理想的主瓣杂波抑制能力,能够有效检测地面慢速目标,因此在军事领域具有重要研究意义。
目前基于双通道SAR系统的运动目标检测方法主要有相位中心偏置天线(DPCA)技术[1,2]和沿航迹干涉(ATI)技术[3,4]等。基于图像域的杂波抑制方法需要首先对多个通道的回波数据分别进行SAR成像处理,而传统成像方法由于均受到奈奎斯特采样定理限制,从而给高分辨、大场景观测的A/D转换和数据存储传输系统带来沉重负担。近年来,稀疏信号处理技术得到迅速发展,Candes等人[5,6]给出了将稀疏线性回归等价转化为优化问题的充分条件(RIP条件)。Donoho等人[7,8]首次提出压缩感知的概念,为信号稀疏采样下的准确重建提供了重要理论依据。目前压缩感知技术已引起雷达领域科研人员的普遍关注,国内外已发表许多基于压缩感知技术的雷达成像及运动目标检测的相关文献[9-14]。在雷达成像方面,文献[9]提出了基于压缩感知技术的ISAR成像方法,该方法只需发射与接收少量脉冲,即使在较低信噪比情况下,仍可取得较高的成像质量;文献[12]运用压缩感知技术对某海滨场景进行SAR成像,在降采样50%数据条件下,实现了无模糊的SAR成像。在运动目标检测方面,文献[14]针对空时处理体制雷达研究基于压缩感知技术的运动目标检测方法,只对待检测距离门数据进行处理,无须估计协方差矩阵,因此非常有利于非均匀环境下的运动目标检测。
本文针对双通道SAR-GMTI系统,提出一种基于压缩感知技术的地面运动目标检测方法(本文简称CS算法)。该方法针对方位降采样的双通道回波数据,利用压缩感知技术实现SAR成像,并通过DPCA技术进行杂波抑制,从而最终实现地面运动目标检测。首先详细分析了基于CS算法的运动目标重构模型,从理论上分析了算法利用双通道降采样数据进行杂波抑制的可行性。并通过公式推导和仿真实验证明了运动参数对基于CS算法的目标成像的影响。仿真与实测数据实验证明了本文算法的有效性。
2 双通道雷达稀疏回波数据模型
图1为双通道SAR运动目标斜距与载机平台运动的关系示意图,其中va和vc分别表示方位向速度和距离向速度,aa和ac分别表示方位向加速度和距离向加速度;tm表示方位慢时间,ti为方位向的第i次采样时刻,Δti为方位向第i+1次采样与第i次采样之间的时间间隔;对于正侧视阵雷达斜视角为零,RB和R(tm)分别表示目标与载机的最近斜距和瞬时斜距;v为载机速度,d表示通道1和通道2的间距。由图1所示与传统沿方位向等周期发射与接收脉冲方式不同,本文方法由通道1沿方位向随机发射脉冲,通道1与通道2同时接收脉冲,则目标与两个通道间的瞬时斜距可近似表示为
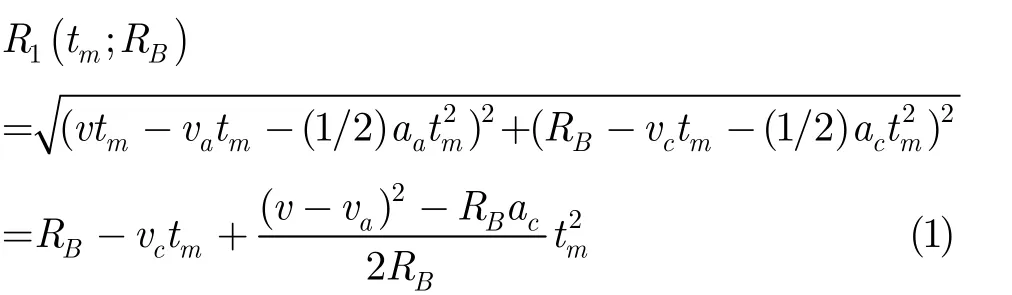
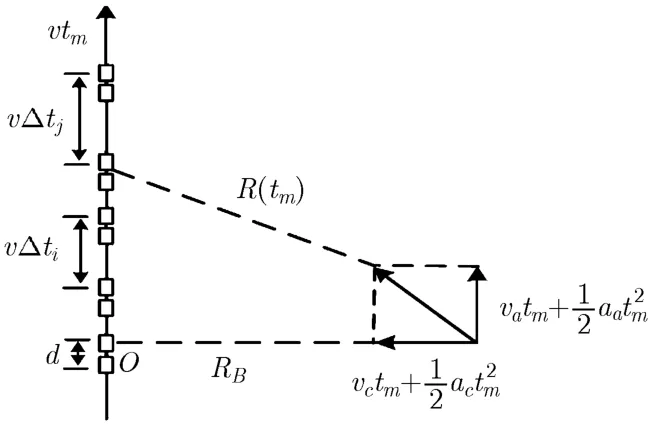
图1斜距平面SAR 数据接收示意图

假设总的合成孔径时间T0内共随机发射与接收M个脉冲,则以总合成孔径时间内的中心时刻作为慢时间的原点,由图1可知方位向慢时间tm满足
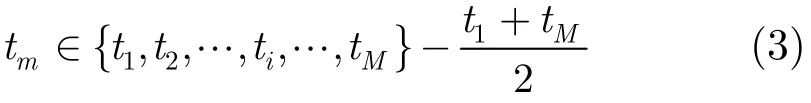
对于通道1经接收回波解调后,单个点目标的基频信号可以表示成复数形式。

其中t为距离向快时间,γ为发射信号调频率,σ为目标复散射系数,G1(tm)通道1的增益,c为光速,λ为载波波长,wr(t)为雷达线性调频(LFM)信号的窗函数,wa(tm)为方位窗函数。对于通道2由于只接收信号,因此经回波解调后,基频信号可表示为s2(t,tm)
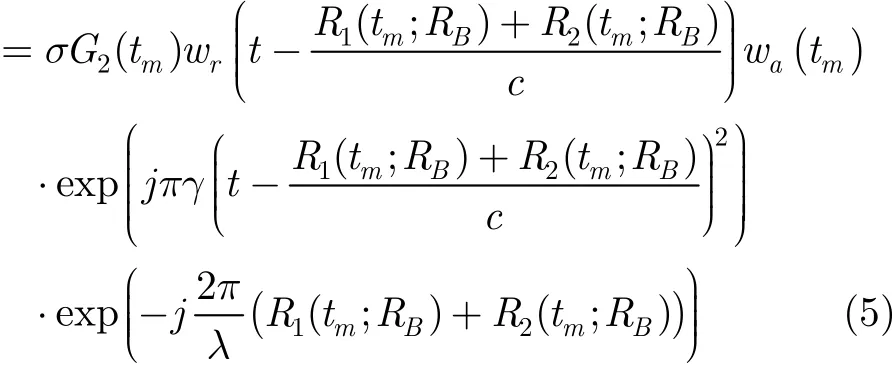
其中G2(tm)为通道2的增益。由式(4),式(5)可知,随机稀疏采样与传统采样方式的回波数据模型具有完全相同的结构形式,所不同的只是沿方位向相邻脉冲间的时间间隔是随机的。
3 基于压缩感知的地面运动目标检测方法(CS算法)
针对雷达接收的回波数据,首先运用匹配滤波方法进行距离向脉冲压缩处理,则得到通道1信号形式为

其中Δfr为发射线性调频信号的带宽,B为距离压缩后的总增益;fdc为多普勒中心,γm(RB)为多普勒调频率,理想情况下静止目标的回波数据fdc=0,对于运动目标由式(1)可知。由式(6)可以看出,目标的距离向速度可能会导致包络的越距离单元走动,在雷达分辨率与目标的距离向速度较低情况下,目标包络的距离走动可以忽略。假设某距离单元沿方位向在总的合成孔径时间T0内最多可分辨N0个散射点,则对接收回波进行距离向脉压后的信号可表示为
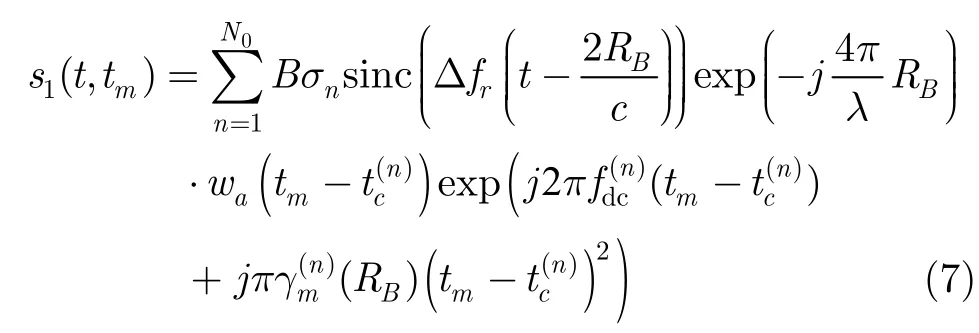
则式(7)简化为

因此根据式(8)雷达回波数据构建矩阵为
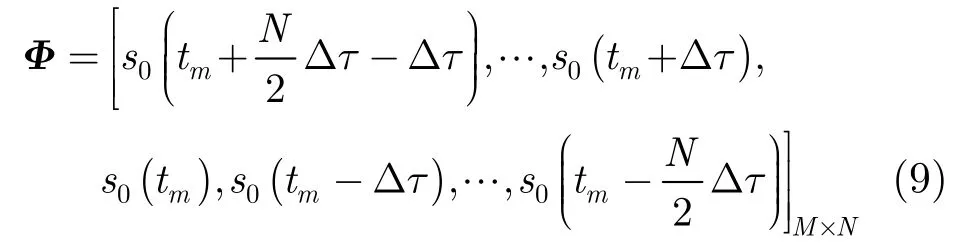
由于运动目标的运动参数是未知的,且对于正侧视阵在理想情况下杂波的多普勒中心fdc=0,令s0(tm-iΔτ)满足

其中取γm(RB)=-2v2/(λRB),wa(tm-iΔτ)为窗函数且满足

其中T1为一个全孔径的时间。而Δτ取值大小与方位向分辨率密切相关,一般情况下可取Δτ等于或略小于1/Δfa(Δfa为全采样条件下的多普勒带宽),N取大于 (T0+T1)/Δτ的偶数,且一般情况下M<<N,令则由式(8)可知,雷达回波信号可表示为式(12)的形式:
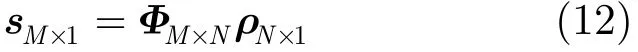
其中sM×1为距离向脉冲压缩后的回波数据,ΦM×N为观测矩阵,与采样方式有关,ρN×1即为某距离单元场景的复图像。由于式(12)为欠定方程组,因此存在无穷多个可行解。而近年来由Candes等学者提出的压缩感知理论给出了求解式(12)问题的充分条件与求解方法。根据压缩感知理论如果式(12)中ρN×1满足稀疏性(即ρN×1中的元素只有少量非零值或大系数),并且矩阵ΦM×N满足限制等距属性(RIP)条件,则可通过求解式(13)最小l1范数解重构方位向复图像ρN×1[15]。
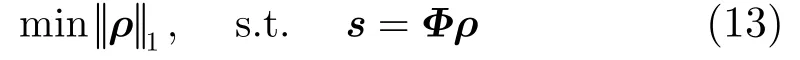
考虑存在噪声情况,式(13)可转化为

其中ε与噪声水平有关。需要指出的是一般情况下成像场景的空间分布不具备稀疏性,因此可能导致部分弱散射点不能准确重构,考虑到弱杂波散射点对运动目标检测影响相对较小,只要能够保证运动目标的散射系数能够准确重构,则场景散射系数的重构误差就不会对运动目标检测性能造成大的影响。为便于分析,首先考虑目标只存在距离向速度vc的情况,则由式(8)-式(10)可以求得由通道1回波数据重构的沿方位向第i个散射点的散射系数为

由式(6)可知,对通道2回波数据进行稀疏成像,并与通道1进行时间校准后,沿方位向重构第i个散射点的散射系数为


由式(17)可知,对于静止杂波不存在距离向速度,因此可以被对消掉。而运动目标由于存在距离向速度,不会被完全消掉,从而实现了杂波抑制与运动目标检测。以上只考虑目标存在距离向速度的情况,而当目标存在方位速度与距离向加速度时,会导致目标回波多普勒调频率与所构建冗余字典ΦM×N中的调频率相比出现偏差,从而会导致目标方位向散焦,该问题将在4.2节中进行详细讨论。
4 仿真数据实验及算法影响因素分析
4.1 基于CS算法的稀疏运动目标检测实验
为验证算法的成像性能及有效性,本节对两个通道的点目标仿真数据进行稀疏运动目标检测实验,仿真数据系统参数如表1所示。实验在距离向RB=5000 m处,设置3个静止的杂波散射点,其坐标分别设置为(5000,-20),(5000,0),(5000,20),并具有相同的散射系数幅度。实验同时在(5000,0)处设置一个运动目标,其距离向速度vc为0.4 m/s,后向散射系数幅度设为静止杂波的3/10。实验中采样数据量为满足奈奎斯特采样定理条件下所需最低数据量的1/3。首先对通道1和通道2数据分别进行距离向脉冲压缩,然后通过求解式(14)实现方位聚焦,仿真实验中取。图2(a),2(b)分别显示了通道1和通道2的稀疏成像结果,其中重构的静止杂波散射点分别标注为1,2,3,运动目标标注为4。由图2可以看出稀疏采样条件下CS算法对两个通道均能够较好的实现方位聚焦,不会出现方位模糊,但是两幅图像沿方位向相差1个像素点,经时间校准并补偿掉通道间的固定相位差后,由通道1与通道2相减即可实现杂波抑制和运动目标检测。图2(c)显示了杂波抑制后的CS图像,由图2(c)可以看出3个强杂波散射点基本被消除,而目标散射系数尚有较大剩余,因此证明了 CS算法的有效性。需要指出的是由于方位采样的随机性,导致每次实验获取的样本可能不同,但是通过多次实验表明,在采样相同数据量的情况下,每次实验的杂波抑制效果差别不大,在第5节的实测数据实验中也验证了这一点。

表1 仿真数据雷达系统参数
4.2 运动参数对CS算法目标成像的影响分析
由图2(a)可以看出,与传统RD算法相同,CS算法运动目标成像位置(标注为 4)与其真实位置(标注为2的杂波散射点)相比发生方位向偏移,大约向右偏移8个像素点。本节主要分析运动参数对目标成像的影响。首先考虑距离向速度对运动目标成像的影响,假设在(RB,x0)处存在一个运动目标,距离向速度和加速度分别为vc,ac,方位向速度为va。则经距离向脉冲压缩后某距离门的目标回波为


图2 基于CS算法的双通道成像与杂波抑制


以上分析了目标距离向速度对目标成像的影响,下面主要分析目标方位向速度和距离向加速度对成像的影响。通过第3节分析已知,目标的方位速度与距离加速度主要影响目标回波信号的多普勒调频率。为便于分析假设此时目标的距离向速度为0,并且目标的方位坐标x0=0,此时距离脉冲压缩后的目标回波可表示为
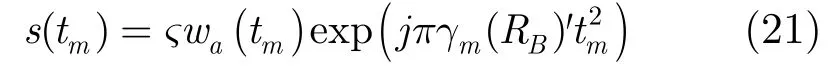
目标回波可由冗余字典中的原子线性表示为


5 基于CS算法SAR-GMTI实测数据实验
为验证本文算法的有效性,对实测双通道SAR数据进行处理,并与传统基于RD算法成像的SARGMTI方法进行比较。雷达工作在X波段,采用正侧视一发多收体制,平台速度为 120 m/s,场景中心斜距为6000 m,发射信号带宽为40 MHz。图4显示了沿方位向随机采样80%原始数据下,基于CS算法的 SAR图像(如图4(a)所示)与杂波抑制后的场景图像(如图4(b)所示),由图4可以看出运用本文提出的 CS算法对降采样的原始数据进行处理,能够有效实现方位聚焦,具有良好的杂波抑制性能,能够清晰地分辨6个运动目标。而此时对于采样相同数据的RD算法成像,沿方位向出现较大栅瓣,图像方位聚焦很差,经通道间图像配准与杂波抑制后,尚存在较大的剩余杂波,此时已很难有效进行运动目标检测 (如图5所示)。
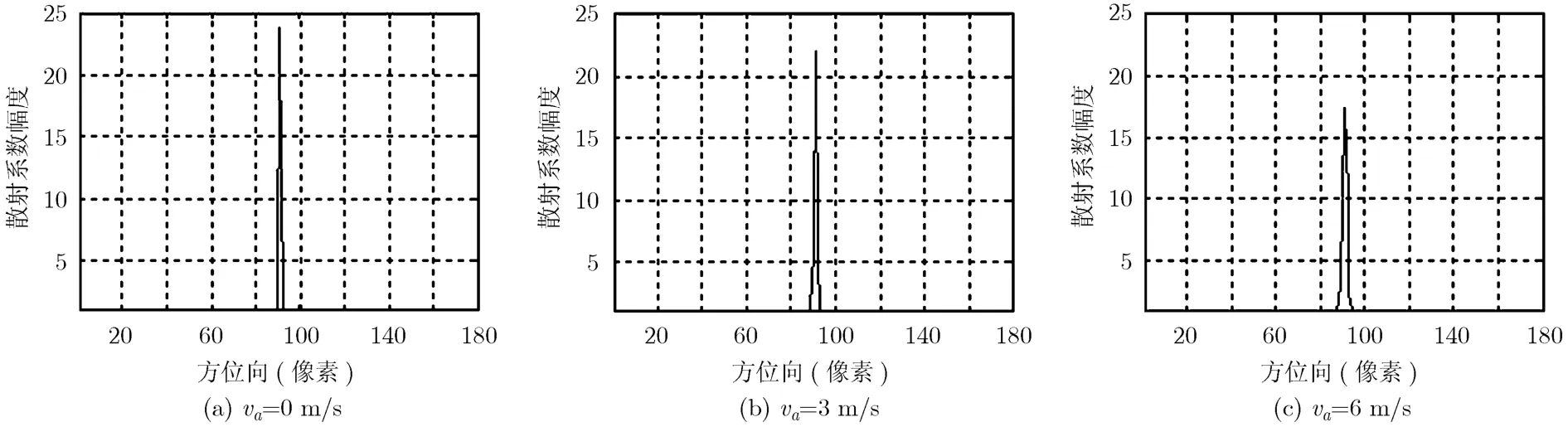
图3 多普勒调频率偏差对运动目标成像的影响

图4 80%原始数据的CS算法成像与杂波抑制
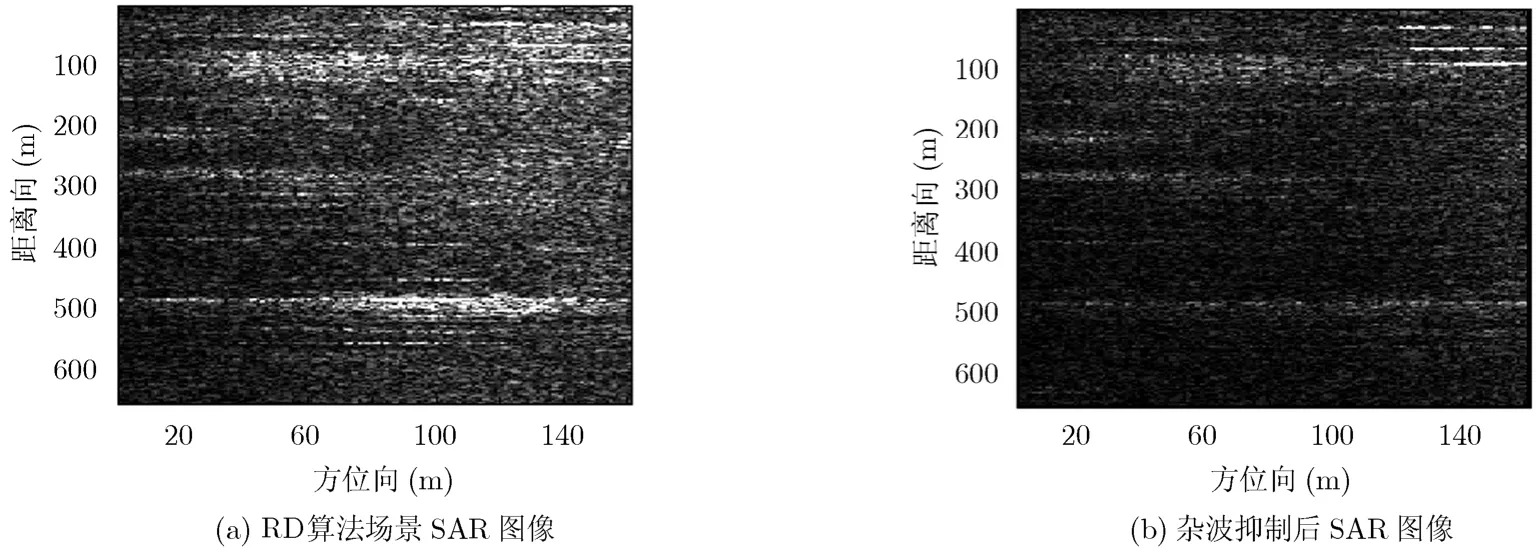
图5 80%原始数据的RD算法成像与杂波抑制
下面通过实验分析采样数据量对运动目标检测性能的影响,首先定义改善因子IF为 I F=SCNRout/SCNRin,图6标注了在不同采样数据量的条件下,经CS算法杂波抑制后,6个目标的改善因子。由图6可以看出随着采样数据量的减少,目标的改善因子逐渐降低,当采样数据量降至原始数据的50%时,改善因子急速下降,此时杂波抑制性能严重下降,主要原因是随着采样数据的减少,基于 CS算法的重构误差逐渐加大,由于重构误差具有一定的随机性,导致两个通道间的图像相关性变差,从而影响了杂波抑制性能。但是当采样数据为原始数据60%以上时,改善因子降低缓慢,60%采样数据比100%采样数据的改善因子大约降低1 dB至2 dB,以上实测数据实验证明本文方法在方位数据降采样情况下,仍具有较好的有效性。

图6 不同采样数据量下的改善因子比较
6 结束语
本文提出一种基于稀疏重构的双通道 SAR运动目标检测方法。该方法通过沿方位向随机稀疏采样的方式获得原始数据,距离向通过匹配滤波实现距离聚焦,并利用压缩感知技术实现方位向聚焦。本文详细分析了基于CS算法的运动目标重构模型,从理论上分析了算法利用双通道稀疏采样数据进行杂波抑制的可行性,并通过公式推导与仿真实验分析了运动参数对稀疏运动目标成像的影响。仿真与实测数据实验验证了算法的有效性。但是应当指出,随着采样数据的减少,基于 CS算法的运动目标检测性能会有所下降,造成该问题的主要原因在于成像场景散射点的空间分布稀疏性不够,在采样数据量较少的情况下会产生较大的重组误差,因此场景散射系数的稀疏性表示是一个需要进一步研究的难题。
[1]Wang H S C.Mainlobe clutter cancellation by DPCA for space-based radars[C].IEEE Aerospace Applications Conference Digest,Crested Butte,USA,Feb.1991:1-10.
[2]郑明洁,杨汝良.基于DPCA和干涉技术的SAR动目标检测[J].电子与信息学报,2003,25(11):1525-1530.Zheng Ming-jie and Yang Ru-liang.SAR moving targets detection based on dpca and interferometric processing[J].Journal of Electronic&Information Technology,2003,25(11):1525-1530.
[3]Pascazio V,Schirinzi V,and Farina A.Moving target detection by along-track interferometry[C].International Geoscience and Remote Sensing Symposium (IGARSS),Sydney,AUS,2001:3024-3026.
[4]Sikaneta I and Gierull C H.Ground moving target detection for along-track interferometric SAR data[C].IEEEAerospace Conference,Big Sky,USA,March,2004:2227-2235.
[5]Candes E J,Romberg J,and Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J].IEEETransactionson Information Theory,2006,52(2):489-509.
[6]Candes E J and Tao T.Near optimal signal recovery from random projections:universal encoding strategies?[J].IEEE Transactions on Information Theory,2006,52(12):5406-5425.
[7]Donoho D L,Elad M,and Temlyakov V N.Stable recovery of sparse overcomplete representations in the presence of noise[J].IEEE Transactions on Information Theory,2006,52(1):6-18.
[8]Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[9]Zhang Lei,Xing Meng-dao and Qiu Cheng-wei.Resolution enhancement for inversed synthetic aperture radar imaging under low SNR via improved compressive sensing[J].IEEE Transactions on Geoscience and Remote Sensing,2010,48(10):3824-3838.
[10]Huang Q,Qu L L,Wu B H,et al..UWB through-wall imaging based on compressive sensing[J].IEEE Transactions on Geoscience and Remote Sensing,2010,48(3):1408-1415.
[11]Lee C P,Ertin E,Parter J T,et al..Sparsity and compressed sensing in radar imaging[J].Proceedings of the IEEE,2010,98(6):1006-1020.
[12]Alonso M T,Lopez-Dekker P,and Mallorqui J J.A novel strategy for radar imaging based on compressive sensing[J].IEEE Transactions on Geoscience and Remote Sensing,2010,48(12):4285-4295.
[13]谢晓春,张云华.基于压缩感知的二维雷达成像算法[J].电子与信息学报,2010,32(5):1234-1238.Xie Xiao-chun and Zhang Yun-hua.2D radar imaging scheme based on compressive sensing technique[J].Journal of Electronic&Information Technology,2010,32(5):1234-1238.
[14]Selesnick I W,Unnikrishna Pillai S,et al..Angle-Doppler processing using sparse regularization[C].IEEE International Conference on Acoustic,Speech and Signal Processing,Dallas,USA,June,2010:2750-2753.
[15]Candes E J and Wakin M B.An introduction to compressive sampling[J].IEEE Signal Processing Magazine,2008,25(2):21-30.

