基于压缩感知的无线传感器网络多目标定位算法

何风行 余志军 刘海涛

①(中国科学院上海微系统与信息技术研究所 上海 200050)

②(无锡物联网产业研究院 无锡 214135)

1 引言

压缩感知理论自2006年正式提出以来[1,2]，在信号处理、通信、WSN等领域中的应用迅速成为学术热点。WSN主要特点是传感器节点的能量、计算能力、通信能力受限，而融合中心有相对强大的计算能力，能量不受限。基于压缩感知的系统特点是：传感器节点直接采样少量数据，同时完成采样和压缩，不需要基于香农-乃奎斯特定理进行大量、高速采样再额外运行复杂的压缩算法。这使得传感器节点变得简单、廉价，付出的代价是信号恢复时的重构算法运算量较大，而信号重构是在融合中心进行，融合中心没有能量、计算能力的苛刻限制。压缩感知的这种“天然特点”是为WSN“量身定制”的。

定位是WSN的支撑技术，WSN采集的信息中包含位置信息才能和物理世界对应，具有实际意义[3]。基于接收信号强度(RSS)的定位技术相比基于到达时间差(TDOA)，到达时间(TOA)，到达角度(AOA)等定位技术，具有成本低廉、无需多余硬件、容易获取等特点，取得广泛应用。近年来将稀疏变换、压缩感知应用于 WSN定位问题研究成为学术热点。文献[4]用稀疏变换研究定位问题，不足之处是算法的复杂度太高。文献[5]用压缩感知研究WSN的定位问题，它把 WSN目标定位问题转变为压缩感知问题，这种方法的不足之处在于每个传感节点都需要有一个定位字典(localization dictionary)，并且对目标在网格中的位置做了限定。文献[6]用压缩感知的方法研究了WSN目标定位问题，把WSN多目标定位问题转换为K个稀疏度为1的N维向量重构问题。不足之处在于 WSN需要传输的数据没有能进一步“压缩”，对于M个传感节点，K个目标的情况，需要传送M×K个传感数据。对于目标不在网格中心，该文采用的方法是把目标位置估计为候选定位结果集的中心，这是一种粗略的估计方法，会带来估计误差。

本文将WSN的基于RSS的定位问题转换为压缩感知问题，给出了明确的系统模型和工作方式，该方法大大降低了系统的通信开销，与文献[6]中的方法相比，通信开销从M×K减少到M。对于目标不在网格中心的情况提出了采用迭代回溯的压缩感知算法，显著提高了定位精度。仿真结果显示本文提出的方法具有较好的定位效果。

2 系统模型

系统模型如图1所示。设需要定位的区域为一方形区域，将此方形区域划分为N个网格。此区域中随机布设M个传感器，每个传感器的位置为已知。在整个区域中有K个目标(不要求K为已知量)。这是一个基于网格的目标定位问题，通过传感器接收到的信号强度确定目标处于N个网格中的哪些位置。

系统的工作方式如下：每个目标周期性发射信号，发送周期为T，目标之间相互独立，不要求同步。传感器周期性地收集信号，收集周期也为T，将该周期内收到的信号强度值做累加，周期时间片结束后，每个传感器将累加结果发送给融合中心。融合中心运行压缩感知定位算法，计算出目标处于N个网格中的哪些位置。

第m个传感器(1 ≤m≤M)和第n个网格(1≤n≤N)中的目标的欧式距离为

式(1)中，xm和ym为第m个传感器的坐标，xn和yn为第n个网格中目标的坐标。

无线信号强度的衰落受障碍物遮挡、多径传播等环境因素影响较大。大量实验统计结果表明，平均接收信号强度与信号传输距离之间的函数关系为[3]

图1 采用压缩感知的WSN多目标定位系统模型

设第n个网格中的目标发出的信号到第m个传感器处衰减后，变为

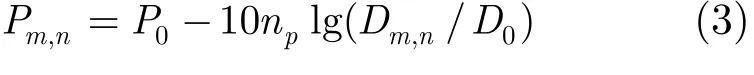
对噪声的处理方法是对传感器的测量结果叠加高斯白噪声。

3 压缩感知算法

压缩感知算法的一般过程为：已知测量矩阵Φ∈RM×N(M＜ ＜N)和某未知信号X∈RN在采用该测量矩阵时的线性测量值Y∈RM：

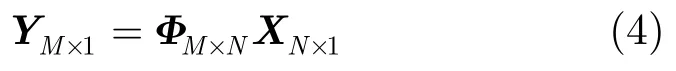
Y也可以看作信号X在测量矩阵Φ下的线性投影。压缩感知主要解决的问题就是由测量结果Y重构信号X。显然，由于X的维数远远大于Y的维数，这是一个欠定线性方程组求解问题，有无穷多解。然而压缩感知理论证明，如果信号X是K稀疏的，并且Y与Φ满足一定条件，信号X可以由测量值Y通过求解l1范数最小的最优化问题精确重构[1,2]：

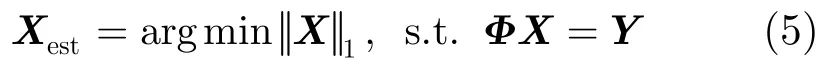
下面讨论压缩感知算法如何应用于 WSN的多目标定位。先分析目标位于网格中心的特殊情况，然后分析目标位于任意位置的一般情形。

(1)目标位于网格中心 将目标在网格中的位置限定为网格中心，位于第n个网格中目标的坐标为(xn,yn)。

测量矩阵Φ∈RM×N(M＜ ＜N)中的元素φm,n为第m个传感器接收到的位于第n个网格中目标的信号强度：

系统的压缩采样过程可用式(7)描述。

式(7)中xn=0 或1(1 ≤n≤N)，当第n个网格中有目标时xn=1 ，否则xn=0 。目标的总个数为K个，显然，N维向量X的稀疏度为K。传感器的测量结果Y为测量矩阵与稀疏向量X的乘积，其物理意义就是ym(1 ≤m≤M)为每个周期T内第m个传感器收到的多个目标信号强度之和。

式(7)简记为

这样，WSN的基于接收信号强度(RSS)的多目标定位问题转换为根据M个测量结果，重构N维稀疏向量的压缩感知问题。可以运用l1范数最小的最优化算法求出问题的解。

测量矩阵Φ的生成有两种办法：一种方法是根据采用的信号衰减模型生成测量矩阵，另一种方法是根据实际测试结果得到测量矩阵。本文采用的是前一种方法。信号的重构结果和测量矩阵有很大关系，当测量矩阵满足约束等距性条件(RIP)时信号可以得到精确重构，RIP条件是信号能够精确重构的充分条件而非必要条件[7,8]。文献[7]指出，X是稀疏度为K的N维向量，对X进行M次随机测量，如果满足式(9)，则可以通过求解l1范数最小的凸优化问题，由式(5)以压倒性的概率精确重构X。

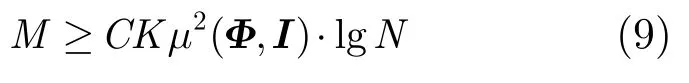
式(9)中，C为正的常数，μ(Φ,I)为矩阵Φ和单位矩阵I的互相关系数(mutual coherence)。矩阵的互相关系数μ(Φ,Ψ)表征了两个N×N单位正交矩阵Φ和Ψ的相关性：

式(10)中，和ψj分别为Φ和Ψ的第k行和第j列，可得

对于本例，由于信号X本身就是稀疏信号，所以Ψ=I，有

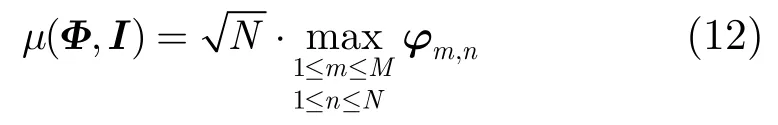
将矩阵Φ和Ψ限定为正交矩阵对压缩感知不是必须的，只是简化分析过程。由以上分析可得，需要的测量次数即传感器数量M，和目标个数K、测量矩阵和单位矩阵的互相关系数、网格划分数量N有关。 m axφm,n取决于传感器和划分的网格中心之间的最短距离。因此，布设的传感器最好和网格中心保持较大的距离，这样测量矩阵中的值就比较平均，每个测量结果的权重大致相同，可以取得较好的定位结果。如果测量矩阵中的个别值极大，对应个别传感器的权重很大，削弱其他传感器的测量结果的作用，将使得定位结果变差。

(2)目标位置任意 将目标的位置限定在网格中心是很有局限性的，实际上目标可以在网格中的任何位置。

压缩感知主要包括两个阶段[1,2]：压缩测量阶段和重构阶段。压缩测量阶段中得到压缩采样结果Y。重构阶段为根据测量矩阵Φ和测量结果Y重构X的过程。压缩感知要求重构矩阵等于测量矩阵，一般可以通过两种方式实现[4,6]：(a)将测量矩阵传输到重构端；(b)测量矩阵采用某随机种子产生的伪随机矩阵，重构端已知该随机种子，从而得知测量矩阵。而在本系统中，测量矩阵是对目标信号强度进行测量的实际过程中形成的，因此融合中心得不到测量矩阵。如果把目标的位置估计为网格中心，可以根据式(6)构造出测量矩阵，但若采用该测量矩阵进行定位，除不能定位目标在网格中的具体位置，还产生虚假目标。

我们采用多分辨率分析(MRA)方法解决这个问题，采用迭代回溯法[9,10]使重构矩阵逐步趋近于实际的测量矩阵。算法的核心思想是：若某网格中可能存在目标，则对目标在该网格中的位置不断迭代，选择使重构误差最小时的目标位置。迭代回溯算法的示意图如图2所示，若某网格中可能有目标，初始估计目标的位置为网格的中心位置O，重构信号，计算重构误差，第1次迭代时，将目标的位置尝试调整为A,B,C,D(分别是 4个小正方形的中心)，分别重构信号，计算重构误差，选择A,B,C，D,O5个点中重构误差最小的点作为目标位置的估计。这样就把目标在该网格中的位置区域由以O为中心的大正方形区域缩小为以A,B,C,D,O其中之一点为中心的小正方形区域。然后可以继续进行迭代过程，进一步缩小目标所在区域范围。

设第n个网格中的目标位置 (X(n,1),Y(n,1))初值为网格中心(XGn,YGn)，网格宽度为G。

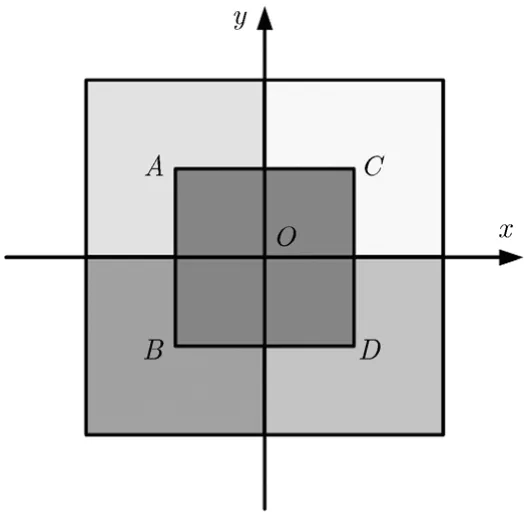
图2 迭代回溯算法示意图

第i次迭代时(i=1,2,3…)，目标的位置调整为

通过把目标的位置尝试调整为A,B,C,D，分别得出重构矩阵、重构信号，计算重构误差，目标位置取为A,B,C,D,O的重构误差最小的相应点位置。

由于N维向量X的元素的取值只有0和1(假设一个网格中不会有多个目标)，所以最理想的重构结果只有 0和 1。计算重构误差的目标函数选择为实际重构结果和理想重构结果的偏En为重构结果中的元素xn和理想结果的偏差：

重构的信号中绝大部分接近于 0，该值的大小也近似表示了该网格中存在目标的概率。因此可以只对大于某阈值的信号进行迭代回溯算法，降低算法的复杂度：

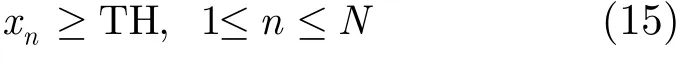
迭代回溯算法描述如下：

步骤2 生成重构矩阵Φ，运行重构算法得到重构结果X，计算重构误差。

步骤4 尝试调整目标位置至A,B,C,D，分别得到重构矩阵、重构信号、计算重构误差。取重构误差最小值所对应的点(A,B,C,D,O中之一)，接受为此次目标位置调整的结果。

本算法的步长调整类似于二分查找，每次迭代将把目标所在区域缩小为当前区域面积的1/4。理论上可以遍历该网格的任何位置，且不会超出该网格的范围。执行i次迭代后，目标可能在的位置缩小为网格面积的1/4i。

本迭代回溯算法的优点是定位精度不再受制于网格宽度G，在不增加网格数量N即问题维数的情况下，可以在网格中进一步精确定位，需要付出的代价是算法迭代次数的增加。在噪声情况下，定位结果差于Cramer-Rao界。关于本问题Cramer-Rao界可以参考文献[3,11]简单地推导出来，限于篇幅本文不再列出。

迭代算法的计算复杂度分析如下，设执行一次压缩感知重构算法的计算复杂度为O(1),X的所有元素中大于TH的元素有c×K个，则需要执行4c×K次压缩感知重构算法，计算复杂度为O(4c×K)。最好情况为O(4K)，最差为O(4N)。c的大小和TH的大小有密切的关系，仿真结果表明TH取为0.3左右有较好的效果，此时c约为1～2，执行i轮迭代回溯算法的计算复杂度为O(4c×K×i)。

实际情况中，重构偏差可能会趋于固定值，而不能任意小。造成该问题的原因有两个：TH的设定值和噪声情况。如果TH设定的值比较大，可能会使迭代回溯算法操作的点太少，无法调整目标在网格中的位置，致使该偏差只能趋于固定值。如果噪声比较大将影响重构信号的稀疏性，使得定位效果变差。

4 仿真结果

对本文所提出的基于压缩感知的定位算法在Matlab中进行了仿真验证，所采用的压缩感知重构算法为l1范数最小重构算法(BP)。定位区域设为50 m×50 m的方形区域。传感器布设在和网格中心1.5 m以外的区域。仿真参数的选取如表1所示。一般要求M＞2K，最好达到4K～6K，原信号可以得到较好的重构。仿真参数TH取为经验值0.3，如前文所述。采用的信号模型为：p0=-4 0 dBm,n0=2,d0=1。

表1 主要仿真数据参数

下面针对目标位于网格中心和位置任意的情况分别给出仿真结果。

(1)目标位于网格中心 图3为目标位于网格中心时，采用压缩感知算法的定位结果，共有9个目标。由图可以看出，在无噪声情况下得到了理想的定位效果。在SNR=20 dB和SNR=15 dB时的定位效果随噪声增大逐渐变差。

图4为通过200次蒙特卡罗实验结果，假设目标个数K为已知。目标正确关联的标准是：对目标的定位结果为目标实际所在的或相邻的网格。由图4(a)可以看出，随目标个数的增多即信号的稀疏度逐渐变差，平均定位误差逐渐变大。随着噪声的增大定位误差也会变大。由图4(b)可以看出，目标关联正确率随目标个数的增多、噪声的增大逐渐下降。图4表明在目标数量较少时压缩感知算法可以得到较高的定位精度，随着目标数量增加节省通信量的优势得以体现，但是定位精度逐渐下降。当K＞M/ 2时重构不出原信号，算法失效。

图3 目标位于网格中心时的压缩感知定位结果

(2)目标位置任意 图5为目标位置任意时的定位结果，共有7个目标。由图可以看出，在无噪声时，不采用迭代回溯算法会产生虚假目标，定位精度约为2 m。采用迭代回溯算法可以很大程度上抵消重构矩阵和测量矩阵的不同带来的影响，无虚假目标，定位精度小于 1 m，提高了 50%以上。在SNR=25 dB时产生虚假目标，定位精度变差。

和传统定位方法相比，压缩感知算法特点是降低了通信开销。传统工作方式中对K个目标进行定位需要传输数据量为M×K，压缩感知算法需要传输数据量为M，当K=20时只需上传原来5%数据量，适用于通信环境恶劣的 WSN网络。融合中心压缩感知重构 BP算法的复杂度为O(N3)。非压缩感知算法，比如LS (Least Squares)算法的复杂度为O(M3)。

5 结束语

本文提出了一种将压缩感知应用于 WSN多目标定位的方法，将 WSN的定位问题转换为压缩感知问题。本文提出的迭代回溯定位算法大大降低了系统的通信开销。仿真结果显示本方法具有较好的多目标定位效果。算法的不足是在噪声情况下性能较差，未来将开展对压缩感知定位算法优化的研究，提高系统在高噪声情况下的定位性能。

图4 目标位于网格中心时定位效果的评价指标

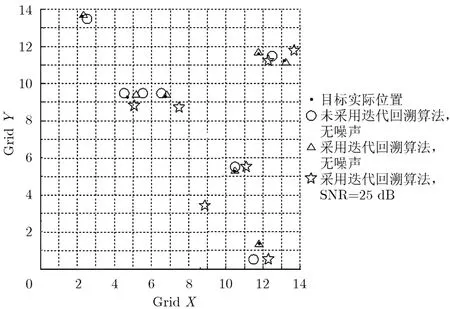
图5 目标位置任意时的压缩感知定位结果

[1]Donoho D.Compressed sensing[J].IEEE Transactions onInformation Theroy,2006,52(4)：1289-1306.

[2]Candès E,Romberg J,and Tao T.Robust uncertainty principles：exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory,2006,52(2)：489-509.

[3]Patwari N,Ash J N,Kyperountas S,et al..Locating the nodes：cooperative localization in wireless sensor networks[J].IEEE Signal Processing Magazine,2005,22(4)：54-69.

[4]Malioutov D,Cetin M,and Willsky A S.A sparse signal reconstruction perspective for source localization with sensor arrays[J].IEEE Transactions on Signal Processing,2005,53(8)：3010-3022.

[5]Cevher V,Duarte M F,and Baraniuk R G.Distributed target localization via spatial sparsity[C].Proceedings of the European Signal Processing Conference,Lausanne,Switzerland,Aug.25-29,2008：25-29.

[6]Feng Chen,Valaee S,and Tan Zhen-hui.Multiple target localization using compressive sensing[C].IEEE Global Communications Conference,Honolulu,HI,USA,Nov.30-Dec.4,2009：1-6.

[7]Candès E and Romberg J.Sparsity and incoherence in compressive sampling[J].Inverse Problems,2007,23(3)：969-985.

[8]Candès E and Plan Y.A probabilistic and RIPless theory of compressed sensing[J].IEEE Transactions on Information Theory,2011,57(11)：7235-7254.

[9]Blumensath T and Davies M E.Iterative hard thresholding for compressed sensing[J].Applied and Computational Harmonic Analysis,2009,27(3)：265-274.

[10]Dai Wei and Milenkovic O.Subspace pursuit for compressive sensing signal reconstruction[J].IEEE Transactions on Information Theory,2009,55(5)：2230-2249.

[11]Hossain A K M M and Soh W S.Cramer-Rao bound analysis of localization using signal strength difference as location fingerprint[C].IEEE Conference on Computer Communications,San Diego,CA,USA,Mar.15-19,2010：1-9.