基于小基高比的快速立体匹配方法

边继龙 门朝光 李 香

(哈尔滨工程大学计算机科学与技术学院 哈尔滨 150001)

1 引言

立体匹配是计算机视觉领域中的一个研究热点，它通过匹配两幅或者多幅同一场景在不同视角下的图像来获得对应点视差，然后根据三角测量原理计算出景物的深度信息。立体匹配方法可分为大基高比立体匹配方法和小基高比立体匹配方法。根据文献[1]的分类标准，大基高比立体匹配方法又可分为局部立体匹配方法[2-7]和全局立体匹配方法[8-11]。在局部立体匹配方法中，由于自适应权重[2-4]及其快速实现[5-7]的提出使局部算法具有了较高的匹配准确率和匹配效率。在全局立体匹配方法中，由于动态规划(Dynamic Programming)[8]、置信传播(Belief Propagation)[9]和图割(Graph Cut)[10,11]等全局优化算法的成功应用，使视差图的质量得到了明显的改善，并较好地解决了低纹理区域和遮挡像素的匹配。虽然大基高比立体匹配算法无论在速度方面还是在准确率方面都取得了一定的进展，但这些算法对立体像对中的遮挡、辐射差异和几何畸变的鲁棒性很差，经常导致大量的误匹配，致使计算结果难以满足实际应用的要求。为减弱上述因素对匹配的影响，小基高比条件下的立体匹配技术[12-17]应运而生。然而小基高比会造成深度精度的损失，为此在小基高比立体匹配中视差精度必须达到亚像素级别以弥补这部分损失。小基高比立体匹配方法的难点在于以下两个方面：(1)拒绝错误匹配以获得精确可靠的视差；(2)获得高精度的亚像素级视差。虽然目前的小基高比立体匹配方法[12-14]一定程度上解决了小基高比匹配中的可靠性问题，但该类算法的缺点在于匹配速度慢而且亚像素精度较低。

为了提高立体匹配效率同时获得高精度的亚像素级视差，本文提出一种快速的小基高比立体匹配方法。该方法主要有以下几点贡献：提出利用积分图像(integral image)加快自适应窗口和规范互相关度量的计算；根据可靠性约束进一步拒绝错误匹配以提高后续区域拟合的准确性；提出一种基于迭代二倍重采样的亚像素级匹配方法以补偿小基高比所造成的深度精度的损失。

2 算法框架

本文提出的快速小基高比立体匹配方法处理的是经极线校正的立体像对，并最终获得稠密的亚像素级视差图。该方法首先根据自适应窗口技术计算匹配窗口大小同时确定可信点和不可信点，再根据匹配窗口大小和规范互相关度量为可信点计算初始视差，然后利用可靠性约束进一步确定不可信点，在经过初始窗口选择和可信估计之后可以滤掉初始视差图中不可信视差。在获得可信视差的基础上，采用基于迭代二倍重采样的亚像素级匹配方法获得亚像素级视差，最后利用基于图分割的视差平面拟合方法获得稠密的亚像素级视差图。

3 算法的关键步骤及实现

3.1 局部匹配的数学分析

假设立体像对满足经典立体模型：

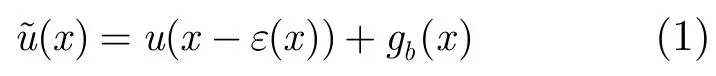
式中代表参考图像，u(x)代表匹配图像，ε(x)代表视差函数，gb(x)代表图像噪声。该模型仅在小基高比条件下才能满足，而且基高比越小模型越精确。基于小基高比的立体匹配方法[12]假设立体像对满足该模型并通过最大化支撑窗口间的互相关系数为参考图像中的每一点计算视差，其计算公式如下：

式中φx0=φ(x0-x)代表支撑窗口，代表内积，代表范数，τmu代表位移图像u(x-m)。

式(2)表明互相关函数的极值点所对应的视差值即为对应点视差，而且极值点即为导数为零的点，通过令连续互相关函数的导数为零可得

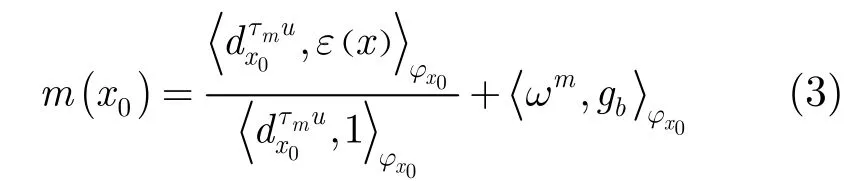
式中

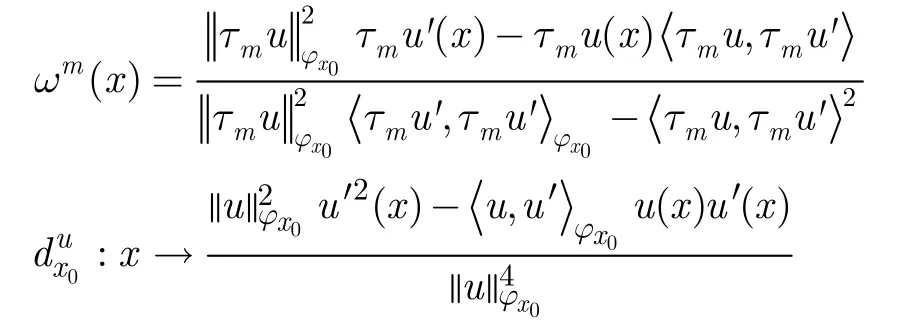
式(3)表明根据互相关系数计算的视差并不是该点的真实视差而是支撑窗口内所有真实视差的权重平均与图像噪声之和。依据式(3)匹配误差可分为两部分：一部分是由于支撑窗口违背了前视平坦假设造成的；另一部分是由图像噪声造成的。在匹配过程中，可通过减少第2部分噪声误差来提高算法的匹配精度。通过对匹配中第2部分噪声误差应用Schwarz不等式可得

根据式(4)第2部分噪声误差近似为

式(5)表示噪声所引起的匹配误差上界，在给定测量精度的情况下，可通过该式确定参考图像中每一点的匹配窗口大小。如果期望计算视差能足够精确地近似真实视差，应该选择满足误差精度的最小匹配窗口，其窗口选择公式为

式中α表示匹配误差精度。在窗口大小选择范围内满足式(6)的那些点称为可信点，否则称为不可信点。匹配过程中仅对可信点进行匹配，在获得可信点视差之后再推理获得那些不可信点视差。在实际应用中误差精度α的设定与所能接受的高程误差相关，例如，当基高比为0.01，允许高程误差为10 cm时，此时误差精度α应设置为0.01×10=0.1个像素左右。

3.2 积分图像加速

算法在实现过程中需要多次在矩形窗口上计算函数的权重和，若直接计算这些权重和，其复杂度同窗口大小成正比。为提高算法效率，需要加快这些求和运算。目前，实施快速求和运算的技术主要有以下几种方式：基于FFT的快速卷积技术、盒式滤波技术和积分图像技术，它们广泛地应用于立体匹配中的成本累积阶段。由于本文算法在匹配过程中每一点的支撑窗口大小都不同，因此积分图像[18]比较适合对本文算法进行加速。

为提高算法效率，本文首先将式(5)简化为

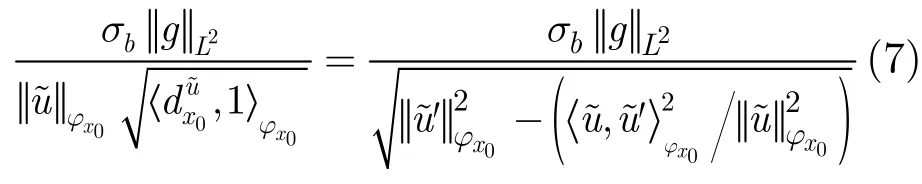
证明

根据式(7)，计算式(5)仅需要在矩形窗口上进行3次求和运算，再加上规范互相关函数式(2)的3次求和运算，窗口选择和成本计算一共需要6次求和运算。为了利用积分图像加快这些求和操作，本文使用常数函数作为支撑窗口函数。为此，式(7)的离散形式可表达为

相应的规范互相关系数的离散形式为

3.3 可信视差估计

虽然匹配过程仅处理那些在窗口选择阶段确定的可信点，但在匹配过程中还会存在一些误匹配。为进一步拒绝错误匹配提高后续区域拟合的准确性，本文对匹配过程施加了类似于文献[19]中的可靠性约束。

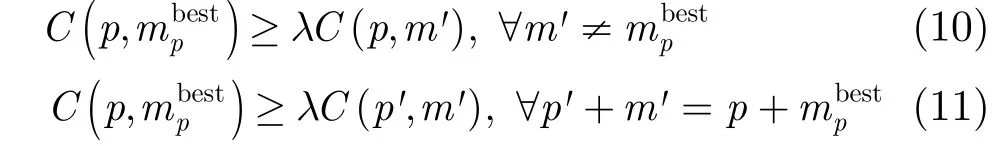
3.4 基于迭代二倍重采样的亚像素级匹配

小基高比立体匹配要获得与大基高比立体匹配相同的深度精度，则需要视差精确到1/m个像元精度，其中m为大基高比与小基高比的比值。为此，在小基高比立体匹配当中需要在整数级匹配之后加入亚像素级匹配以弥补小基高比对深度精度的影响。目前，亚像素级匹配方法主要包括图像重采样法[20]、拟合法[1]和相位法[15]。在这些方法当中，图像重采样法的亚像素精度最高，但该方法的计算复杂度较高。为了能获得高精度的亚像素级视差同时具有较高的匹配效率，本文提出一种基于迭代二倍重采样的亚像素级匹配方法。该方法每次迭代时仅对匹配图像中的支撑窗口进行二倍采样，然后在此分辨率上搜索最佳的亚像素级匹配位置。在下次迭代时，对最佳匹配位置的像素再次进行二倍采样，然后在这更高的分辨率上搜索最佳匹配位置。这个过程一直迭代直到达到想要的匹配精度为止。图1显示了 3×3窗口进行 3次迭代时的亚像素级匹配过程，匹配过程的每次迭代只是对最佳匹配点及其窗口内其它对应点进行二倍采样。

亚像素级匹配方法的详细过程如下：

(1)(x,y)的初始对应点为ql=(x+m(x,y),y)，其中，m(x,y)为整数视差，迭代次数k=1，位置偏移集为

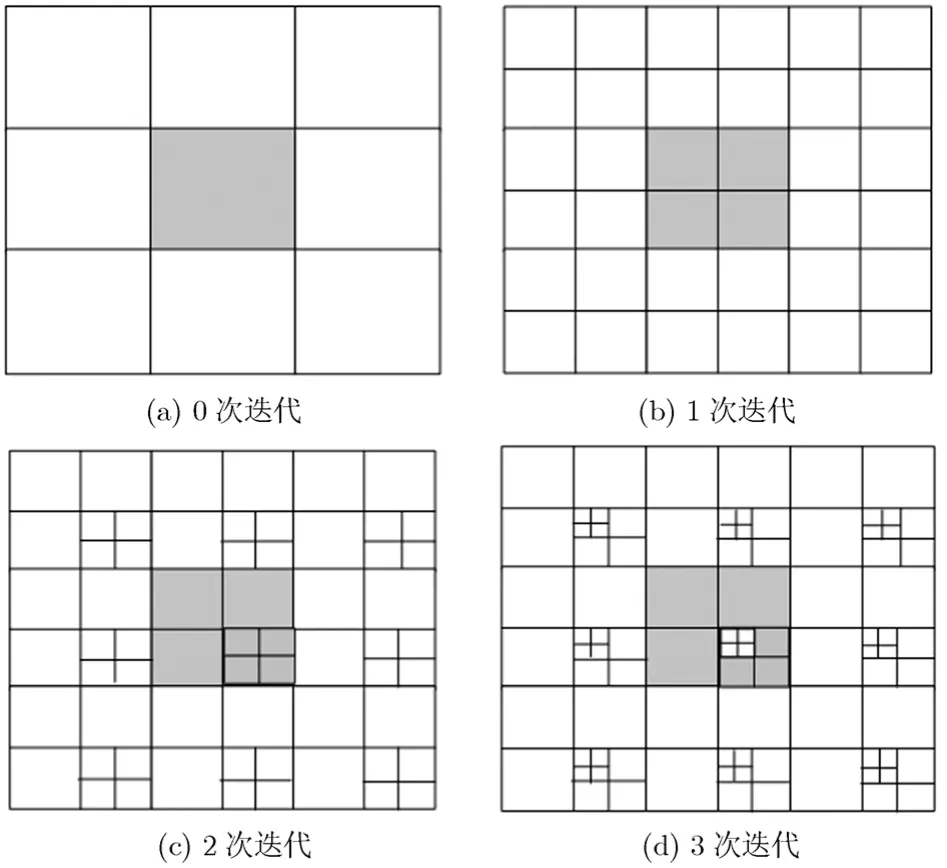
图1 亚像素匹配的迭代过程

以(x,y)为中心的参考窗口T(x,y)为

式中w表示窗口大小，wx,wy表示整型变量。

(2)根据对应点和窗口大小计算偏移窗口集。

(3)利用双线性插值计算匹配窗口Sr中每一元素的灰度值。

式中INT(⋅)表示取整操作，xp表示p点的横坐标，yp表示p点的纵坐标。

(4)根据规范互相关系数选择最优偏移量。

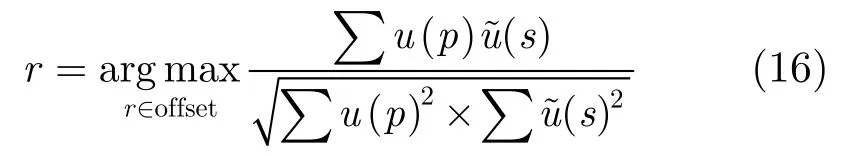
式中p∈Sr,s∈T(x,y)。

(5)计算亚像素级对应点位置。

(6)当k≤kmax转入步骤(2)继续迭代。

3.5 基于图分割的视差平面拟合

到目前为止，匹配算法获得的仅是稀疏的亚像素级视差图。为获得稠密视差图，本文采用了视差平面拟合法。该方法首先采用Mean Shift算法对参考图像进行过分割，然后根据每一分割块中的可信点的视差和坐标，利用最小二乘技术估计出视差平面参数：

式中(ai,bi,ci)是分割块Ri对应视差平面的法量，m代表像素(x,y)的视差。在获得平面参数后再根据式(18)计算那些不可信点的视差值进而可以获得稠密视差图。

4 实验结果

4.1 时间复杂度分析

现假设图像共有M个像素，窗口最大值为Wmax，最小值为Wmin，则直接实现窗口选择公式的时间复杂度为当使用积分图像对该公式加速时，计算窗口选择公式的时间复杂度仅为像的时间复杂度为O(M)，总共的时间复杂度为O(M)。

利用积分图像计算规范互相关函数式(9)也会节省大量的时间。计算式(9)需要计算1项建立积分图像需要的时间复杂度为O(M×d)，其中d为视差范围；第2,3项建立积分图像需要的时间复杂度仅为O(M)，总计时间复杂度为O(M×(d+1))。利用这些积分图像计算式(9)的时间复杂度仅为O(1)，一共需要的时间复杂度为O(M×(d+1))。直接实现式(9)的时间复杂度为O(M×W2(x)×d)，其中，W(x)表示每一点的窗口大小，该时间复杂度要远远大于O(M×(d+1))。

当亚像素精度精确到1/2k个像元时，本文提出的亚像素匹配方法的时间复杂度仅为O(9×K×W2(x)×M)，而图像重采样法的时间复杂度为O(2k×2k×W2(x)×M)。通过以上对比表明本文提出的小基高比立体匹配方法是一种快速的立体匹配方法，具有较高的匹配效率。

4.2匹配精度分析

为了验证本文算法的有效性，该实验采用了文献[12-14]实验中所使用的航空摄影像对Toulouse(如图2所示)，并与同类算法MARC[12],REGMARC[13],MERGE-MARC[14]的实验结果进行对比。实验采用vc++6.0编程，其运行环境为双核CPU2.2 GHz，内存为2 GB。

图2 Toulouse立体像对

Toulouse是一幅由 CNES提供的航空摄影像对，该立体像对的分辨率为 512×512，基高比约为0.045、地面分辨率为R=0.5，视差范围为[-2,2]，其获取时间间隔为20 min。由于获取时间间隔较长导致了立体像对中存在明显的运动和阴影移动，这增加了视差估计难度。

图3显示了同类算法[12-14]给出的实验结果和本文实验结果。图3(a)显示了真实视差图；图3(b)-3(d)分别显示了文献[12](MARC)，文献[13](REGMARC)和文献[14](MERGE-MARC)中给出的实验结果；图3(e)显示了在视差平面拟合过程中使用的图分割结果；图3(f)显示了参考图像中每一点的匹配窗口大小，图中的黑色表示不可信点，其它像素的灰度值代表该点的窗口大小，灰度值越大表示窗口越大，通过该图可以看出在物体边界处的匹配窗口相对较小，这可以有效防止“粘合”现象的发生；图3(g)显示了可信点视差，图中的黑色表示不可信点，这些不可信点一部分是在自适应窗口阶段产生的，另一部分则是在可信视差估计阶段产生的，这些不可信点视差将在后续的视差平面拟合中获得；图3(h)显示了本文算法的最终视差图。通过视差图的对比结果可以看出在实验结果图3(b)-3(d)中物体边缘处的视差参差不齐，未能很好地反应物体的形状，这会给3维重建带来较大的误差，然而本文实验结果图3(h)在物体边缘处的视差效果要明显优于其它算法，边缘处的视差非常整齐并清晰地反应出场景形状及细节信息。

利用均方根误差(Root-Mean-Squared Error,RMSE)对本文算法和文献[12-14]的算法进行了定量比较。表.1.显示了对比结果，第1列显示了待比较算法，第2列显示了可信点的RMSE，第3列显示了所有像素点的RMSE，第4列显示了算法的运行时间。从对比结果可以看出本文提出的小基高比算法不但具有较高的匹配精度，而且也具有较快的匹配速度。在实际应用中视差的匹配精度会受图像的采样频率、量化位数和噪声水平等因素的影响，不同条件的立体像对在视差精度上可能会存在较大的差异。

图3 实验结果对比

表1 均方根误差和运行时间

5 结论

本文提出一种快速的小基高比立体匹配方法，该方法在匹配过程中利用积分图像计算支撑窗口大小和规范互相关系数有效地提高了算法的匹配效率。在视差计算过程中加入可靠性约束提高了计算视差的准确性。在获得整数级视差后，利用基于迭代二倍重采样的亚像素级匹配方法获得高精度的亚像素级视差弥补了小基高比给深度重建带来的误差。最后采用了视差平面拟合方法估计不可信像素的视差值。实验结果表明本文提出的小基高比立体匹配方法不但可获得高精度的亚像素级视差以满足小基高比立体重建的要求，而且该方法的最大优点在于匹配速度与窗口大小无关。

[1]Scharstein D and Szeliski R.A taxonomy and evaluation of dense two-frame stereo correspondence algorithms[J].International Journal of Computer Vision,2002,47(1-3)：7-42.

[2]Yoon K J and Kweon S.Adaptive support-weight approach for correspondence search[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2006,28(4)：650-656.

[3]De-Maeztu L,Villanueva A,and Cabeza R.Stereo matching using gradient similarity and locally adaptive support-weight[J].Pattern Recognition Letters,2011,32(13)：1643-1651.

[4]Heo Y S,Lee K M,and Lee S U.Robust stereo matching using adaptive normalized cross-correlation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(4)：807-822.

[5]Li Li,Zhang Cai-ming,and Yan Hua.Cost aggregation strategy for stereo matching based on a generalized bilateral filter model[C].Proceedings of International Conference on Information Computing and Applications,Tangshan,China,2010：193-200.

[6]Richard C,Orr D,and Davies I,et al..Real-time spatiotemporal stereo matching using the dual-cross-bilateral grid[C].Proceedings of the 11th European Conference on Computer Vision Conference on Computer Vision,Crete,Greece,2010：510-523.

[7]丁菁汀,杜 歆,周文晖,等.基于 FPGA 的立体视觉匹配的高性能实现[J].电子与信息学报,2011,33(3)：597-603.Ding Jing-ting,Du Xin,and Zhou Wen-hui,et al..High performance implementation of stereo vision matching based on FPGA[J].Journal of Electronics＆InformationTechnology,2011,33(3)：597-603.

[8]Bobick A F and Intille S S.Large occlusions stereo[J].International Journal of Computer Vision,1999,33(3)：181-200.

[9]Sun Jian,Zheng Nan-ning,and Shum H Y.Stereo matching using belief propagation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2003,25(7)：787-800.

[10]Papadakis N and Caselles V.Multi-label depth estimation for graph cuts stereo problems[J].Journal of Mathematical Imaging and Vision,2010,38(1)：70-82.

[11]Komodakis N,Paragios N,and Tziritas G.MRF energy minimization and beyond via dual decomposition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(3)：531-552.

[12]Delon J and Rougé B.Small baseline stereovision[J].Journal of Mathematical Imaging and Vision,2007,28(3)：209-223.

[13]Facciolo G.Variational adhesion correction with image based regularization for digital elevation models[D].[Master dissertation],Universidad de la Republica Oriental del Uruguay,2005：37-49.

[14]Igual L,Preciozzi J,and Garrido L.Automatic low baseline stereo in urban areas[J].Inverse Problems and Imaging,2007,1(2)：319-348.

[15]Morgan G L K,Liu Jian-guo,and Yan Hong-shi.Precise subpixel disparity measurement from very narrow baseline stereo[J].IEEE Transactions on Geoscience and Remote Sensing,2010,48(9)：3424-3433.

[16]Sabater N,Blanchet G,and Moisan L,et al..Review of low-baseline stereo algorithms and benchmarks[C].Proceedings of Image and Signal Processing for Remote Sensing XVI,Toulouse,France,2010：1-12.

[17]Robin A,Moisan L,and Le Hegarat-Mascle S.An a-contrario approach for subpixel change detection in satellite imagery[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(11)：1977-1993.

[18]Veksler O.Fast variable window for stereo correspondence using integral images[C].Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition,Madison,USA,2003：556-561.

[19]Wei Yi-chen and Quan Long.Region-based progressive stereo matching[C].Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition,Washington,D.C.,USA,2004：106-113.

[20]黎俊,彭启民,范植华.亚像素级图像配准算法研究[J].中国图象图形学报,2007,13(11)：2070-2075.Li Jun,Peng Qi-min,and Fan Zhi-hua.A survey of sub-pixel image registration methods[J].Journal of Image and Graphics,2007,13(11)：2070-2075.