基于重尾噪声分布特性的多分类人脸识别方法

张如艳 王士同

①(江南大学物联网工程学院 无锡 214122)

②(江南大学数字媒体学院 无锡 214122)

1 引言

人脸识别技术自诞生之日起，因其操作简单，实现方便等特点而成为生物识别技术中应用最为广泛的方法之一。这些优点通常只有在比较理想的人脸图像中才能得到充分体现。但是在实际应用中，会有各种类型不确定的噪声，对人脸图像的质量和识别效果产生影响。

通常，噪声模型会被估计为高斯噪声，而研究发现，在工程应用中，噪声模型往往表现出非高斯性，即概率密度函数分布往往表现出较厚的尾部统计特性[1]，如合成孔径雷达图像中、海杂波的尖峰幅度分布情况，都呈现出很多幅度较大的噪声，此时的噪声已经不再是高斯噪声，而是重尾噪声。对于重尾噪声的研究和应用并不仅仅局限于海波、雷达等领域。人脸识别作为一种被广泛使用的模式识别方法，有必要将重尾噪声引入到人脸图像中，研究其分类识别算法，这对于研究人脸识别技术具有重要意义。

概率密度函数估计，考虑样本数据的实际分布情况，能够为贝叶斯分类提供有力工具。最大后验概率[2]把分类问题看成一个统计估计问题，根据其所属类别概率做出统计判断。t分布具有尖峰后尾的统计特性[3]，符合非高斯噪声模型特性。因此，文中将其结合，得到t分布下基于核函数的最大后验概率分类方法(T Kernel-based MaximumA Posteriori,TKMAP)，并验证其对含重尾噪声的人脸图像的识别效果。

2 重尾噪声模型

常用的噪声模型有椒盐噪声，乘性噪声，高斯噪声，重尾噪声等[4]。本文研究重尾噪声，重尾噪声分布模型有 Cauchy噪声，Erlang噪声，Laplace噪声，负指数噪声以及混合高斯噪声等。其概率密度函数的详细描述如下。

其中a＞0,b是正整数，均值为b/a，方差为b/a2。

(5)混合高斯噪声由高斯噪声获得，即若f1(x)是的概率密度函数，)的概率密度函数，则以+αf2(x)为概率密度函数的随机变量，即为混合高斯噪声。其中α为闪光频率，一般情况下，α很小，μ1=μ2且σ1≤σ2。

3 基于核函数的分布模型

3.1 核函数

在人脸识别中，样本数往往小于人脸维数，这就是小样本问题[5]。而基于核函数的方法只需要明确样本数目而非具体维数，所以，在很大程度上，解决了维数灾难的问题。

理论上，满足Mercer定理[6]的函数都可以作为核函数，目前常用的核函数有

(1)RBF(高斯径向)核函数：

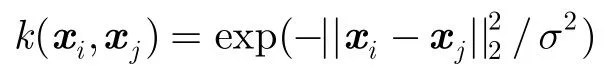
其中σ为尺度参数，σ在很大程度上影响着RBF核函数的性能。

RBF核函数是典型的局部性核函数，距离较远的样本对核函数的值影响较小。文献[7]表明，只要选择合适的σ，对于任意给定的样本集，RBF核函数可以对训练样本集做出正确分类。

其中c为常数，d为多项式阶数。当c=0,d=1时，多项式核函数变成线性核函数。

多项式核函数是典型的全局性核函数，较远的样本点对核函数的值有较大的影响。在d很大时，

(3)Sigmoid核函数：

其中scale和offset分别为尺度和衰减参数。

通常，Sigmoid只有在scale＞0和offset＜0时才适合做核函数，由于Sigmoid核函数没有特别的优势，因此一般不选择其作为核函数。

目前，核函数类型多数是由特定领域的专业知识以及经验来确定。核函数参数的确定，主要有试凑法和最优化方法[8]。人脸图像在加入重尾噪声后，其特征分布与原始人脸图像相比，发生了很大变化。RBF核函数作为一种局部性核函数，能够根据图像的局部特征，很好地进行平滑运算，分类性能好。所以本文采用RBF核函数，并根据试凑法确定其中的参数。

3.2 贝叶斯分类器

贝叶斯分类方法具有坚定的数学基础，它以Bayes理论为基础，以先验概率和条件概率密度函数为依托，是一种有指导的模式识别方法。与其他算法相比，贝叶斯分类器具有最小出错率[9]。其关键是确定样本数据的概率密度函数p(φ(x)|Ci)[10]。

假设m类样本数据为第i类数据个数。核空间中，贝叶斯分类器的设计为以下 3个步骤：

首先，计算类Ci的先验概率p(Ci)。通常，无法得到p(Ci)的精确值，故根据类Ci的样本比率估计[11]，即p(Ci)=Ni/N。

其次，利用如下的贝叶斯公式计算后验概率p(Ci|φ(x))。

最后，根据分类规则，如果p(Cw|φ(x))=则x∈Cw，选择具有最大后验概率的类Cw作为该样本所属的类别。

3.3 公式的核化形式

目前，概率密度估计主要有参数估计法和非参数估计法。文中选择参数估计法，利用t分布下的概率密度函数估计，采用最大似然方法，获得分类概率。

假定一组独立的p维数据 {x1,x2,…,xN}，多元t分布为t(μ,∑,v)。其中，μ是中心；∑是对称、正定的矩阵；v＞0是自由度，控制t分布的尾部形状。核空间中，t分布的类条件概率密度函数为

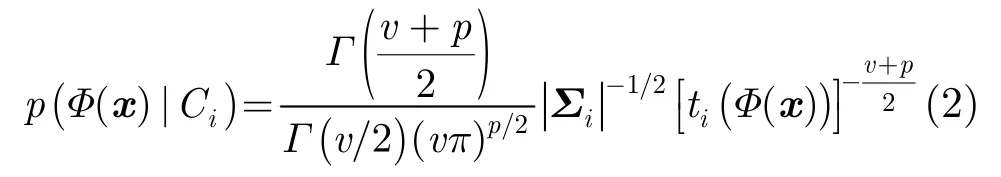
定义

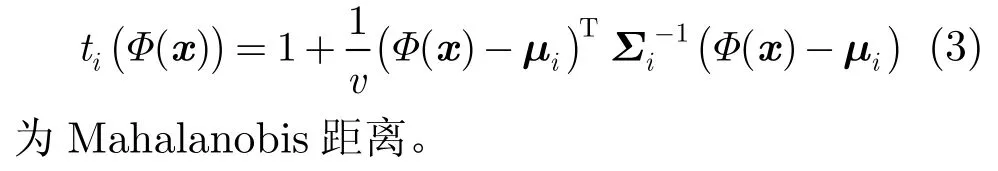
3.3.1 协方差矩阵规整化和对角化均值μi和协方差∑i的表达式为

从式(4)和式(5)中可以看到，∑i只与样本个数有关，而与其数据维数无关。因此，在小样本情况下，根据μi和∑i求得的均值和协方差是病态的，可以利用如下的规整化方法。

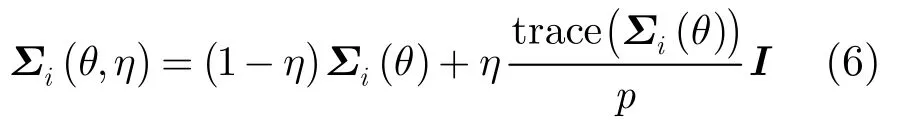
由于映射函数φ未知，故无法求出∑i。而由于∑i是对称、正定矩阵，可以将其对角化[12]为如下形式：

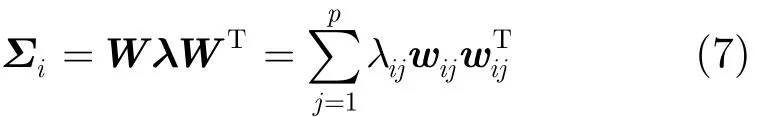
其中λij为∑i的第j个特征值，wij为与λij相对应的特征向量，∑i的特征值已经按照从大到小的顺序排列。

将∑i代入式(5)中，得到

3.3.2 Mahalanobis距离公式由于高维的人脸特征对人脸分类的作用并不等同，所以为减少时间复杂度，先进行降维处理。主成分分析(Principal Component Analysis,PCA)作为一种经典有效的降维方法，已经广泛的应用到人脸识别中[13]，其降维过程不考虑样本数据的类别属性，而是将全体数据作为一个整体，求得样本在投影方向上具有最大方差的特征。

借鉴PCA降维思想，但与PCA不同的是，文中并没有舍弃第k+1个以后的特征值，而是用第k+ 1 个特征值hi(k+1)代替第k+1个后的所有特征值，以减少能量的损失[14]。则式(8)变为

根据再生核理论，所有对应于λij≠ 0 的特征向量wij必存在于φ(x1),φ(x2),…,φ(xN)所张成的空间中。因此，wij可以用它们的线性组合来表示[15]，即存在系数αi(i=1,2,…,N)使

由协方差矩阵定义可知，一对特征值与特征向量{λij,wij}满足

由于特征向量之间是正交的，式(11)有如下变形

将式(7)和式(10)代入式(12)，得到λij为

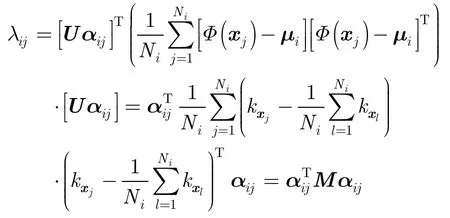
其中

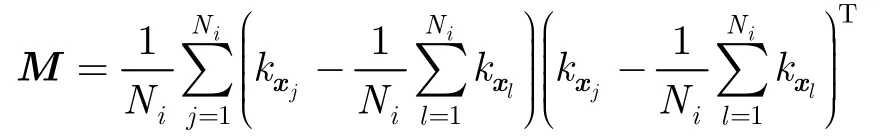
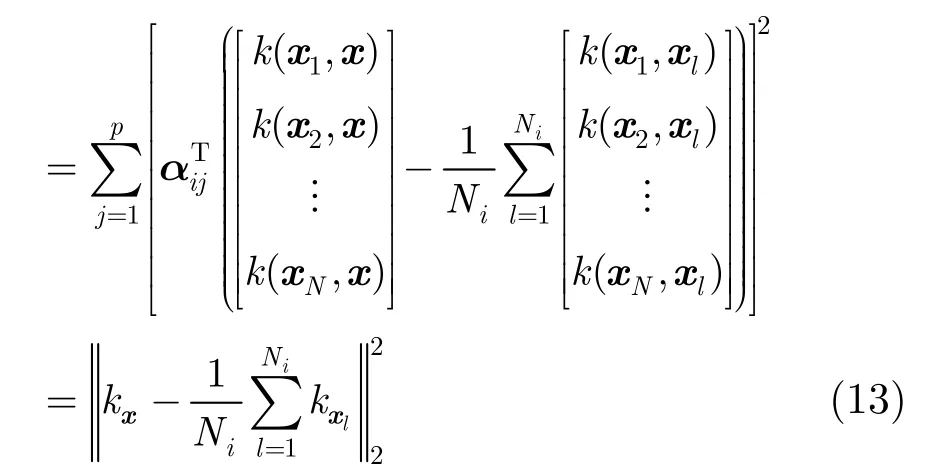
同理，得

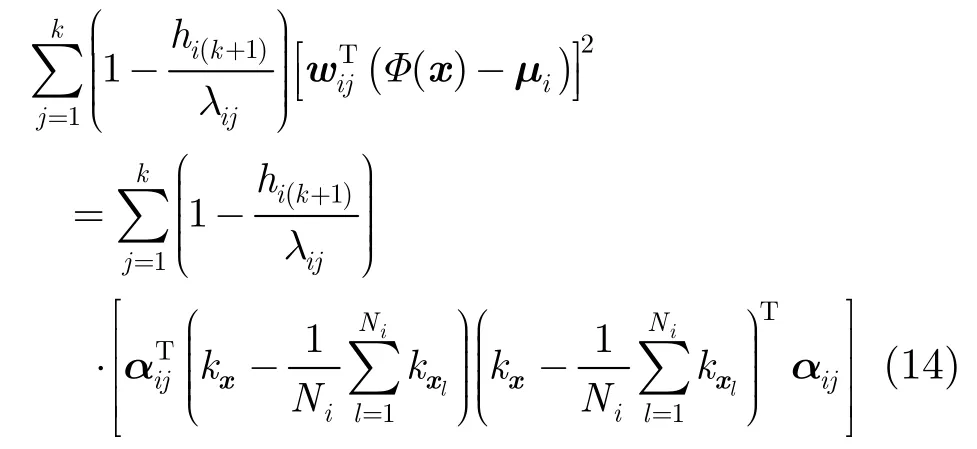
将式(13)和式(14)代入式(9)中，得

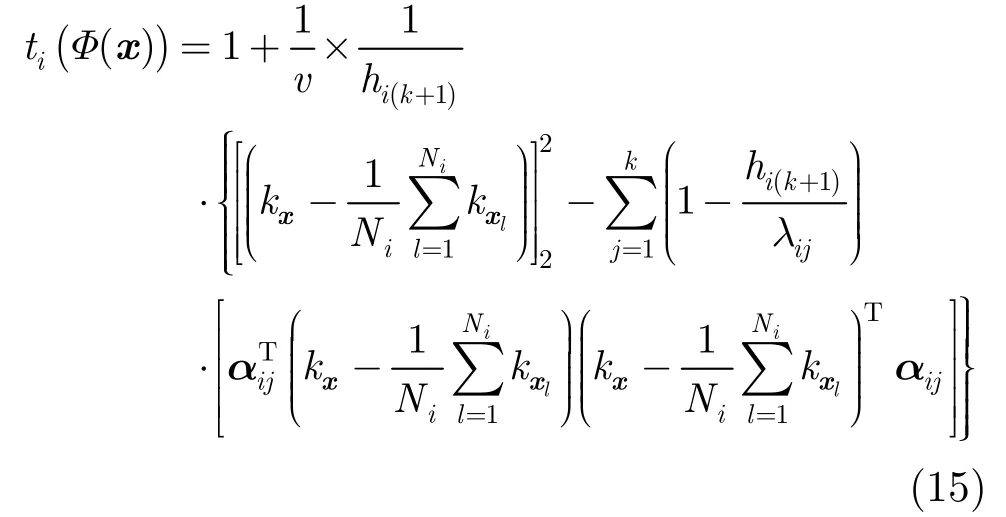
其中λij和αij是矩阵M的一对特征值与特征向量。

3.4 实验步骤

(1)分析5种重尾噪声分布模型，得到含重尾噪声的待识别人脸图像。根据含重尾噪声的人脸图像的特性，选择具有良好平滑性的RBF核函数。

(2)在核空间中，将t分布与核函数、贝叶斯公式相结合进行推导，得到 Mahalanobis距离ti(φ(x))。

(3)采用试凑法确定RBF核函数以及ti(φ(x))中的参数值。首先设定参数的初始值，然后根据实验结果不断调试参数值，直至得到比较满意的实验数值。

(4)根据贝叶斯分类方法，得到某一样本数据的类别可信度，由最大后验概率确定样本所属分类。

4 模拟实验及分析

实验在ORL和Yale数据集上进行。为了验证本文所提出的算法的分类性能，引入3种对比算法，Gauss分布下基于核函数的最大后验概率分类方法(Gaussian Kernel-based MaximumA Posteriori,GKMAP)，核主成分分析方法 (Kernel Principal Component Analysis,KPCA)和核Fisher判别方法(Kernel Fisher Discrimiant Analysis,KFDA)。

4.1 人脸数据集简介

ORL人脸数据集由40人，每人10幅112×92的图像组成，其中的人脸图像是正面图像，光照、姿态表情变化不是很大。Yale人脸数据集中共有15人，每人11幅图像，其中的图像拍摄环境较复杂，光照强度、姿态表情的变化比较大。为了降低时间复杂度，将ORL中的人脸图像大小归一化为53×64，将Yale中的人脸图像大小归一化为50×50，但并未做任何内容上的更改。图1和图2显示了ORL和Yale中的部分人脸图像。

图1 ORL中的部分人脸图像

图2 Yale中的部分人脸图像

在ORL和Yale中，分别添加5种类型的重尾噪声，在每种噪声中设置3种参数，从而得到同种噪声模型下，受污染程度不同的人脸图像，添加噪声后的某人脸图像如图3和图4所示。图3和图4中，从左到右的5列图像，分别为添加3种噪声参数的Cauchy噪声，Erlang噪声，Laplace噪声，负指数噪声和混合高斯噪声的人脸图像。

4.2 实验结果

经过反复实验，ORL和Yale中的参数值分别为，RBF核函数中的参数σ=15和σ=10，规整化参数θ=0 .01,η=0 .03和θ=0 .01,η=0.06，自由度参数v=5和v=3。

实验中，在ORL和Yale中随机选择2,3,4,5和6张人脸图像作为训练样本集，剩下的人脸图像作为测试样本集。限于文章篇幅，只列出ORL中添加Cauchy噪声的人脸图像的识别率，如表1所示，Yale中添加Erlang噪声的人脸图像的识别率，如表2所示，ORL和Yale中含其他4种重尾噪声的人脸图像识别率在4种算法中有类似的实验结果。实验结果为20次实验的平均值。

图3 ORL中含5种重尾噪声的人脸图像

图4 Yale中含5种重尾噪声的人脸图像

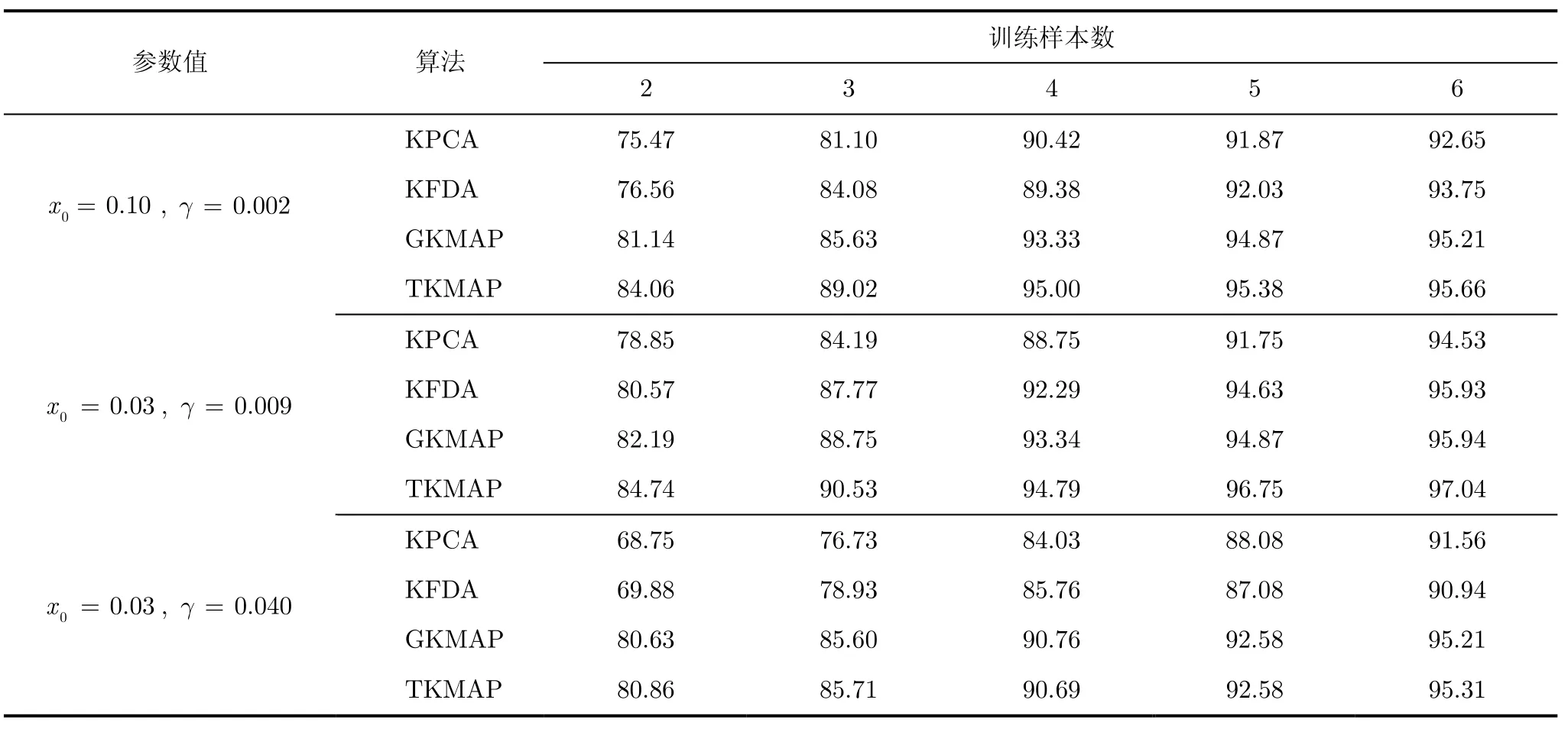
表1 ORL中含Cauchy噪声的人脸图像的识别率(%)

4.3 实验结果分析

从实验结果可以看到，随着训练样本数目的增加，4种人脸分类算法的识别率均有提高。在样本数目相同的前提下，前两种算法 KPCA和 KFDA的识别效果没有后两种算法 GKMAP和 TKMAP理想。这是因为，虽然核函数在一定程度上解决了小样本问题，但是其并没有考虑人脸图像的实际概率密度分布情况，而后两种算法在核函数的基础上，结合统计分布概念，能够比较合理地估计人脸图像的概率密度分布。

算法GKMAP和TKMAP的比较，识别精度上，第一，由于t分布对尖峰拖尾情况有比较好的适应性，故算法TKMAP比GKMAP的鲁棒性好。第二，当人脸图像中的噪声点比较少时，TKAMP比GKMAP的识别率高很多，而当噪声点比较多时，人脸特征变化较大，相应地概率密度函数的变化也很大，无法通过试凑法比较准确地确定其中的参数值，故两种方法的识别效果相差不大。复杂度上，由于 TKMAP需要不断调整参数v，所以比GKMAP耗时，但是由此换来了更好的实验效果。

5 结束语

本文将概率密度函数估计中的参数估计、核函数以及贝叶斯理论结合起来，提出t分布下的基于核函数的最大后验概率多分类方法TKMAP。该算法主要利用t分布能够比较好地适应样本数据的拖尾特性，进而能够对含重尾噪声的人脸图像的实际拖尾情况进行有效估计。实验结果证明，与其他3种算法相比，TKMAP在去除重尾噪声方面表现出了良好的抗噪能力。但在算法实现中也存在一些问题，例如如何根据含重尾噪声的人脸图像的拖尾情况，定量确定t分布中的自由度参数v，是一个值得深入研究的问题。

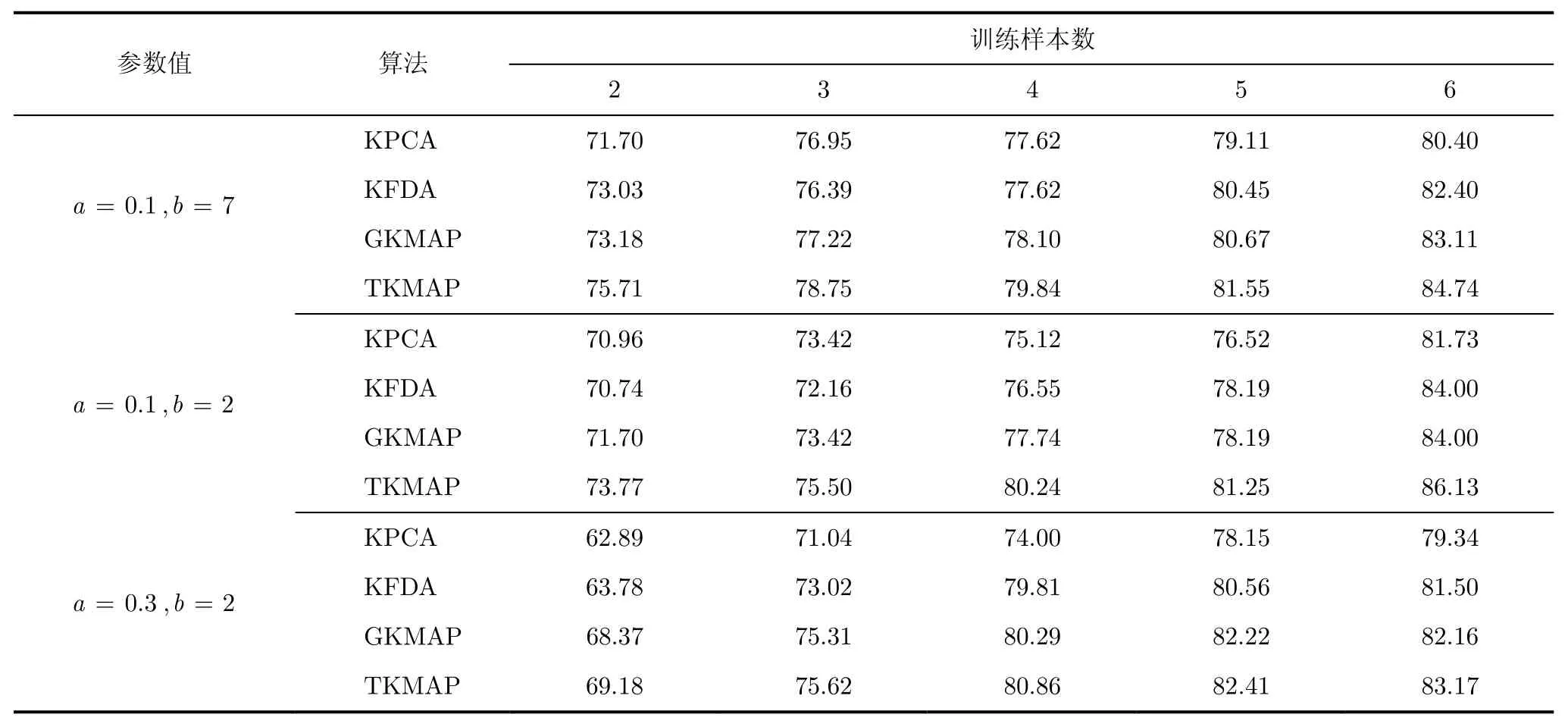
表2 Yale中含Erlang噪声的人脸图像的识别率(%)

[1]Mukherjee A and Sengupta A.Estimating the probability density function of a nonstationary non-Gaussian noise[J].IEEE Transactions on Industrial Electronics,2010,57(4)：1429-1435.

[2]Duda R O,Hart P E,and Stork D G.Pattern Classification[M].Wiley-Interscience Publication,2000：20-102.

[3]Wang Zhi-min and Song Qing.Robust curve clustering based on a multivariate t-distribution model[J].IEEE Transactions on Neural Networks,2010,21(12)：1976-1984.

[4]王桥.数字图像处理[M].第 1版,北京：科学出版社,2009：21-30.Wang Qiao.Digital Image Processing[M].First Edition,Beijing：Science Press,2009：21-30.

[5]楼宋江,张国印.零空间保局判别本征脸[J].电子与信息学报,2011,33(4)：962-966.Lou Song-jiang and Zhang Guo-yin.Null space locality preserving discriminant intrinsicface[J].Journalof Electronics＆Information Technology,2011,33(4)：962-966.

[6]John S T and Cristianini N.Kernel Methods for Pattern Analysis[M].Cambridge University Press,2004：289-325.

[7]褚蕾蕾,陈绥旭,周梦.计算智能的数学基础[M].北京：科学出版社,2002：105-110.Chu Lei-lei,Chen Sui-xu,and Zhou Meng.Mathematical Basis of Computation Intelligence[M].Beijing：Science Press,2002：105-110.

[8]刘向东,骆斌,陈兆乾.支持向量机最优模型选择的研究[J].计算机研究与发展,2005,42(2)：576-581.Liu Xiang-dong,Luo Bin,and Chen Zhao-qian.Optimal model selection for support vector machines[J].Journal of Computer Research and Development,2005,42(2)：576-581.

[9]张全新,郑建军,朱振东,等.贝叶斯分类器集成的增量学习方法[J].北京理工大学学报,2008,28(5)：397-400.Zhang Quan-xin,Zheng Jian-jun,Zhu Zhen-dong,et al..Increment learning algorithm based on Bayesian classifier integration[J].Transactions of Beijing Institute of Technology,2008,28(5)：397-400.

[10]Zhang Yan and Zhang Tao.Kernel-based Bayesian face recognition[C].2009 Fifth International Conference on Natural Computation,Tianjin,China,2009,7：568-572.

[11]钟桦,焦李成,侯鹏.基于非下采样Contourlet变换的视网膜分割[J].计算机学报,2011,34(3)：574-582.Zhong Hua,Jiao Li-cheng,and Hou Peng.Retial vessal segmentation using subsampled Contourlet transform[J].Chinese Journal of Computers,2011,34(3)：574-582.

[12]Ruiz A and Lopez-de Teruel P E.Nonlinear kernel-based statistical pattern analysis[J].IEEE Transactions on Neural Networks,2001,12(1)：16-32.

[13]Zhao Hai-tao,Yuen Pong-chi,and Kwok J T.A novel incremental principal component analysis and its application for face recognition[J].IEEE Transactions on Systems,Man,and Cybernetics,2006,36(4)：873-886.

[14]Xu Zeng-lin,Huang Kai-zhu,Zhu Jian-ke,et al..A novel kernel-based maximum a posteriori classification method[J].Neural Networks,2009,22(7)：977-987.

[15]Schölkopf B,Smola A,and Müller K R.Nonlinear component analysis as a kernel eigenvalue problem[J].Neural Computation,1998,10(5)：1299-1319.