未知信源数目的DOA估计方法

李鹏飞 钟子发 张 旻

(合肥电子工程学院309研究室 合肥 230037)

(安徽省电子制约技术重点实验室 合肥 230037)

1 引言

在现代电子战信号环境中，由于信号密度大，信号形式复杂，使得电子侦察中的信号处理任务越来越困难。对无线电测向提出了高精度、高分辨率、解相干信号等方面的要求。最经典的波达方向(DOA)估计方法是利用波束在空间扫描来确定目标的方向，但是它无法分辨两个很近的空间信号。以MUSIC(MUltiple SIgnal Classification)[1]算法为代表的空间谱估计方法突破了瑞利限，可以达到很高的精度。该类算法一般要求信源数目精确已知，当估计的信源数与真实信源数不一致时，会对信源方位的估计产生严重影响。同时在存在相干信号时，其性能严重下降，虽然可以通过空间平滑的方法进行解相干，但是阵列孔径损失严重。

信号稀疏分解作为一种新出现的信号分析思想，可以得到信号的一个非常简洁的表达(即稀疏表示：sparse representation)，已经在诸多应用领域体现出其优势[2-5]。阵列信号的空间谱并不是连续的，也就是说仅仅存在少数几个非零值分别代表着相应的空间方位。空间信号的这种稀疏特性，决定了我们可以用稀疏分解的方法进行DOA估计。利用稀疏分解的方法进行D O A估计具有以下的优点[6-10]：(1)具有很高的分辨率和估计精度；(2)不需要进行任何预处理，可以直接应用到相干信号上来；(3)对初始值的选择不是很敏感。利用快拍数据的稀疏分解进行DOA估计容易受到噪声的影响。Malioutov等人[10]提出了l1-SVD(l1norm Singular Value Decomposition)的方法进行DOA估计，即对阵列接收数据进行奇异值分解(SVD)，然后利用l1范数约束求解稀疏解得到目标的估计值。l1-SVD方法克服了快拍数据稀疏分解容易受到信号噪声影响的缺点，但是该方法需要已知信源数，当信源数过估计时，性能严重下降。

针对以上问题，本文提出了两种不需要估计信源数目的DOA估计方法。一种基于特征向量稀疏分解(Eigen Vector Sparse Decomposition,EV-SD)的DOA估计方法，采用协方差矩阵最大特征值对应的特征向量来代替阵列快拍数据作为稀疏分解向量，可以有效减少噪声及信号幅度跳变的影响，和l1-SVD算法相比不需要估计信源数目，增强了算法的鲁棒性。另一种基于协方差矩阵高阶幂稀疏分解(High Order Power Sparse Decomposition,HOPSD)的DOA估计方法。首先证明了阵列接收数据的协方差矩阵的高阶幂的列向量是所有信号方向矢量的线性组合，因此可以利用其列向量的组合建立DOA估计的稀疏模型。该方法避免了估计信号源数目和特征值分解。

2 数学模型

2.1 阵列信号的数学模型

假设来波方向为θi(i=1,…,p)的p个远场信号入射到M元天线阵列，t时刻第l个阵元的接收信号为

τli为第l阵元相对参考阵元的延迟，写成矢量形式为

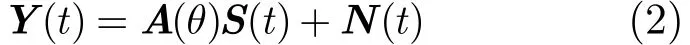
式中Y(t)为t时刻采集的M×1维的阵列快拍数据矢量；A(θ)为M×p维的阵列导向矢量矩阵，A(θ)=[a(θ1),a(θ2),…,a(θp)];S(t)为t时刻的p×1维的空间信号矢量；N(t)为M×1维的阵列噪声数据矢量；其中，导向矢量为

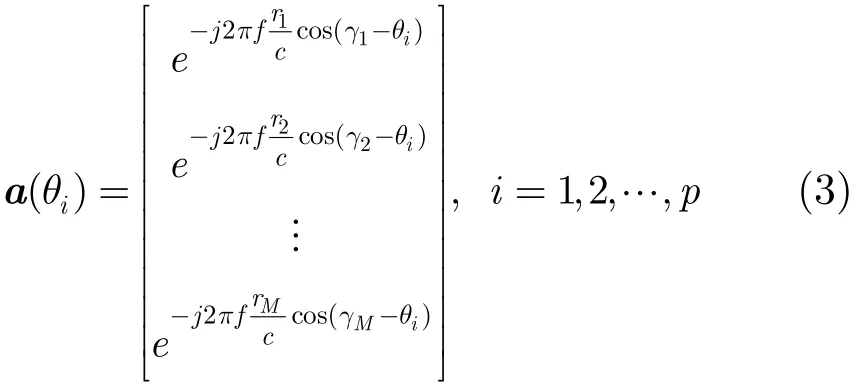
式中rl(l=1,2,…,M)为阵列参考点和阵元n距离，γl(l=1,2,…,M)为阵元l相对参考点的极坐标角度，c为电磁波传播的速度。

2.2基于稀疏表示的DOA估计模型

稀疏表示进行 DOA估计的主要思想是将信号的阵列流型矩阵扩展成一个过完备的冗余字典D，它包含了所有可能的源位置信息。令θ={θ1,θ2,…,θN}代表所有可能的源位置的一个采样集合，θn代表信号的到达角度(DOA)，方向矩阵A可扩展成如下的过完备字典：

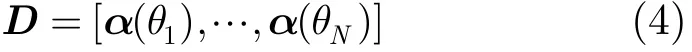
定义N×1的信号向量h={h1,h2,…,hN}，当且仅当源信号位于角度θn处，hn有非零值，其他分量均为零，可以得到DOA估计的稀疏模型：

利用基追踪(Basic Pursuit,BP)[11]等稀疏分解算法求得h，根据h中非零元素的位置可以得到信号的DOA。直接利用式(5)进行稀疏分解进行DOA估计，容易受到噪声的影响。文献[10]提出l1-SVD的方法进行DOA估计。即对式(2)阵列的接收数据采集多个快拍，然后对这些快拍数据进行奇异值分解，取其中的p个较大奇异值对应的奇异向量的线性组合作为式(5)待分解的向量Y。

3 未知信源数下的DOA估计方法

3.1基于阵列协方差矩阵特征向量稀疏分解的DOA估计方法(EV-SD算法)

l1-SVD方法需要估计信号源的数目，本文利用多快拍数据估计阵列输出的协方差矩阵，然后对协方差矩阵作特征值分解，利用最大特征值对应的特征向量作为待分解的数据向量，来实现 DOA估计，避免了估计信源数目。

多采样信号可以表示成如下形式：

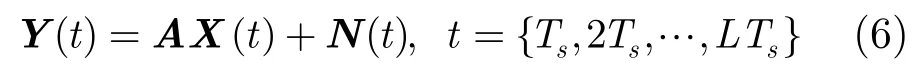
利用L个快拍数据得到阵列的协方差矩阵估计值。

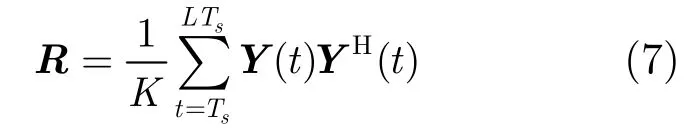
对R做特征值分解得

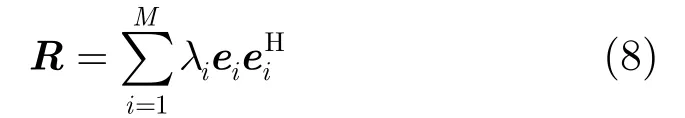
如果信号协方差矩阵的秩为K(K≤p)，假设噪声协方差矩阵RN为满秩矩阵，则有如下线性关系[12]：

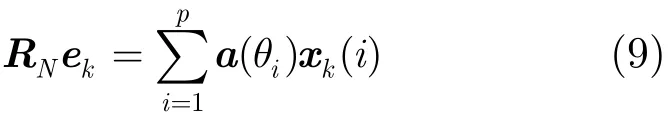
其中1≤k≤K,ek为特征矢量，xk(i)为线性组合因子。当噪声协方差矩阵为理想白噪声时，式(9)即简化为

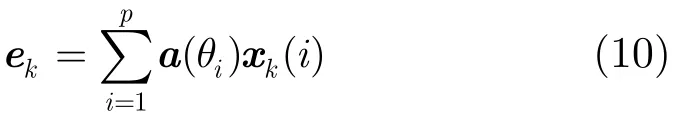
式(10)说明无论信号源是否相干，最大特征值对应的特征矢量是各信号源方向矢量的一个线性组合。令协方差矩阵的最大特征值为emax，则

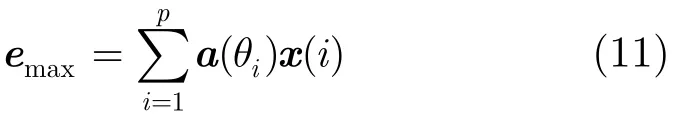
参照式(4)对a(θi)进行扩展，形成冗余字典D，得到特征向量的稀疏模型：

对式(12)进行稀疏分解得到h,h中非零元素的位置就代表了空间目标的方位信息。不同于基于快拍数据稀疏分解的 DOA估计方法，特征值分解减弱了噪声的影响，而选取最大特征值对应的特征向量进一步减弱了噪声的影响，因此本文方法在低信噪比情况下鲁棒性较好。

3.2 基于阵列协方差矩阵高阶幂稀疏分解的DOA估计方法(HOP-SD算法)

EV-SD方法虽然不需要估计信号源的数目，但是计算过程中的特征值分解计算量较大。因此本文提出一种不需要特征值分解和估计信号源数目的DOA估计方法。对阵列协方差矩阵R做特征值分解：

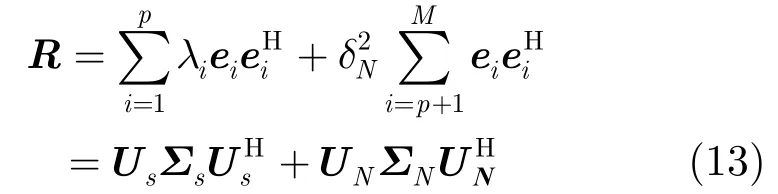
式中∑s为大特征值组成的对角阵，∑N为小特征值组成的对角阵。Us=[e1,e2,…,ep]为大特征值对应的信号子空间，UN=[ep+1,…,eM]为小特征值对应的噪声子空间(信号为独立信号时，p为信号个数；存在相干信号时，p为协方差矩阵的秩)。由式(13)可得

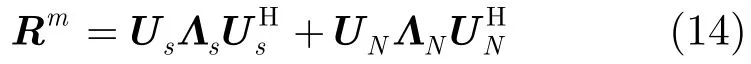
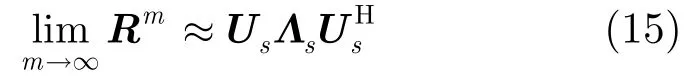
实际应用时，在一定信噪比条件下，m取有限整数就能获得很好的收敛性能。令Rm=[r1,r2,…,rM],rm为M×1维的列向量。根据式(15)，则

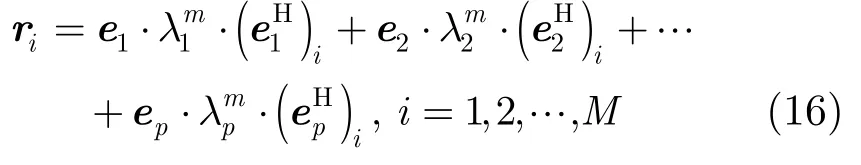
其中(·)i表示取向量的第i个元素。从式(16)可以看出，ri是所有大特征向量的线性组合。将协方差矩阵高阶幂的所有列向量相加，形成一个新的向量：

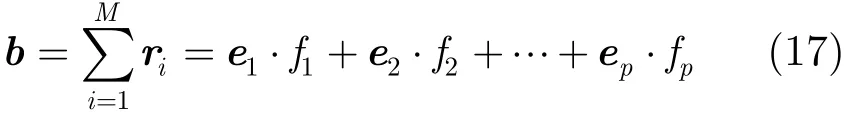
其中fi(i=1,2,…,p)代表组合系数。式(10)说明无论信号源是否相干，大特征值对应的特征矢量是所有信号方向矢量的一个线性组合。由式(17)和式(10)可知，协方差矩阵高阶幂的所有列向量的和向量b是所有信号方向矢量的一个线性组合。即

参照式(4)对a(θi)进行扩展，形成冗余字典D，得到特征向量的稀疏模型为

对式(19)进行稀疏分解得到h,h中非零元素的位置就代表了空间目标的方位信息。不同于l1-SVD方法，本文提出的HOP-SD算法不需要特征值分解，计算量较小。同时不需要估计信号源的数目，增强了算法的鲁棒性。

3.3 稀疏正则化方法

由式(12)或式(19)求得h的过程实际上是一个反问题，反问题的特点亦为其难点就是：它们在Hadamard定义下是不适定的，即在反问题中我们不能完全保证解的存在性、唯一性和稳定性。通常利用正则化方法解决此类问题。尽可能地保证近似解的稳定性的基础上，保留解的尽可能多的信息。由于信号的稀疏特性，使得我们可以找到充分稀疏的唯一解，而且通过这个稀疏扩展就可以精确重构原信号[13,14]。

找到最好的、也就是最稀疏的信号表示，等同于解决下述问题：

其中是序列h中非零项的个数。从一个随机冗余字典中寻找信号的稀疏扩展是一个 NP难问题，为解决这一难点，Chen等人[11]将其转化为解决下述稍有差别的问题：

当上述模型含有噪声时，式(21)的约束条件不再适用，问题转化为最小化目标函数：

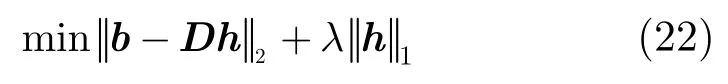
目标函数中前一项反映失配程度，后一项反映稀疏性要求，λ为正则化参数。由于h是复数，它的l1范数为

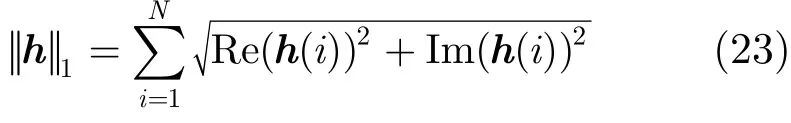
可以发现式(23)的两边平方仍不能消除平方根项，直接导致我们不能使用二次规划的方式最小化目标函数。为了解决这个问题，我们采用二阶锥规划的方法，其转化形式为

利用内点法可以有效解决上述优化问题，得到式(19)中稀疏分解的系数，进而根据非零元素的位置求得信源的DOA估计值。式(22)或式(24)的求解需要参数λ的值，λ的取值不同，所得估值可能不同。故估计式(22)的关键是如何选择合适的参数λ。L-曲线法是较成熟的方法，以对数为横坐标，为纵坐标，并以正则化参数λ为参变量得到类似于“L”形状的拟合曲线图，即。“L”曲线上曲率最大的那点对应的λ值是L-曲线的最优值。图1为式(24)的“L”曲线，根据图1中曲率最大的点可以得到最优的正则化参数λ=0.26。在下文的仿真实验中，正则化参数为0.26。

4 实验及性能分析

实验1 HOP-SD算法中幂指数的选取

HOP-SD算法利用阵列协方差矩阵的高阶幂提取信号子空间作为特征分解的向量，理论上幂指数趋近于无穷大才能收敛到信号子空间，为了分析幂指数m对算法的性能影响，做如下实验：假设来波方向在0～180°内随机产生的2个独立信号入射到5元均匀线阵上，阵元间距为半波长，分别采用不同的幂指数计算 DOA估计的均方根误差随信噪比变化曲线，每个信噪比下进行1000次独立实验(如图2所示)。

从图2可以看出，在较低信噪比(-10 dB)的情况下，较小的幂指数不能使算法收敛到令人满意的程度，均方根误差达到 2.2°。随着幂指数的增大，算法逐渐收敛，幂指数大于等于5时，收敛效果较好，估计的均方根误差小于1°。因此实际应用时，幂指数m取有限整数就能获得很好的收敛性能。下文的仿真实验中，m=5。

实验2 对独立信号的分辨率和估计精度

为了验证算法对两个间隔很近信号的分辨能力，作如下定义：如果对两个信号的估计误差在1°以内，则认为能成功分辨，否则不能分辨。在信噪比15 dB下，2个独立信号入射到5元均匀线阵上，阵元间距为半波长。图3是不同角度间隔下的分辨概率。每个角度间隔下进行1000次独立实验。图4是不同信噪比下的均方根误差，信号的来波方向在0～180°内随机产生，每个信噪比下进行 1000次独立实验。

从图3可以看出，本文提出的HOP-SD和EVSD算法对非相干信号具有较高的分辨率，能分辨出很近的两个信号，分辨性能明显优于MUSIC算法。在低信噪比下EV-SD算法稍优于HOP-SD算法。从图4可以看出，本文提出的方法具有较高的估计精度。在信噪比为-10 dB时，均方根误差小于1°，和l1-SVD方法接近，优于MUSIC算法。

实验3 相干信号的分辨率和估计精度

在信噪比15 dB下，2个相干信号入射到5元均匀线阵上，阵元间距为半波长。图5是不同角度间隔下的分辨概率。每个角度间隔下进行1000次独立实验。图6是不同信噪比下的均方根误差，信号的来波方向在0～180°内随机产生，每个信噪比下进行1000次独立实验。

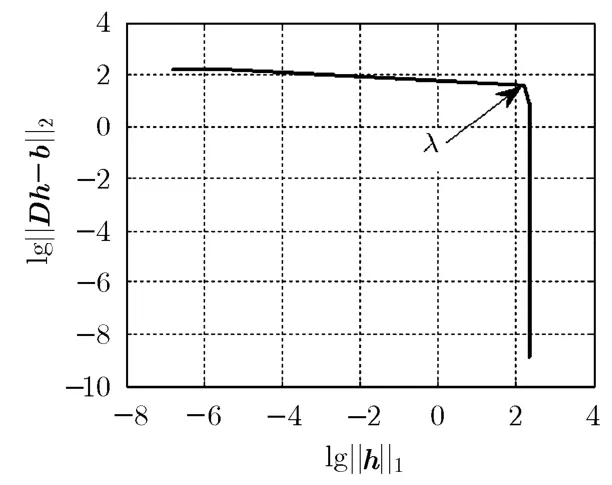
图1 L曲线图

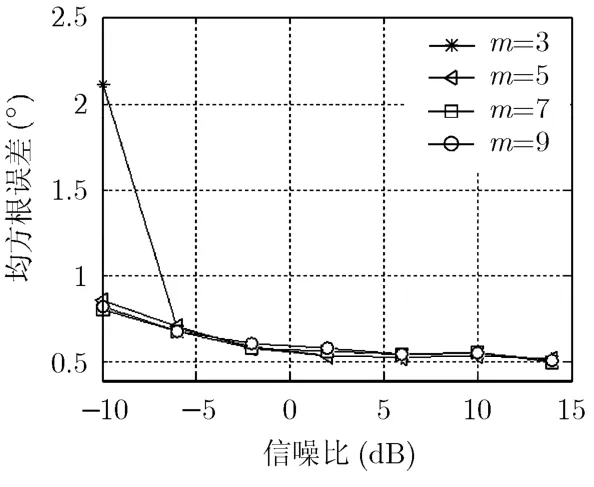
图2 不同幂指数下的均方根误差随信噪比变化曲线

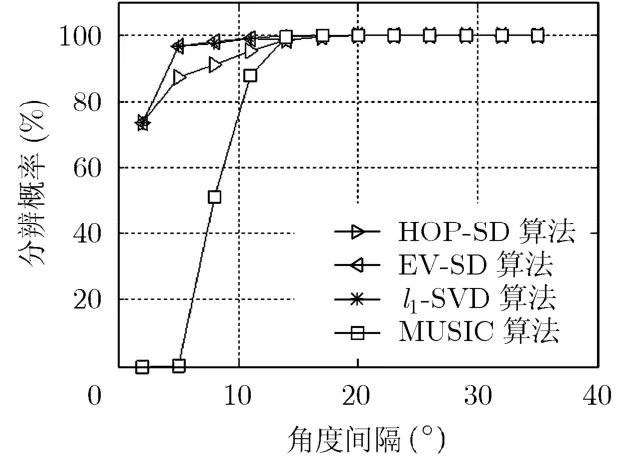
图3 不同角度间隔下的分辨概率(非相干信号)

从图5可以看出，本文提出的 HOP-SD和EV-SD算法对相干信号同样具有较高的分辨率，能分辨出很近的两个信号，在低信噪比下EV-SD算法稍优于HOP-SD算法。而MUSIC算法在相干信号存在的情况下，分辨性能严重下降。从图6可以看出，本文方法对相干信号同样具有较高的估计精度。在信噪比为-10 dB时，均方根误差小于 1°。而MUSIC算法在存在相干信号时，性能严重下降。

图4 不同信噪比下的均方根误差(非相干信号)

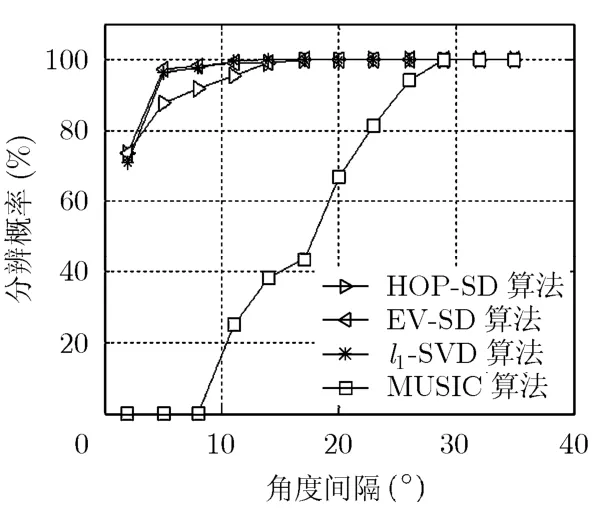
图5 不同角度间隔下的分辨概率(相干信号)

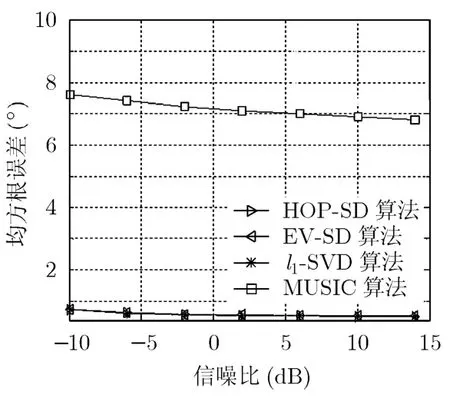
图6 不同信噪比下的均方根误差(相干信号)

实验4 信号源过估计和欠估计时性能

假设来波方向在0～180°内随机产生的2个独立信号入射到5元均匀线阵上，阵元间距为半波长，分别采用l1-SVD算法和本文方法计算DOA估计的均方根误差随信噪比变化曲线，每个信噪比下进行1000次独立实验。图7是信源过估计时的估计精度比较，图8是信源欠估计时的估计精度比较。

从图7可以看出：当信源过估计时，l1-SVD算法的估计精度严重下降，而本文提出的HOP-SD和EV-SD算法不受信源数估计正确与否的影响，不受其影响。从图8可以看出，信源数欠估计时，对l1-SVD算法和本文方法的影响并不大。这主要是因为，信源数欠估计时，l1-SVD算法作为稀疏分解的奇异向量，仍然包含在信号子空间中，并且含有所有信号方向矢量的成分(证明参考式(10))。

5 结论

论文研究了两种基于稀疏分解的 DOA估计方法，理论分析和仿真实验结果验证所提算法具有很高的分辨率和估计精度，同时能够适用于相干信号，不同于l1-SVD方法，本文提出的方法不需要估计信号源的数目，增强了算法的鲁棒性。其中， EV-SD算法的分辨能力和估计精度在低信噪比下稍优于HOP-SD算法。冗余字典的构造和快速高效的稀疏分解算法是稀疏分解在DOA应用中的难点和关键，目前适用于多维 DOA估计的冗余字典的构造正在深入研究之中。

图7 信源过估计时的均方根误差

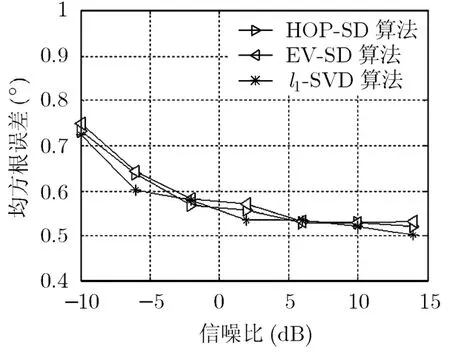
图8 信源欠估计时的均方根误差

[1]Schmidt R O.Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Antennas Propagation,1986,34(3)：276-280.

[2]Samadi S,Cetin M,Masnadi-Shirazi M A,et al..Sparse representation-based synthetic aperture radar imaging[J].IET Radar,Sonar＆Navigation,2011,5(2)：182-193.

[3]Namgook C and Kuo C C J.Sparse MUSIC representation with source-specific dictionaries and its application to signal separation[J].IEEE Transactions on Audio,Speech,and Language Processing,2011,19(2)：326-337.

[4]Dai D and Yang W.Satellite image classification via two-layer sparse coding with biased image representation[J].IEEE Geoscience and Remote Sensing Letters,2011,8(1)：173-176.

[5]Namgook C and Kuo C C J.Sparse representation of musical signals using source-specific dictionaries[J].IEEE Signal Processing Letters,2010,17(11)：913-916.

[6]Gao Xiang-yun and Zhang Tian-qi.Multi parameter estimation of wideband chirp signals based on OMP decomposition[C].IEEE International Conference on Information Theory and Information Security,Beijing,Dec.17-19,2010：722-727.

[7]Md Mashud Hyder and Kaushik Mahata.Direction-of-Arrival estimation using a mixedl2,0norm approximation[J].IEEE Transactions on Signal Processing,2010,58(9)：4646-4655.

[8]Guo Xian-sheng,Wan Qun,Chang Chun-qi,et al..Source localization using a sparse representation framework to achieve superresolution[J].Mulitidimensional Systems and Signal Processing,2010,21(4)：391-402.

[9]Zhang Shu,Li Yu-mei,and Song Jun-cai.A novel method for DOA estimation based on generalized-prior distribution[C].2010 International Conference on Measuring Technology and Mechatronics Automation,Changsha,China,2010：244-247.

[10]Malioutov D,Cetin M,and Willsky A S.A sparse signal reconstruction perspective for source localization with sensor arrays[J].IEEE Transactions on Signal Processing,2005,53(8)：3010-3022.

[11]Chen Hao-bing,Donoho D L,and Saunders M A.Atomic decomposition by basis pursuit[J].SIAM Joumal on ScientificCompting,2001,20(1)：33-66.

[12]Cadzow J A,Kim Y S,and Shiue D C.General direction-ofarrival estimation：a signal subspace approach.IEEE Transactions on Aerospace and Electronic Systems,1989,25(1)：31-46.

[13]Donoho D and Huo X.Uncertainty principles and ideal atomic decompositions[J].IEEE Transactions on Information Theory,2001,47(7)：2845-2862.

[14]Elad M and Bruckstein A M.A generalized uncertainty principle and sparse representation in pairs of bases[J].IEEE Transactions on Information Theory,2002,48(9)：2558-2567.