一种复合多基地雷达密集多目标检测的新方法
闵 涛 赵 锋 肖顺平
(国防科技大学电子科学与工程学院 长沙 410073)
1 引言
在利用常规探测手段的情况下,当多个目标位于雷达天线波束范围内,且各目标的回波信号在时域或频域难以分辨时,称这些目标为不可分辨多目标或密集多目标。在防空反导背景下,如果雷达对密集多目标情况缺乏特殊处理能力,而只是一味地当作单目标而以传统方法来处理的话,将会带来一系列的严重后果。当前的单基地雷达往往具有好的距离分辨率,但角度分辨率比较差,从而导致不可分辨的目标测量,这可能引起目标检测和跟踪中的严重错误。在已发表的文献中[1-4],相关研究人员对于解决这个问题作了一些尝试,取得了不少研究成果,但大多还只是限于理论研究阶段,而且由于实际应用环境的复杂性,理论上仍存在许多不完善之处。
双/多基地雷达是最早出现的雷达体制,除了反隐身、抗干扰等传统优势[5],其在目标信息获取、工作方式、技术实现等方面体现出的多样性,使得利用双/多基地雷达对密集多目标进行探测具备一定的可行性。文献[6]利用多基地雷达消除多路径假目标的影响。Bradaric等人[7]以多基地雷达模糊函数为工具对多基地雷达系统进行分析和设计,通过波形选择、传感器部署、接收机信号加权这3种方式及其联合使用来改善雷达系统的分辨能力。文献[8,9]同样以多基地雷达模糊函数为工具,分析了空间相关和非相关多基地雷达系统的分辨性能。以上是利用双/多基地雷达改善目标定位和分辨的一些例子,但涉及密集多目标探测的研究比较少,特别是信号处理方面的研究。
Nandakumaran等人[10]考虑一个在信号层次融合的复合双基地雷达系统对密集多目标进行探测,但没有分析检测门限、目标起伏及复合双基地雷达几何配置对密集多目标检测的影响,同时只考虑了2维平面,仅解决了 1维角度上的不可分辨问题。本文在此基础上,针对 3维空间,利用 T/R-R2复合多基地雷达对密集多目标进行检测,分析了可能影响检测的各个因素,并重点研究了复合多基地雷达在不同检测门限、目标起伏和几何配置下的多目标检测性能。
2 复合多基地雷达目标回波信号模型
复合双/多基地雷达是在单基地雷达(T/R站)的基础上,增加一个或多个相隔一定距离的接收机(R站)。本文考虑一个T/R-R2复合多基地雷达系统,其几何配置如图1所示,T/R站分别与R1站和R2站构成 T/R-R复合双基地雷达系统。T/R站发射的信号经目标散射后分别被T/R站、R1站和R2站接收,3部接收机可以通过单基地雷达和多基地接收机1,接收机2间直接链路上的信号进行同步。
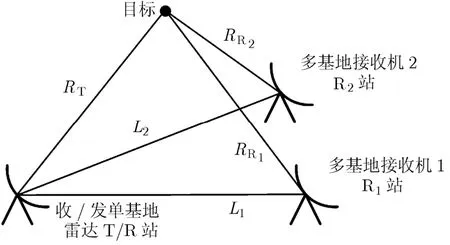
图1 T/R-R2复合多基地雷达的几何配置
在2维平面上,考虑T/R-R复合双基地雷达,单基地雷达具有圆形距离等值线,其距离单元宽度由脉冲宽度确定;而双基地雷达的距离和等值线为椭圆形,其距离单元宽度随目标在距离和等值线上的不同位置而改变,但变化范围不大。这样发射机关注区域被单基地接收机的圆形距离等值线和双基地接收机的椭圆形距离和等值线划分为平面上的栅格,如图2中实线所示,N,N1,N2分别为3部接收机的距离单元数。常规雷达距离分辨率比较高,假设这些栅格足够分辨目标(即假设每个栅格最多存在一个目标,反之亦然)。考虑3维空间,如图2所示,距离(和)等值线转化为等值面。单基地接收机、多基地接收机1,接收机2距离单元数分别为2,2,1(垂直于纸面方向),4个目标分别位于3部接收机距离单元划分的空间栅格中。在图2的基础上,图3中多基地接收机 2垂直于纸面方向向外增加了一个距离单元,8个目标分别位于3部接收机距离单元划分的8个空间栅格中。同样假设这些空间栅格足够分辨目标。则同一平面的多个目标,通过平面栅格区分开来;不同平面的目标,通过空间栅格区分开,这样就实现了3维空间的多目标分辨。
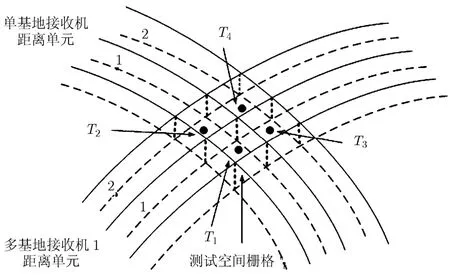
图2 4目标存在情况下的复合多基地雷达的空间栅格(N=2,N1=2,N2=1)
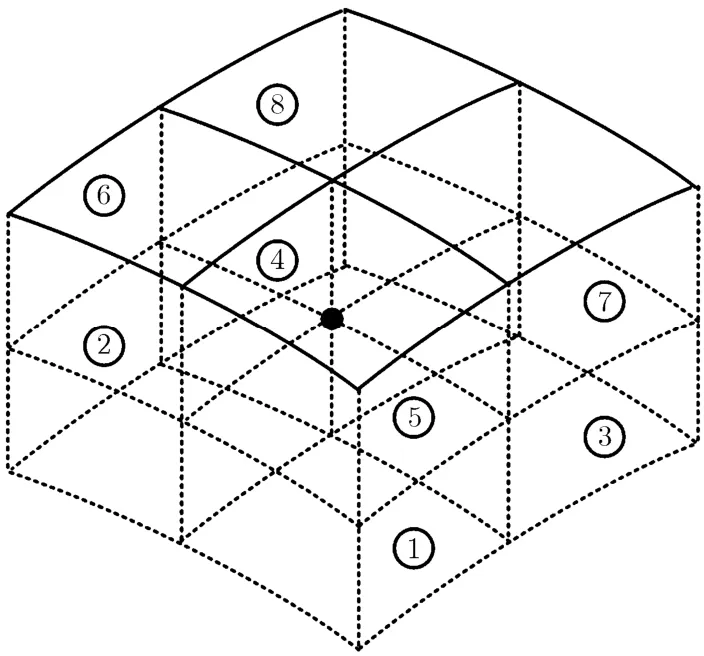
图3 8目标存在情况下的复合多基地雷达的空间栅格(N=2,N1=2,N2=2)
假设3部雷达接收机参数相同,目标相对于多基地接收机1,接收机2的双基地RCS也一致。单基地接收机和多基地接收机 1,接收机 2所接收的信号功率可表示为[10]
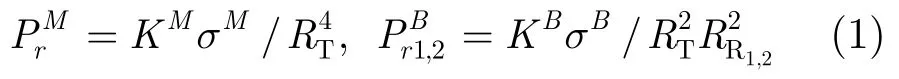
其中σM,σB为目标的单基地、双基地目标RCS,RT为单基地接收机到目标的距离,,RR2分别为多基地接收机1,接收机2到目标的距离,KM为单基地接收机的雷达常数,包含发射机峰值功率、天线增益、雷达波长、综合损耗等因素,KB为多基地接收机的雷达常数。从式(1)可看出,与单基地雷达距离等值线为圆形不同,双基地距离和等值线为椭圆形;双基地距离和等值线不与信噪比等值线共线,因此回波功率随目标在距离和等值线上的不同位置而变化。这些几何特性为解决不可分辨目标的问题提供了额外的信息。对应于单基地接收机一个距离单元的匹配滤波输出可表示为[10]
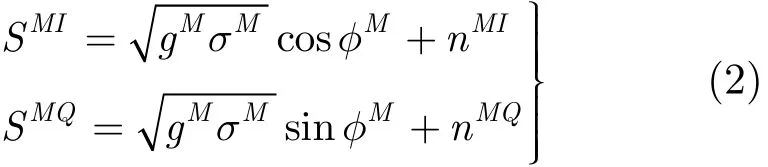
其中SMI和SMQ为同相和正交两个通道的分量,由信号和噪声叠加的形式表示,为单基地相位角。不失一般性,噪声nMI,nMQ可认为服从零均值高斯分布,方差为。类似地对应于多基地接收机 1,接收机 2一个距离单元的匹配滤波输出同相和正交通道的输出分量可表示为
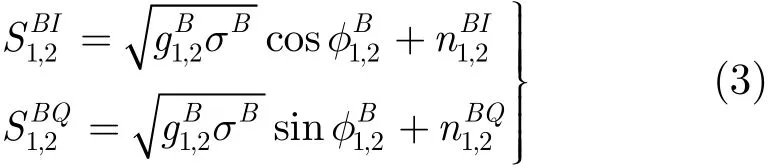
假设目标RCS起伏模型为Swerling II型(后面的仿真实验将证明,此假设条件下的推导结果对其它起伏类型的目标仍然适用),目标由几个相等强度的散射点组成,散射点都具有均匀分布的相位角φM,则脉冲间目标散射面积电压值服从瑞利分布,即服从瑞利分布,相位因子可视为在[0,2π]内均匀分布,则服从零均值高斯分布,即方程式(2)中两式的第 1项均服从零均值高斯分布,由于噪声也服从零均值高斯分布,因此同相和正交信号均服从零均值高斯分布,即
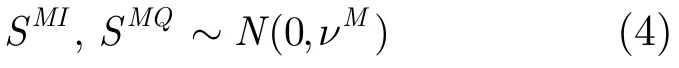

其中P为散射点的数量,σp为第P个散射点的RCS,φp为第P个散射点相对于第1个散射点的散射场相位。由于Swerling II型目标的散射点具有均匀分布的相位角,通过将确定的相位角φp合成为φB可将单基地接收机的信号分布形式扩展到多基地接收机的情况,即
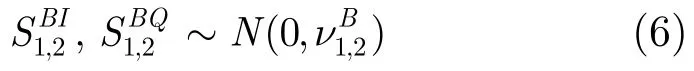
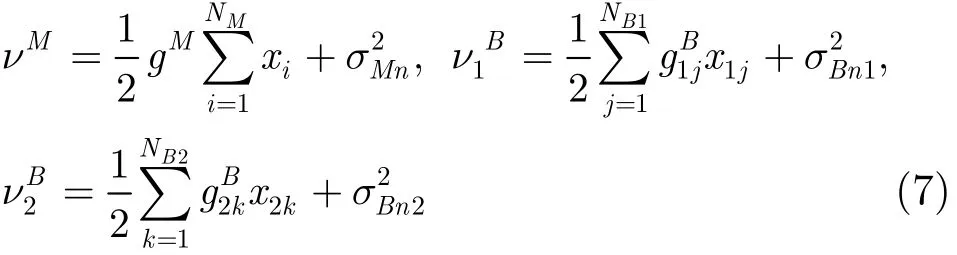
其中NM和NB1,NB2分别表示给定单基地接收机距离单元、多基地接收机 1,接收机 2距离单元中多目标的个数。单基地功率增益因子gM对于给定的单基地距离单元为常数,而双基地功率增益因子沿给定双基地距离单元会发生变化,RTj,RTk为目标到发射机的距离,RR1j,RR2k为目标到多基地接收机1,接收机2的距离。
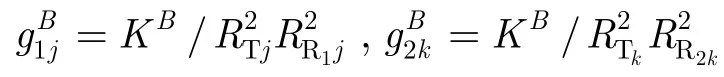
3 复合多基地雷达信号融合
在密集多目标情况下,复合多基地雷达目标回波包含来自单基地接收机的同相信号和正交信号,以及来自多基地接收机 1,接收机 2的同相信号和正交信号。F为雷达发射子脉冲的个数,M,B1,B2分别为可能包含目标的单基地接收机距离单元、多基地接收机1距离单元、多基地接收机2距离单元的数目。根据第2节的讨论,以上信号的分布形式可表达为
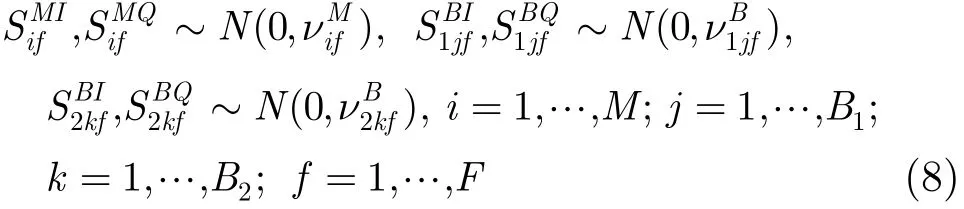
根据式(7),考虑到3部接收机距离单元相交形成空间栅格,式(8)中的方差可表达为
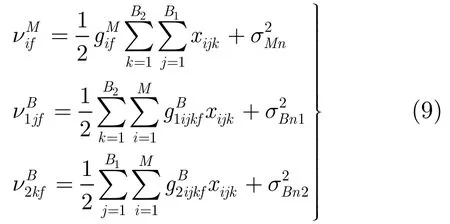
其中为栅格(i,j,k)中目标的平均 RCS,和,分别为单基地和多基地接收机1,接收机2的功率增益因子。给定单基地接收机和多基地接收机 1,接收机 2距离单元的概率密度函数可表示为
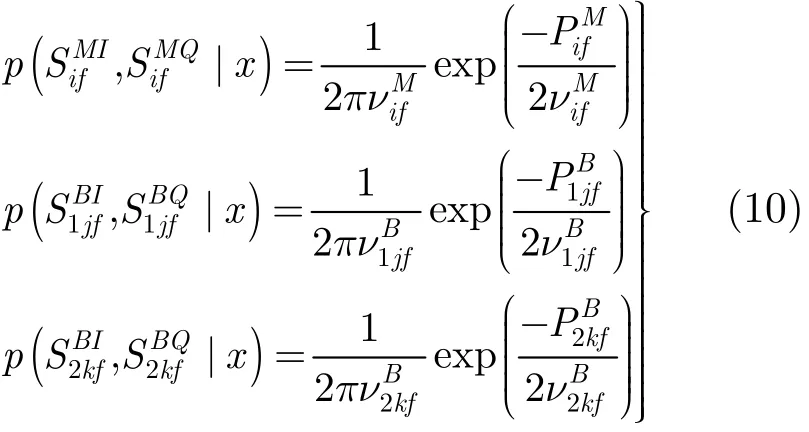
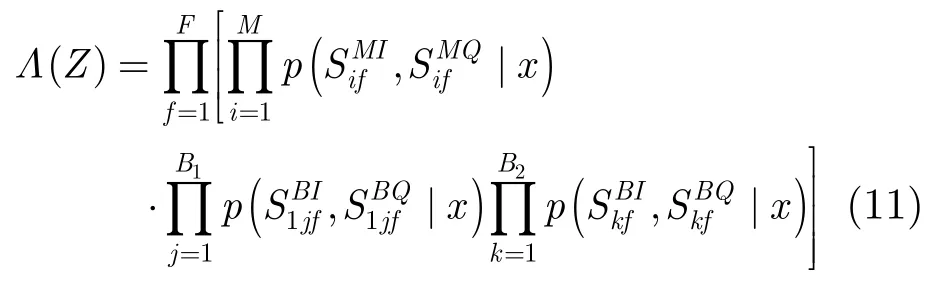
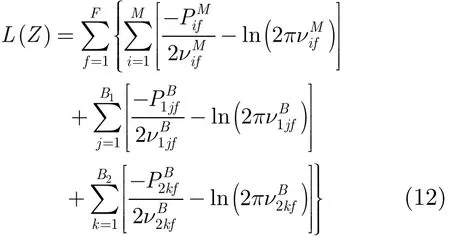
对于某栅格(I,J,K),为了判断其中是否存在目标,将式(12)对xIJK求导并令导数为零,使L(Z)取得极值(最大值),从而得到xIJK估计值。由于xIJK与脉冲积累数、目标个数等诸因素有关,根据导数方程难以求得其解析表达式,只能通过数值仿真求L(Z)的最大值得到最优xIJK值,即
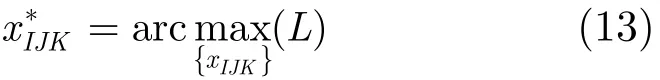
将最优值与门限相比较,得出栅格(I,J,K)中是否存在目标,从而得到多目标的检测结果。假设H0代表栅格(I,J,K)内不存在目标,H1代表栅格(I,J,K)内存在目标。根据检测统计量及检测门限η,判决准则δ可表示如下:
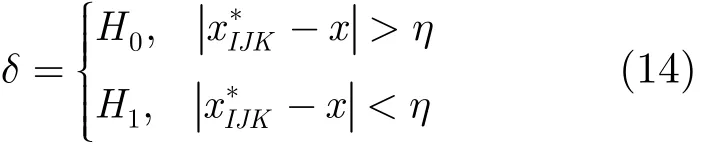
4 仿真结果及性能分析
仿真中假设复合多基地雷达所检测的多个目标的位置如图3所示。多目标所在区域距离单基地接收机、多基地接收机1,接收机2的距离分别为80 km,50 km,50 km。假设各接收机距离单元的宽度均为25 m(忽略多基地接收机距离单元宽度随目标在距离和等值线上的不同位置而变化)。雷达发射机峰值功率为350 kW,中心频率为4 GHz,发射天线增益、各接收机天线增益均为 40 dB,发射子脉冲个数为10。目标起伏默认均为Swerling II型,均具有2 m2的平均RCS。蒙特卡洛仿真次数为10000。
以(X,Y,Z)表示目标所在的空间栅格,X,Y,Z分别表示目标所在单基地接收机、多基地接收机 1,接收机 2的距离单元序号。结合图2,图3,目标T1位于测试空间栅格(1,1,1),目标T2,T3,T4,T5,T6,T7,T8分别位于相邻空间栅格(1,2,1),(2,1,1),(2,2,1),(1,1,2),(1,2,2),(2,1,2),(2,2,2)。单目标情况下,T1位于测试栅格(1,1,1),假设H0和H1分别表示测试栅格内不存在目标或存在目标的情况。多目标情况下,T1位于测试栅格(1,1,1),其它目标位于邻近空间栅格,假设H0和H1分别表示当邻近栅格一直存在目标时,测试栅格内不存在目标或存在目标的情况。仿真目的是分析不同条件下各接收机同一距离单元内的角度不可分辨目标和不同距离单元内的目标对目标T1检测的影响。
4.1 最优平均RCS概率密度仿真结果
首先,不考虑与门限比较后的检测结果,只考虑使L(Z)取得最大值的最优平均RCS的分布情况。图4给出了不同目标个数、不同信噪比情况下最优平均RCS的概率分布曲线。
根据检测准则,最优平均RCS的分布越是集中于2 m2附近,目标的检测效果越好。从图4可以看出,平均RCS的分布情况随着信噪比的增大而更有利于对目标T1的检测。随着目标数量的增加,同一距离单元内的角度不可分辨目标对测试栅格中的目标检测会有干扰。比较图4(a)-4(f)可以看出,增加一个目标后,目标T1的平均RCS分布情况明显变差,但影响程度不一:T2,T5与T1位于单基地接收机同一距离单元内,同时T5与T1位于多基地接收机1同一距离单元内,T2与T1位于多基地接收机2同一距离单元内,T2,T5的影响均较大;而T4与T1仅位于多基地接收机 2同一距离单元内,T6与T1仅位于单基地接收机同一距离单元内,相对T2,T5影响较小;T8与T1不在单基地接收机或多基地接收机1,接收机2同一距离单元内,所以T8对T1的检测影响非常小,图4(a),4(f)中最优平均 RCS的分布情况基本相同。从图4(g),4(h),4(i)中可以看出,目标数量增加,检测性能将进一步变差;图4(i)中8目标同时存在,目标T1的平均RCS分布情况最差,特别是在较低信噪比情况下比较明显。
4.2 检测概率仿真结果
图5,图6分别给出了不同目标个数、不同信噪比情况下检测概率与检测门限、目标到多基地接收机1,接收机2距离间的关系曲线。从图5(a)-5(c)可以看出,检测概率随着信噪比的增大而增大,与图4中最优平均RCS的概率分布情况相吻合。同时检测概率随着检测门限的增大而增大。图5(d),5(e)表明,在高信噪比情况下,目标数量增多,检测概率变小。从图5(f)可以看出,低信噪比情况下,目标数量增多,当检测门限较大时,检测概率依然变小;但当检测门限较小时,检测概率反而变大。
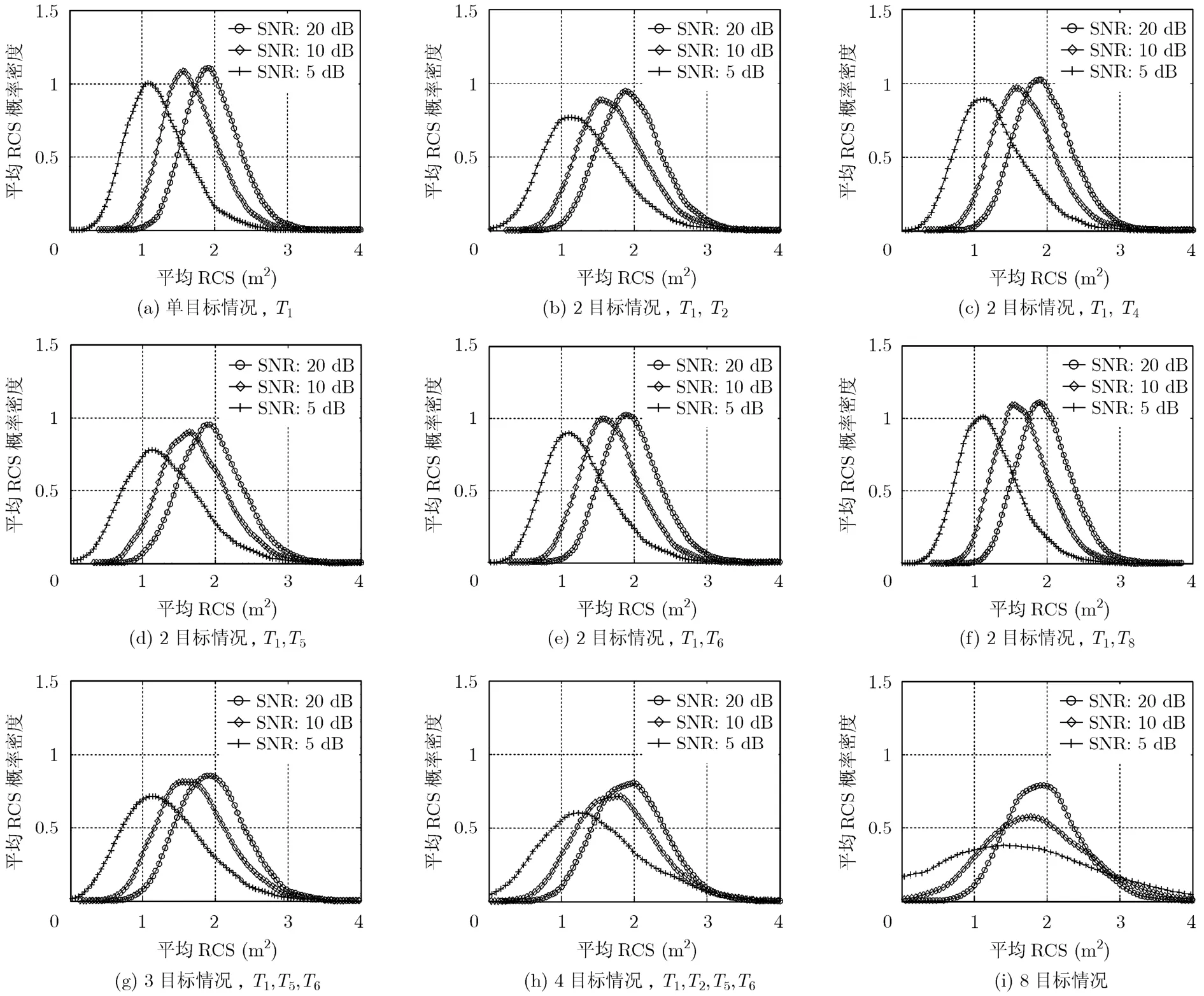
图4 最优平均RCS的概率分布(RT=80 km,RR1=50 km,RR2=50 km)

图5 检测概率与检测门限关系曲线(RT=80 km,RR1=50 km,RR2=50 km)
从图6(a),6(b)可以看出,目标到单基地接收机、多基地接收机2距离RT,RR2不变情况下,目标到多基地接收机1距离RR1在20-100 km之间变化时,对检测概率影响比较小。从图6(c)可以看出,RT,RR1不变,RR2改变或RR1,RR2不变,RT改变带来的影响也是相似的。由于模型只利用了复合多基地雷达的距离信息,在雷达径向距离分辨率足够高的情况下,只要复合多基地雷达的几何配置能够保证3个接收机的距离单元相交后形成的空间栅格足够分辨目标,其它的几何配置因素就不会对密集多目标的检测产生大的影响。同时,我们还可以从图6中再次印证图4,图5中的结论:在各种目标数量情况下,检测概率随着信噪比的增大而增大;比起单目标检测情况,目标数量的增加会导致检测效果变差,这在高信噪比的情况下可以体现出来,而在低信噪比情况下却相反,这是由于选择的门限值为0.5,比较低,结合图5(f)也可得出相同结论。因此,结合图5,图6得出结论,在目标数量、信噪比、检测门限选择方面要有一个综合的考虑,以取得最好的检测效果。

图6 检测概率与目标到多基地接收机距离关系曲线(η=0 .5,RT =80 km)
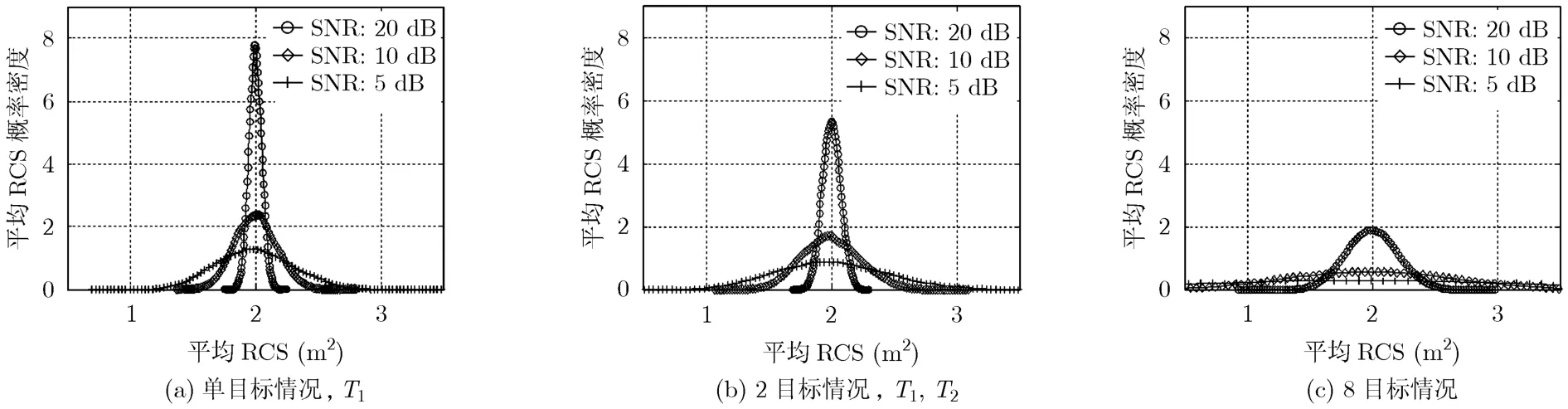
图7 Swerling 0型目标最优平均RCS的概率分布(RT=80 km,RR1=50 km,RR2=50 km)
4.3 其它目标起伏类型条件下仿真结果
(1)最优平均RCS概率密度仿真结果 图7,图8分别给出了Swerling 0,IV型目标起伏条件下最优平均RCS的概率分布曲线。可以发现,对于Swerling 0和IV型目标来说,信噪比及其它目标对所检测目标最优平均RCS概率分布的影响与Swerling II型目标相似:平均RCS的分布情况随着信噪比的增大而更有利于对目标T1的检测。随着目标数量的增加,同一距离单元内的角度不可分辨目标对测试栅格中的目标检测会有干扰。
(2)检测概率仿真结果 图9,图10给出了3种目标起伏条件下的检测概率仿真结果,目标数量分别为1,2,8,其它多目标假定情况下有相似的结果。SNR为信噪比,η为检测门限值。图9中,不同数量目标情况下,3种目标起伏条件下的检测概率随着信噪比的增大而增大,Swerling II型起伏条件下检测概率最小,Swerling 0型起伏条件下检测概率最大。图10中,3种目标起伏条件下,RT,RR2不变时,RR1在20-100 km之间变化时,对检测概率的影响比较小,Swerling II型起伏条件下检测概率最小,Swerling 0型起伏条件下检测概率最大。随着目标数量的增多,3种目标起伏条件下的检测概率均有所下降。
图7-图10中的仿真结果表明,虽然Swerling II型目标为本文推导的假设条件,其它两种目标起伏类型虽然不符合本文算法的假设条件,但这两种情况下检测算法仍然有效。
图4-图10中不同条件下密集多目标检测的仿真结果对比表明,目标到3部接收机的距离变化以及各接收机不同距离单元中的目标干扰对检测的影响比较小,信噪比、目标数量、目标起伏、各接收机同一距离单元内的角度不可分辨目标的干扰以及检测门限是影响检测性能的主要因素。
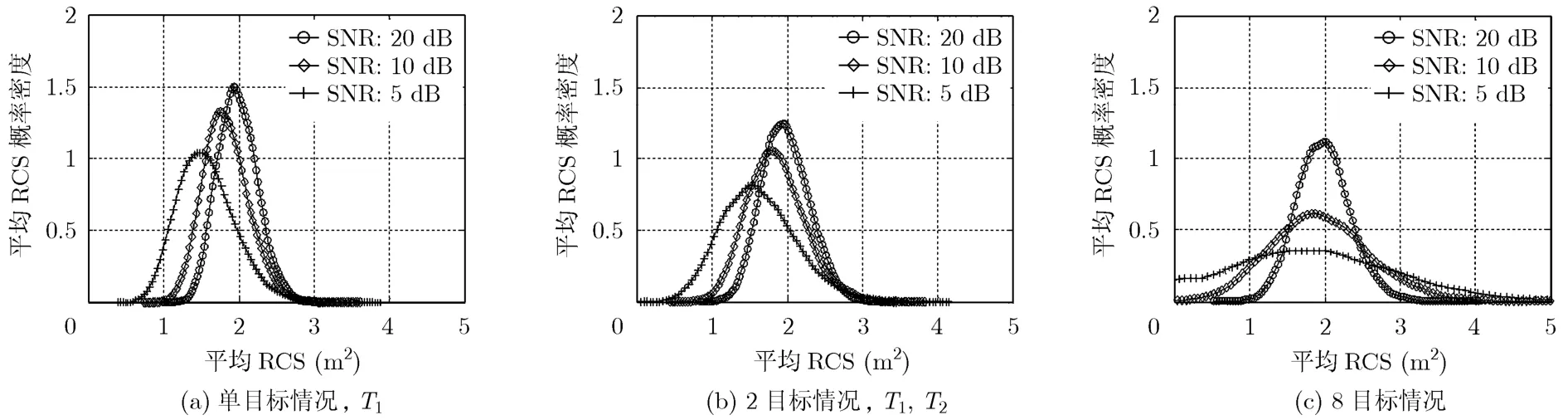
图8 Swerling IV型目标最优平均RCS的概率分布(RT=80 km,RR1=50 km,RR2=50 km)
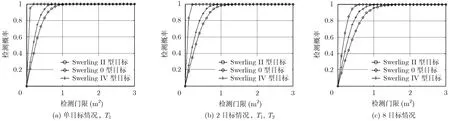
图9 不同目标起伏条件下检测概率与检测门限关系曲线(SNR=20 dB,RT=80 km,RR1=50 km,RR2=50 km)

图10 不同目标起伏条件下检测概率与目标到多基地接收机1距离关系曲线(η=0 .5,SNR=20 dB,RT =80 km,RR2=50 km)
5 结束语
提高雷达对密集多目标的探测能力是当前雷达技术领域所面临的前沿课题和紧迫任务,本文通过T/R-R2复合多基地雷达系统的信号融合,利用距离信息对不同数量的密集多目标进行了检测,并分析了信噪比、目标数量、目标起伏、检测门限和复合多基地雷达几何配置等因素对检测性能的影响。本文的研究成果,不仅能用于对双/多基地雷达密集多目标检测性能的分析,还能为双/多基地雷达布站提供一定的理论参考。本文融合的信息为径向距离,可利用的信息还包含切向距离、角度、径向速度等。对于包含在单个接收机同一距离单元内的多个目标,研究通过去相关信号处理算法,消除同一距离单元内其它目标的干扰,改善密集多目标探测性能,是可以进一步拓展的工作。
[1]Peebles P Z and Berkowitz R S.Multiple-target monopulse radar processing techniques[J].IEEE Transactions on Aerospace and Electronic Systems,1968,4(6):845-854.
[2]Sinha A,Kirubarajan T,and Bar-Shalom Y.Maximum likelihood angle extractor for two closely spaced targets[J].IEEE Transactions on Aerospace and Electronic Systems,2002,38(1):183-203.
[3]Zhang Xin,Willett P K,and Bar-Shalom Y.Monopulse radar detection and localization of multiple unresolved targets via joint bin processing[J].IEEE Transactions on Signal Processing,2005,53(4):1225-1236.
[4]Nandakumaran N,Sinha A,and Kirubarajan T.Joint detection and tracking of unresolved targets with monopulse radar[J].IEEE Transactions on Aerospace and Electronic Systems,2008,44(4):1326-1341.
[5]杨振起,张永顺,骆永军.双(多)基地雷达系统[M].北京:国防工业出版社,1996:19-22,254.Yang Zhen-qi,Zhang Yong-shun,and Luo Yong-jun.Bistatic(Multistatic)Radar Systems[M].Beijing:Publishing House of National Defence Industry,1996:19-22,254.
[6]Seliga T A and Coyne F J.Multistatic radar as a means of dealing with the detection of multipath false targets by airport surface detection equipment radars[C].2003 IEEE Radar Conference,Huntsville,Alabama,USA,2003:329-336.
[7]Bradaric I,Capraro G T,Brady S H,et al..Multistatic measurements in a controlled laboratory environment[C].2010 IEEE Radar Conference,Washington DC,USA,2010:266-270.
[8]Derham T.Doughty S,Baker C,et al..Ambiguity functions for spatially coherent and incoherent multistatic radar[J].IEEE Transactions on Aerospace and Electronic Systems,2010,46(1):230-245.
[9]Adjrad M and Woodbridge K.A framework for the analysis of spatially coherent and incoherent multistatic radar systems[C].2011 7th International Workshop on Systems,Signal Processing and Their Applications,Tipaza,Algeria,2011:155-158.
[10]Nandakumaran N,Sinha A,and Kirubarajan T.Hybrid radar signal fusion for unresolved target detection[C].Signal and Data Processing of Small Targets 2007,San Diego,California,USA,2007,Proceedings of SPIE Vol.6699,669911,1-8.

