两种不同抽样方式下样本均值的数学期望和方差的比较

刘淑华

(长春理工大学 光电信息学院，长春 130021)

两种不同抽样方式下样本均值的数学期望和方差的比较

刘淑华

(长春理工大学 光电信息学院，长春 130021)

给出了在有放回抽样时，样本均值的数学期望和方差的计算结果;同时通过引理的证明给出了在无放回抽样方式下，样本均值的数学期望和方差的结果。从而说明了在抽样方式不同的情况下，样本均值的数学期望相同，但方差却是不同的，但是，当样本容量n很大时，则两者的差别是不大的;当n趋于无穷大时，这两者就没有区别了。

总体;样本;样本均值;样本方差

在数理统计中，我们经常要用到从总体中抽取的样本构成的统计量的分布。当总体服从正态分布时，样本均值和样本方差的分布都是确定的，由样本均值和样本方差构成的某些统计量服从的分布也比较容易计算。一般情况下，统计量的分布不是很容易计算，但统计量的数字特征相对来说计算还是比较容易的，同时这些统计量的数字特征的计算又是非常必要的。特别是样本均值的数学期望和方差的计算。一般来说，从总体中抽样的方式不同，会影响到样本均值的数学期望和方差，为了在一种特殊的抽样方式之下也能求出样本均值的数学期望和方差，我们先来证明一个引理。

1 引理

口袋中有N张卡片，上面分别写有数字Y1，Y2，…，YN，不放回的从中抽出n张，则其和的数学期望和方差分别为

以ηn表示n张卡片上的数字之和，以Xi，i=1，2，…，n表示第i次抽到的卡片上的数字，则ηn=X1+X2+…+Xn

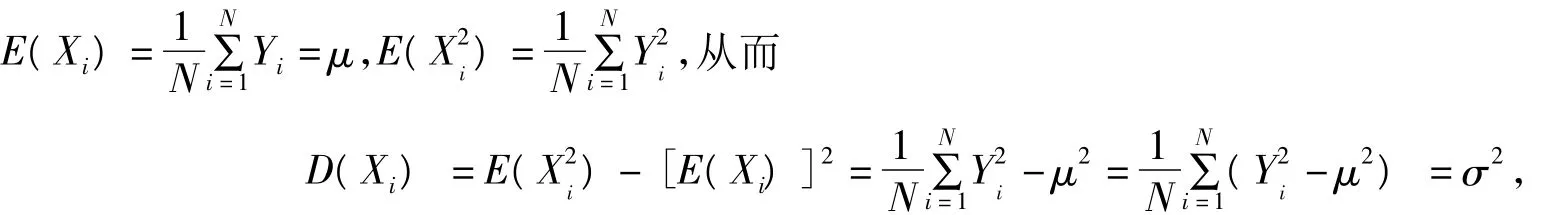
所以ηn的数学期望为

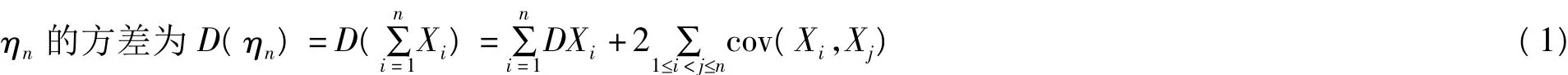
由协方差的对称性和Xi之间的对称性可知

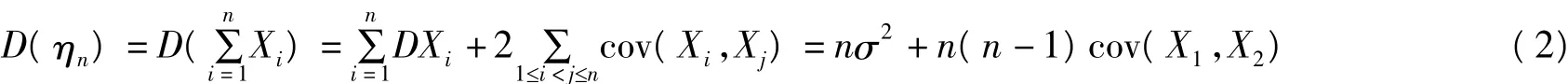
在(2)式中，令n=N，这时ηN=X1+X2+…+XN是一个常数，从而D(ηN)=0，代入到(2)中，可得

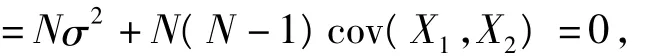
将上述结果代入到(2)式中，可得

2 样本的抽取方式为有放回的情况

样本的抽取方式为有放回的情况下，获得的样本为简单随机样本，即从总体中抽出的样本为相互独立并且与总体同分布。不妨设总体的数学期望和方差都存在，并且E(X)=μ，D(X)=σ2。从总体中抽出容量为n的样本为样本均值，由于X1，X2，…，Xn相互独立，并且与总体同分布，从而，样本均值的数学期望和方差分别为

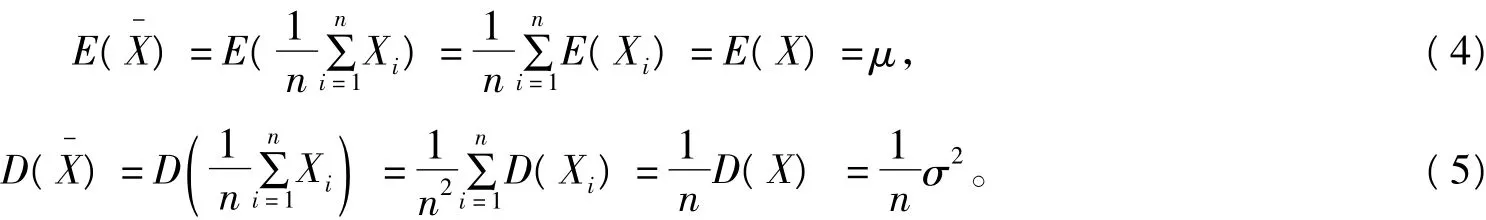
3 样本的抽取方式为无放回的情况

当抽样方式为无放回的情况时，下一次抽样是受前一次抽样的结果的影响的。此时，设总体中包含N个个体，从总体中抽取容量为n的样本X1，X2，…，Xn，

则此时X1，X2，…，Xn，不满足相互独立性，但与总体同分布，所以仍然有E(Xi)=μ，D(Xi)=σ2，从而

将上述结果代入(7)式，则有

即有

4 结论

通过将(5)与(7)的比较，我们看到，当抽样方式为无放回的时候，样本均值的期望不变，但方差发生了变化，与有放回抽样相比，多了一个倍数当n与N相差不大时，(5)与(7)的差别是很大的;当N远远大于n时，(5)与(7)的结果基本相近;当N趋于无穷大时，(5)与(7)的结果就没区别了。

［1］ 李贤平.概率论基础［M］.北京：高等教育出版社，1987.

［2］ 同济大学应用数学系.工程数学概率统计简明教程［M］.北京：高等教育出版社，2003.

责任编辑：程艳艳

Comparison of Mathematical Expectation and Variance of Sample Mean by Means of Two Different Sampling Methods

LIU Shu-hua
(College of Optical and Electronical Information，Changchun University of Science and Technology，Changchun 130022，China)

This paper gives the calculation results of mathematical expectation and variance of sample mean in sampling scheme with replacement，at the same time，it presents the results of mathematical expectation and variance of sample mean in sampling scheme without replacement by using lemmas.So we can prove that the mathematical expectation of sample mean is same while the variance is different in different patterns of sampling.But when the sample size n is very large，the difference is slim and when the sample size n tends to infinite，the difference is little.

overall;sample;sample mean;sample variance

O212.2

A

1009-3907(2012)08-0983-03

2012-06-18

刘淑华(1971-)，女，内蒙古哲里术盟人，讲师，硕士，主要从事概率论与数据统计方面的研究，