微波在片测试数据离散剔除算法研究
曹敏华,康耀辉,顾 梅,陈金远,张新焕
(中国电子科技集团公司第55研究所,南京 210016)
1 引言
微波在片测试是利用探针在微波探针台上对MMIC圆片进行微波性能测试的一种方法,它能够在流水线上评价MMIC的性能,还能快速准确地提供有意义的统计数据。另外,微波在片测试不对芯片进行任何金丝键合及烧结等装架,减少了装架和封装的成本,并排除对微波性能的附加影响[1]。它在不影响芯片的情况下测试芯片性能、剔除不合格品,为保证交付合格裸片给用户提供了有效检测手段。微波在片测试有在片测试项目多、参数种类复杂、频点密集及数据量庞大等特点。微波在片测试数据处理的灵活性很大,以前基本靠人工手动处理。随着虚拟仪器与传统自动化测试系统联合测试设备的应用[2],微波在片测试圆片级自动测试速度得到了极大提升,出片量有了很大增加。同时,新的测试项目和参数又不断出现,测试数据越来越多,单靠手动处理数据已远远不够,必须寻求高效率的软件自动数据处理方法。
2 工艺控制微波数据处理软件现状
目前,可以在片测试的典型微波芯片种类和主要测试参数包括:(1)功率放大器芯片,主要微波参数为小信号线性增益、大信号功率增益、1dB功率压缩点(P-1)、功率平坦度、大/小信号增益的幅度/相位一致性、大信号动态电流及效率;(2)低噪声放大器芯片,主要微波参数为小信号增益、1dB功率压缩点(P-1)及噪声系数;(3)控制类芯片,主要微波参数为插入损耗,移相态/衰减态、隔离度、幅度均衡、移相(衰减)精度、基态幅度/相位一致性;(4)混频器芯片,主要微波参数为变频损耗、噪声系数、1dB功率压缩点(P-1);(5)多功能芯片,主要微波参数为各个组成芯片参数的集合。通常不同芯片需要测试的参数不同,数据处理要求和方法也不同,为此,我们开发了工艺控制微波数据处理软件,它能够根据不同圆片版图和测试规范,自动进行合格数据筛选处理工作;但是经过该软件处理过的合格数据中总会有一些离散大的芯片数据,如个别数据明显偏离大部分数据形成的曲线包络,或个别数据的斜率与主包络数据的斜率明显不同甚至相反(图1)。
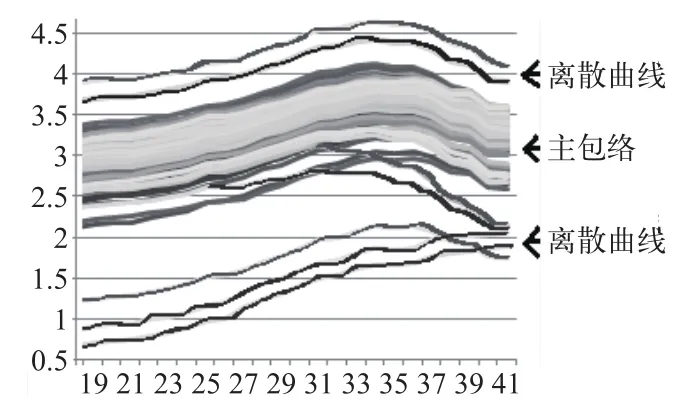
图1 离散曲线图
离散数据对应的芯片可能位于圆片边缘,也有些芯片虽然不在边缘,但其性能偏大或偏小于大多数芯片,从整个圆片的性能一致性、稳定性和可靠性等方面考虑,有必要剔除掉离散数据对应的芯片。但由于这些离散数据本身满足测试规范,也没有定性指标或计算公式可循,故不能被处理微波数据的工艺控制软件筛选出来。如何将大批测试数据中的这些少量离散大的数据剔除掉是一个比较棘手的问题。
3 离散剔除算法
传统的剔除离散数据的方法是用EXCEL表格画图来查看数据的离散情况,根据图示结果剔除掉离散曲线。EXCEL表格画图的优点是比较直观、一目了然;但该方法需要人工手动画图并人为判断是否可以剔除掉,如果芯片个数很多,数据行数超过255行(EXCEL最多只能对255行数据进行画图),则需分批画图查看,处理数据的效率很低。为了完善工艺控制微波数据处理软件,实现自动剔除离散数据的功能,作者尝试了多种离散剔除算法并应用于数据处理软件中。
3.1 模拟EXCEL表格画图法
将某一个参数项中每一个频点的数据按照从小到大的顺序进行排序,计算每一列数据的均值和相邻数据的差值,然后计算相邻数据的差值占整个数据的比值百分比,设定比值百分比的上限。如果大于均值的某相邻差值百分比超出设定上限,则删除相邻数据中较大的数据及该数据以上的数据;如果小于均值的某相邻差值百分比超出设定上限,则删除相邻数据中较小的数据及该数据以下的数据,如图2所示。

图2 模拟EXCEL表格画图法示例
假设在f1频点,Δ1超过了拟定的比值百分比上限,因为曲线b的数值大于该频点的测试数值的均值,并且曲线b是产生Δ1的相邻2个曲线中数值较大的曲线,则曲线b及曲线b以上的曲线a一起会被剔除掉;同理,Δ2超过了拟定的比值百分比上限,因为曲线c的数值小于该频点的测试数值的均值,并且曲线c为产生Δ2的相邻2个曲线中数值较小的曲线,则曲线c及以下的曲线d一起会被剔除掉。模拟EXCEL表格画图法算法的优点是可以用软件编程实现,处理速度快;缺点是不同参数的比值百分比难以确定。该算法是利用VBA语言[3]编程实现,软件界面形式见图3。

图3 模拟EXCEL表格画图法软件界面
3.2 一致性剔除离散算法
某参数的一致性等于圆片内所有合格芯片在规定频点的同一个参数的数据最大值和最小值之差的一半,如幅度一致性ΔA =(Gmax-Gmin)/2,相位一致性ΔФ =(Фmax-Фmin)/2。首先设定某个参数在某个频点的一致性范围值,如果一致性计算值超出一致性设定值,则需要剔除。如何以最优方式剔除超出一致性值范围的数据,而使剩余的芯片个数最多,具体有迭代编程计算法、中位数计算法两种实现方法。
迭代编程计算方法为:计算所有合格数据的均值、最大值和最小值,比较最大值和最小值与均值的差值,差值大的优先被剔除掉。每剔除一个数据,重新计算均值、最大值和最小值,再重新比较、剔除,如此循环迭代,直至该频率点计算的一致性值在限定值范围内。
中位数计算方法为:把规定频率点的测试数据按大小顺序排序,选取居中的一个数为中位数(若数据个数为偶数时,则取居中两数的平均值为中位数)。选取中位数的好处是不会受到测试数据中过大或过小数据的影响,例如:设测试的一组数据按大小排序为:2、7、88、88、88、88、88、95;则中位数的值为88。有了中位数和一致性设定值,就可以确定符合规定频点的一致性范围的上限和下限,从而将超出上、下限范围的离散数据剔除掉,如图4所示。
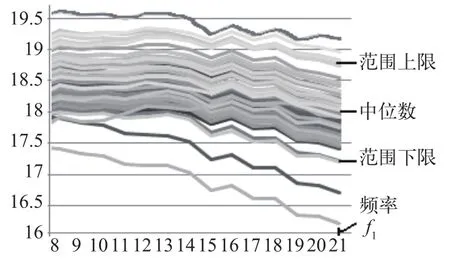
图4 中位数一致性计算法示意图
寻找中位数需要排序,花费的计算时间比循环迭代多。若数据量不是很大(小于千只)时,选择中位数计算法进行离散数据剔除;若数据量很大(大于千只)时,选择迭代编程计算法。一致性计算法剔除离散方法的优点是计算公式简单、软件实现比较容易,大批量测试的生产版的各个参数一致性值一般相对固定;缺点是对于研发版的参数一致性值往往难于确定,另外,通过一致性计算法剔除离散数据有时剔除得不够干净,仍存在个别离散大的曲线。该算法也是利用VBA语言编程实现,软件界面形式见图5。
图5 一致性剔除离散算法软件界面
3.3 累积均方差剔除离散算法
一个圆片的所有芯片的某一测试参数存在明显的主包络,也就是说,固定参数的测试数据分布遵循正态分布,根据统计学理论,如果μ为测试数据的均值,σ为测试数据的方差值,则对于正态分布随机变量来说,其值落在区间[μ-3σ,μ+3σ]的概率为99.7%,即所谓的“3σ规则”[4],如图6所示。根据这个规则,可以计算某一个测试参数的均值和方差,通过数学迭代的方法去除3σ以外的数值,从而使得每一个频点的数据都满足μ±3σ,这就是均值、方差剔除离散的原理,该方法示意如图7所示。

图6 正态分布曲线
均值和方差剔除离散算法从统计学意义上剔除的是小概率的离散数据,保留了小概率的主包络数据,虽然迭代过程花费计算时间,但计算公式成熟,易编程实现。均值和方差剔除离散算法的主要缺点是,计算均值和方差时是对所有数据的计算,离散大的数值会影响到均值,当计算结果满足μ±3σ时,仍有个别离散大的数据没有被剔除掉,如图8所示。累积均方差算法能有效去除整体偏离多的曲线,但缺点是所有频点的均方差累加增加了控制上下限确定难度,而且均值和方差本身计算方法的缺陷仍然存在。
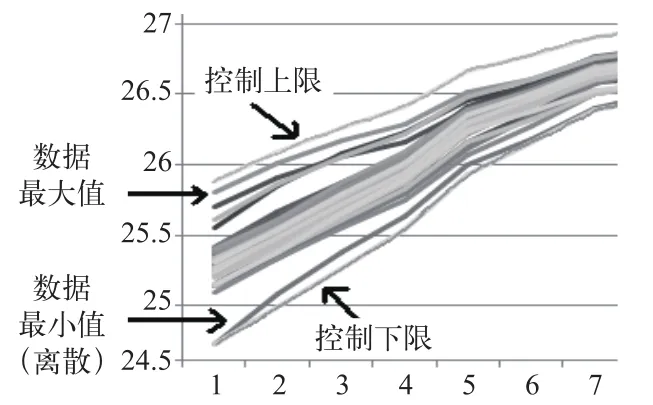
图8 均值和方差算法中没有剔除的离散数据
累积均方差算法是基于均值和方差的方法,它把某一个参数项中同一个芯片中所有频点的均方差累加然后取平均值,这样肯定能最先将整体偏移大的数据剔除掉,而不是首先将个别频率点离散大的数据剔除掉。累积均方差算法是对均值和方差方法的一种优化算法。该算法用C Sharp[5]语言编程实现,软件界面形式为图9所示。
图9 累积均方差剔除离散软件界面
3.4 拟合正态分布曲线算法
假设有一个带有直角坐标的图纸,它的横坐标轴有均匀刻度,代表测试数值,它的纵坐标轴的刻度是不均匀的,表示测试数值出现的概率,则只要在横坐标上等间隔地标上X的值,正态分布函数N(μ,σ2)在直角坐标的图纸上的曲线就成为一条直线。由该正态分布直线与P=50%交点的横坐标读得值为μ,由直线与P=15.9%交点的横坐标读得值为μ-σ,从而可以得到σ的值。由于该正态分布直线是由大多数主包络数据(非离散数据)拟合出来的,因此得到的均值μ和方差σ就有效地避免了离散大的数值影响均值的缺点。再用该方法得到的均值μ和方差σ进行μ±3σ剔除离散数据,得到的结果就比较可信。
具体方法为:将某频点的参数的测试数据按等间隔分组,分组数根据芯片数量来定,在程序中需要人为输入分组数(一般分组数为芯片总个数的10%左右),分组后的数据称为分组数据,每组数据所处的区间端点称为组限,区间中点称为组中值。计算出测试数据落在每个分组数据中的个数,称为组频数,组频数与芯片总个数的比值称为组频率,组频率累加起来构成累积频率;然后进行描点,横坐标为各组的组上限,纵坐标为组上限所对应的累积频率。拟合一条直线,尽量使中间的一些点都落在这条直线上(与直线靠得很近),两端的点允许离直线偏差大一些(两端的离散值会被剔除掉),如图10所示。
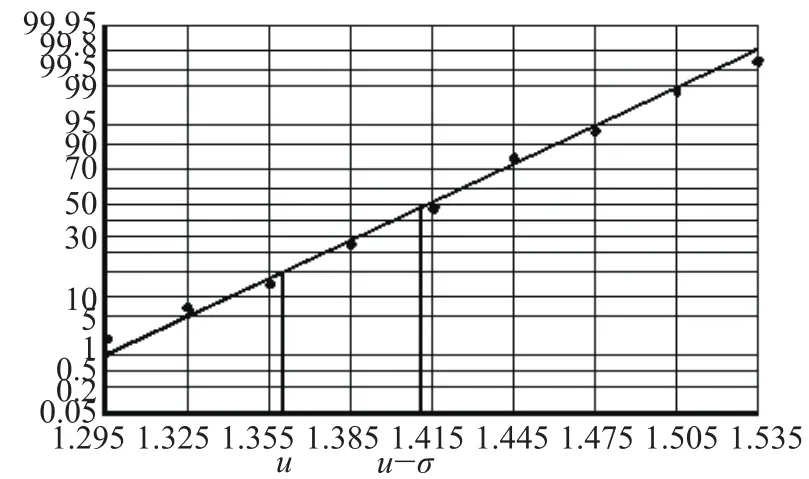
图10 拟合正态分布曲线
拟合正态分布曲线算法用C++语言编程实现[6,7],软件界面如图11所示。拟合正态分布曲线算法的优点是比较可信,基本上不会漏剔除离散数据,控制范围容易确定;缺点是程序中数值排序计算时间多,μ±3σ范围限定迭代程序也要花时间,若处理数据量较大时,该算法的处理速度慢,计算时间长达十几分钟。

图11 拟合正态分布曲线算法软件界面
4 结束语
上述几种算法是作者根据已知理论(一致性计算、3σ规则)或已知思路(EXCEL表格画图)改进、细化得到的,并用软件编程实现,具有独创性和实用性。其中,拟合正态分布曲线算法最为复杂,但经过大量数据验证,漏剔除离散数据的概率最小,所以离散数据剔除采用拟合正态分布曲线算法。把拟合正态分布曲线离散数据剔除算法完善到工艺控制微波数据处理软件,将使微波在片测试数据处理实现自动化。
[1]李效白.砷化镓微波功率场效应晶体管及其集成电路[M].北京:科学出版社,1998:228.
[2]柴海峰,陶雪峰,杜元勋.虚拟仪器与传统ATE联合测试技术研究[J].电子与封装,2010,10(4): 14-16.
[3]姚文涛.Excel VBA应用开发经典案例[M].北京:清华大学出版社,2009:11-43.
[4]浙江大学数学系高等数学教研组.工程数学概率论与数理统计[M].北京:高等教育出版社,1986.118.
[5]刘丽霞,李俊民.C#范例开发大全[M].北京:清华大学出版社,2010.21-113.
[6]蒙祖强,龚涛.C++ Builder程序员成长攻略[M].北京:中国水利水电出版社,2009.65-120.
[7]刘智勇.SQL Server 2008宝典[M].北京:电子工业出版社,2010.300-440.

