一种基于量测伪距的EKF移动长基线AUV协同导航方法
刘明雍, 黄 博, 蔡 挺
一种基于量测伪距的EKF移动长基线AUV协同导航方法
刘明雍, 黄 博, 蔡 挺
(西北工业大学航海学院, 陕西西安, 710072)
在移动长基线(MLBL)定位中, 由于水声信号在水中传播速度较慢, 以及被定位AUV的自身运动, 导致AUV与不同浮标的距离是在不同时间不同位置测量产生的, 所以应用移动长基线会产生一定的时间延迟定位误差。本文针对该定位误差, 提出了一种基于量测伪距的EKF移动长基线时间延迟算法, 该算法利用扩展Kalman滤波, 通过对AUV的位置状态的前推, 重构了系统的量测方程,实现了量测方程同系统的量测量在时间上的一致性, 有效地解决了时间延迟产生的误差。理论分析与仿真结果均表明, 该方法可以显著提高导航定位精度。
自主式水下航行体; 移动长基线; 定位误差; 扩展Kalman滤波
0 引言
导航定位是自主式水下航行器(autonomous underwater vehicle, AUV)发展的关键和制约性问题。它不仅受到AUV自身体积和导航设备的限制, 而且水下环境的特殊性也给AUV导航定位带来诸多的制约瓶颈, 例如水下未知洋流、水声通信受限等。目前水下导航定位方法主要有惯性导航和水声导航。惯性导航短航程时定位精度高, 但长航程会出现累积误差, 导致定位精度降低; 水声导航精度较高, 主要有长基线, 短基线和超短基线方法, 但水声导航方法都需要在载体上安装多个水听器, 在水底布放基阵, 技术操作复杂。
为了降低工程实施难度, 同时进一步提高AUV作业方式和区域的灵活度, 文献[1]首次提出“移动长基线(moving long baseline, MLBL)”的概念, 即通过改进传统长基线技术, 利用无人水面舰船或浮标充当MLBL定位基阵, 通过全球卫星定位系统GPS或其他方式实时获得定位基阵的自身位置, 然后通过基阵之间的探测和定位方程解算, 确定航行器的位置坐标。它与传统长基线系统最大的不同是, 应答器不是固定布设在海底, 而是浮于海面且移动的。文献[2]~文献[5]基于MLBL的概念, 利用最小二乘法算法, 进行了协同定位的试验, 验证了MLBL的有效性。文献[6]针对MLBL定位模型, 设计了扩展卡尔曼滤波(extended Kalman felter, EKF)协同导航算法, 并与几何解方程算法进行了对比, 提高了定位精度。文献[6]同时指出, 在实际应用中, 由于AUV处于运动状态, 同时水声信号在水中传播速度较慢, 由此会产生时间延迟, 在此期间AUV会移动一段距离, 导致AUV定位产生误差。误差大小与海面浮标和被定位AUV之间的距离、被定位AUV的航速有关。距离越远, 航速越大, 则误差越大, 是目前MLBL有待解决的问题之一。
本文详细分析了时间延迟产生的误差, 并提出了一种基于测量伪距的EKF的MLBL时间延迟算法, 可以有效地解决时间延迟产生的误差。
1 MLBL定位原理及模型
图1中, 水面移动浮标布放在海平面上, 至少要3个移动浮标应答器才能得到目标的3D坐标。实际应用中, 一般需要布放4个以上的移动浮标应答器, 以提高定位精度。
系统的定位算法来自于长基线定位算法, 主要有球面相交和双曲面相交法。与长基线基阵固定在海底不同的是, MLBL基阵漂浮在海面上, 通过携带的GPS实时更新自身位置信息。

图1 移动长基线定位原理
MLBL导航定位系统在进行导航定位解算时, 一般按如下步骤进行。
第1步, 按照预定的时间周期, 被定位AUV发送Ping询问信号, 海面上的浮标接收到询问信号后, 通过水声通信装置以不同的频率广播自身的位置信息。
第2步, 被定位AUV接收应答信号后, 通过所用时间可计算出与移动浮标的距离:(为水声在水中传播速度), 从而确定相对位置的几何关系。
第3步, 根据被定位AUV与应答器的相对位置几何关系, 以及接收到的应答器的位置信息, 依照一定的定位算法, 更新自身位置信息, 这就是MLBL导航定位的原理。
通常使用球面相交最小二乘定位算法更新自身的位置信息。因为被定位AUV深度可以通过压力传感器测得, 所以通过3个移动浮标便可测得AUV位置。但为了提高定位精度, 通常都布放4个移动浮标, 采用最小二乘法解算。设AUV位置为(,,), 则定位方程为
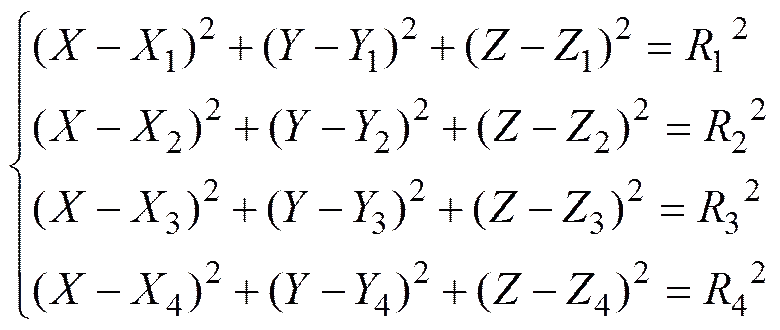
两两相减, 消去二次项,,, 同时深度可通过压力传感器测得
(2)
写成矩阵形式
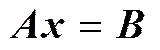
其中
(4)
运用最小二乘法, 可得
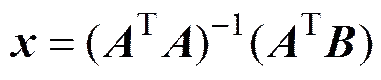
可求得AUV位置坐标。
2 时间延迟误差分析
在应用MLBL的过程中, 被定位AUV处于运动状态下, 且由于水声信号在水中传播速度较慢(1 500 m/s), 因此会产生时间延迟问题。如图2所示, 被定位AUV发送Ping询问信号后到收到浮标的应答信号需要一定的时间。同时由于AUV与每个浮标距离不同, AUV收到每个浮标的应答信号的时间也不相同, 加上AUV的自身运动, 所以AUV是在不同位置不同时间收到应答信号的, 所求R也并非是AUV完全收到应答信号时与各浮标的距离。
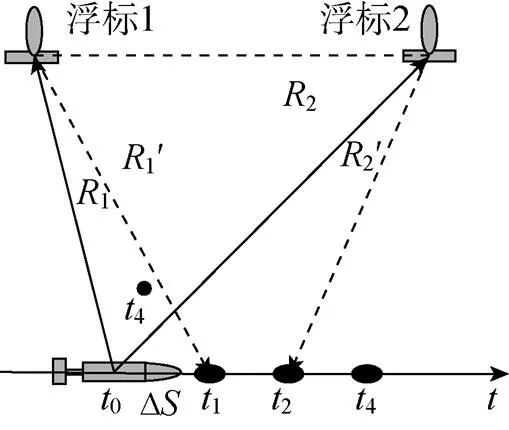
图2 时间延迟误差示意图
对于AUV和浮标1, AUV从时刻发出Ping到收到应答信号所用时为, 其间AUV航行位移为, 由于时间很短,可由航位推算求得, 代入方程(1)中, 得
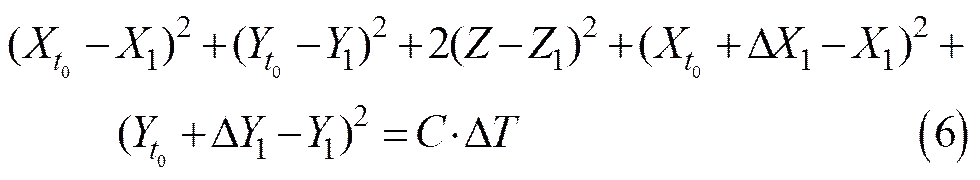
上式简化为
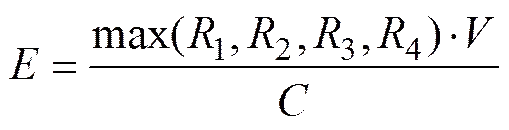
可以看出, 误差大小与被定位AUV和浮标之间的距离及AUV的航速有关, 距离越远, 航速越大, 则误差越大。
3 基于伪距的EKF移动长基线时间延迟算法
3.1 系统方程
AUV运动方程
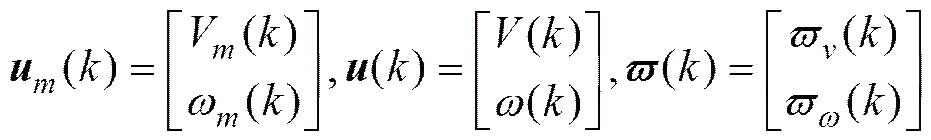
(11)
代入式(9), 运动方程可简写为
其中
(13)
根据式(12), 由EKF算法得一步状态预测
预测协方差
(15)
(17)
3.2 重构量测方程
由于水声传播速度较慢及AUV的自身运动, 若由方程(1)作为量测方程, 据上文知, 测量值是AUV在不同时间不同位置与各浮标的距离, 这将造成量测方程和观测量的不匹配, 求得的解是AUV发出Ping时刻的位置, 将产生时间延迟造成的误差, 所以需重构测量方程。AUV在时刻的位置状态可由时刻位置向前推求得
同理可得, AUV在时刻与其他伪浮标的伪距方程, 以作为量测量, 可得EKF的量测方程
(21)
量测方程的雅可比矩阵为
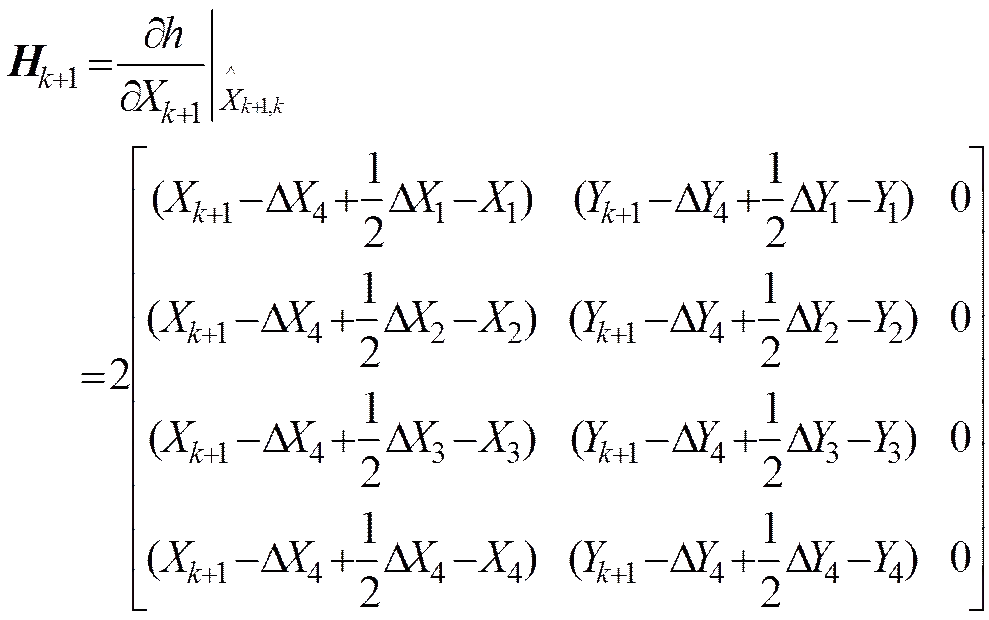
依据EKF公式得
(23)

(25)
(26)
卡尔曼增益为
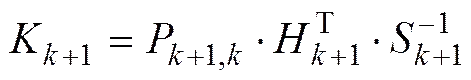
状态更新为
(28)
4 仿真分析
为了验证算法的有效性, 进行仿真分析研究。在仿真试验中, 海面上布放4个浮标, 每个相距5 000 m, 组成正方形基阵。AUV直线航行, 速度为5 m/s, 航向为45°, 深度为-50 m。AUV依据式(1)的运动学模型, 每隔0.2 s采用传统的航位推算更正自身位置状态, 其中速度传感器的测量噪声取为的零均值高斯白噪声, 航向角的测量噪声取为的零均值高斯白噪声, 且速度与航向角的噪声独立且不相关。AUV同时每隔10 s向外发送一次Ping即询问信号, 完全收到各浮标的应答信号后进行定位解算。
本文分别对航位推算, 球面相交最小二乘, 基于测量伪距的EKF算法这3种方法进行对比仿真。由图3可以看出, 被定位AUV单纯运用航位推算算法的位置曲线出现了明显的偏离, 球面相交最小二乘法和基于伪距的EKF算法位置曲线与理想的比较吻合。
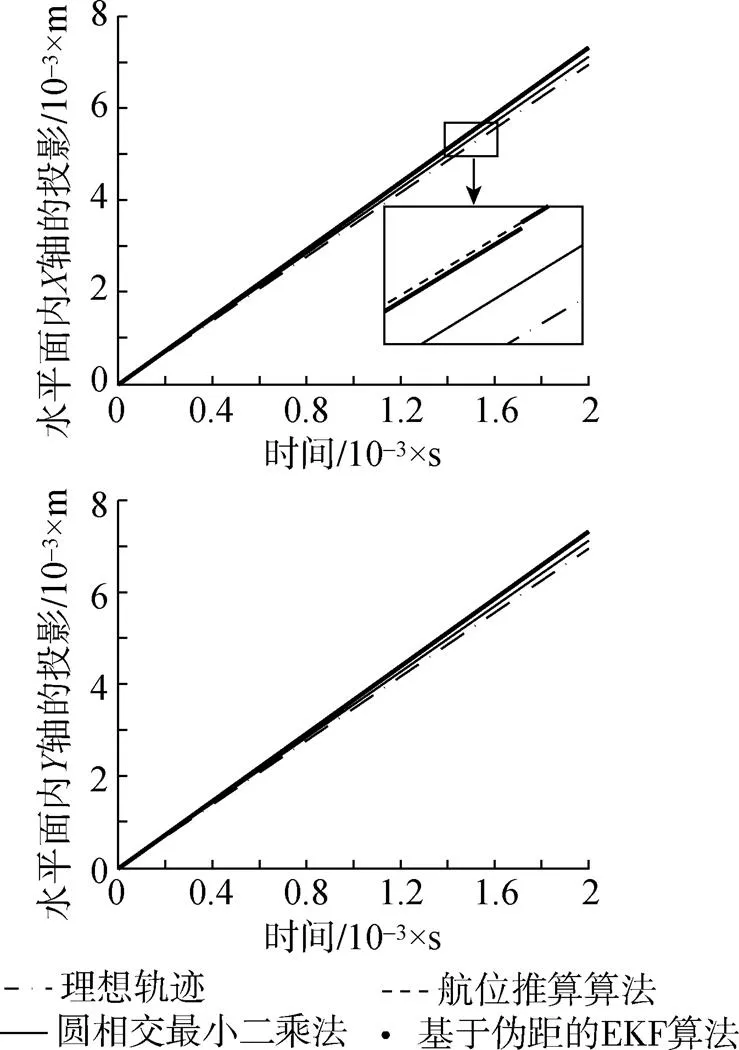
图3 AUV的协同导航轨迹
由图4可得, 当AUV只依赖内部传感器进行推算导航时, 其定位误差不断增大; 当利用长基线球面相交最小二乘法后, 导航精度得到显著提高, 定位误差在50 m内。
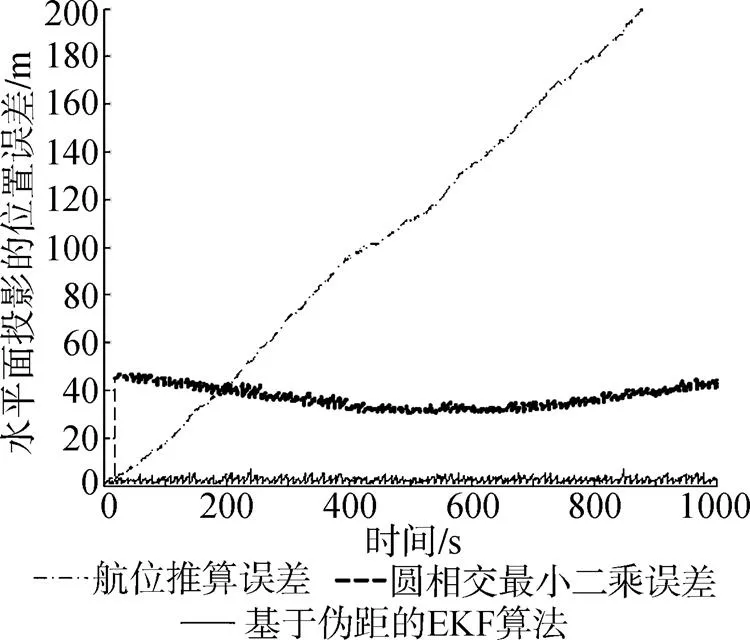
图4 AUV的定位误差曲线
此外, 误差的大小和AUV与4个浮标的几何位置有关, 当AUV航行到600 s时, 位于4个海面移动浮标的中心位置同每个浮标的距离最近, 此时误差最小; 基于伪距的EKF方法误差最小, 大约保持在6m之内, 误差明显小于前2种。仿真结果表明, 改进后的MLBL算法能有效减少由于时间延迟产生的误差。
5 结束语
本文研究了基于海面浮标的AUV的MLBL导航定位方法。重点分析了由于水声传播速度慢和AUV自身运动造成的时间延迟误差。并针对时间延迟误差提出了新的解决方法。主要是利用被定位AUV在一个Ping采样周期内, 航位推算相对精度较高的特点, 通过对位置状态的前推, 重构系统的量测方程, 从而同量测值在时间上匹配, 修正了时间延迟造成的误差。文章最后通过数学仿真, 给出了误差曲线, 验证了算法的有效性。
[1] Vaganay J, Leonard J, Curcio J. Experimental Validation of the Moving Long Base-Line Navigation Concept, in Autonomous Underwater Vehicles[C]//2004 IEEE/OES, 2004: 59-69.
[2] Curcio J, Leonard J, Vaganay J, et al. Experiments in Moving Baseline Navigation Using Autonomous Surface Craft[C]// 2005 MTS/IEEE International Conference on Oceans. Washnigon, PC, USA: IEEE, 2005:730-735.
[3] Bahr A, Leonard J, Fallon M. Cooperative Localization for Autonomous Underwater Vehicles[J]. The International Journal of Robotics Research, 2009, 28(6): 714-728.
[4] Bahr A.Cooperative Localization for Autonomous Underwater Vehicles[D]. Massachusetts Institute of Technology and Woods Hole Oceanographic Institution, 2009.
[5] Baccou P, Jouvencel B, Creuze V, et al. Cooperative Positioning and Navigation for Multiple AUV operations[C]//Oceans'01 MTS/IEEE Conference and Exhibition, Honolulu, 2001: 1816-1821.
[6] 张立川, 徐德民. 基于移动长基线的多AUV协同导航[J].机器人, 2009, 40(4): 794-799.Zhang Li-chuan, Xu De-min. Cooperative Navigation of Multiple AUVs Using Moving Long Baseline[J]. Robot, 2009, 40(4): 794-799.
[7] 田坦. 水下定位与导航技术[M]. 北京: 国防工业出版社, 2007.
(责任编辑:杨力军)
A Cooperative Navigation Method of EKF Moving Long Baseline for AUV Based on Pseudo-range Measurements
LIU Ming-yong, HUANG Bo, CAI Ting
(College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China)
Moving long baseline(MLBL) localization of an autonomous undersea vehicle(AUV) will produce a certain amount of time-delay positioning error due to the slow acoustic signal propagation velocity in water and the movement of AUV itself, which cause differences in time and position in measuring the distances between an AUV and different buoys. In this paper, an extended Kalman filtering(EKF) MLBL time-delay algorithm based on pseudo-range measurement is proposed. In this algorithm, the EKF is adopted to reconstruct the measurement equation of the system via pushing-forward the AUV's position states. So the measurement equation matches with the system measurement in time, and the error from time delay is eliminated. Theoretical analysis and simulation results show that the algorithm can significantly improve the accuracy of navigation and localization.
autonomous undersea vehicle(AUV); moving long baseline; positioning error; extended Kalman filter(EKF)
TJ630.33; TP391
A
1673-1948(2012)06-0432-05
2012-07-30;
2012-09-03.
国家自然科学基金(50979093).
刘明雍(1971-), 男, 博士生导师, 主要研究方向为水下导航、惯性技术及非线性控制.

