一种鱼雷多目标跟踪数据关联方法
杨向锋, 杨云川, 郭 磊
一种鱼雷多目标跟踪数据关联方法
杨向锋, 杨云川, 郭 磊
(中国船舶重工集团公司第705研究所, 陕西西安, 710075)
多目标跟踪是未来鱼雷发展的重要方向之一, 数据关联是实现多目标跟踪的基本前提。鱼雷多目标跟踪的过程表现为一个动基座时变过程, 本文利用鱼雷导航定位和航行姿态参数以及鱼雷检测到的目标信息, 通过坐标变换实现观测空间配准, 通过在统一时钟下实时计算采样周期实现观测时间配准。利用目标大地坐标系3D坐标和多普勒速度构造4D坐标系, 以模糊归一化的4D欧氏距离作为关联法则, 提出了一种适用于鱼雷多目标跟踪的数据关联方法, 仿真试验证明了该方法能有效实现鱼雷多目标跟踪数据关联, 具有一定的工程应用价值。
鱼雷; 多目标跟踪; 空间配准; 时间配准; 关联法则
0 引言
数据关联是多目标跟踪中最复杂的问题之一, 是实现多目标跟踪的基本前提。数据关联处理的正确与否直接影响跟踪精度与航迹质量, 错误的数据关联将导致正确航迹的丢失和错误航迹的剧增。典型的数据关联方法包括: “最近邻”法、航迹分裂法、概率数据关联法、联合概率数据关联法以及各种改进的次优联合概率数据关联法等。数据关联经过多年的发展取得了许多成果, 但主要是应用于雷达、导弹及声纳领域, 鱼雷多目标跟踪及数据关联方法研究目前处于起步阶段, 研究成果不多。
多目标跟踪是未来鱼雷发展的重要方向之一, 其主要任务是通过对多目标的多次观测实现对目标运动状态轨迹及运动参数的估计。
鱼雷多目标跟踪属于典型的“单传感器多目标跟踪(single-sensor multiple-target tracking, SMT)”, 其数据关联属于动态数据关联中的观测与航迹关联, 需要将新观测与已知目标航迹关联, 以确定新观测是已知目标当前航迹、新目标或者虚警。
本文主要研究主动声自导鱼雷多目标跟踪数据关联问题, 根据主动声自导鱼雷的多目标特点和鱼雷工作特点, 提出了一种适用于工程且易于实现的数据关联方法, 较好地实现了鱼雷多目标跟踪数据关联。
1 问题描述
1.1 鱼雷多目标特点
主动声自导鱼雷的主要打击目标是潜艇, 潜艇作战一般是单艇隐蔽作战, 很少出现多艘潜艇编队的情况。潜艇一般都装备多种对抗鱼雷的干扰器材, 包括悬浮式声诱饵、自航式声诱饵、自航或拖曳式尺度声诱饵等。潜艇受到鱼雷攻击时, 在机动规避的同时会释放各种对抗器材诱骗、干扰鱼雷, 消耗鱼雷航程达到逃生的目的, 因此鱼雷攻击潜艇时会出现潜艇与各种对抗器材共存的现象, 在一定时间及空间范围内表现为多目标。潜艇在发现来袭鱼雷时, 布放或释放完对抗器材后, 会进行机动规避, 到达安全距离后对抗器材才开机工作, 因此鱼雷面对的多目标在空间上是“稀疏”的, 而且各种对抗器材与潜艇一般向不同方向运动, 不会出现航迹交叉现象。
1.2 鱼雷工作特点
主动声自导鱼雷通过发射声信号并接收目标反射信号(对抗器材模拟的反射信号)对目标进行检测和参量估计, 获得目标相对的空间信息后进行弹道机动, 实施目标跟踪。由此可见, 作为“传感器”的鱼雷一直处于高速机动状态。在作战过程中, 鱼雷高速机动, 目标同时也处于运动中, 鱼雷与目标的相对位置不断变化, 鱼雷会根据与目标的距离实时调整探测波形和检测周期, 同时鱼雷进行弹道机动时需要一定的时间实现, 最终导致鱼雷的观测周期处于变化之中。综合以上两方面的因素, 鱼雷跟踪目标的过程表现为一个动基座时变过程。
1.3 鱼雷观测的空间配准
基座运动导致鱼雷的多次观测参考系不同, 必须将多次观测置于同一个空间坐标系才能进行数据关联。
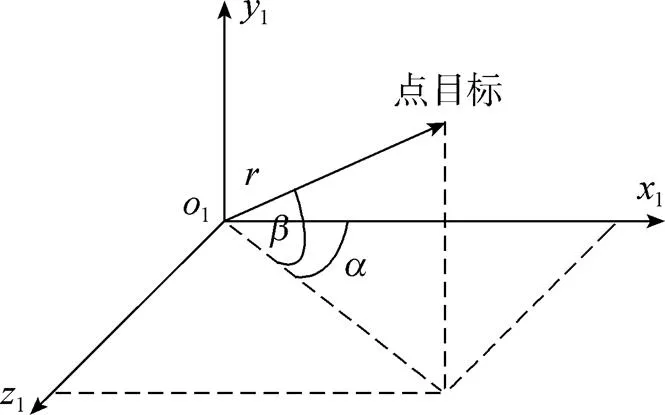
图1 鱼雷直角坐标系
由几何关系知, 鱼雷坐标系的坐标计算公式
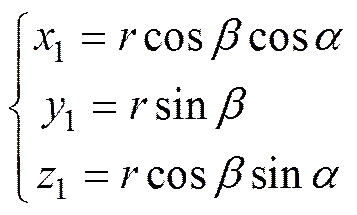
定义为大地坐标系, 原点为发射点,轴垂直向上,轴为发射方向,轴垂直于平面并符合右手坐标系; 鱼雷作为一个具有6自由度的刚体, 其坐标系相对于大地坐标系的位置就由6个坐标来确定, 即鱼雷坐标系原点在大地坐标系中的坐标和鱼雷坐标系与大地坐标系之间的3个夹角。3个角度分别表示鱼雷的偏航角、俯仰角和横滚角, 偏航角从尾部看向左为正, 俯仰角从尾部看向上为正, 横滚角从尾部看向右为正。
鱼雷坐标系与大地坐标系的旋转关系如图2所示。
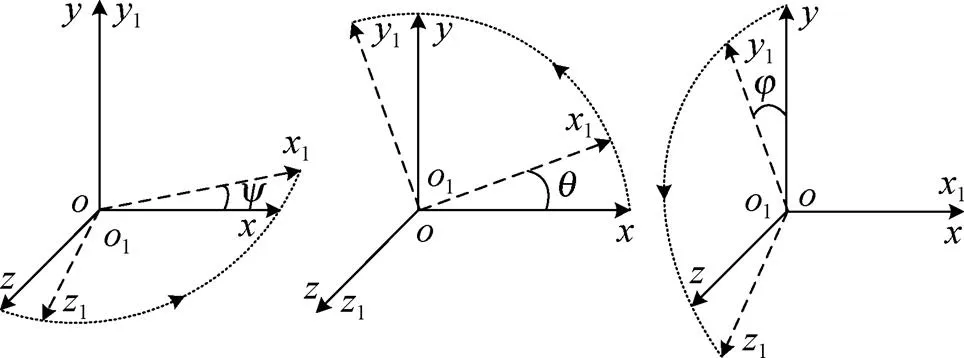
图2 鱼雷坐标系与大地坐标系的旋转关系
由几何关系可知, 鱼雷坐标系到大地坐标系的旋转转换矩阵为
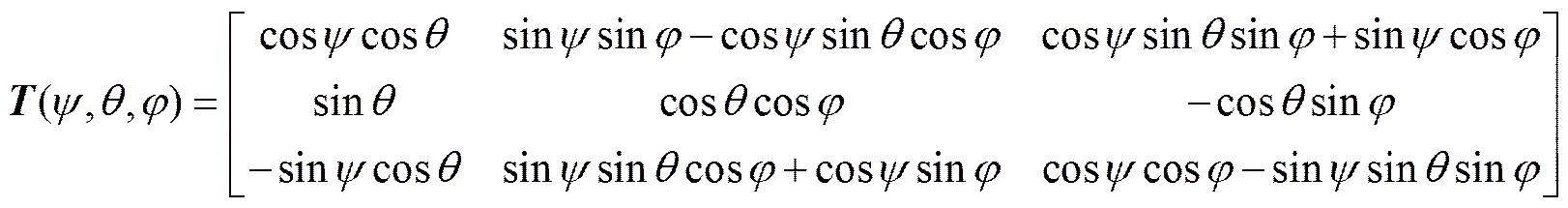
(3)
1.4 鱼雷观测的时间配准
鱼雷攻击目标的过程是一个时变过程, 相邻两次检测之间可能存在鱼雷弹道的机动过程, 同时根据鱼雷自导系统配置可能存在检测周期调整。数据关联需要将当前观测值与航迹的预测值进行关联计算, 如果使用上一次观测时间间隔进行航迹预测, 而本次观测时间间隔不同于上次的观测时间间隔, 就会出现时间失配问题, 导致关联错误。
鱼雷自导系统可以在统一时钟下提供每次检测的精确时间, 观测时间间隔可以通过相邻两次观测的时间进行实时计算, 即
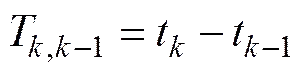
2 数据关联算法
“最近邻”法计算量少, 易于工程实现, 但是太依赖于关联波门, 波门设计依赖于观测误差、观测周期、观测距离、目标机动性和预测误差等, 一个合理的关联波门并不容易获得。概率数据关联法适用于单目标跟踪问题, 假设所有的回波都可能源于目标, 只是概率不同。航迹分裂法和联合概率数据关联法综合考虑了落入波门内的所有点迹, 根据新点迹进行航迹分裂或计算不同排列组合的联合概率, 其优势在于密集多目标处理, 但是两种方法都存在模型复杂且计算量大的特点, 难以应用于计算资源有限的鱼雷。
本文根据鱼雷多目标“稀疏”及不交叉的特点, 提出一种适用于鱼雷多目标跟踪数据关联方法。
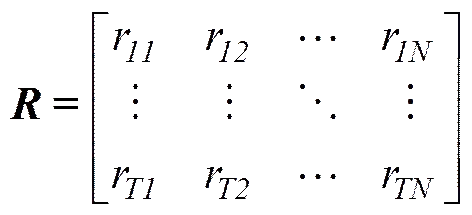
对主动声自导鱼雷而言, 除了可以获得目标在大地坐标系的坐标以外, 还可以获得目标的多普勒速度(多普勒频移)。对真实目标而言, 多普勒速度反映了鱼雷与目标相对速度关系。对干扰器材而言, 多普勒速度很可能是通过人工设定的方式施加到模拟反射回波中, 即使是自航式对抗器材, 其速度与真实目标也存在差异。因此短时间内同一个目标的多普勒速度具有一定的一致性, 不同目标的多普勒速度具有一定的差异性。
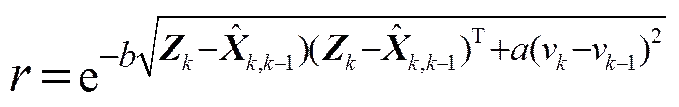
当多目标在空间相距较远时, 关联法则中起主要作用的为多目标的位置信息, 当多目标在空间相距较近或者在目标附近位置出现虚警时, 多目标位置信息出现模糊, 此时多普勒分量将有效提高数据关联的性能, 降低错误关联的可能。
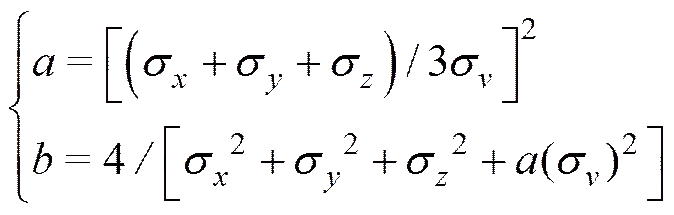
获得关联矩阵后开始进行配对处理, 在关联矩阵中搜索最大关联值, 判断, 满足则第号航迹与第号点迹的关联, 然后删除关联矩阵的第行与第列, 继续对其他可能存在的关联进行搜索, 直至关联矩阵元素为空; 不满足则说明该关联矩阵中不存在关联的点迹和航迹, 直接结束搜索。完成搜索后, 要进一步对未关联成功的点迹和航迹进行处理, 未关联成功的点迹按新目标对待, 未关联成功的航迹进行航迹保持, 即以预测值作为观测值进行航迹更新。
(8)
在实际工程应用中, 要对航迹数和点迹数进行限定, 对于鱼雷多目标跟踪而言, 一般取即可。点迹数达到上限时可按一定规则(如幅值)选取前10个点迹, 当航迹数达到上限时, 新目标做删除处理。航迹连续3拍以上无关联点迹时航迹终止。
3 仿真试验与分析
假设鱼雷总是能可靠检测到目标及各种对抗器材, 无虚警或漏检。仿真场景为鱼雷以 20 m/s沿轴直行, 水平面(平面)内共有3个航迹无交叉的目标, 1号为悬浮式声诱饵, 2号为潜艇, 3号为自航式声诱饵, 目标均等效为点目标, 目标初始位置及状态参数见表1, 其中表示多普勒速度。
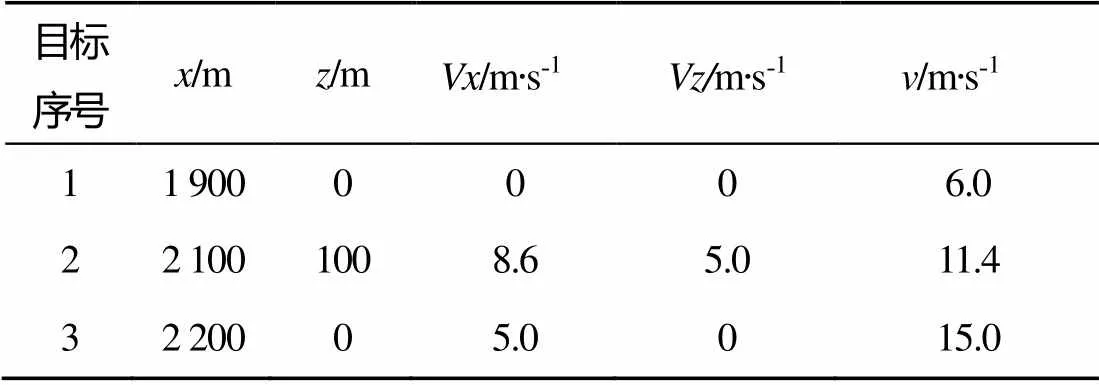
表1 目标初始位置及状态参数
仿真场景模拟了鱼雷典型多目标态势, 目标发现来袭鱼雷后先在航路布放一个悬浮式声诱饵, 一段时间后布放一个自航式声诱饵沿原航路运动, 目标机动规避, 此时目标与2个对抗器材共存, 对鱼雷而言表现为多目标。悬浮式声诱饵多普勒为设定值为6 m/s, 目标和自航式声诱饵多普勒为理论值。
数据样本为理论计算值加入高斯白噪声合成。采样间隔为3 s加入方差为0.5 s高斯白噪声, 模拟观测时变; 目标坐标观测值根据采样间隔计算得到的理论值加入方差为10 m的高斯白噪声, 多普勒速度加入方差为0.5 m/s的高斯白噪声, 模拟观测误差。计算关联值时取,, 数据关联门限。仿真结果如图3~4所示。
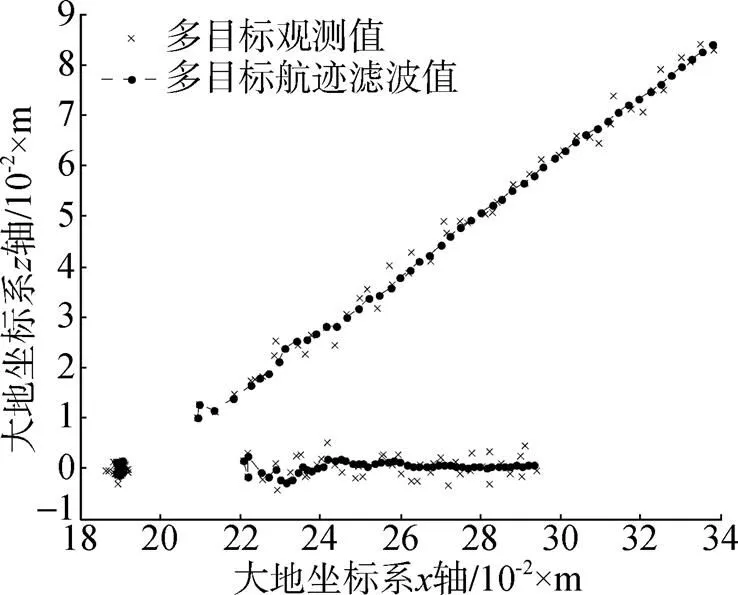
图3 多目标航迹滤波结果
仿真结果表明, 3个目标经过多目标数据关联后形成3条航迹, 关联的航迹与点迹关联值收敛较好, 非关联的航迹与点迹关联值等呈发散状态, 二者区别明显, 关联门限易于选取, 数据关联结果正确, 方法有效。
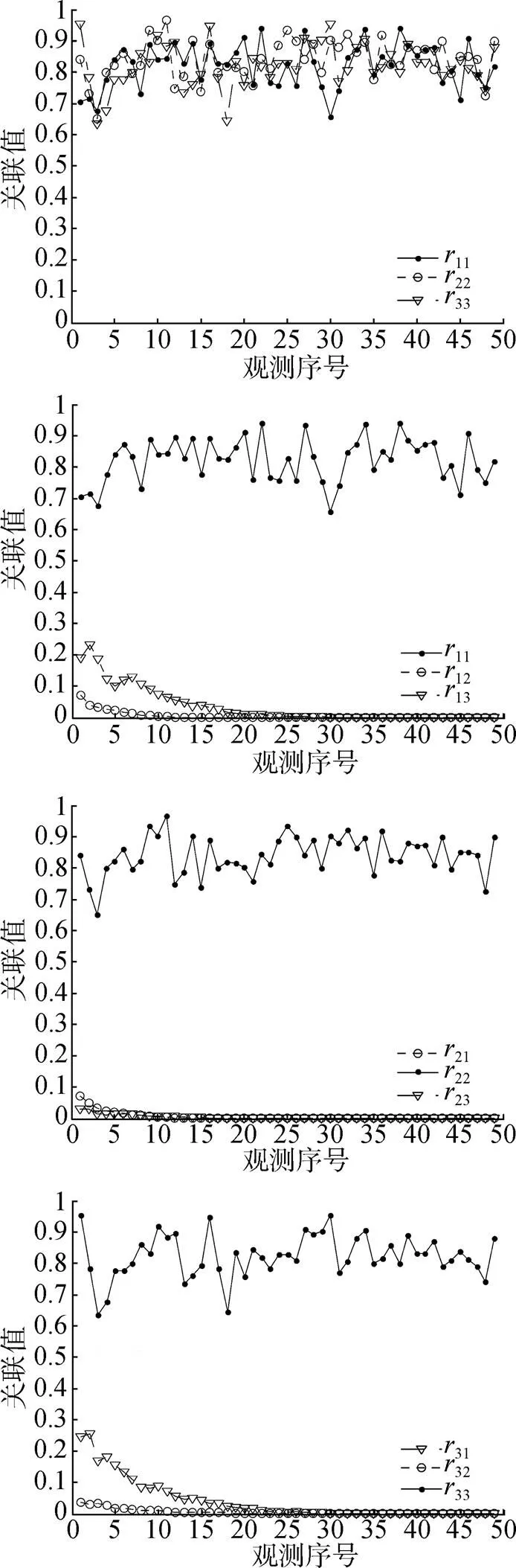
图4 数据关联结果
4 结束语
本文分析了主动声自导鱼雷工作特点及其多目标特点, 提出了一种适用于工程且易于实现的数据关联方法, 首次实现了鱼雷多目标跟踪的数据关联, 仿真试验初步证明了该方法的有效性, 具有一定的工程应用价值。本文是对鱼雷多目标跟踪数据关联的初步探讨, 为鱼雷多目标跟踪数据关联提供了一个思路, 而实际工程中不可避免的存在虚警、漏检等问题, 同时在航迹起始阶段预测误差较大, 因此鱼雷多目标跟踪数据关联问题有待在实际应用中进一步研究。
[1] 权太范. 目标跟踪新理论与技术[M]. 北京: 国防工业出版社, 2009.
[2] 汤军, 孙伟. 弹道目标跟踪的自适应多维分配相关算法[J]. 弹道学报, 2011, 23(2): 72-75.
Tang Jun, Sun Wei. Adaptive Multi-dimension Assignment Algorithm for Tracking Ballistic Target[J]. Journal of Ballistic, 2011, 23(2): 72-75.
[3] 康莉, 谢维信, 黄敬雄. 一种基于蚁群算法的多目标跟踪数据关联方法[J]. 电子学报, 2008, 36(3): 586-589.
Kang Li, Xie Wei-xin, Huang Jing-xiong. ACA Based Data Association Method for Multi-target Tracking[J]. Acta Electronica Sinica, 2008, 36(3): 586-589.
[4] 景晓军, 陈永光. 利用目标多普勒频率的数据融合关联算法[J]. 系统工程与电子技术, 1999, 21(7): 66-68.
Jing Xiao-jun, Chen Yong-guang. Association Algorithm of Data Fusion Using Doppler Frequency of Targets[J]. Systems Engineering and Electronics, 1999, 21(7): 66-68.
[5] Wang X Z, Musicki D, Ellem R, et al. Enhanced Multi-target Tracking with Doppler Measurements[C]//Processing of Information, Decision and Control, 2007: 53-58.
[6] 王润生. 信息融合[M]. 北京: 科学出版社, 2007.
[7] 严卫生. 鱼雷航行力学[M]. 西安: 西北工业大学出版社, 2005.
(责任编辑: 杨力军)
A Data Association Method for Torpedo Multiple-Target Tracking
YANG Xiang-feng, YANG Yun-chuan, GUO Lei
(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China)
Multiple-target tracking is one of the important aims in torpedo development, while data association is a basic for the multiple-target tracking. The torpedo multiple-target tracking process registers as a time-varying process of moving base. In this paper, the parameters of localization and running attitude from torpedo navigation system, as well as the target information detected by a torpedo, are utilized to achieve spatial registration via coordinate transformation. The sampling time is calculated in real time and same clock to achieve temporal registration. The Doppler velocity and the geodetic coordinates of target are used to construct four-dimensional data association coordinates. Normalized fuzzy Euclidean-distance is taken as an association rules. So a data association method for torpedo multiple-target tracking is proposed. Simulation result shows the validity of the proposed method.
torpedo; multiple-target tracking; spatial registration; temporal registration; association rules
TJ630.34; TN911.72
A
1673-1948(2012)06-0414-05
2012-02-04;
2012-03-06.
杨向锋(1978-), 男, 硕士, 高级工程师, 研究方向为水声信号与信息处理, 水下目标识别, 跟踪及水声反对抗.

