一种扩展水下扩频信号多普勒容限方法

苏建军1,2, 冯西安1, 白晓娟1, 李志伟1,2



一种扩展水下扩频信号多普勒容限方法

苏建军, 冯西安, 白晓娟, 李志伟

(1. 西北工业大学航海学院, 陕西西安, 710072; 2. 中国人民解放军91388部队, 广东湛江, 524022)

扩频信号的模糊函数图呈图钉型, 对多普勒频移比较敏感, 影响了扩频信号的使用性能。本文分析了扩频信号的多普勒敏感性问题, 提出了一种基于回波预处理的方法。首先将回波信号经过正交混频得到零中频,通道信号, 然后将零中频,通道信号送入多普勒预处理系统进行处理, 通过时间延迟处理方法得到的2个输出信号, 分别经过匹配滤波器后再进行合并处理, 脉压输出相关函数中不含多普勒频移和时间乘积, 消除了多普勒频移对匹配滤波器输出的影响。数值仿真证明了该方法的有效性, 且具有实现简单, 运算量小的优点。

多普勒容限; 扩频信号; 模糊度函数; 匹配滤波器; 预处理系统

0 引言

目前水下自导系统中常用的信号波形有单频脉冲信号、线性调频信号和双曲调频信号, 这些信号形式简单, 系统易于实现。但是, 由于这些信号的时间带宽积小, 信号形式单一, 易于被敌方的侦察机截获。一旦信号被敌方截获, 水下自导系统容易受到敌方的干扰和攻击, 严重影响了水下自导系统的作战效能。为了提升水下自导系统的生存能力和作战效能, 自导系统应该选用具有大的时间带宽积, 低的功率谱密度的复杂波形。

扩频信号具有大的时间带宽积, 低的功率谱密度, 信号波形与噪声信号相似, 具有一定的随机性, 扩频信号具有很强的抗干扰和隐蔽性能。水下自导系统发射波形使用扩频信号可以提高水下自导系统的抗混响、抗多途和低截获性能。但是, 由于扩频信号对普勒频移比较敏感, 随着运动目标速度增大（即多普勒频移的增加）, 匹配滤波器输出响应变小, 严重时自导系统无法检测目标。关于怎样解决相位编码信号对多普勒敏感的问题, 目前已经有很多文献进行了研究, 但是, 这些解决方案还存在不足, 系统实现也比较复杂, 不适合实时性要求高的场合。本文针对扩频信号多普勒敏感问题, 提出一种基于回波预处理的方法, 该方法系统实现简单, 运算量小, 数值仿真证明了该方法的有效性。

1 扩频信号的数学模型和模糊度函数

直接序列扩频信号的数学表达式为

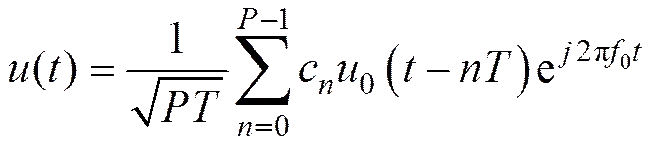
式中:c为伪随机序列;为伪随机序列长度;为子码宽度,,。

根据模糊函数的定义, 直接序列扩频信号的模糊函数为

(3)

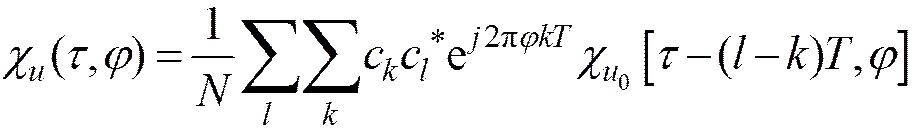
(5)

由式(4)、式(5)可知, 直接序列扩频信号的模糊度函数是由单频矩形脉冲信号的模糊度函数按一定的规律进行时延、频移乘上加权系数后叠加而成, 扩频信号的模糊度图呈图钉型, 具有良好的距离和速度分辨率, 但是, 具有窄的多普勒容限, 不适合检测高速目标。

2 扩频信号的多普勒敏感问题分析

扩频信号对多普勒敏感是因为回波信号受到多普勒频率的调制。若发射信号为s(), 则回波信号为。其中:为回波延迟时间;f为多普勒频率;为发射信号脉宽。匹配滤波器的输出响应为

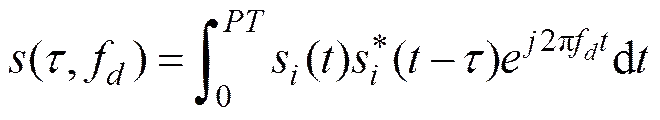
如果, 匹配滤波输出响应

(7)

由式(7)可知, 随着多普勒频率的增大, 匹配滤波器输出响应幅度逐渐变小, 当多普勒频率增大到一定时, 匹配滤波器输出将无法检测到目标。当f<<1/ ()时, 才可以忽略多普勒频率对匹配滤波器输出的影响, 在实际应用中, 只有满足式(8)才可以忽略多普勒频率影响。

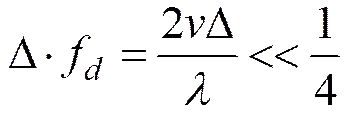
式中:为扩频信号发射脉冲宽度;f为多普勒频移;为目标运动速度;为扩频信号的波长。

图1给出了扩频信号载波频率f=10 kHz、子码宽度=10 µs、伪码长度=1 023的序列, 多普勒频率为f=0.06 kHz,f=0（对应的目标速度分别为8 kn和0 kn）时的匹配滤波器输出响应。

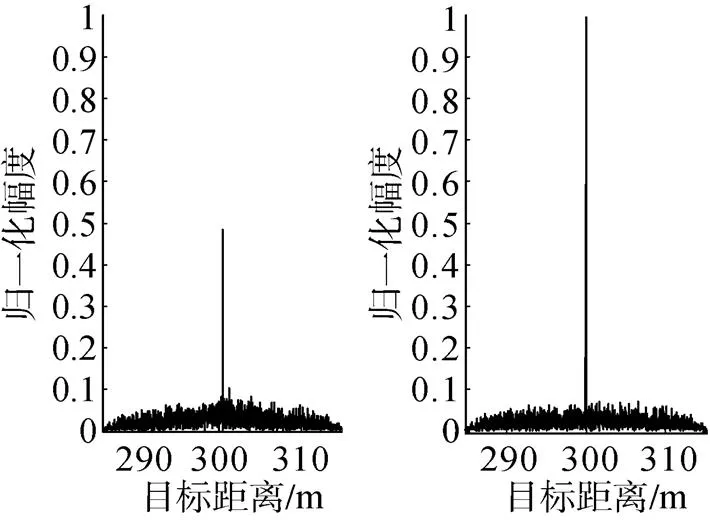
图1 不同多普勒频率时匹配滤波器输出信号

由图1可以看出, 匹配滤波器输出响应幅度随目标运动速度的增加, 峰值的幅度显著减小。当目标运动速度增大到一定时, 就会造成匹配滤波器的失配, 致使无法检测到目标。扩频信号为了能够适应对高速运动目标检测, 就必须设法扩大多普勒容限。

3 基于回波预处理的方法

由式(7)可知, 要减小多普勒频率对匹配滤波器输出响应的影响, 应该设法消除匹配滤波器输出中的多普勒频移与时间乘积项。从这个思路出发, 提出了一种基于回波预处理的方法, 具体步骤如下。

首先, 将回波信号经过正交混频得到零中频,通道信号, 正交混频得到零中频,通道信号的原理框图如图2所示。

设发射信号

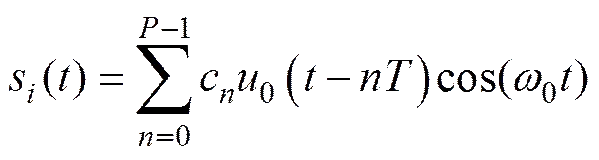
(10)

其中:是回波延迟时间;ω是多普勒频移;是回波信号与发射信号的相位差。

经过正交混频得到零中频,通道信号s()、s()分别为

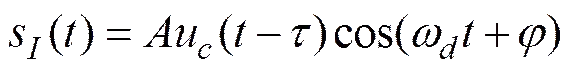
(12)

接着把上一步获得零中频,通道信号s(),s()后送入多普勒有预处理系统进行处理, 多普勒预处理系统框图如图3所示。

则,支路延时后的信号

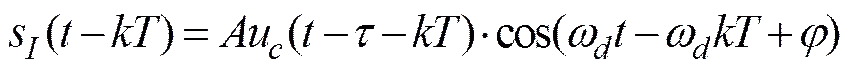
(14)

图3 多普勒预处理系统框图

Fig. 3 Doppler pre-processing system

通过不交叉相乘处理后信号为

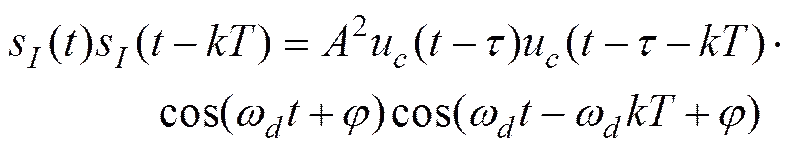
(16)

通过交叉相乘处理后信号

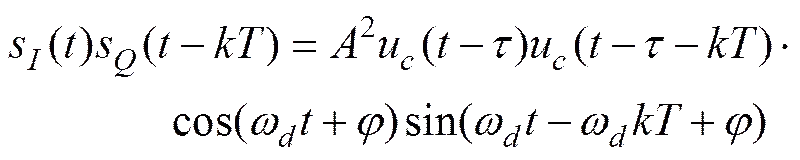
(18)

加法器输出信号

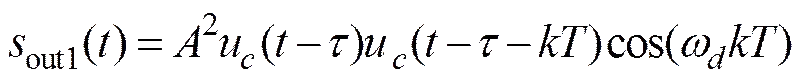
根据序列的移位相乘性, 令

(20)

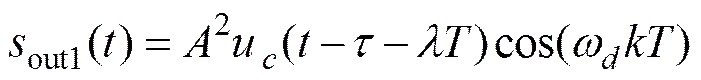
减法器输出信号

(22)

则()最终可简化为

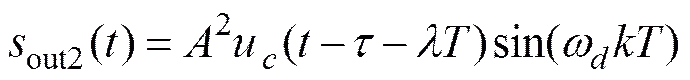
经过匹配滤波器输出响应

(24)

经过匹配滤波器输出响应

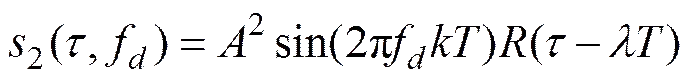
其中

(26)

则回波信号经过匹配滤波器的最后输出

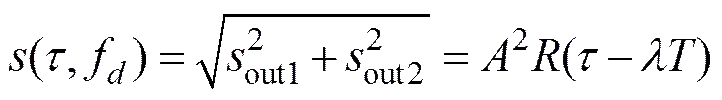
由式(27)可知, 通过对回波信号进行处理之后, 匹配滤波器输出中不含多普勒频移和时间乘积项, 因此, 解决了多普勒频率对匹配滤波器输出的影响。

仿真试验1: 扩频信号的载波频率f=10 kHz, 扩频码选取长=1023的序列, 子码宽为= 10µs, 信噪比为-5dB,=260, 目标速度为=14kn（对应的多普勒频移为100 Hz）, 目标距离为600 m, 仿真结果如图4所示。

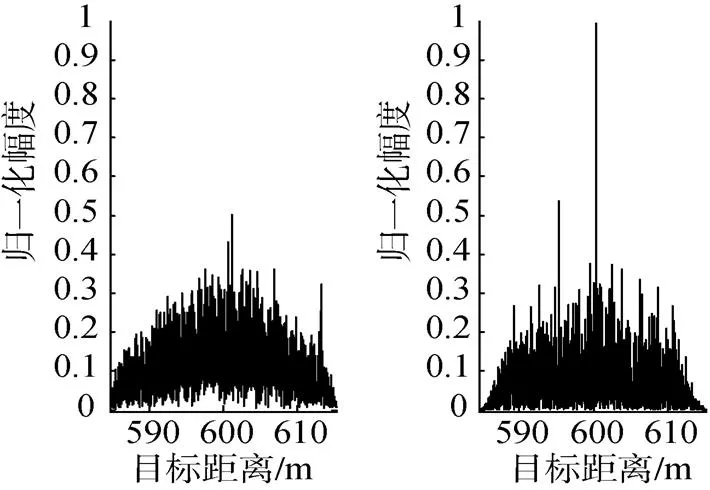
图4 fd=100 Hz(v=14 kn), 距离为600 m时不采用回波预处理方法和采用回波预处理方法的脉压输出

仿真试验2: 信噪比为-15dB, 目标速度为=21 kn（对应的多普勒频移为150Hz）, 其他仿真参数同上, 仿真结果如图5所示。

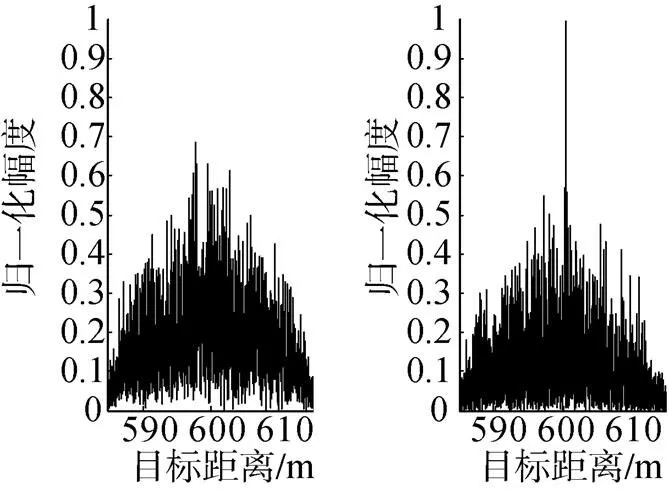
图5 fd=150 Hz(v=21 kn), 距离为600 m时不采用回波预处理方法和采用回波预处理方法的脉压输出

由图4和图5可以看出, 对回波信号没有采取任何措施时, 当目标运动速度很大时, 匹配滤波器输出信号幅度很小, 无法检测到目标。然而, 采取对回波信号进行预处理之后, 因为消除了多普勒频率对匹配滤波器输出的影响, 可以有效地检测高速运动目标。

4 结束语

本文从匹配滤波器输出响应的表达式出发分析了扩频信号对多普勒敏感的原因, 提出了一种基于回波预处理的方法。通过这种方法处理之后的回波信号经过匹配滤波器后, 匹配滤波器输出与多普勒频率无关, 因此扩频信号的多普勒容限得到了极大的改善。该方法系统实现简单, 运算量小, 适合实时处理的场合, 数值仿真证明了该方法的有效性。

[1] 田黎育, 高梅国. 一种二相编码信号多普勒补偿方法的研究与实现[J]. 北京理工大学学报, 2002, 22(6): 757-760.

[2] 孙东延, 陶建锋, 付全喜. 相位编码信号的多普勒补偿[J].空军工程大学学报(自然科学版), 2000, 1(1): 47-49.

[3] 贾鸿志, 朱晓华, 胡庆武, 等. 用补偿式旁瓣抑制滤波器扩展二相码信号的多普勒容限[J]. 信号处理, 1994, 10(3): 187-192.

[4] Park S C, Doherty John F. A Minimax Optimization Approach to Sidelobe Suppression Filter Design[C]//IEEE National Radar Conference, 1996: 3113-3116.

[5] Nathanson F E, Patrick R, Cohen M N, et al. Radar Design Principle-signal Processing and the Environment[C]//IEEE National Radar Conference, 1991: 515-519.

(责任编辑: 杨力军)

A Method for Extending Doppler Tolerance of Underwater Spread Spectrum Signal

SU Jian-jun, FENG Xi-an, BAI Xiao-juan, LI Zhi-wei

(1. College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China; 2. 91388Unit, The People′s Liberation Army of China, Zhanjiang 524022, China)

Spread spectrum signal is sensitive to Doppler frequency shift, which limits the service property of the spread spectrum signal. This paper proposes a method for echo pre-processing by analyzing the sensitivity of spread spectrum signal to Doppler frequency shift. Zero intermediate frequency,channel signals are obtained through the orthogonal frequency mixing of echo. Then the signals are processed in the echo pre-processing system to obtain two output signals by time-delay processing method. The two output signals are further processed by a matching filter to achieve a combined signal which doesn’t contain Doppler frequency shift and time product. Numerical simulation demonstrates the validity of the proposed method with simplicity and smaller amount of computation.

Doppler tolerance; spread spectrum signal; ambiguity function; matching filter; pre-processing system

TJ630.34

A

1673-1948(2012)06-0424-04

2012-04-17;

2012-05-02.

教育部博士点基金(20106102110011).

苏建军(1978-), 男, 在读硕士, 研究方向为水声信号与信息处理技术.