基于遗传算法的足球机器人模糊PID优化控制策略

张小川，魏建新，郭 鲁，吴 杰

(重庆理工大学人工智能系统研究所，重庆 400054)

近年来，国际上流行的机器人足球比赛成为人工智能的标准研究平台之一，是研究多机器人合作与多智能体系统的载体，融合了机器人学、人工智能、模式识别、图像处理、自动控制、通讯、传感等多个学科的知识。目前，国际上有组织的机器人足球比赛有FIRA和RoboCup两大系列，它们最大区别在于FIRA主要是采用集中控制方式来控制足球机器人，RoboCup主要是采用分布式控制方式来控制足球机器人。近年，FIRA也在朝分布式方向发展。足球机器人通常包括视觉、通信、决策和控制子系统，其中控制子系统是其最基本、也是最重要的一环［1］。本文针对FIRA系列半自主型机器人足球比赛，探讨了足球机器人如何提高运动控制性能的问题。

足球机器人运动控制的目的是使之能精确且快速地实现点到点以及任意转角的运动，其控制方法通常采用PID控制、模糊控制等。2种控制方法各有优缺点。笔者查阅到的研究文献通常是将它们作为独立的控制策略加以应用，而没有考虑将它们进行融合使用。因此，本研究尝试将PID控制和模糊控制2种策略相结合，利用遗传算法优化模糊控制规则和隶属度函数，提高FIRA MiroSot足球机器人的运动控制性能。

1 模糊PID控制器原理

1.1 模糊PID控制模型设计

在足球机器人运动过程控制中需要考虑的因素很多，但主要因素是偏差e和偏差变化率ec，其中偏差e是变化的，不同位置偏差e值是不同的。在FIRA MiroSot项目中，基本工作流程如图1所示。

图1 FIRA MiroSot工作流程简图

图1中，足球机器人通过摄像头获取图像信息，在上位计算机(含机器视觉识别系统)处理后获得球场的位置信息，再通过无线信号发送给下位足球机器人(含运动控制器)。上位机与下位机信息交互之后，下位机对球的信息和足球机器人的速度进行模糊决策［2］，依据决策结果对机器人进行实时运动控制，从而实现机器人位移的精确控制［3］。本文的足球机器人模糊PID控制器和工作步骤如图2所示。

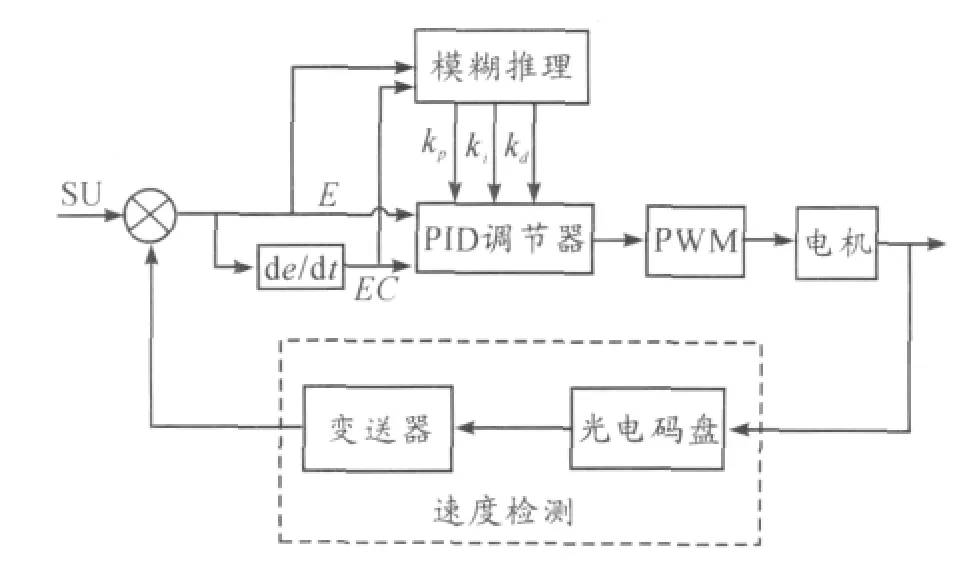
图2 足球机器人的模糊PID控制模型

1.2 模糊PID参数及模糊控制规则设计

通常PID控制器的控制算式为［4］

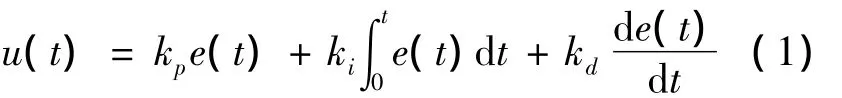
比例系数kp:用于加快系统的响应速度，提高系统的调节精度。kp越大，系统的响应速度越快、调节精度越高，但易产生超调导致系统不稳定;kp取值过小，系统的调节精度和响应速度都会下降，延长调节时间，使系统静态、动态误差特性变坏。

积分系数ki:用于消除系统的稳态误差。ki越大，系统的静态误差消除越快，但ki过大将使响应过程的初期产生积分饱和从而引起较大的超调;ki过小将使系统的静态误差难以消除，影响系统的调节精度。

微分系数kd:用于改善系统的动态特性。在响应过程中抑制偏差向任何方向的交化，对偏差变化进行提前预报。但kd过大会使响应过程提前制动，从而延长调节时间，降低系统的抗干扰性能。

3个参数对整个系统控制精度的影响是相互制约和相互影响的。下面综合考虑系统的稳定性、响应速度、超调量和稳态精度，分析不同的e和 ec对参数 kp、ki、kd调整的规则。

1)当|e|很大时，控制器的输出按最大(或最小)输出，以迅速调整误差，使误差绝对值以最大速度减小，同时，为了防止积分饱和，应取较大kp和较小 kd，ki取零。

2)当e*ec＞0时，误差绝对值朝增大方向变化。应加强控制作用，使误差绝对值朝减小方向变化，这时应取较大kp(但kd不能太大)，同时取较小 ki。

3)当e*ec＜0或e=0时，误差绝对值朝减小的方向变化或已达到平衡状态。此时可保持控制器输出不变。

4)当e*ec=0，e≠0时，系统曲线与理论曲线平行或一致。为使系统具有良好的稳态性能，应采取较大kp和ki值，同时为避免在设定值附近振荡，并考虑系统的抗干扰性能，适当选取kd值。

基于上述考虑，将偏差e和偏差变化率ec作为模糊控制器的输入，PID控制器的3个参数kp、ki和kd作为输出。设定输入变量e和ec语言值的模糊子集为{负大，负中，负小，零，正小，正中，正大}，简记为{NB，NM，NS，Z，PS，PM，PB}。同样，设定输出量 kp、ki和 kd的模糊子集为{NB，NM，NS，Z，PS，PM，PB}。输入输出变量的隶属函数的论域均定为［－6，6］。隶属函数均选为灵敏度高且在论域范围内均匀分布、等距离的三角形函数。kp、ki和 kd的模糊控制规则分别对应于表1～3。

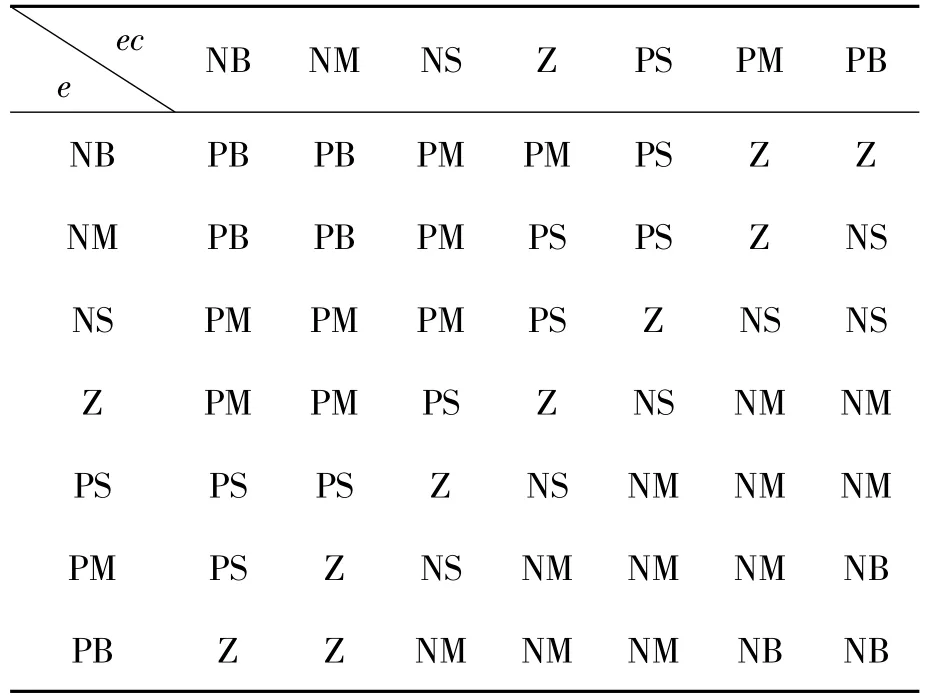
表1 kp的模糊控制规则

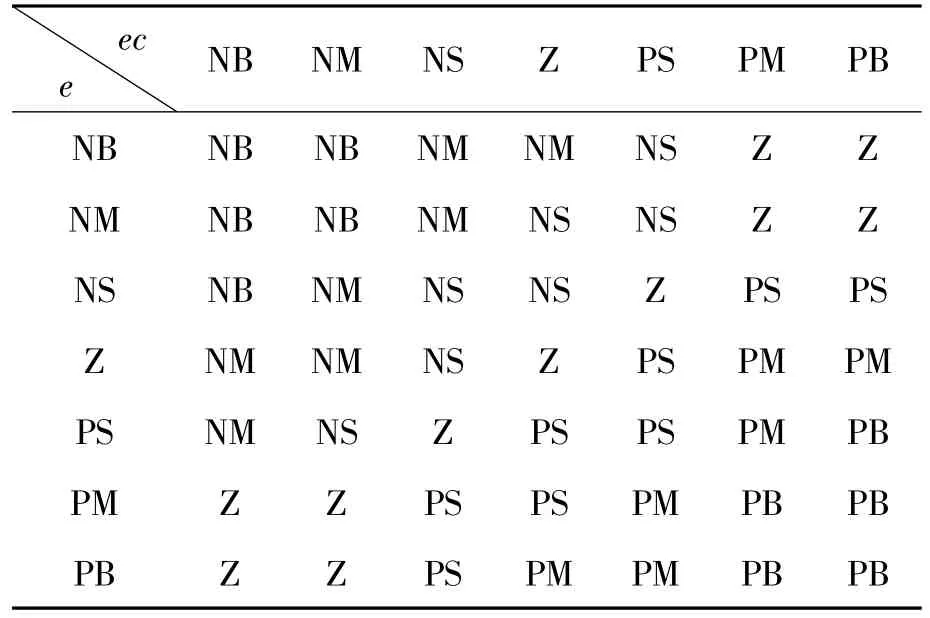
表2 ki的模糊控制规则

表3 kd的模糊控制规则

2 基于遗传算法的模糊PID控制

2.1 遗传算法原理

遗传算法是模仿生物遗传学和自然选择机理，通过人工方式构造的一类优化搜索算法，是对生物进化过程进行的一种数学仿真［5－15］。遗传算法基本思想是:模拟生物系统“适者生存”的原理，通过选择、交叉和变异等简单操作的多次重复来达到优胜劣汰的目的，从而获得问题的最优解。遗传算法的实现由2部分组成:一是编码与解码;二是遗传操作。遗传算法作为较早产生的一种进化算法，对对象模型难于建立、搜索空间非常庞大的复杂问题的优化求解有很强的鲁棒性和全局收敛性。遗传算法流程［16］如图3所示。

2.2 基于遗传算法的模糊PID控制器结构

本文通过遗传算法优化模糊PID控制器中的控制规则和隶属函数来实现对机器人控制系统的优化控制。原理如图4所示。

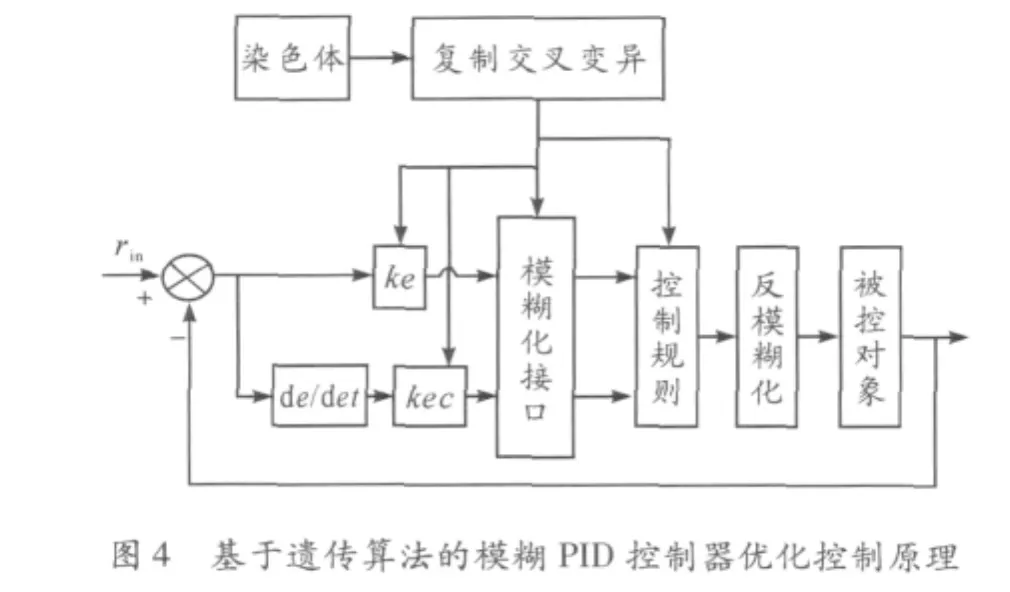
2.3 遗传算法优化隶属度函数

隶属度函数一般根据实验逐步修正取得，很难获得最优。模糊隶属度函数的常见形式有三角型、正态型、尖型和梯型等。本文采用三角型，其模糊隶属度函数可表示为

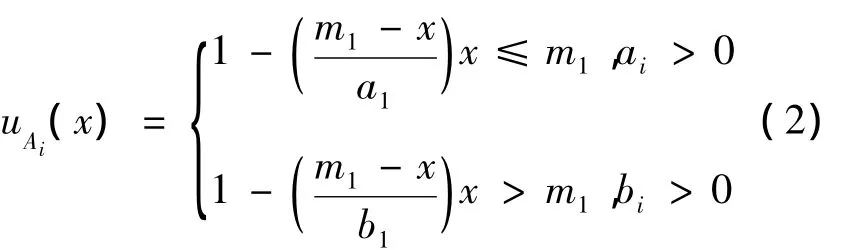
其中(ai，mi，bi)为隶属度函数参数。对n维输入状态(x1，x2，…，xn)，依据规则集合中第 i条规则，其模糊输出的模糊隶属度为:

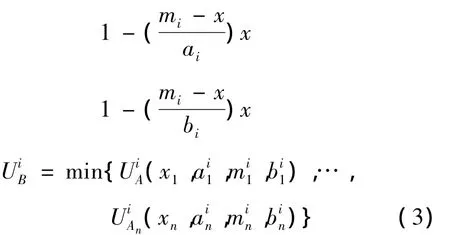
u由隶属函数的参数(ai，mi，bi)和输入状态(x1，x2，…，xn)共同决定。在系统输入变量数目确定的情况下，合理选择隶属函数的参数(ai，mi，bi)可使式(4)中J最小。在式(4)中，yi表示系统实际输出表示系统理想输出。

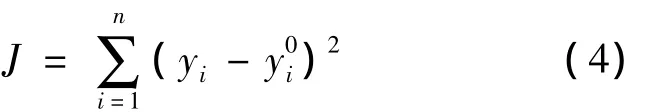
一个模糊控制系统涉及多个模糊变量，每个模糊变量有数个子集，每个子集的模糊隶属函数又有n个参数。因此，对整个系统隶属函数参数优化的问题就转为满足式(2)、(3)约束的J最小值的多维寻优问题。因此遗传算法可以发挥其寻优作用。本文利用遗传算法的寻优步骤为:

1)确定编码方案，以待寻优的各参数编码形成个体。

2)确定各参数的变化范围，建立基因与参数间的一一对应关系。

3)按系统寻优目标，构造适应度函数F。

4)利用遗传算法寻优求解，得到满足系统性能指标的最优隶属函数参数。

2.4 优化模糊PID控制规则

2.4.1 模糊PID控制规则的编码方式

在该系统优化设计中，采用二进制编码［17］字符串来编码。待优化的规则共49条，将每条控制规则用4位二进制数表示，其中第1位为控制位，另3位为规则表示位，然后串接成一条染色体。这样，控制规则经过二进制编码得到的规则染色体是由49位控制基因和3×49位规则基因构成。将前面的模糊语言值{NB，NM，NS，Z，PS，PM，PB}分别用3位二进制数表示为{000，001，010，011，100，101，110}，通过控制基因实现对规则基因的单层控制，即:第1位为“0”代表不起作用，为“1”代表起作用。

2.4.2 体适应度函数F的确定

遗传算法在优化搜索中基本不利用外部信息，仅以适应值函数为依据，利用种群中每个个体的适应度值进行搜索。适应度函数的选取直接影响到遗传算法的收敛速度以及能否找到最优解［18］，这里目标函数采用ITAE积分性能指标

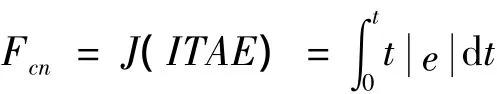
这种目标函数用于控制系统的优化，综合评价控制系统的响应时间、超调量等。由于遗传操作是根据适值大小进行的，且适值是非负的，而目标函数的优化方向应对应于适值增加的方向，所以选用Fcn的负值作为适值函数，即F=－J。

2.5 遗传算法运行参数的确定

运行参数包括群体大小M、遗传代数T、变异概率pm、交叉概率pc等。根据实际情况，本文M=100，T=50，pm=0.008，pc=0.9。

3 仿真实验结果及分析

FIRA MiroSot足球机器人是一个体积为7.5 cm ×7.5 cm ×7.5 cm 的双轮小车，驱动部件为直流电机。为了检验遗传算法模糊PID控制系统的性能，实验中用系统偏差e和偏差变化率ec分别表示足球机器人轮速变化量和轮加速度变化量，并将其作为模糊控制器的输入，进行了大量的仿真实验。下面以一阶时滞系统作为被控对象进行仿真实验。设被控对象为

在速度控制中单一的PID控制与遗传算法模糊PID控制的效果比较如图5所示。从图5中可以看出，遗传算法模糊PID控制系统超调量小、响应快、稳态误差小，性能远远优于传统PID控制。

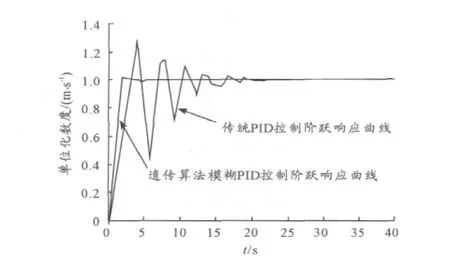
图5 转速控制启动的曲线

4 结束语

本文以FIRA MiroSot足球机器人为研究平台，引进遗传算法，改进了模糊PID控制系统，提高了足球机器人的鲁棒性能。从仿真结果可以看出，引入遗传算法之后的模糊PID控制与常规PID控制相比，控制调节更平稳，控制速度更快。即使在系统控制参数发生变化或扰动时，该控制系统的动态品质劣化程度也较小，克服了系统时滞、非线性等缺点，增强了足球机器人运动系统的准确性和稳定性，缩短了动态调整时间。

［1］高大志.机器人足球，智能机器人的新领域［C］//机器人足球研讨班论文集.沈阳:［出版者不详］，1998.

［2］GAO Yong-yan，FRANK P M.Analysis and synthesis of nonlinear time-delay systems via fuzzy control approach［J］.IEEE Trans on Fuzzy Systems，2002，3(2):200-211.

［3］UDDIN M N，ABIDO M A.Real-time performance evaluation of a genetic algorithm based fuzzy logic controller for IPM motor drivers［J］.IEEE Trans on Ind Applicat，2005，41(1):246-252.

［4］吴全玉，张晓东，晁晓琪，等.基于经典PID算法的智能车系统研究［J］.自动化与仪器仪表，2011(1):25-26.

［5］李祖枢，谢汝林，张小川，等.人工生命体行为选择及其进化研究［J］.模式识别与人工智能，2005，18(3):303-309.

［6］张小川，陈光年.六子棋博弈评估函数的研究［J］.重庆理工大学学报:自然科学版，2010(2):64-68.

［7］边霞，米良.遗传算法理论及其应用研究进展［J］.计算机应用研究，2010，27(7):18-23.

［8］郝艳伟.李祖枢.一种改进的遗传规划算法［J］.重庆理工大学学报:自然科学版，2011(4):74-78.

［9］王越，许全文，黄丽丰.基于改进遗传算法的连续函数优化［J］.重庆理工大学学报:自然科学版，2011(2):62-67.

［10］张勇，王新赛，贺菁.基于遗传算法的战时维修保障力量分配方法［J］.四川兵工学报，2011(2):130-131.

［11］朱文斌，李国林.遗传算法在武器装备保障资源优化中的应用［J］.四川兵工学报，2011(5):85-87.

［12］路彬彬，贾振红，何迪.基于新的遗传算法的模糊C均值聚类用于遥感图像分割［J］.激光杂志，2010(6):15-17.

［13］范巧艳，艾斯卡尔·艾木都拉.遗传算法优化RBF网络的图像杂波抑制技术研究［J］.激光杂志，2010(2):11-13.

［14］刘文涛.基于改进遗传算法的网络入侵检测［J］.重庆工商大学学报:自然科学版，2010(5):476-480.

［15］李宏伟.基于改进遗传算法的电力系统无功优化的研究［J］.自动化与仪器仪表，2011(6):7-11.

［16］周宜今.遗传算法原理及应用实例［M］.北京:兵器工业出版社，2010.

［17］王晶，李玉兰，蔡自兴，等.基于遗传算法的模糊系统优化设计方法［J］.控制理论与应用，1999，16(5):699-704.

［18］马长华，于世海，朱传兴，等.基于遗传算法的模糊控制规则优化的研究［J］.江苏大学学报:自然科学版，2003，24(4):69-73.