空滤器声学性能预测及结构改进

常志权，金 岩

(中国汽车工程研究院股份有限公司汽车噪声振动和安全技术国家重点实验室，重庆 400039)

发动机空气滤清器的主要作用是在空气进入发动机气缸之前对其进行过滤，使进入气缸的空气保持清洁，保证发动机的正常工作［1］。但是作为发动机主要的噪声源之一，进气噪声的改善对降低发动机噪声有着重要的影响，而空滤器作为进气系统的重要消声元件，其消声性能就成了设计时必需考虑的一个重要因素。

边界元法是发动机进排气系统设计中常用的一种方法［2］。它以定义在边界上的边界积分方程为控制方程，通过对边界分元插值离散，化为代数方程组求解，具有解析与数值相结合的特点，通常具有较高的精度。本文基于虚拟分析技术，采用声学分析软件中的边界元分析方法对某款发动机原有的空滤器进行了声学预测分析，并针对其声学性能进行了声学结构改进，以提高其在关注频带内的消声性能。

1 空气滤清器声学性能预测

1.1 边界元法理论基础

本文所用方法为间接边界元方法，故这里仅对间接边界元方法进行阐述。间接边界元法不是用边界的待解边界值作为未知函数，而是在无限大区域内沿着该问题的计算边界配置某种点源分布函数作为间接的待解未知量，它对计算区域的影响是一系列点源影响的叠加［3－4］。由于基本解是自动满足控制微分方程的，因而只要这些间接点源函数在边界各处产生的影响刚好与给定的边界条件一致，则根据定解问题解的唯一性原理，在计算区域范围内和边界上的影响也就是该边值问题的特解。

设待解边值问题的计算区域为Ω，边界为S。要求的解就是既能在区域内满足问题的线性控制微分方程，又能在边界上满足给定的边界条件(在S1上us=，在S2上qs=¯)的特解。设已经有在无限区域中某一点P(源点)上作用1个单位点源的基本解˙u(Q，P)及其一阶导数˙q(Q，P)，其中Q是各个场点。

假设在无限大区域内取一条几何上与原问题边界S完全相同的边界S'，在其上放置一系列点源，其分布密度为φ(P0)，则φ(P0)对域内任一场点Q产生的影响，可利用叠加原理得出如下积分公式:

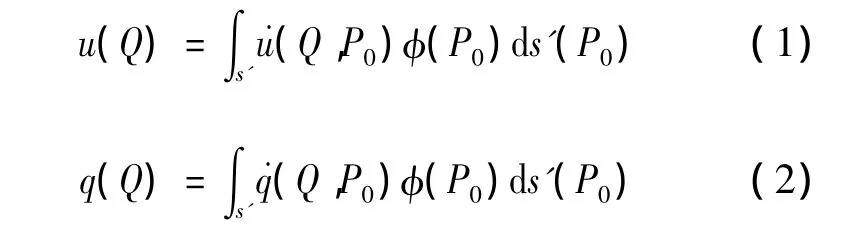
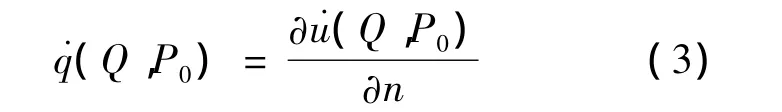
式(3)中n为S'的外法线方向。

如果把场点Q取为边界S'上的Q0点，则有

式中Cu和Cq是在源点P0与场点Q0重合时，由于基本解积分的奇异性引出的共点效应系数，在光滑边界时，其值为0.5或0，视采用哪一种分布源函数φ(P0)而定。现仿照实际边值问题给定的边界条件，在S上要求:

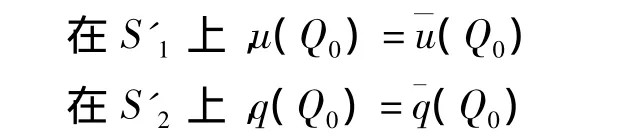
将式(4)、(5)代入，就可以得到以φ(q0)为未知函数在S'1和S'2上的边界积分方程:

根据式(6)、(7)就可确定边界上分布源函数φ(P0)。然后再按式(1)、(2)就可以计算出任一场点Q(包括边界场点Q0)处的函数值u(Q)和q(Q)。

1.2 声学性能预测

图1是根据某柴油发动机空滤器及进气管实物所建的CAD模型。空滤器内部为桶状腔体，底部为一凸台，滤纸紧贴腔体的圆周。通过测试发现，有无滤纸对空滤器1200 Hz以下传声损失影响不大，因此，在建模及优化时，忽略了滤纸的影响。

图1 空滤器CAD模型

图2是空滤器及进气管的边界离散模型，是在图1空滤器及进气管CAD模型基础上，抽取三维模型的内腔壁面作为建模的对象。

图2 空滤器内腔离散模型

确定进气噪声分析的频率范围

式中:n为发动机转速(r/min);τ为冲程系数(四冲程发动机取2);i为汽缸数;k为阶次。本文中发动机最大转速为4500 r/min，为四冲程四缸发动机。考虑到进气噪声的谐次，这里k分别取1、2、3、4。由以上参数确定本文中进气噪声分析的最高频率f=1200 Hz。

为了保证计算结果的准确性，在声学仿真的计算模型里要保证每一单元均要满足:每一声波波长内保证不少于6个单元的原则［5］。据此原则对空滤器的几何模型进行离散，图2的网格模型中，单元大小为10 mm，共划分了2961个单元，2929个节点。

图3是空滤器系统的边界元模型。其中，在空滤器进气管口位置施加能量均匀的白噪声声压边界条件进行声学计算。

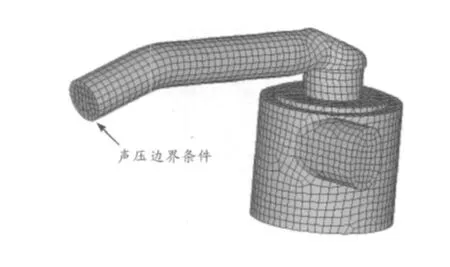
图3 空滤器边界元模型

通常用传声损失来描述空气滤清器的消声性能:

式中P1、P2分别为空滤器进出口处的声压值。

图4中的”simulation”为模拟计算出的空滤器系统的传声损失曲线，即入口处与出口处声压级之差。图4中的“test”为试验测得的空滤器传声损失曲线。通过模拟与试验结果对比可知，声学模型建模可认为是准确的，通过模拟分析的手段进行空滤器声学性能预测是可行的。

图4 原空滤器传声损失曲线

2 空滤器声学结构改进

从图4可以看出，190 Hz和480 Hz频率附近存在通过频率，需进行结构改进。

本文采用常用的共振腔法对空滤器系统进行优化设计。在进气管道加上相应的共振腔进行消声结构设计，共振腔的消声频率为［6］

式中:c为声速;s为共振腔小孔面积;l为孔径有效长度;V为共振腔体积。

式(10)是依据总参数模型得到的。按照式(10)得到的计算结果与通过三维模型计算得到的结果存在一定的偏差。分别针对190 Hz和480 Hz的通过频率，采用边界元法对共振腔的尺寸进行优化设计。综合考虑共振腔的尺寸受到发动机舱内空间的限制，最后得到2个腔体的最佳尺寸分别为:s1=314 mm2，l1=25 mm，V1=1.02×106mm3;s2=251 mm2，l2=20 mm，V2=1.63 ×105mm3。

图5为在进气管道上加上上述尺寸的共振腔后空气滤清器系统的三维模型。图6为对应的边界元计算模型。

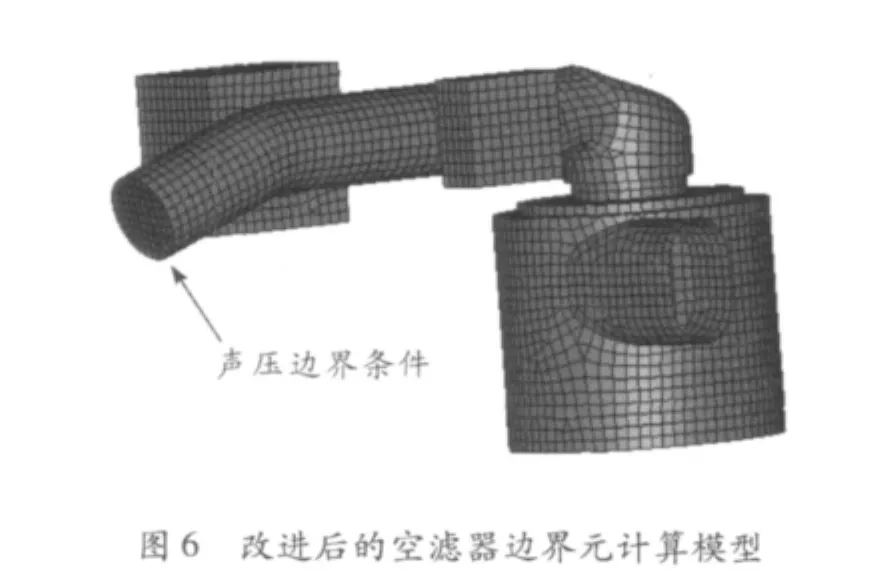
图7中的2条曲线分别为声学结构改进前后的空气滤清器系统传声损失曲线。对比图7中2条曲线可知，增加共振腔后的空滤器在190 Hz和480 Hz附近的消声量明显提高，说明了声学结构改进的有效性。从图7还可以看出，空滤系统在各个频段的消声量都有一定的提高，主要是消声容积的增加所导致的。

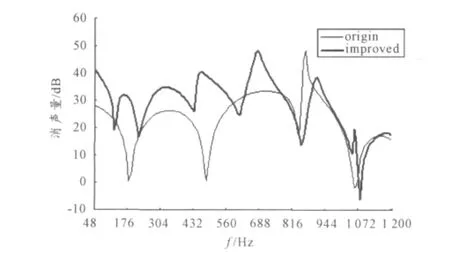
图7 改进前后空滤器传声损失曲线

图8为空滤系统声学结构改进后的传声损失仿真计算与试验结果，验证了仿真计算结果的正确性，再次证明了声学性能预测的可行性。

图8 改进后空滤器传声损失曲线

3 结论

1)采用声学边界元法对空气滤清器系统进行声学预测是准确可行的。

2)采用共振腔对空滤器系统进行声学结构优化的方法是可行的，可对车用空滤器系统的工程应用起到了很好的指导作用。

［1］陈家瑞.汽车构造［M］.3版.北京:机械工业出版社，2009.

［2］Bilawchuk S，Fyfe K R.Comparison and implementation of the various numerical metheds used for caculating transmission loss in silencer system［J］.Applied Acoustics，2003，64:903 －916.

［3］姚振汉，王海涛.边界元法［M］.北京:高等教育出版社，2010.

［4］嵇醒，臧跃龙，程玉民.边界元法进展及通用程序［M］.上海:同济大学出版社，1997.

［5］岳贵平.汽油机进排气系统噪声模拟技术研究［D］.长春:吉林大学，2007.

［6］方丹群.空气动力性噪声和消声器［M］.北京:科学出版社，1978.