双离合变速器中摩擦模型的选择及仿真
杨翔宇,张子川,陈 宝
(重庆理工大学重庆汽车学院,重庆 400054)
双离合变速器(DCT)作为一种新型的变速设备,主要特点是2个离合器交替使用,换挡过程中原挡位还未完全脱开时另一挡位已预先结合,因此具有结合平顺、换挡无动力中断等优点。但由于离合器摩擦片的增多,滑磨状况变得更为复杂,摩擦因数变化对整个离合器性能的影响也随之增大。在以往关于变速器的研究中,以摩擦因数为定值或简单的线性函数为主,但对于双离合变速器,此种方法就不适合。基于此,在对双离合变速器的研究中考虑摩擦模型因素,能使结论更加准确,对于之后变速器仿真模型的完善和实验研究有重要意义。
本文在对双离合器输出扭矩的研究中引入了摩擦效应的概念,建立了相应的扭矩模型和摩擦模型,得到了起步阶段有无摩擦模型影响的整车滑磨功、冲击度曲线,并进行比较。提出按照离合器结合的不同阶段选取不同摩擦模型的研究方法。
1 理论模型的建立
1.1 摩擦现象
磁摩擦是2个接触表面产生切向力的现象,最早的研究是1519年由Leonardo进行的,各种实验和研究已经揭示了许多摩擦特性。目前,已知摩擦与许多因素相关,如相对速度、加速度、温度、材料、位移、润滑情况、接触面状况等。
1)库伦摩擦。库伦摩擦为非零速运动下的摩擦,是最早被发现的摩擦现象之一,与摩擦表面的接触面积和速度无关,与法相载荷成正比,与接触面运动方向相反[2]。
2)黏性摩擦。黏性摩擦来源于摩擦接触表面流体润滑层的黏性行为,与相对速度成比例关系。
3)静摩擦力。静摩擦力是使物体由静止开始运动所需要的力,与速度无关,且大于库伦摩擦力。
4)Stribeck摩擦。Stribeck效应用来描述低速区的摩擦力行为,表现为:在相对速度较低的范围内,摩擦力随着相对速度的增加反而下降。
5)摩擦滞后。摩擦滞后是指摩擦力的改变滞后于相对速度变化的现象,又称为摩擦的记忆效应。摩擦滞后形成一个迟滞环,减速时摩擦力的幅值低于增速时摩擦力的幅值。
1.2 摩擦模型
对重要的摩擦现象建立相应准确的数学模型一直是摩擦学、机械工程等领域的重要研究课题。一个合适的摩擦模型能准确预测摩擦行为、理解摩擦机理,在对有摩擦的机械系统进行设计、控制、研究时占有重要地位。
摩擦模型按摩擦动态可以分为静摩擦模型和动摩擦模型。静摩擦模型将摩擦力描述为接触表面相对于速度的函数,动摩擦模型将摩擦力描述为相对速度和位移的函数。动摩擦模型能更加全面地描述摩擦状态,但由于模型复杂、参数识别非常困难,所以其应用不如静摩擦模型广泛。本文将使用静态摩擦模型。
1)库伦模型。库伦摩擦模型如图1所示。模型描述为

其中:fc为库伦摩擦力;μ为摩擦系数;fn为法向载荷;sgn是方向函数。

图1 库伦摩擦模型
2)库伦+黏性模型。随着流体力学的发展,研究表明液体存在黏性力,从而导致了黏性摩擦模型的出现[3]。库伦+黏性模型如图2所示。模型描述为
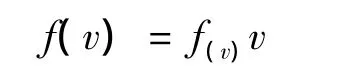
黏性模型一般与库伦模型结合使用,即黏性+库伦摩擦模型:
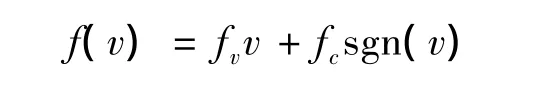

图2 库伦+黏性模型
3)库伦+黏性+静摩擦力模型。实验发现,使物体从零速开始运动所需要的力比保持物体匀速运动所需要的力要大,即静摩擦力要大于库伦摩擦力[4]。库伦+黏性+静摩擦力模型如图3所示。模型描述为
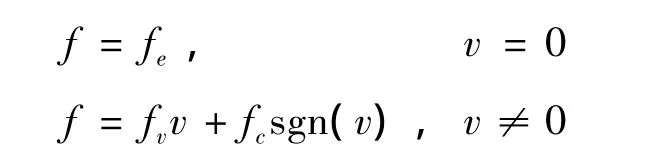

图3 库伦+黏性+静摩擦力模型
图3中fs为最大静摩擦力,在v=0时,摩擦力不是速度的函数。
4)库伦+黏性+静摩擦+Stibeck模型。在之前的经典模型中,摩擦力和速度之间的关系都是线性的,而且静摩擦与动摩擦之间的转化是离散的[5]。对Stribeck的研究表明,实际情况摩擦力并不会出现速度突然下降的情况,而是与速度存在着一定的非线性关系,称为Stribeck效应或者负斜率效应。库伦+黏性+静摩擦+Stibeck模型如图4所示。模型描述为

其中:vs是Stribeck速度;vs和δ都是经验常数。以后在模型中增加了黏性项,变为


图4 库伦+黏性+静摩擦+Stibeck模型
以上是本文所使用的4种摩擦模型[7]。本研究将围绕使用不同的摩擦模型所得到的DCT离合器扭矩曲线与传统方法(摩擦因数假设为定值)的比较展开。
2 DCT模型的建立与分析
2.1 扭矩计算公式
目前,有关DCT研究中离合器扭矩计算时使用的主要公式为[9]
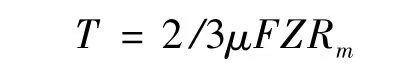
式中:μ为摩擦因数;F为离合器结合压力;Z为摩擦副的数目;Rm为摩擦片的有效摩擦面积。

其中R0、R1分别为摩擦片的内外径。
2.2 结合压力曲线的选取及换挡过程分析
在DCT换挡过程中离合器结合压力的控制是核心技术,本文研究摩擦因数对于输出扭矩的影响,因此使用换挡过程中的压力控制曲线及起步压力控制曲线,如图5所示。DCT换挡与普通单式离合器不同,按照2个离合器状态的不同,整个换挡过程分为5个阶段[10]:低挡—低挡转矩相—惯性相—高挡转矩相—高挡。低挡和高挡阶段都只有1个离合器结合,因此,只有1个摩擦现象发生。在转矩相阶段,2个离合器的主从动盘之间的转速差比较大,适用于不同的摩擦模型。在惯性相阶段,双离合器同时滑磨,摩擦情况最为复杂,应单独分析。综上所述,应把离合器换挡阶段分开讨论,以时间为标准,不同的阶段适用不同的摩擦模型。
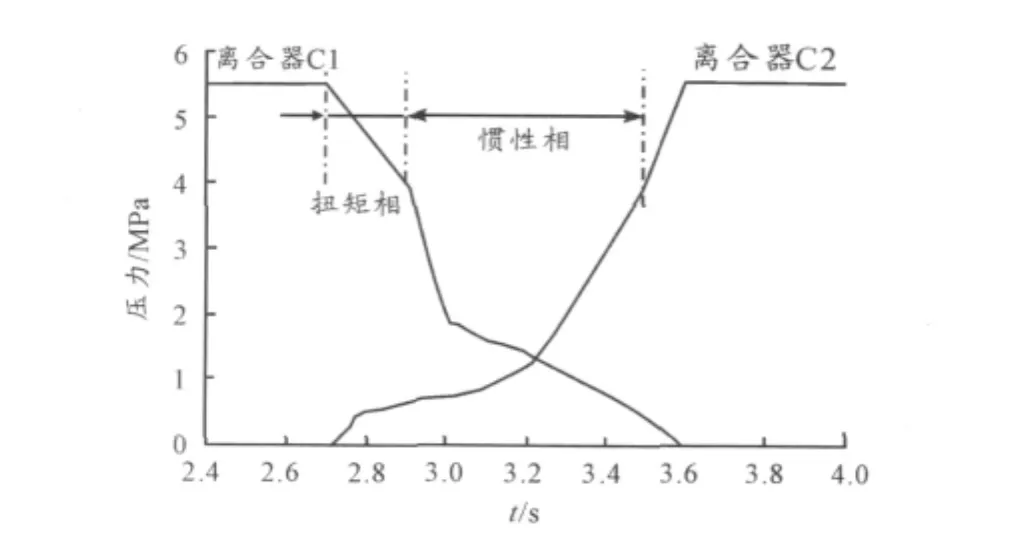
图5 换挡过程中的压力控制曲线及起步压力控制曲线
由图5所得离合器压力变化的分段函数:
1)低挡,C1完全结合,压力不变,C2完全脱开,无压力;
2)低挡转矩相,C1开始放油,C2充油,C1压力由最大开始下降,C2上升,此阶段压力方程为:
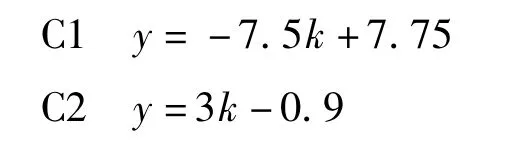
3)惯性相,此阶段两离合器均滑磨

4)高挡转矩相
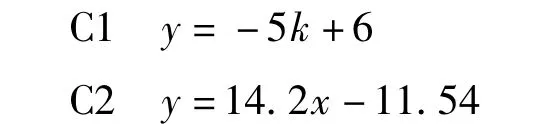
至此,得到换挡各阶段的离合器压力曲线方程。
2.3 摩擦模型分配
根据上节对离合器结合相阶段的分析及不同摩擦模型的适用范围,本文提出了全新的适用于双离合器结合的摩擦模型选用方法,如表1所示。
根据经典转矩公式,建立相应的Matlab模型并带入摩擦因数(摩擦模型)模块,得到新的转矩模型。
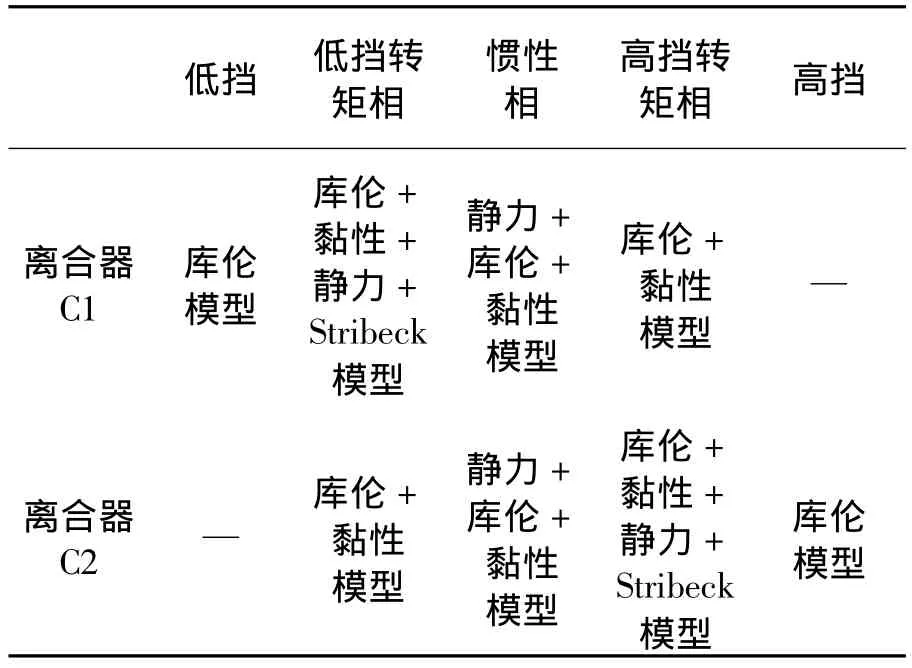
表1 适用于双离合器结合的摩擦模型选用方法
2.4 起步模型
对于起步阶段来说,起步品质主要是冲击度和滑磨功,在起步过程控制方面最大的随机影响因素就是摩擦因数的变化,所以需建立起步模型,研究摩擦模型对起步品质的影响。
本文采用双离合同时结合起步的策略,这种结合方式的优点是滑磨功平均、起步时间短、动力足。模型如图6~7所示。

图6 双离合器起步控制模型
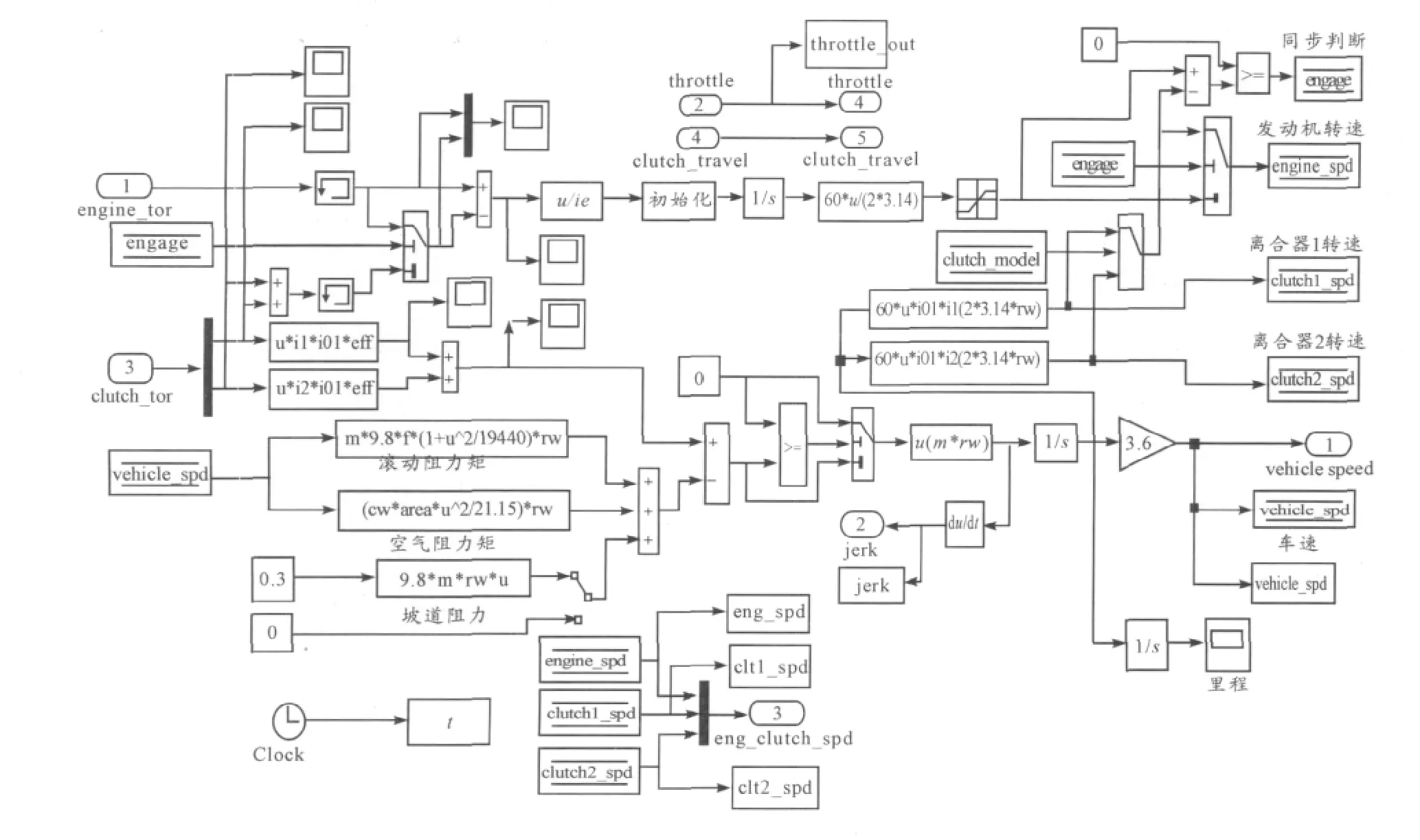
图7 整车传动系统模型
3 结果讨论
3.1 摩擦模型对冲击度的影响
3种情况下整车冲击度的仿真结果如图8~10所示,比较图8与9可知,使用摩擦模型时的冲击度在变化趋势上与使用定摩擦模型时的冲击度没有太大区别,但是在数值范围上有所增加,特别是起步初期及摩擦片将要完全结合时。
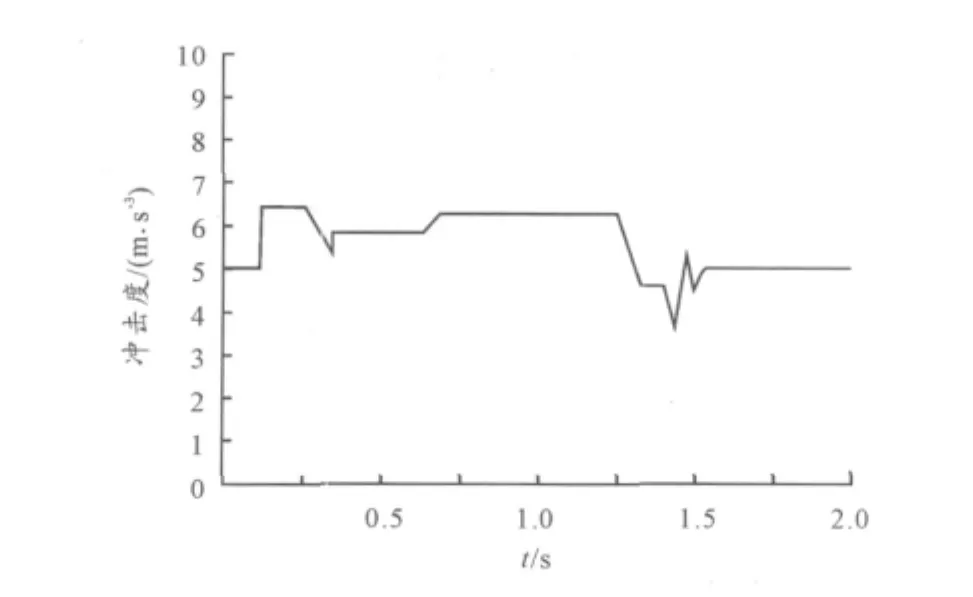
图8 不使用摩擦模型(摩擦因数为定值)的冲击度


在急速起步阶段,使用摩擦模型后,在0~0.5 s的冲击度已达到限定的最大值,而摩擦模型比定值摩擦更能真实地反映出摩擦因数的变化情况,可见,以往研究离合器起步、换挡等控制策略时都将摩擦因数视为定值是有其局限性的。
3.2 摩擦模型对滑磨功的影响
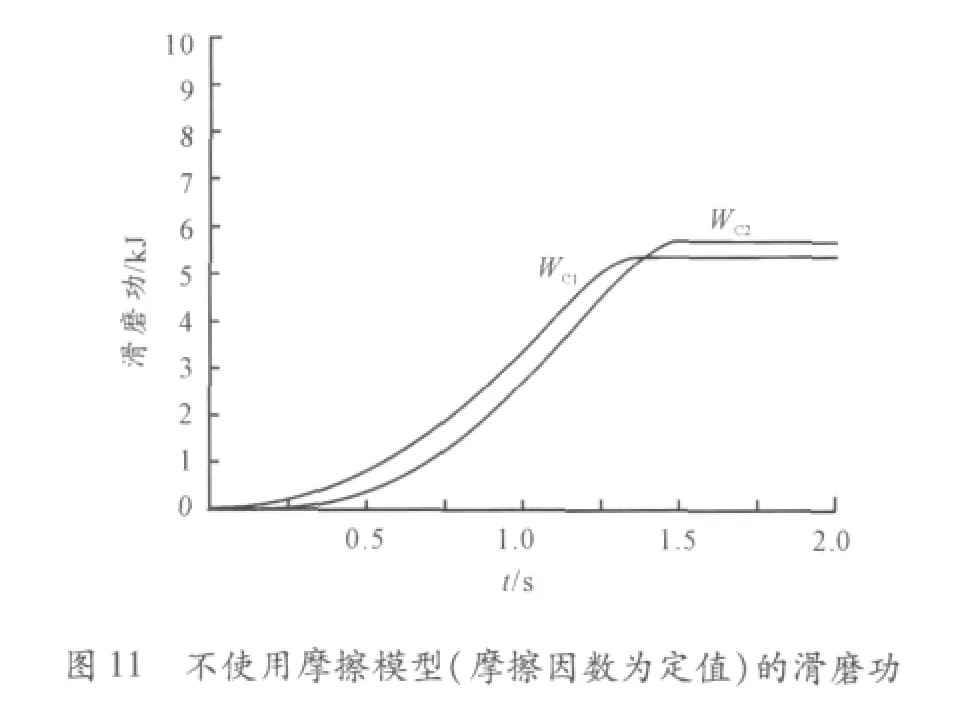
图11、12是在正常起步模式(20%≤油门开度≤60%)下的滑磨功曲线。图11中摩擦因数为定值,而图12中针对离合器C1和C2的相对速度、滑磨状态分别使用了不同的摩擦模型。可见,在使用了合适的摩擦模型的情况下,2个离合器的实际滑磨功与使用定摩擦因数时的仿真结果存在着一定差距。

4 结束语
在研究双离合器换挡、起步的基础上,引入了摩擦模型,补充之前此类研究中通常使用定值摩擦因数的不足,并通过模型得出的冲击度和滑磨功来进行了验证。提出了在换挡阶段按照离合器结合阶段的不同使用相应的摩擦模型的方法,给出摩擦模型使用对照表。当然,速度和位移摩擦模型只是摩擦模型中的一种,温度模型也是影响摩擦因数的一个重要因素,还需深入研究温度在DCT运行过程中产生的影响。
[1]Armstrong B,Dupont P,Canudas de W C.A suivey of models,analysis tools and compensation methods for the control of machines with friction[J].Automatica,1994,30(7):1038-1183.
[2]Armstrong B.Control of Machines with Friction[M].Boston:Kluwer Acadcmic Publishers,1991:24 -26.
[3]Awrejcewicz J,Olejnik P.Analysis of Dynamic Sytems With Various Friction Laws[M].[S.l.]:ASME,2007.
[4]Johannes V I,Green M A,Brockley C A.The role of therate of application of the tangential force in determining the static friction coefficient[J].Wear,1973,24:381-185.
[5]Canuas de Wit C,Olsson H,Lischinsky P,A new model for control of systems with friction[J].IEEE Transactions on Automatic Control,1995,40(3):419 -425.
[6]Berger E J.Friction modeling for dynamic system simulation[J].ASME Appl Mech Rev,2002,55(6):535 -537.
[7]Ibrahim R A.Friction-induced vibration,chatter,squeal,and chaos Part 2:Dynamics and modeling[J].ASME ApplMech Rev,1994,47(7):227 -253.
[8]刘丽兰,刘宏昭,吴子英,等.机械系统中摩擦模型的研究进展[J].力学进展,2008,25(2):201 -213.
[9]双离合器自动变速器系统性能研究[D].重庆:重庆大学,2006.
[10]温诗铸,黄平.摩擦学原理[M].3版.北京:清华大学出版社,2008.

