一种组合飞行器冲突解脱算法

许琴琴

(重庆大学 自动化学院，重庆 400044)

飞行器的冲突解脱是指飞行器即将遭遇障碍物威胁时，综合考虑飞行器机动性能、威胁环境、碰撞概率、飞行时间等约束因素，寻找一条规避障碍物的最优和可行的飞行轨迹。随着我国经济的迅猛发展，以及 IT和电子商务的快速发展，我国的民用航空运输业也进入了高速发展时期，航空运输量增长迅猛。专家预测，未来中国私人飞机的市场规模将会以25%速度递增。在我国空域有限的情况下，理想的冲突探测和解脱得显得更加迫切。

解决飞行冲突的目的是防止航空器在空中相撞，保证飞行安全。国内外对该问题的研究大致分为几种方法:非结构网格法、神经网络法、遗传算法、几何法、矢量法、粒子群法、人工势场法、智能解脱法等。笔者发现上述方法中人工势能法是最直接有效的方法，但是因为势场法的关联参数的最佳调配方案的确定原则不够明晰，以及势场法应用于实际后存在的一些缺点，同时考虑到一些因为舒适和经济等现实条件而要求的角度和速度的限制等，很多学者对该方法进行了改进。笔者考虑引入其他更成熟的思想来弥补势场法的缺点，同时取长补短，从而更好地解决问题。蚁群算法(ACA)是近几年提出的一种新型模拟进化算法。目前，这种方法已成功地解决了旅行商(TSP)问题、Job—shop调度问题、二次指派问题等组合优化问题，显示出蚁群算法解决这类问题的优越性。本文通过研究相关文献，结合我国的空域现状以及有关管制规定，通过对势场法的研究和改进，引入蚁群算法。两者组合的优化算法不仅解决了势场法的很多缺点，同时弥补了蚁群算法收敛性缓慢以及容易出现停滞现象等缺陷，具有更快发现较好解的能力。通过仿真实验，验证了该方法的可行性和有效性。

1 传统势场法存在的问题

通过研究人工势能法，发现势能法简化了周围复杂的环境条件，不用考虑飞行器的状态，不用考虑冲突类型，只要飞行器1落于飞行器2的影响区内，即受到飞行器2势场影响从而偏航解脱。但是在对应用背景进行深入分析后发现，引入势场法后存在如下问题［1－3］:

1)忽略了环境因素(飞行器的机动性能、天气因素、碰撞概率等)等对飞行器的影响。

2)零势能域问题。当飞行器置身于零势能域的环境中时，将不知道如何运动，陷入局部极小点。

3)目标点附近飞行器不可达问题。当飞行器向目标靠近时，距离障碍物越来越近，吸引力减小，斥力增大，飞行器受到排斥而不能达到目标，飞行器在目标前面产生摆动现象，使得飞行器无法到达目的点。

4)可能存在的角度变换过大问题。会引起飞行器内人员的不舒适感以及其他可能的安全隐患。

5)飞行器安全间隔没有纳入考虑。

6)多架飞行器同航迹冲突问题。此时势场法产生的合力方向仍然是在原来的方向上，并未做任何改变，甚至要求飞行器向后退，而这些都是不合情理的。

7)飞行器速度和冲突类型的影响。

空域内各个飞行器速度不同，如果不加以区别，也不能很好地进行解脱。

2 引入蚁群算法的优缺点

蚁群算法是20世纪90年代发展起来一种模仿蚂蚁群体行为的新的智能优化算法［4－6］。该算法引入正反馈并行机制，具有较强的鲁棒性、优良的分布式计算机制、易于与其他方法结合等优点。将蚁群算法应用于空中交通冲突解脱的优点是，引入“状态参数”表示天气、交通复杂度等诸多不确定因素对空中交通的影响，引入代价函数描述解脱航路的性能指标，根据满足“合理路径”的条件规划出包含不确定因素影响的“虚拟路径”，并比较计算出的各种解脱路径的“虚拟路径”长度，从诸多“合理路径”中优选出最佳路径。

蚁群算法是一种确定性状态空间搜索算法，计算开销大、收敛速度慢一直是学者比较关注的问题［8－10］。蚁群算法受起止点位置和障碍分布的影响，环境复杂时蚂蚁容易陷入不可行点，甚至出现路径迂回和死锁。蚁群算法容易出现停滞现象，即搜索进行到一定程度后，所有蚂蚁搜索到的解完全一致，不能对空间进行进一步搜索，不利于发现更好的解。

3 组合优化方案设计

鉴于传统势场法和蚁群算法的优缺点，笔者考虑将两者结合进行解脱航迹的优化。

在所定义的飞行器系统中，有m个飞行器，所研究第i个飞行器任意时刻位置矢量为Xi(xi，yi，zi)(i∈{1，2，3，…，m})，目标点为 Xo(xo，yo，zo)(o∈{1，2，3，…，m})，计划航线为从起点到目标点的直线。其余m－1个飞行器都为第i个飞行器的潜在冲突障碍。设定第j个障碍飞行器位置矢量用 Xj(xj，yj，zj)(j∈{1，2，3，…，m －1}且 j≠i)表示，所研究飞行器跟目标点的距离为dio，所研究飞行器与潜在冲突飞行器的距离为dij，飞行器保护区半径为rpro，影响区半径为reffect。

划定飞行器避障空域范围为R×R，栅格化该范围。在第i个飞行器的位置点放置n个蚂蚁，每只蚂蚁使用一定的状态转移规则从一个状态转移到另一个状态，直到最终达到目标点，完成一条候选航路。

状态转移规则类同于基本蚁群算法。蚂蚁在运动过程中，根据各条边上的信息量以及路径的启发信息来计算状态转移概率。表示在t时刻蚂蚁k由元素i(导航点)转移到元素j(导航点)的状态转移概率。

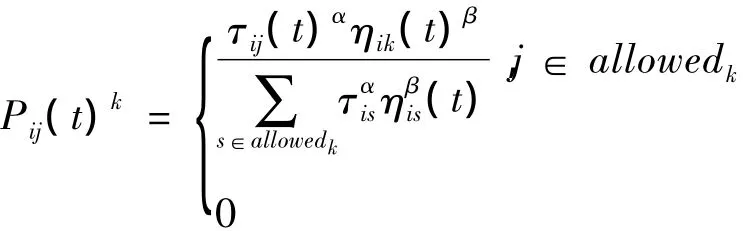
式中:allowedk表示蚂蚁下一步允许选择的导航点;α为信息启发因子，表示轨迹的相对重要性，反映了蚂蚁在运动过程中所积累的信息在蚂蚁运动过程中所起的作用，其值越大，蚂蚁越倾向于选择其他蚂蚁经过的路径，蚂蚁间的协作性越强;β为期望启发因子，表示能见度的相对重要性，反映了蚂蚁在运动过程中启发信息在蚂蚁选择路径中的重视程度。

ηij(t)为启发函数，考虑人们对合理航路可能考虑的几个因素:路径最短，代价最小，时间最小，跟计划航线不能偏航太远等。其表达式为

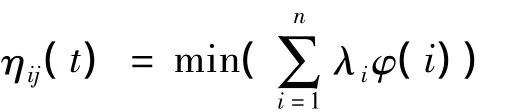
其中:φ(i)与需要考虑的几种因素相对应;λi是上述几个因素权衡值，可以取。希望解决与约束因素问题同时出现的路径最优问题，但是当只出现其中1个或几个约束时，算法仍然成立。例如当考虑路径最短时 λ1=1，λ2=λ3=λ4=0，，此时启发函数与传统蚁群算法相同，式中dij表示相邻2个导航点之间的距离。对蚂蚁k而言，dij越小，则 ηij(t)越大(t)也越大，该启发函数表示蚂蚁从导航点i到导航点j的期望程度。

一旦所有蚂蚁完成了各自候选航路的选择过程，必须对各边上的信息素做一次全面的更新，其更新规则为

蚂蚁 k(k=1，2，3，…，m)在运动过程中根据各条路径上的信息量决定其转移方向，信息素更新规则:

式中:Wk表示蚂蚁k选择的航路的广义代价;We代表当前最小的航路代价。信息素更新的目的是分配更多的信息素到具有更小威胁代价的航路边上。

最后根据航路性能指标计算最短航路:

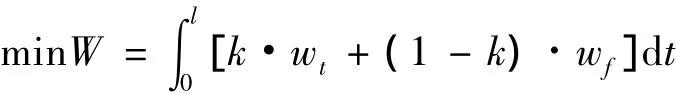
其中:l表示航路长度;W表示广义代价函数;wt表示航路威胁代价;wf表示航路油耗代价;k表示倾向性选择。

传统蚁群算法在栅格化的整个划定空域寻找最优路径，对于大规模问题求解具有收敛缓慢的缺点，因此在状态转移时，考虑引入势场法，根据势场法计算的合力方向缩小蚁群算法的可选空域，从而加快收敛时间。

将目标视为点电荷，则飞行器Xi与目标位置Xo之间的引力场为

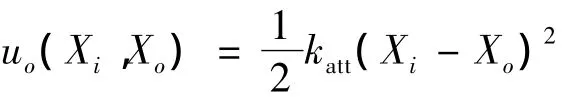
其中katt为引力增益系数。

定义引力为引力场的负梯度

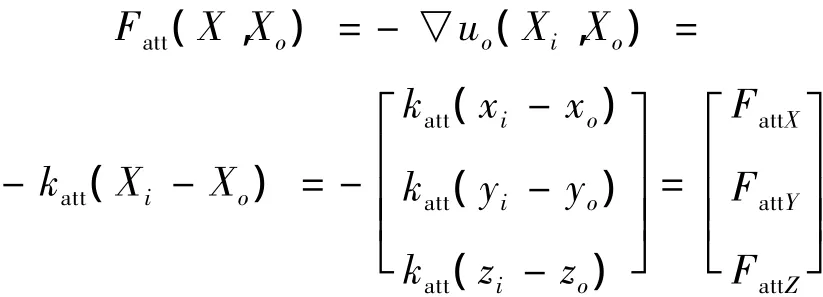
其他的相关飞行器视为障碍物，为避免飞行器Xi和其他飞行器Xj之间的冲突，将其他飞行器也视为点电荷，由其他飞行器中飞行器Xj形成的斥力势场函数为

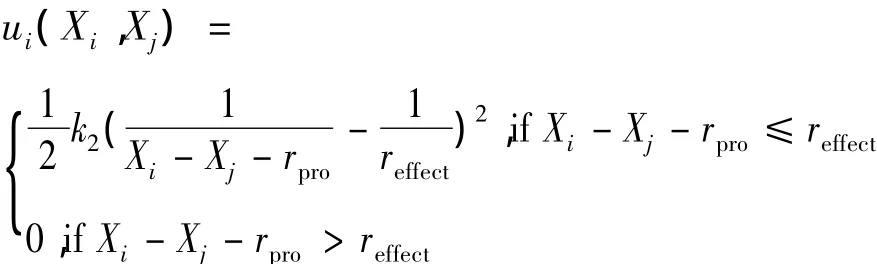
其中:krep为斥力增益系数，并且分布于一定范围;(Xi－ Xj)为飞行器 Xi到 Xj距离;rpro，reffect分别为保护区和影响区设定值。由公式可以看出，2架飞行器距离越近，特别是当Xi靠近Xj保护区边缘时，势场达到无限大，阻止了一个飞行器进入其他飞行器保护区的可能性。

定义斥力为斥力场的负梯度:

设合力方向与 x，y，z轴所成角度为 α、β、γ，则有

此即得到飞行器在势场作用下到下一位置点的移动方向。应用组合优化算法的流程如图1所示。

4 仿真实现

为验证该方法的有效性，本文采用2机冲突解脱任务来测试算法的性能，并与传统蚁群算法以及势场法相比较。为了比较的公平性，本文算法和蚁群算法以及势场法采用相同的群体规模(4架飞行器，60只蚂蚁)，而且在每组测试中均迭代相同的次数。同时为了简化冲突环境，考虑飞行器的计划航线为直线。在每个测试实例中，以图形化的方式给出了这3种方法生成的最优路径以及所需时间的比较，并对解的分布性能以及散布范围等作了比较。

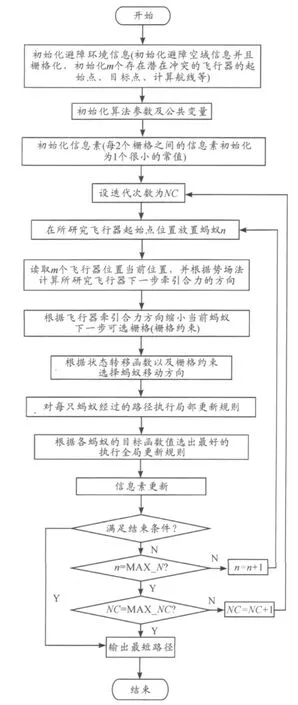
图1 组合优化算法流程

2架飞行器的起始点位置为(0，0)，(0，100)，目标分别为(100，100)，(100，0)。2架飞行器的潜在冲突点为(50，50)。考虑到飞行器的保护区范围为20，为了有充裕的时间选择最好的路径以最短的时间避过撞机风险，那么2架飞行器在进入保护区之前就必须开始避障算法，因此假定2架飞行器从起始点开始引入避障算法。实验仿真后的结果如图2所示。

图2 仿真结果

图2(a)、(b)表示其中一架飞行器按照计划路线飞行，另一架飞行器按照解脱方案进行解脱后的路线，图2(c)表示2架飞行器同时执行解脱后的路线。实验结果比较如表1所示。

从图2可以看出，采用人工势能法与蚁群算法相结合，规划出的轨迹能够有效地避免冲突，使飞行器安全有效地执行飞行任务。

表1 算法性能比较

5 结束语

势能法是比较成熟的路径规划算法，特别在机器人领域。近些年相关研究人员考虑将其引入到飞行器冲突解脱中来。采用势能法进行飞行器冲突解脱需要的环境信息较少，目的性比较明确，计算量少，易于实现实时控制，但是由于算法本身的缺陷，在引入实际应用的过程中出现了很多缺点，本文在前人研究的基础上，将蚁群算法与势场法结合，仿真表明，二者结合具有以下特点:

1)利用势场法规划的路径动态约束蚁群寻址的有效范围，可以帮助蚁群算法更好更快地收敛，弥补了传统蚁群算法首次搜索路径范围过大而导致的计算量大的缺陷。

2)最优路径的选取是众多蚂蚁的合作被搜索到的，并成为大多蚂蚁所选择的路线，这一过程具有协同性。

3)可以将飞行器飞行环境中很多不确定因素比如天气因素、机动性能等体现在启发因子中，更贴近实际情况。

［1］Michael A，Goodrich.Potential Fields Tutorial［Z］.［S.l.］:［s.n.］，2003.

［2］郭茜.改进人工势场法在解决飞行冲突问题中的应用［J］.交通与计算机，2008(5):21 －25.

［3］黄兴华.基于改进人工势场法的移动机器人路径规划［J］.计算机应用，2010(6):45 －48.

［4］杨剑峰.蚁群算法及其应用研究［D］.杭州:浙江大学，2007.

［5］邓蕾蕾;张献.改进的蚁群算法在灌区渠系优化配水中的应用研究［J］.安徽农业科学，2011(31):19330－19332，19360.

［6］崔建国，郑新起，邱楠，等.基于EMD包络谱的飞行器健康诊断［J］.压电与声光，2009(6):807 －809.

［7］陶红艳.无线传感器网络动态分簇路由BWAS的算法研究［J］.压电与声光，2011(1):155－160.

［8］李明.蚁群算法在土地利用结构优化模型中的应用［J］.安徽农业科学，2011(14):8461 －8462.

［9］侯文英，秦驰越.基于蚁群算法鲜活农产品配送路径优化研究［J］.安徽农业科学，2009(1):109－110.

［10］王越，黄丽丰.一种基于无相交搜索策略的蚁群算法［J］.重庆理工大学学报:自然科学版，2011(4):65－69.