带线性红利的非齐次复合Poisson风险模型
韩孟云
(河海大学理学院,南京 200098)
风险理论是当前精算学界和数学界研究的热门课题。自古典的风险模型被提出后,许多研究人员对此进行了推广,以使其更符合保险公司的实际经营情况。但很多研究只考虑了索赔到达的复合齐次泊松过程,并没有考虑资金的时间价值以及投资收益等其他资金活动的影响,这具有一定的局限性。
近几年来,大量文献对经典风险模型进行了研究,并取得了有关破产概率方面的结果[1-3]。经典风险模型是假设保险公司按照单位时间常数速率(每张保单的保费为常数c),但任何风险事业都是在随机环境中进行的,因此,保费收取过程应是一随机过程。文献[4-6]利用Poisson过程对此进行了研究,文献[7]又把线性红利因素引入了风险模型。本文在文献[7]的基础上把索赔过程推广为非齐次复合泊松风险模型,使得模型更贴近实际。
1 模型的建立
定义1 设 u≥0,给定概率空间(Ω,F,P),t≥0。令

对模型(1)作如下假设:
1){Xi,i≥1},{Yj,j≥1}是均值分别为 λ,μ 的非负独立同分布随机变量序列,其分布函数分别为F(x),H(x)。
2){M(t),t≥0},{N(t),t≥0}分别是参数为 A(t)、B(t)的非齐次泊松过程。
3){Xi,i≥1},{Yj,j≥1},{M(t),t≥0},{N(t),t≥0}相互独立。
定义2 设定一个线性红利界限z=b+qt,其中b为初值(u≤b),q为递增速率(0<q< λ2μ2),只要盈余在红利界限以下,便不发放红利,若盈余在红利界限以上,每单位时间发放λA(t)-q的红利,直至下一次索赔发生,于是有如下关系式:

定义3 保险公司最终破产概率ψ(a,b)=P{T<∞,R(0)=u};T=min{t:t≥0且R(t)<0}表示破产概率。
定义4 令

2 主要结果
由文献[2]中式(3.(6.3))可知,只要 ν(z,,t)满足式(4),它便为一鞅。

定理1 当dR(t)=dS1(t)-dS2(t)时,满足式(5)的 ν(z,t)能使 ν(R(t),t)为一鞅。
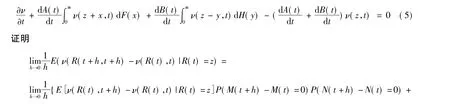

由此可知ν(R(t),t)只要满足式(5)它便满足式(4),就为一鞅。所以在带线性红利的非齐次Poisson风险模型中,要找 ν(z,t)使得 ν(R(t),t)为一鞅,ν(z,t)只要满足:

这样,转而寻找这样一个函数,使得方程(6)所有的z和t皆成立,并满足
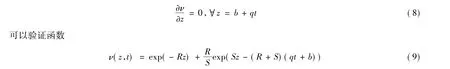
即为满足式(6)和(8)的ν(z,t),其中R是方程
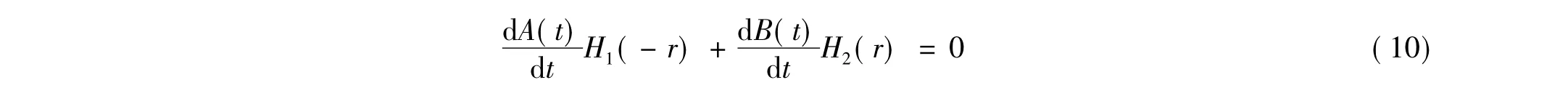
的非平凡正解,S为方程
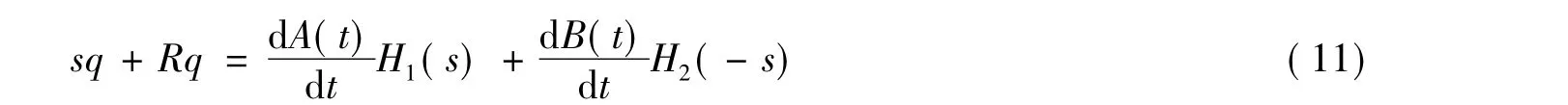
的唯一正解。
3 最终破产概率
定理2 在带线性红利的非齐次复合Poisson过程下的最终破产概率为

证明 假设T为破产时刻,对固定的时刻t,可证得TΛt是有界停时,利用有界停时定理知,由式(9)所确定的鞅{ν(R(t),t)}有

将ν代入式(16)即得到式(12),至此得出了带线性红利的非齐次复合Poisson风险模型的破产概率上界。
[1]GRANDEL L J.Aspects of risk theory[M].New York:Spring-Verlag,1991.
[2]GERBER H U.数学风险引论[M].成世学,严颖,译.北京:世界图书出版发行公司,1997.
[3]成世学.破产论研究综述[J].数学进展,2002,31(5):403 -422.
[4]方世祖,罗建华.双复合Poisson风险模型[J].纯粹数学与应用数学,2006,22(2):271-278.
[5]杨善朝,马翀,谭激扬.保费随机收取的风险模型[J].经济数学,2004,21(1):1-5.
[6]钟朝艳,何树红,黑韶敏.古典模型的一个推广[J].云南民族大学学报:自然科学版,2006,15(1):25-27.
[7]江五元,武坤.带线性红利的双复合过程风险模型的破产概率[J].经济数学,2005,22(3):276-278.
[8]肖碧海.几类非齐次复合泊松风险模型的研究[D].长沙:中南大学,2006.
[9]赵金娥,王贵红,龙瑶,等.线性红利下带干扰的复合Poisson风险模型[J].重庆理工大学学报:自然科学版,2010(3):115-120.

