S-SMART最大熵法及在小样本中的应用

屈云利，朱永忠

(河海大学理学院，南京 210098)

目前，用于解决小样本问题的方法之一就是Bayes方法。利用Bayes方法的关键是如何有效地利用先验信息来合理地确定先验分布。许多学者对此进行了研究，如:Raiffa和Schlaifer［1］提出了利用共轭先验分布来确定先验分布;Jeffreys［2］研究提出了Jeffreys原则;Box和Tiao［3］对无信息先验分布作了详细的研究;20世纪50年代以 Robbins［4］为代表提出用经验 Bayes方法(EB)确定先验分布。

随着信息论的产生，Jaynes等［5］利用信息论中熵的概念提出用最大熵法来确定先验分布，在获得少量的统计样本值时就可以获得它的概率密度函数。这种方法充分利用了样本中给定的信息，可以做到准确地确定概率密度分布以及相关的各个参数。随着计算机的发展，对于小样本问题，常利用一些非参数的统计方法(如Bootstrap［6］方法和S-SMART(sample-smoothing amplification technique)［7］方法确定先验分布，并取得了较好的应用效果。一些参数方法都是针对大样本的［8］。研究表明S-SMART方法比Bootstrap方法更稳健，尤其在小样本的情形下比Bootstrap方法更精确、效果更好［7］。最大熵法也不需要对试验数据进行假设就能确定先验分布，它是一种较好地处理不完全先验信息和尽量避免主观因素的方法［9］。在先验样本数据较多时，可替代经典统计学中通过直方图确定概率分布的方法，且给出的是连续分布函数，便于利用Bayes公式进行计算。由此本文结合S-SMART方法和最大熵法的特点来进行相关研究，提出应用S-SMART最大熵法可以直接由试验数据得到未知参数的连续概率密度函数，且几乎不需要人为假设，完全依赖样本信息，客观地得出该样本的近似分布密度函数。

1 S-SMART最大熵法理论

S-SMART最大熵法的基本思想是:通过 SSMART方法将小样本问题转化成大样本问题后，再利用最大熵法求出其概率密度函数，从而解决小样本情况下Bayes统计方法中的先验分布确定问题。

1.1 最大熵方法的理论

信息论中熵用来表示不确定性的量度。信息熵的定义是

其中:Pi为随机变量取 xi时的概率;SUM为累加和。

当x为连续型时，熵的定义可以写成

其中f(x)为随机变量分布的概率密度函数。

最大熵的实质就是在已知部分知识的前提下，关于未知分布最合理的推断，就是符合已知知识最不确定或最随机的推断，即信息量最大的概率密度函数就是最佳(偏差最小)的概率密度函数。

设θ是连续型随机变量，p(θ)是 θ的概率密度。

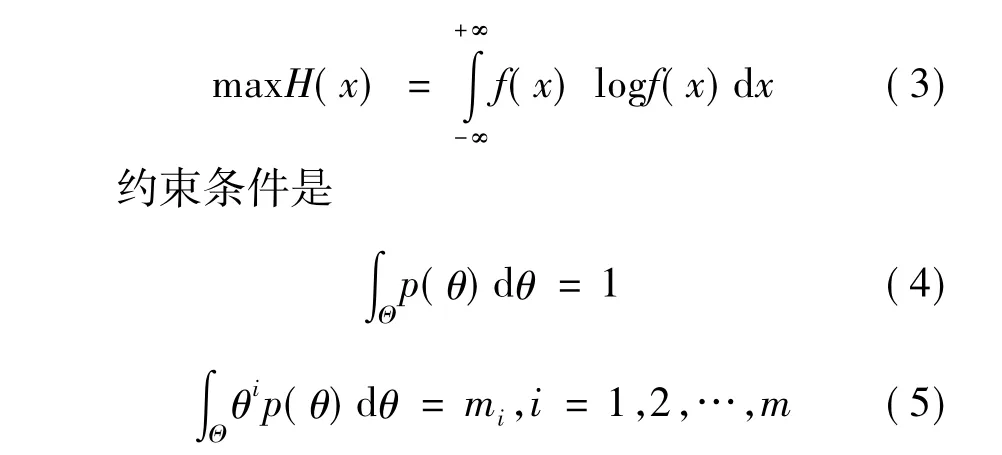
其中mi为随机变量θ的各阶原点矩。

通过构造拉格朗日方程，使熵达到最大值，通过计算可得随机变量θ的概率密度函数

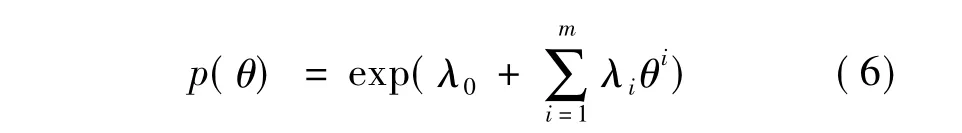
其中 λ0，λ1，…λm为待定系数［10］，可由式(4)、(5)求解。

1.2 S-SMART最大熵法的方法实现

考虑如下问题:设随机样本 X=(x1，x2，…，xn)是来自未知的总体分布F。当n很大时(即大样本数据)，可以采用经验分布函数法、直方图法来近似求得总体的概率分布;但当n不大时(即小样本数据)，上述方法的误差会比较大。现以小样本问题为例来说明S-SMART最大熵法的实现步骤。

1)对已知的样本观测值进行再抽样得到SSMART样本。具体的抽样过程是:首先将原始样本的2.5% ～97.5%的百分位点概率等分为k份(k为样本的放大倍数)，然后计算相应的分位点和原始样本的标准差，之后以服从上述步骤中获得的百分位点为均值，以原始样本的标准差为标准差的正态分布来模拟产生k组S-SMART子样，最后将这 k组S-SMART子样结合起来获得 SSMART样本。

2) 记所要考察的未知参数θ^=R(X，F)，θ^可以是总体的均值、方差或分布密度函数等分布特征。

3)借助计算机，利用Monte-Carlo方法对步骤1)和步骤2)进行N次模拟，得到估计参数的序列

其中Θ为参数空间。结合以上步骤可获得p(θ)的表达式，从而可对随机变量进行相关的假设检验。

2 仿真模拟及结论

根据以上步骤并不能得到p(θ)的解析表达式，只能利用数值方法进行求解。一般情况下，m取到3或4即可满足较高的精度和工程需要，视具体情况而定。本文以m=4为例来进行仿真模拟试验。

1)以不同的放大倍数和不同的分布为例，设随机样本分别来自标准正态分布N(0，1)和参数为10的指数分布，每个含有n个随机数，n取20，利用S-SMART方法进行10次和50次的再抽样，应用Matlab［11］中统计工具箱计算各自的各阶矩。

图1～4分别表示运用S-SMART最大熵法放大10倍、50倍的模拟结果与理论的标准正态分布和参数为10的指数分布的比较，其中‘o’是样本点。由图1～4可以看出，在小样本情形下，利用S-SMART最大熵法确定的先验分布与各理论分布相近，若直接将小样本进行拟合则与实际结果相差很大。由此可见S-SMART最大熵法是可行、有效的。这表明S-SMART最大熵法根据小样本数据求取未知参数的先验分布不需要对分布作假设即可得到连续的概率密度函数，便于进行理论分析。该方法即可有效地扩充样本数据，同时也能充分利用样本信息，尽量避免主观因素的影响，因此得到的先验分布也更能令人信服。

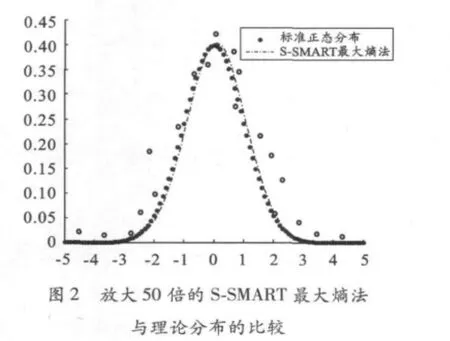
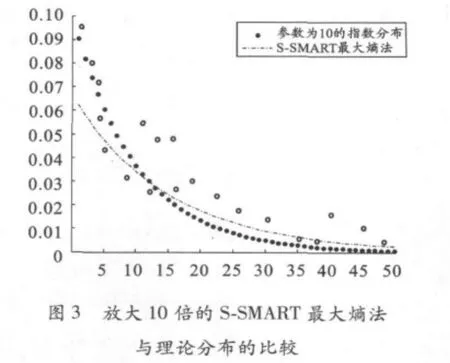
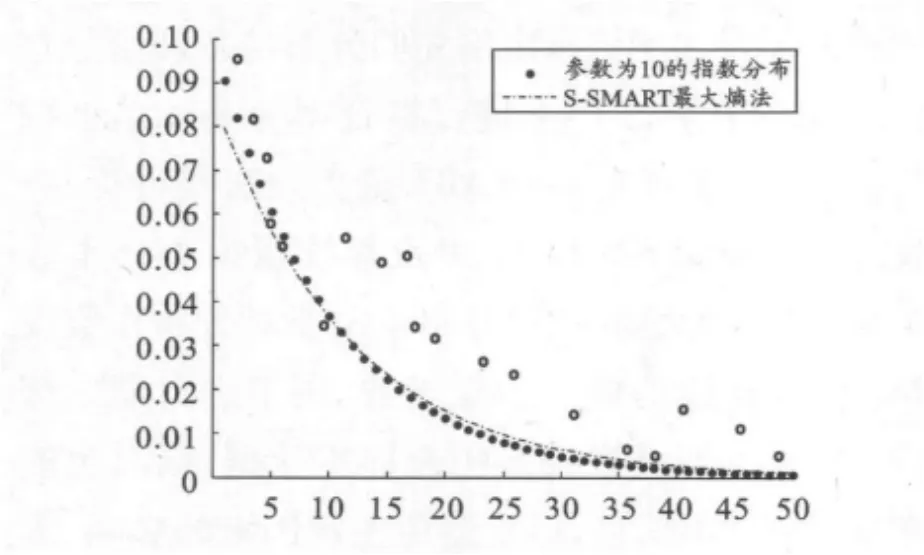
图4 放大50倍的S-SMART最大熵法与理论分布的比较

［1］Raiffa H，Schlaifer R.Applied Statistical Decision Theory［M］.Boston:Harvard University Press，1961.

［2］JeffreysH.Theory of Probability［M］.Oxford:Oxford University Press，1961.

［3］Box C，Tiao G C.BayesianInferenceinStatisticalAnalysis［M］.USA:Addision-Wrsley，1973.

［4］Robbines H.The Empirical Bayes Approach to Statistical Decision Problem［J］.Ann.Math.Stat.，1964，35:1 －20.

［5］Jaynes E T.Information Theory and Statistical Mechanics［J］.Phys.Rev，1957，108(2):171 －190.

［6］Efron B.Bootstrap Method:Another Look At The Jackknife［J］.Ann Statist，1979，1:1 － 26.

［7］Haiyan Bai.A New Resampling Method to Improve Quality of Research with Small Samples［D］.Cincinnati:University of Cincinnati，2006.

［8］余嘉元.基于神经网络集成的IRT参数估计［J］.江南大学学报，2009(5):505－508.

［9］康文兴，谷小松，黄希利.自助最大熵法确定先验分布及其在导弹命中概率估计中的应用［J］.装备指挥技术学院学报，2007(3):109－113.

［10］张焕珍.基于蒙特卡罗和最大熵法的水泵测试不确定度研究［D］.沈阳:沈阳工业大学，2010.

［11］苏金明，张莲花，刘波，等.MATLAB工具箱应用［M］.北京:电子工业出版社，2004.