隐私保护数据挖掘算法MASK的改进

王 茜，张鲲鹏

(重庆大学计算机学院，重庆 400044)

近年来随着数据挖掘技术的发展，数据隐私保护逐渐引起人们普遍的关注［1－2］。Rizvi S J等［3］于 2002年提出了基于随机扰动的 MASK(mining associations with secrecy konstraints)算法。该方法很好地解决了在保持高度隐私的同时获得较为准确的挖掘结果的问题，但该算法运行的时间效率较低。武振华等［4］在此基础上改进了MASK算法。称之为XMASK算法［4］，该算法利用分治策略简化求解逆矩阵的过程，从而提高了算法的运行效率。本文提出一种基于XMASK算法的改进算法。复杂度分析和实验结果都表明本文提出的算法在保证隐私度和准确度不变的同时明显提高了运行的时间效率。

1 MASK算法和XMASK算法

MASK算法由Rizvi提出。假定数据集为超市购物数据篮，所挖掘的数据集可以看作由0和1组成的二维稀疏布尔矩阵，1表示购买某件商品，0表示没有购买。为了保护输入数据集的隐私性，MASK算法采用概率歪曲的方法对原始数据集进行扰乱操作。一个0－1数据库元组可以看成一个随机向量X={Xi}，Xi=0或者1。对Xi进行歪曲操作得到 Yi=XiXOR，其中是 ri的补，ri是满足贝努利分布的随机变量，分布律p(ri=1)=p，p(ri=0)=1－p。由异或计算的特点可知随机向量X经过歪曲操作后，第i个分量Xi保持原值的概率为p，取其相反值的概率为1－p。

MASK算法所挖掘的数据集是真实数据集经过概率变换形成的，所以需要重构项集的真实支持度。设真实数据集对应的矩阵为T，T经过歪曲变换后得到的矩阵为D，歪曲概率为p。T的第i列中1的个数记为，0的个数为，D中第 i列中1的个数为，0的个数为。由前面的概率歪曲过程可知:

所以

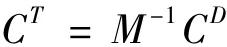
n－项集的真实度估算方法跟单项集类似，方法如下:

由于MASK算法重构数据项真实支持度的指数级复杂度，使得该算法运行的时间效率较差。基于MASK算法，大量改进的算法被提出。武振华等于2008年提出一种基于MASK的改进算法XMASK。

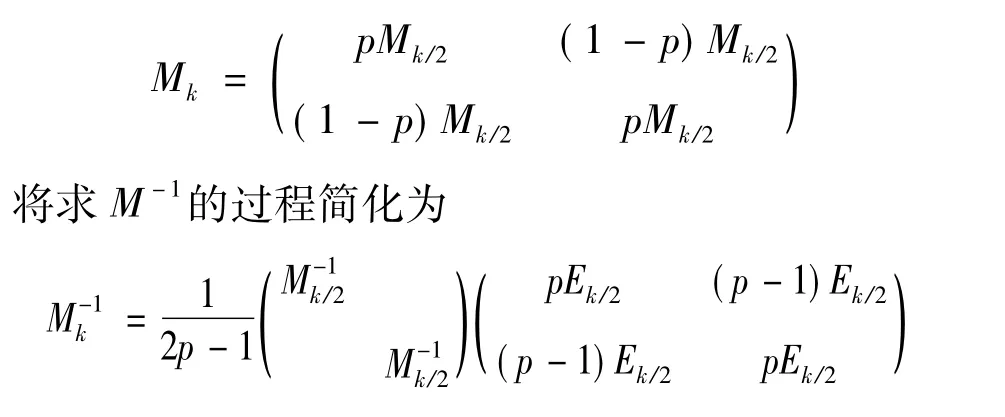
XMASK改进算法在求解M－1的过程中，利用低阶与高阶M中所存在的递归关系从而使重构数据项支持度的时间复杂度由原来的O(8n)降低为O(2n)，使得算法在时间性能上提高了2个数量级，大大提升了算法的执行效率，是一种非常有效的改进。

2 新的优化方法

XMASK改进算法在求解概率矩阵方面很有效，但是当求解概率矩阵的时间复杂度降低到一定的数量级后，在重构数据项真实支持度时对歪曲矩阵中各个组合的计数过程的指数级时间复杂度仍然制约着算法的执行效率。

2.1 新算法的描述

MASK算法的实现基于经典Apriori算法，先产生频繁1－项集，再产生频繁k－项集，最后生成强关联规则。与经典Apriori算法不同的是项集的计数问题。MASK算法需要从歪曲后的数据集估算真实数据集中项集的支持度，例如对于2－项集，原始项集11歪曲后会变为00，01，10，11中的一种，所以要得到真实2－项集的支持度需要考虑4种变化情况。而对于k－项集，就需要考虑2k种变化情况，由此可见MASK算法在对扭曲矩阵各个组合进行计数的开销也是十分巨大的。

MASK算法所挖掘的数据集是二维稀疏布尔矩阵，而在对歪曲项集的实际计数过程中不难发现，由于布尔数据集的特性，各数据集的计数并不是毫无关联的，例如在二次频繁集{A、B}的计算中，只需查询出A、B取值全为1，即11的个数，其余取值组合则可以表示为

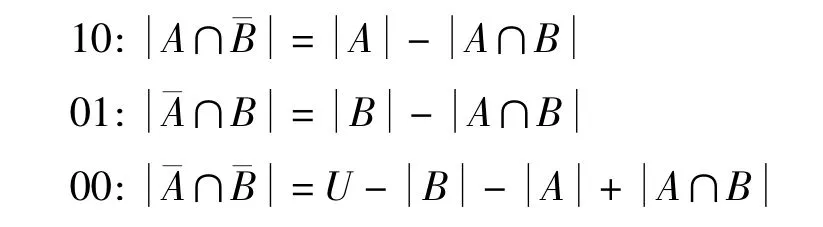
其中A、B的取值可以在之前的1－项集挖掘中得到，而在 n次频繁集的计算中，可将此规则归纳为［5］:

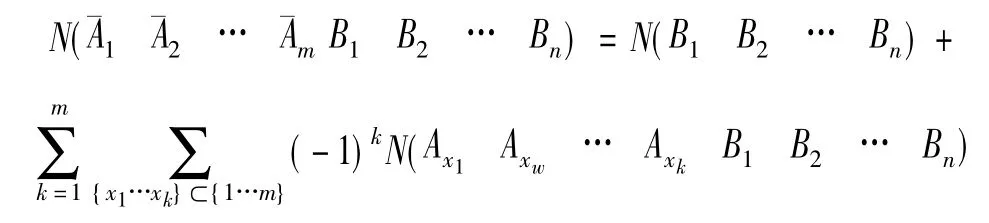
利用此公式，对于任意K次候选频繁项集，只需要在歪曲数据集合中查询一次取值全为1的项集个数，其他组合的个数可通过利用之前在项集挖掘中得到的频繁项集取值全为1的计数，并结合此公式求得。在挖掘过程中，通过哈希链表来存储各取值全为1的项集的个数以供后续的挖掘使用。这样就可以显著减小算法在歪曲数据集中计数过程的开销。

2.2 完整的改进算法的实现

改进的算法在XMASK算法的基础上，增加函数cal(A，p)用于计算项集A在歪曲矩阵中的计数，哈希链表hashtab在存储频繁项集在歪曲矩阵中取值均为1的个数。下面是改进算法的实现过程:

3 实验及结果分析

为了验证改进算法的性能，通过实验将原MASK算法与XMASK算法进行比对。本实验的硬件环境为联想B3电脑，配置为Pentium®Dual-Core CPU E63002.80GHz处理器和2G内存，操作系统为Windows XP，开发工具为Visual C++6.0。

实验采用的数据集由IBM Almaden generator生成。数据集的参数设定为T12I5D100KN0.02，表示数据集中的数据的平均长度为12，频繁项集的平均长度为5，数据集总共有100000个数据，属性的总个数为20。

在实验中，数据库以参数p=0.8进行扭曲，最小支持度min_sup为10%，运行结果见图1。

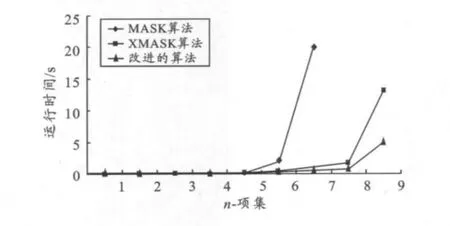
图1 3种算法的比较

由实验结果可知:当n≥5的时候，3种算法的运行时间差别不大;当n=6的时候，XMASK算法与改进后的算法的执行效率比原MASK算法提升了3到4倍;当n≥7时，原MASK算法的执行效率急剧退化，而XMASK算法与改进算法仍然保持了良好的执行效果;当n的阶数提升至8和9的时候，改进算法的运行时间仅为0.768 s和5.143 s，相对于XMASK 算法的1.563 s和13.259 s，执行时间效率提升了2到3倍。这样的实验结果表明，本文改进后的算法在时间性能上明显优于原MASK算法和XMASK算法。

4 结束语

本文针对MASK算法执行效率低下的问题，基于XMASK算法提出了新的改进算法，利用布尔数据集的特性，通过已知项求解未知项的方法降低了对扭曲数据集的访问次数，使算法在时间效率上得到显著的提高。最后，通过实验证明了改进后的MASK算法具有更高的时间效率。

［1］Verykios V S，Bertino E，Fovino I N，et al.State-of-the-Art in privacy preserving datamining［J］.SIGMOD Record，2004，33(1):50 －57.

［2］陈晓明，李军怀，彭军，等.隐私保护数据挖掘算法综述［J］.计算机科学，2007，34(6):183 －186.

［3］Rizvi S，Haritsa J R.Maintaining Data Privacy in Association Rule Mining［C］//Proc.of 28thInt.Conf.On Very Large Databases，USA:［s.n.］，2002.

［4］武振华，刘山，崔健国.基于分治策略的MASK算法的改进［J］.微计算机信息，2009(36):78－80.

［5］Agrawal R，Imielinski T，Swami A.Mining association rules between sets of items in large databases［C］//Proc.Of ACM SIGMOD Intl.Conf.On management of data.USA:［s.n.］，1993.

［6］Agrawal S，Krishnan V，Haritsa J R.On addressing efficiency concerns in privacy-preserving minning［M］//Lee Y J，Li J Z，Whang K Y，et al.Proc.of the 9thIntl.Conf.On Database Systems for Advanced Applications.LNCX 2973.Jeju Island:Springer-Verlag，2004:113－124.

［7］黄毅群，卢正鼎，胡和平，等.分布式环境下保持隐私的关联规则挖掘算法［J］.计算机工程，2006，32(13):12－14.

［8］Alexey Pryakhin，Matthias Schubert，Arthur Zimek，et al.Future trends in data mining［J］.Data Min Knowl Disc，2007，15:87 －97.