随机反演在陆丰13-1油田储层预测中的应用
刘 丹,徐 伟
(1.中国地质大学 地球物理与信息技术学院,北京 100083;2.中国地质大学 能源学院,北京 100083)
随机反演在陆丰13-1油田储层预测中的应用
刘 丹1,徐 伟2
(1.中国地质大学 地球物理与信息技术学院,北京 100083;2.中国地质大学 能源学院,北京 100083)
这里以陆丰13-1油田为例,研究发现井上波阻抗曲线并不能有效区分砂岩储层和泥岩非储层,故对孔隙度数据体进行了反演。首先对井上孔隙度曲线进行直方图统计分析,变差函数分析及孔隙度和波阻抗的相关性分析,然后用高斯模拟加模拟退火的随机反演方法对研究区进行了孔隙度体的反演。经反演发现,较其它反演方法孔隙度体反演剖面分辨率有了很大提高,对薄砂体也能很好地识别,且与井上吻合较好,能很好地刻画出砂体的横向变化情况,平面上砂体的展布也符合该区的沉积相分布。
随机反演;直方统计;变差函数;相关性分析;孔隙度
0 前言
陆丰13-1油田位于珠江口盆地北部坳陷带,构造是在基底隆起上发育的穹隆背斜构造。该构造形态完整、平缓,呈东西走向的椭圆状。长轴为5.7km~6.4km,南北短轴为3.5km~4.0km,闭合高度为60m~61m,闭合面积为21.5km2~25.5km2,构造倾角在1°~3°之间。油田先前开发的主要含油层段在珠江组中部、下部的块状砂岩,有二个含油层组,其间为一套致密灰岩分隔。灰岩(称第二单元层)之上为上油层;灰岩之下为下油层。而本次储层预测的主要目的层是第三单元层,为深层的恩平组2 790层到2 980层段,其油藏埋深为-2 344m~-2 504m,油层厚度达18m~55m。截至目前为止,深层共钻井八口,但钻遇至最深层2 980的仅有四口。在深层有油气显示共六口井,其中表现最好的是构造高部位的W1井。W1井自2010年1月开钻以来,顺利钻至基底3 506.6m。深层从2 790层至2 980层,含油井段长477m,累计油柱高度为92.5m,油层含油面积达0.2km2~1.6km2,有效孔隙度为16%~20%渗透率在50mD~200mD之间,含油饱和度为35%~55%,这说明在该构造区深层有比较好的高孔、高渗层段。
珠江口盆地陆丰凹陷和惠州凹陷之间的陆丰13-1油田,采用高分辨率三维地震150km2作为目标区,其测网密度为12.5m×12.5m,目的层2 500(2s左右)及以下地层,地震波主频只有约20Hz,分辨率和信噪比都较低,相位连续性较差对深层构造评价和储层预测都相当不利。作者利用Jason软件,对该区恩平组砂泥岩储层进行了多种方法的地震反演处理,反演成果包括波阻抗、孔隙度、伽玛、密度等多种反演结果。作者在本文重点介绍一种地震反演方法,即随机地震反演,并且对其应用效果进行分析。
用一般的地震反演方法进行储层预测,容易受到诸多因素的影响,首先反演结果能否与储层存在良好的对应关系就是一个问题。在该地区,我们通过工区内八口井的波阻抗曲线直方图(见下页图1)上可以看出,波阻抗不一定能够很好地区别砂泥岩,而此时波阻抗反演的结果具有多解性,无法唯一描述储层属性;其次,由于受地震采样率的限制和地震主频及频宽的制约,小于采样率的薄层一般是无法分辨的[1]。
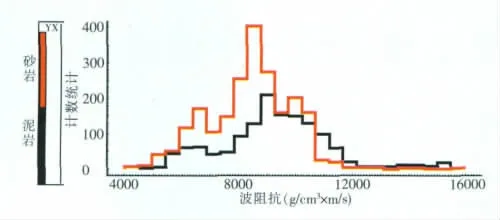
图1 波阻抗曲线直方统计图Fig.1 The wave impedance curve histogram
1 基本原理
随机地震反演结合地质、沉积等方面的知识,以地质统计学为基础,利用测井、地震等各种数据,对沉积环境及空间分布和各种物性参数在空间上的变化进行模拟,然后反演出多个概率实现体。反演主要由两部份组成,即随机模拟过程以及对模拟结果进行优化,并使之符合地震数据的反演过程[2]。随机反演的计算过程如图2所示。
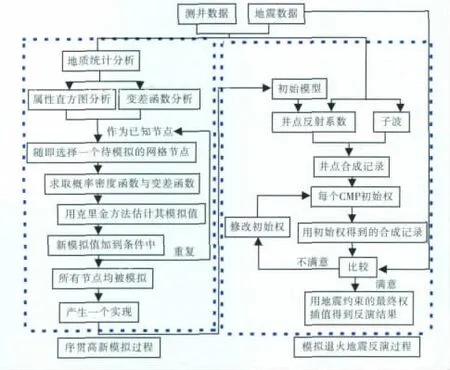
图2 随机反演计算过程Fig.2 Random inversion calculation process
随机反演的关键技术是分析拟合储层物理特性和岩石属性的直方图及变差分布,求出其概率密度函数和变差函数,然后根据其特征选择模拟和反演的方法。变差函数是用来衡量数据的空间相关范围的,它的曲线形态有一定的地质意义。它是计算空间任一长度为h的矢量的头与尾的均方差的二分之一。
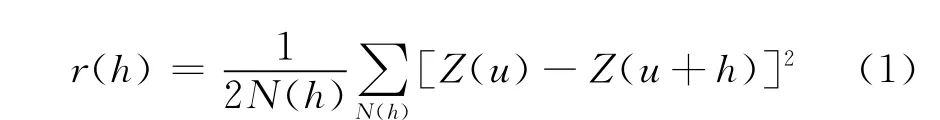
其中 N(h)是在变程值h处的数据对数;Z(u)为在位置u处的参量值(尾);Z(u+h)为在位置(u+h)处的参量值(头)。
为了揭示不同岩性与其属性之间的关系,应分析储层的物理属性特征,如孔隙度、伽玛曲线、密度、波阻抗等,然后根据不同岩性的物理参数分布规律,确定不同岩性的参数门槛值,这样就从定量上解释了储层,这也是储层横向追踪的基础[3]。
地质统计反演方法有其局限性,在反演过程中,应分析反演属性(如密度、孔隙度等变量)与波阻抗之间的相关关系。如果相关性较小,则说明通过波阻抗来反演(或者模拟)测井属性(如密度、孔隙度等)的可靠性较低;反之,则说明运用地质统计反演方法可以对测井属性进行有效预测[4]。
2 应用
在随机反演之前,应首先对资料进行分析,利用已知资料分析确定储层参数的空间分布规律(直方图)和空间相关性(变差函数);然后用不同的地质统计模拟技术来实现储层参数的随机模拟或随机反演。
2.1 储层物性参数相关性分析
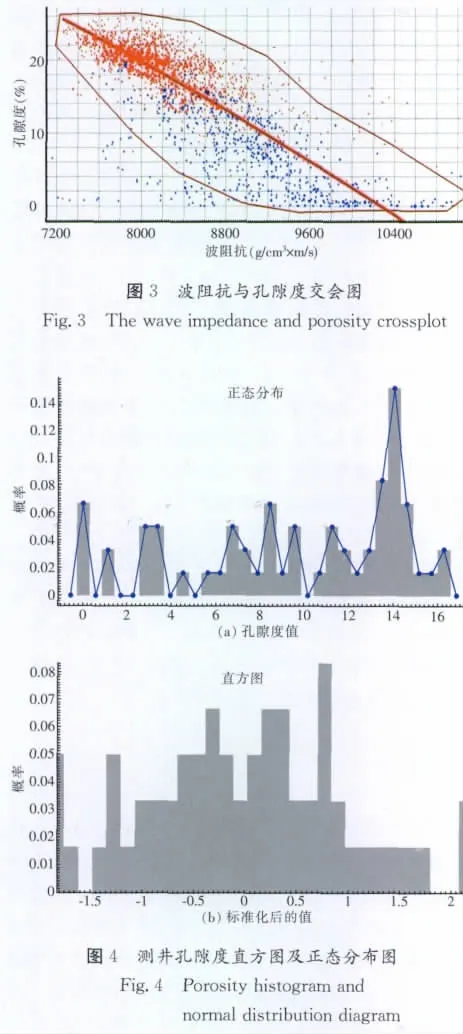
不同电测曲线从不同侧面反映同一岩石的物理性质,它们之间存在一定的相关性和差异性,差异性反映了物理性质不同,相关性意味着它们之间存在一定函数关系。通过将八口测井的波阻抗与自然伽玛、孔隙度等作交会分析,获取不同波阻抗所对应不同的孔隙度概率值。从交会图(见下页图3)中可以看出,波阻抗与孔隙度呈正相关,通过二次方程拟合得到相关系数在0.85以上,说明波阻抗与孔隙度之间的相关性很好,通过这种方法反演得到的孔隙度数据体可靠程度高。
2.2 储层物性参数空间变异性分析
直方图和变差图是随机模拟的两个最基本的工具,直方图是对属性参数一维边缘分布概率密度的估计,从直方图上可以直观地分析属性值分布的总体特征,了解均值、方差、极差等变异情况。图4(见下页)为研究区所有井的2 980层段的孔隙度曲线的统计直方图及正态分布图,从直方图的分布可以看出:该套地层的孔隙度值基本呈对数正态分布,孔隙度在10%~16%之间频数最大。为了更准确地刻画孔隙度体的分布,作者在此次分析中并没使用高斯分布或对数分布来拟合孔隙度体的分布函数,而是使用折线来拟合。这样反演时会首先将该分布函数转换为高斯分布函数进行计算,最后运用反变换将最终的计算结果再转换成原始的分布状态。
变差函数的主要参数有变程(range)、基台(still)和跃迁(Nugget)。基台值是变差函数曲线随h(见公式(1))的增加而上升,曲线由上升到平缓的拐点处的变差值为基台值,它反映了某随机变量在工区的总变差。变程是变差曲线达到基台值的横坐标值,对随机变量的统计沿着X(走向)、Y(倾向)、Z(纵向)三个方向进行,三个方向的变程综合地描述了随机变量的空间相关范围。各向异性变差函数曲线的X、Y、Z方向的变程,反映地下异常体在三个方向的相关范围。由于该研究区处于勘探阶段,现阶段只有八口井,且分布不均匀,所以在运用测井资料计算变差函数的过程中,平面上(X方向和Y方向)的井网密度明显不够,这样确定X和Y方向变程就有了一定的难度。在本研究区,我们采取了这种方法:根据约束稀疏脉冲反演结果,在地震主测线和联络测线上研究沉积体的展布特征,结合沉积体的平面分布特征和地震属性分析结果,定量地确定变量在X和Y方向的变程[5]图5为研究区2 980层变差函数,用变差函数模型进行拟合,基台值为0.71,跃迁为0,Z方向的变程值为7.6m,代表了Z方向区域变量的影响范围。

图5 目的层段孔隙度变差函数图Fig.5 Porosity variation function diagram in destination layer
图6为研究区2 980地层约束稀疏脉冲反演波阻抗沿层切片。经分析认为,红色代表砂体分布特征,通过测量砂体在X和Y方向的分布范围,可以比较精确地确定X和Y方向区域变量的变程大小(X方向2 500m,Y方向1 500m)以及变差函数的方位角(60°)。

图6 2 980层约束稀疏脉冲反演波阻抗均方根属性图Fig.6 Wave impedance RMS attribute map of 2 980layer constrained sparse pulse inversion
2.3 随机模拟及随机反演
我们选取对储层敏感的孔隙度曲线作为储层表征曲线,运用高斯序贯模拟及模拟退火地震反演的反演方法。由于随机模拟是在原始框架模型的限制下模拟孔隙度各种可能的分布,所以在模拟时,用不同的随机路径会有不同的模拟结果。为更真实地反映孔隙度在纵向、横向和平面上的变化,用高斯模拟在地震原始数据的约束下,采用模拟退火的非线性迭代反演方法,这样不但使模拟结果充分利用了井的资料,还能与地震原始资料相匹配。
随机模拟反演较好地解决了地震与测井间的加权和结合,由于模拟结果中随机成份的干扰,必须在十次模拟结果中挑选出合适的概率实现体。我们分别对十套概率体沿层提取时间切片,得到不同时间的孔隙度平面变化关系,将其与地震属性和约束稀疏脉冲反演进行对比,挑出合适的实现体。
2.4 效果分析
分析研究井岩芯观察和实验室资料得知,2 790层段至2 980层段为块状砂岩夹泥岩,是辫状河沉积。油层岩性单一,主要为长石砂岩,岩屑长石砂岩,泥质胶结为主。孔隙类型以粒间孔为主,大孔隙结构。在本次研究中,我们选择了六口井进行反演,其中二口井作为校验井。图7是联井线孔隙度随机反演剖面图,W1井、W2井、W3井、W4井和W5井投的变密度显示的孔隙度曲线,校验井W3投的是曲线形式显示的GR曲线。
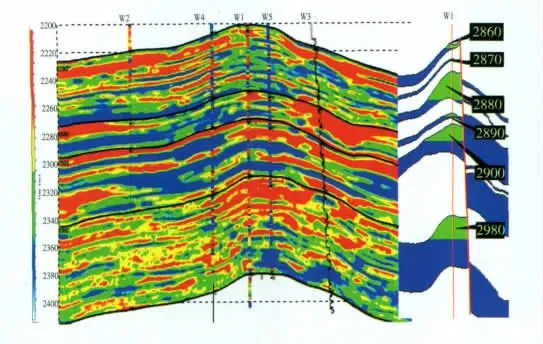
图7 联井线孔隙度反演剖面图Fig.7 The well line cross-section of porosity inversion data
从图7上看,井点之间与反演结果吻合较好,从右边W1井的油层情况可以看出,其与左边的孔隙度反演剖面比较吻合,可以看出孔隙度大于10%为砂岩储层,2 880、2 900和2 980三套砂体都与井上很吻合,孔隙度反演剖面的分辨率比波阻抗剖面高,且与波阻抗的趋势基本一致。从整体来看,砂体的横向变化非常清楚,薄厚变化,砂体尖灭情形等都清晰可见,最小分辨的砂体厚度约为5m,其纵向、横向展布特征清楚。
为了搞清储层的分布范围,对孔隙度数据体沿储层顶面向下作时间切片,得到不同时间的孔隙度平面变化关系。下页图8是随机反演方法得到的2 790层、2 880层、2 900层和2 980层的孔隙度平面分布对比图,可以看出,2 790层砂体储层分布较多,孔隙度最高可达20%;2 980层孔隙度稍低于2 880层和2 900层,有效孔隙度主要分布在W1井和W5井附近。从孔隙度反演的属性平面分布特征来看,2 790层以下地层主要以北东向的物源为主,南部物源为辅的多物源分布特征,从辨状河三角洲沉积过渡到辨状河平原沉积以后,物源逐步转为西部物源为主。
综合分析孔隙度剖面及平面分布,再结合其构造特征,得出了该区西部储层极为发育,平面上具有分区性和分带性,垂向上具有一定的分段性。随机反演预测能力大大提高,能很好地反映砂岩储层的横向和纵向的细微变化。
3 结论
作者在综合分析陆丰13-1油区的地质、构造、沉积特征的基础上,首先论证了利用地震反演方法对储层进行预测的可行性,并对地震反演方法在储层预测中的局限性作了分析,提出要想取得较高的预测精度,必须结合地质、测井、开发等多种资料,进行多种地震反演方法的综合预测的观点。通过本次研究,得出了以下几点认识和结论:
(1)随机反演充分考虑地质统计信息,使储层属性描述结果与地质统计及地震反演双重吻合,很好地反映储层属性空间分布的非均质性和不确定性[6]。随机反演能对多种属性参数反演,筛选出能有效区分储层的属性进行反演,而且其储层分辨能力大大增强。由于本研究区钻井数较少且分布不均匀,所以在反演上有一定的难度,但是随机反演能在一定程度上反映出地震剖面中岩性油气藏的特征,从而可以在反演剖面上较容易地看出砂体的叠置关系,在平面上看到砂体的展布情况;
(2)研究目标的地质特征、钻井数量、井位分布以及地震资料的分辨率和信噪比,对地震反演结果的精度必然有很大的影响,但是选择合适的方法正确处理参数和深入的综合分析,也能很大程度上提高反演的精度。
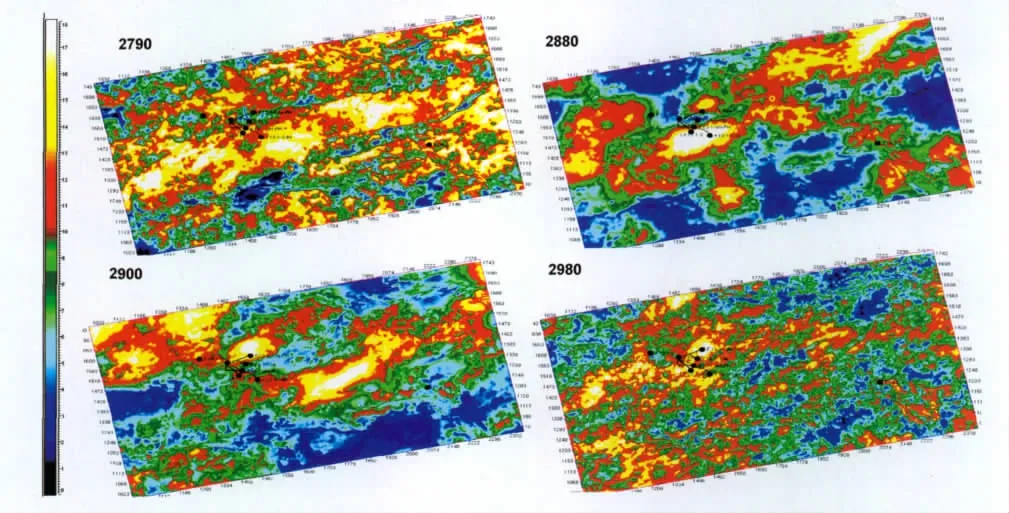
图8 孔隙度平面分布图Fig.8 Distribution of porosity attribute
(3)随机反演能有效地从垂向上提高储层的分辨率,加上充分考虑了地下地质情况的随机性,使反演结果更符合实际地质情形。
[1] 张永刚.地震波阻抗反演技术的现状和反震[J].石油物探,2002,41(4):385.
[2] 王延光.储层地震反演方法以及应用中的关键问题与对策[J].石油物探,2002,41(3):299.
[3] 苏云,李录明,钟峙,等.随机反演在储层预测中的应用[J].煤田地质与勘探,2009,37(6):34.
[4] 徐明华,主心丸,王达明,等.苏里格气田苏5区块储层地震反演预测技术[J].天然气工业,2007,27(12):33.
[5] 李方明,计智锋,赵国良,等.地质统计反演之随机地震反演方法[J].石油勘探与开发,2007,34(4):451.
[6] 李建华,刘百红,张延庆,等.基于井间地震资料的储层精细描述方法[J].石油地球物理勘探,2008,43(1):41.
[7] 郑爱萍,刘春平.随机模拟在储层预测中的应用[J].江汉石油职工大学学报,2003,16(3):34.
[8] 孙思敏,彭仕宓.地质统计学反演方法及其在薄层砂体预测中的应用[J].西安石油大学学报:自然科学版,2007,22(1):41.
[9] 易平,林桂康.随机地震反演技术及在文昌13-1油田的应用[J].石油地球物理勘探.2005,40(1):87.
[10]沈财余,阎向花.测井约束地震反演的分辨率与地震分辨率的关系[J].石油物探,1999,38(4):96.
[11]HANDONG HUANG,RUWEI ZHANG,QUN LUO,et al,Subtle trap recognition based on seismi sedimentology-A case study from Shengli Oilfield[J].Applied Geophysics.1993(2):175.
[12]李廷辉,岳跃龙,胡永军,等.Jason反演技术在张东地区储层预测中的应用[J].石油地球物理勘,2005(S1):108.
[13]年静波,汤磊,刘喜武.地质统计分析在地震资料砂泥岩分布预测中的应用[J].石油物探,2004(3):278.
[14]DUBRULE O,THIBAUT M,LAMY P,et al Geostatistical Reservoir Aracterization Constrained by 3DSeismic Data[J].Petroleum science,1998 4121.
[15]TORRES-VERDIN C,VICTORIA M.Trace-based and Geostatistical inversion of 3Dseismic data fo thin-sand delineation:An application in San Jorg Basin,Argentina[J].TheLeadingEdge,1999:1070.
[16]王根久,赵丽敏,李薇,等.随机建模中变差函数的敏感性研究[J].石油勘探与开发,2005,32(1):72.
book=88,ebook=88
1001—1749(2012)03—0331—05
P 631.4
A
10.3969/j.issn.1001-1749.2012.03.16
刘丹(1986-),女,硕士,研究方向为能源地震勘探,主要从事地震构造解释、属性预测和储层反演等方面的研究工作。
2011-10-19改回日期:2011-10-25

