MT数据处理中静校正方法对比

杨淼鑫，李晓晨，刘小畔

（成都理工大学地球物理学院，成都 610059）

MT数据处理中静校正方法对比

杨淼鑫，李晓晨，刘小畔

（成都理工大学地球物理学院，成都 610059）

在大地电磁测深数据处理中，静态效应会影响解释结果。这里主要采用有限单元法进行正演计算，采用阻抗相位校正法、空间滤波法以及视电阻率导数解释法，对存在静态效应的理论模型进行数据处理。对比结果表明，前二种方法对静态效应起到了一定的压制和改善作用，且阻抗相位校正法效果相对较好，而通过视电阻率导数解释法，可以准确地反映地下真实异常形态。

大地电磁测深法；静态效应；阻抗相位校正法；空间滤波法；视电阻率导数解释法

0 前言

在大地电磁测深中，当地表或近地表存在横向电性不均匀体时，会使地表或近地表附近的大地电流密度增加或减少，具体表现为视电阻率曲线发生向上或向下的平移，但视电阻率曲线形态和相位曲线不会因此而发生改变，这就是静态效应。而由静态效应引起的畸变为静态位移。

在野外实测资料中，视电阻率和阻抗相位等资料一般包括多种干扰影响因素，其中以静态位移影响最为突出，它表现在视电阻率拟断面图上会呈现横向范围不大的陡立密集等值线。由于静态位移影响往往使资料反演解释产生较大偏差，因此在反演解释之前，需要对MT资料进行室内综合处理，其中的主要工作就包括静校正处理。

目前采用的静校正方法比较多，Bostick［2］提出的EMAP法；Andrieux等［4］和Sternberg等［5］提出联合反演法；Larsen［3］作出了理论计算法；Jones［6］提出MT资料的自身校正法；Zonge等［7］提出了曲线平移法；Bailey［9］和杨生等［8］提出阻抗张量分解法等等。这些静校正方法的原理和效果不尽相同，因此应视实际资料情况选择使用。作者在本文主要研究阻抗相位法、视电阻率导数解释法和空间滤波法（五点滤波和七点滤波），并比较了这些方法的校正效果和解释结果。

1 静校正的方法

1.1 阻抗相位校正法

Bostick，K.L.Zonge等人导出过阻抗相位和视电阻率之间的换算关系式：

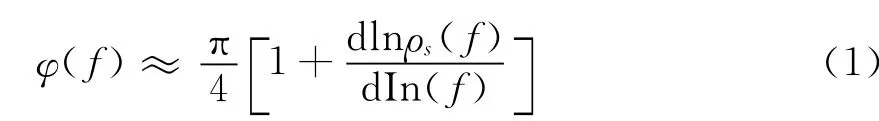
因静态效应不影响阻抗相位，因此我们可以通过相位的计算，来导出不受静态效应影响的视电阻率，经过变换可得到下面的公式：

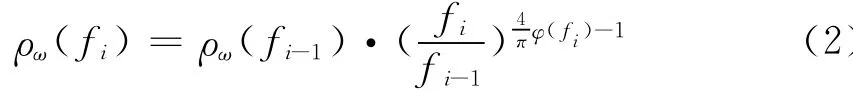
其中 ρω（fi）和ρω（fi－1）为二个相邻频点的视电阻率值，频率由高到低进行换算，初始条件应选择最高频率和表层视电阻率。而最高频率即为实际最高频率，可设置合理的视电阻率值或一条测线表层视电阻率的几何平均值为初始条件的表层视电阻率值。

1.2 空间滤波校正法

空间滤波的基本思想为：沿测线的地下异常体或地质构造所引起的视电阻率是平缓变化的，而静态效应会使其呈现高频特征，采用低通滤波器进行空间滤波，可以消除由静态效应引起的高频异常。

首先，初步判断静态效应存在的频点，选择一个相对稳定的频点段，设为n，则有：

其中 i是测点号；j是频点号；ρi为平均视电阻率值。

五点滤波函数，滤波电阻率值为：

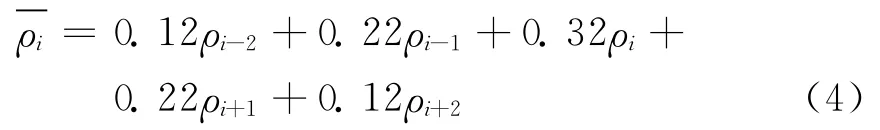
七点滤波函数，滤波电阻率值为：

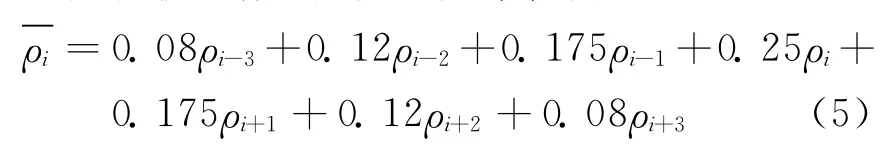
校正系数为：

最后得到新的视电阻率值为：

1.3 视电阻率导数解释法

当受到静态效应影响时，视电阻率曲线呈现为尾支向下，但是视电阻率导数反应的是等值线的横向特性，是不受静态效应影响的，因此可用以下校正公式：

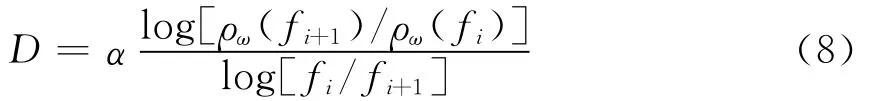
其中 α为大于100的任意常数，D只与各测点的视电阻率曲线形态有关，而与其视电阻率值的大小无关，因而不受静态效应的影响。

用校正后的D作为新的视电阻率值画出等值线，异常体的位置为零值或负值圈闭。

2 算例

作者在本算例中主要采用四边形剖分、起伏地形二维大地电磁正演模拟进行正演计算。

（1）模型一。在电阻率为100Ω·m的均匀半空间中，地表存在长100m、宽40m的地表不均匀体，电阻率分别为30Ω·m和1 000Ω·m（见图1（a））。

图1（b）为均匀半空间中在地表存在不均匀体时的正演图，可以看出，在地表的低阻体和高阻体所在的位置上，均出现了陡立的等值线异常带，造成一种是陡立断层或岩脉的假异常。显然，对TM模式来讲，静态效应的影响范围是从高频一直延伸至低频。

图2（见下页）分别采用了四种不同的方法，对模型一的正演结果数据进行静态位移校正的结果图。对比下页图2中的（a）、（b）、（c）、（d）可以明显看出，阻抗相位校正法和空间滤波法对校正静态效应均具有一定的压制作用。显然，阻抗相位校正法图2（b）的效果较好，而空间滤波法图2中的（c）及（d）为校正不足，这是因为在校正过程中，需要选择合适的滤波系数和窗口宽度，其规律难于把握。通过视电阻率导数解释法（见下页图2（a）），可真实反映地下均匀半空间的形态。

（2）模型二。在上层电阻率为100Ω·m，下层为500Ω·m的地下介质中，作者设置了长100m宽40m的地表不均匀体，电阻率分别为30Ω·m和1 000Ω·m（见下页图3（a））。

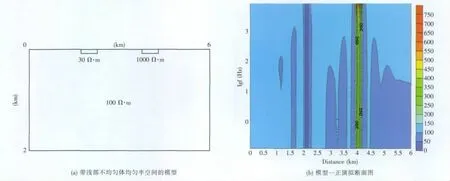
图1 模型一及正演结果Fig.1 Model one and forward result（TM）

图3（b）为层状模型中在地表存在不均匀体时的正演图。可以看出，在地表的低阻体和高阻体所在的位置上，均出现了陡立的等值线异常带，影响了地下层状模型的判断。

通过阻抗相位校正法和空间滤波法的校正静态效应得到了一定的压制，经校正可见阻抗相位校正法图4（b）（见下页）的效果较好，而空间滤波法图4（c）及图4（d）（见下页）为校正不足，这是因为在校正过程中，需要选择合适的滤波系数和窗口宽度，其规律难于把握，但都反映出层状模型。通过视电阻率导数解释法图4（a）（见下页），反映了地下真实异常形态，显示出了地层位置。

3 结论

（1）作者通过用阻抗相位校正法和空间滤波法（五点和七点），分别对二种存在静态效应的模型进行了静校正，从不同程度上都压制了静态效应。而相比之下，阻抗相位校正法效果比较好，空间滤波法因为涉及到滤波系数和窗口宽度的选择，规律比较难于把握。

（2）由于用视电阻率导数解释法对存在静态效应的模型进行解释，能够正确反映地下真实的异常形态，因此，在实际资料处理中，需要不断积累经验，根据不同的情况来选择静校正的方法。

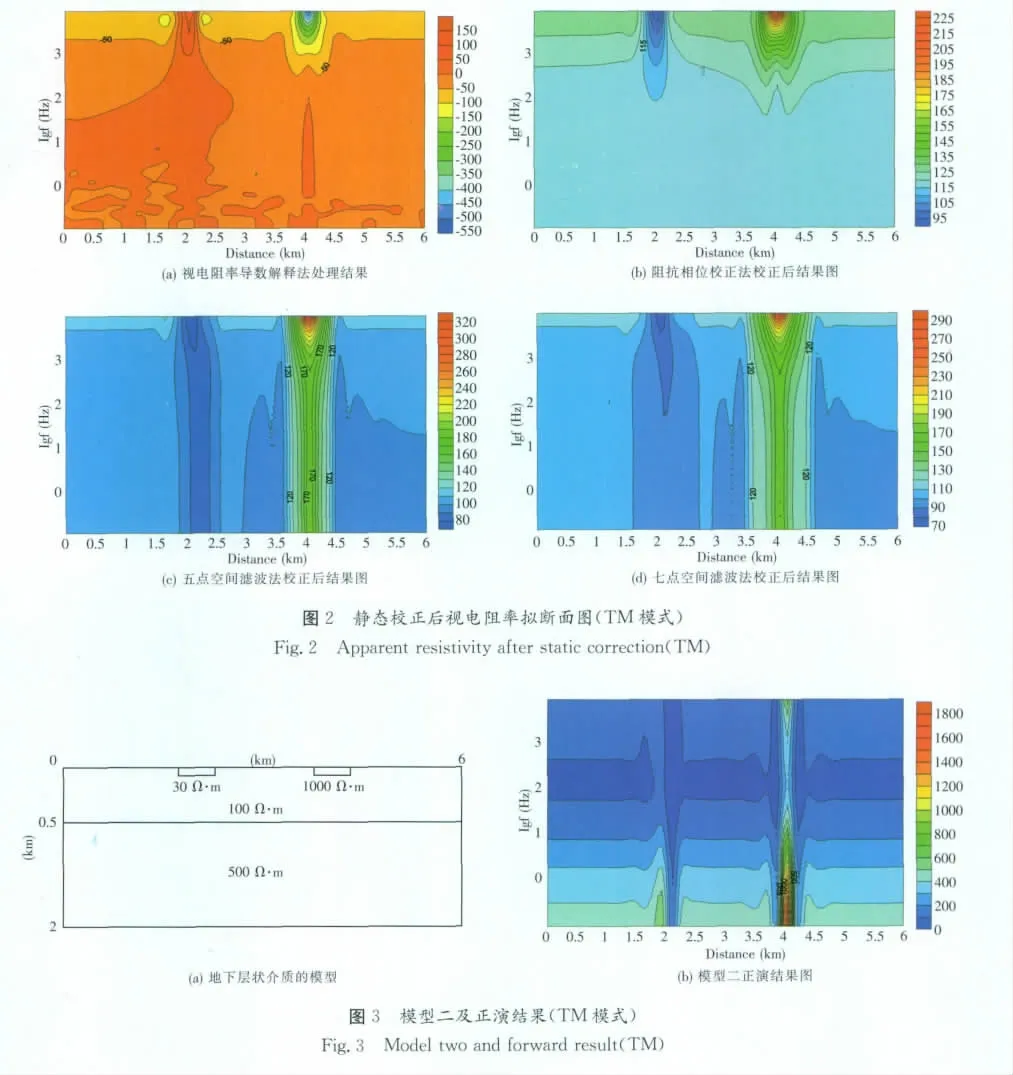
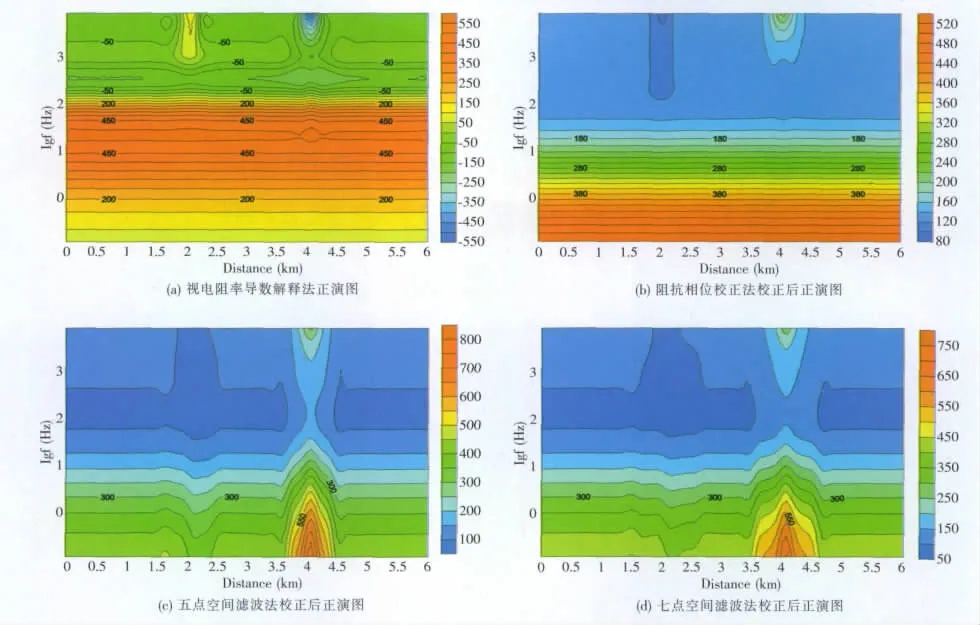
图4 静态校正后视电阻率拟断面图（TM模式）Fig.4 Apparent resistivity after static correction（TM）

［1］ 王家映.关于大地电磁的静校正问题［J］.地质科技情报，1992，11（1）：69.

［2］BOSTICK F X.Electromagnetic array profiling（EMAP）［J］.In：56th Ann Mtg Soc Expl Geophys Expanded Abstracts，1986：60.

［3］ LARSEN J C.Removal of local surface conductivity effects from low frequency mantle response curves.Acta Geodaet［J］.Geophys.et Mantanist.Acad.Sci.Hung，1997（12）：183.

［4］ ANDRIEUX P，WIGHTMAN W E.The so－called static corrections in magnetotelluric measurements［J］.In：54th Ann Mtg Soc Expl Geophys Expanded Abstracts，1984：43.

［5］STERNBERG B K，WASHBURNE J C，PELLERIN L.Correction for the static shift in magnetotellurce using transient electromagnetic sounding［J］.Geophysics，1998，53：1459.

［6］JONES A G.Static－Shift of magnetotelluric data and its removal in a sedimentary basin environment［J］.Geophysics，1988，53：967.

［7］ ZONGE L，HUGHES L J.Controlled Source Audio－frequency Magnetotellurics submittted for inclusion in Nabighian.In：M N，E M Methods in Applied Geophysics［M］.SEG，1998.

［8］ 杨生，鲍光淑.MT法中静态效应及阻抗张量静态校正法［J］.中南工业大学学报，2002，33（1）：8.

［9］ BAILEY R C.Decomposition of magnetotelluric impedance tensors in the presence of local three－dimensional galvanic distortion［J］.Journal of Geophysical Research，1989，94（B2）：1913.

［10］罗延钟，何展翔，马瑞伍，等.可控源音频大地电磁法的静态效应校正［J］.物探与化探，1991，15（3）：196.

［11］黄兆辉.CSAMT方法中静态问题及其相关反演研究［D］.北京：中国地质大学地球探测与信息技术2006.

［12］程云涛.CSAMT静态效应的识别［D］.长沙：中南大学地球探测与信息技术，2008.

［13］陈辉，王春庆，雷达，等.CSAMT法静态效应模拟及其校正方法对比［J］.物探化探计算技术，2007，29（S1）：64.

［14］黄兆辉，底青云，侯胜利.CSAMT的静态效应校正及应用［J］.地球物理学进展，2006（4）：1290.

［15］赵晓鸣，张恩力，米晓利，等.CSAMT资料处理中的静校正问题［J］.工程地球物理学报，2008（3）：311.

book=15,ebook=15

1001—1749（2012）03—0310—04

P 631.3＋25

A

10.3969/j.issn.1001－1749.2012.03.12

杨淼鑫（1988－），女，河北邯郸人，硕士研究方向为地球物理反演与成像。

国家863课题（2009AA06Z108）

2011－07－23 改回日期：2011－11－03