基于遗传算法反求耳结构弹性模量

程向东 姚文娟

(上海大学土木工程系，上海200072)

基于遗传算法反求耳结构弹性模量

程向东 姚文娟*

(上海大学土木工程系，上海200072)

本研究通过力学反问题原理，利用已知的位移求解耳结构弹性模量。随机产生遗传算法的初始种群，使用自编的Matlab算法程序，对初始种群进行遗传迭代计算，把已知的目标位移与种群位移的均方差作为目标函数，以目标函数值最小控制迭代进化的方向。通过耳结构的鼓膜凸和镫骨底板2个控制位移以及砧镫关节周围的8个控制位移这两个算例求解正常砧镫关节的弹性模量，并使用耳结构的鼓膜凸和镫骨底板2个控制位移求解病变砧镫关节的弹性模量。结果表明，使用基于遗传算法的反问题方法计算耳结构的弹性模量是可行的，并且具有稳定性和不受结构力学性能影响的特点，相对误差分别为0.05%和0.2%、0.03%，可为临床病变耳提供有效的力学参数。

耳结构;反问题;弹性模量;遗传算法

引言

随着科学的发展，学科之间的交叉研究已成为新的发展方向。把力学原理应用于探索生命科学是交叉学科研究的典范。20世纪末至21世纪初，耳生物力学研究开始起步，国内外很多学者应用力学原理对耳结构进行研究，其一是解析分析方法，如依据弹性力学原理推导基底膜振动方程［1］，依据变分原理推导耳膜的振动方程［2］，建立检验人工听骨力学性质的解析模型等［3］;其二是有限元数值模拟计算分析，如通过高分辨率计算机辅助断层或组织切片，建立了中耳及全耳的三维有限元模型［4－5］，研究砧骨假体头的尺寸对振动影响［6］，研究镫骨置换假体接头形状对听力传导影响［7］。通过CT扫描建立了中耳及全耳的三维有限元模型，得到鼓膜及听骨链的最大应力区域就是鼓膜穿孔及听骨链病变部位，同时得到人工镫骨较为合理的形体［8－10］，得到外耳道、中耳砧镫关节、内耳淋巴液对传声特性的影响，并得到了鼓膜病变对传声的影响［11－12］。

应用力学原理探索耳结构的研究中的一个必要前提是力学参数的确定，以前研究力学参数的方法是通过对正常人耳进行实验测试得到［13－14］，如弹性模量［15］及本构关系等［16］。在耳结构发生病变以后，其力学参数会发生相应的改变，并且无法对临床病变耳进行复杂的实验研究以获得力学参数，便不能应用力学原理对其进行探索。本研究基于遗传算法，通过耳结构在外力作用下的位移，反求耳结构的力学参数。为无法通过实验测试的病变活体结构力学参数的反演提供了简捷有效的方法。

1 遗传算法基本理论

遗传算法(genetic algorithm，GA)是由美国Michigan大学教授 Holland及其学生于1975年创建，是基于对自然界中生物遗传和进化机理的模仿。对遗传算法基础理论的研究主要分3个方面:模式定理的拓广和深入、遗传算法的新模型和遗传算法的收敛性理论。隐含并行性原理和模式定理被看作是遗传算法的两大基石。Holland给出了模式定理:具有低阶、短的定义长度、模式采样的平均适值在种群平均适值以上的模式，在遗传迭代过程中将按指数增长率被采样。模式定理可表达为

式中，m(H，t)表示第t代群体中包含模式H的染色体，f(H)表示在第t代群体中包含模式H的染色体的平均适应度值，为第t代群体的所有染色体的平均适应度值。L为染色体的长度，Pc、Pm为交叉、变异概率，O(H)、δ(H)为模式位数和模式定义长度。

针对不同的问题，由不同的编码方法和不同的遗传算子就构成了各种不同的遗传算法［17］。遗传算法有诸多优点:直接以目标函数作为搜索信息，并且使用多个搜索点的搜索信息［18］，具有全局搜索能力，不宜陷入局部最优等［19］。

基本遗传算法(simple genetic algorithm)数学模型可表示为［17］

式中，C为 个体编码方法;V为 个体适应度评价方法;pop为初始种群;popsize为种群大小;Φ选择算子;Γ为交叉算子;Ψ为变异算子;Τ为算法终止条件。对于右边的参数和算子，确定好参数 C、pop、popsize、Τ以后，通过算子 Φ、Γ、Ψ 来模仿生物的遗传进化，以V控制迭代进化的方向。

流程图可表示为图1。首先确定编码方式 C，并产生初始种群pop，对种群进行适应度值计算V，然后基于种群个体的适应度值，对种群进行遗传算子Φ、Γ、Ψ操作，使种群不断进化，直至新产生种群中的个体足够优秀。

图1 基本遗传算法流程图Fig.1 Flow chart of simple genetic-algorithm

2 求解思路

基于遗传算法，通过已知位移 un(n=1，2，3，…，k)求解耳结构的弹性模量。如图1所示，基于遗传算法的迭代计算，首先需要产生一个初始种群，然后通过设定的适应度函数对种群的个体进行适应度的计算，基于个体的适应度值，进行选择、交叉、变异算子的操作，使种群往最优解方向进化，每个循环结束后，评价适应度值是否达到最优解，如果未达到最优解则进行下一个循环，直到达到最优停止。

相对于反问题，正问题的求解是成熟的，本文通过耳结构有限元模型来进行正问题的计算，并把计算的参数和结果作为反问题遗传算法的初始种群，本研究用的有限元模型已经验证了正确性［9，10］。

3 程序设计

整个算法的实现包括9个步骤。

步骤1:设置遗传算法参数。编码方式C采用实数编码。种群的大小即种群个体的数量，用popsize表示。种群个体的大小即个体的长度，用nvars表示。最大迭代次数用maxgen表示。交叉算子用pc表示;变异算子用 pm表示;繁殖因子用 pg表示。循环结束的最佳适应度界限值条件用delt表示。

步骤2: 初始种群pop的产生。对耳结构有限元模型赋予不同的弹性模量，计算出不同的位移，把计算的数据保存于 matlab工作目录下，命名为 my_data.txt，其大小为 popsize × nvars。算法程序中导入文件my_data.txt作为初始种群即可。

步骤3:适应度值计算。遗传算子是基于种群个体适应度值进行的，所以先计算种群中个体的适应度值，文中适应度值通过下式计算［19］

种群个体位移 u'1，u'2，…，u'k与目标位移 u1，u2，…，uk的平方差，因为本研究中是找到φ的极小值即认为得到最优解，所以适应度值需要在φ前加一个负号，即适应度值Fit为:

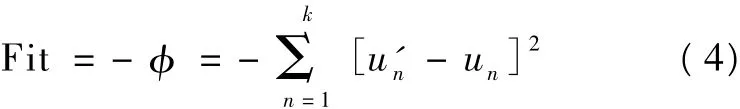
计算出适应度值Fit以后，存放在种群pop的第nvars+1列，然后依次计算每个个体得到的适应度值Fit均存放在每个个体的 nvars+1个位置，适应度值计算完成后，种群 pop的大小变成 popsize×nvars+1。

步骤4:保持最优个体keepbest。保持最优个体函数 keepbest实质上也是一个选择算子［20］。初始种群是随机产生的，初始种群中包含很多个体是具有低适应度，不适合遗传到下一代的个体，但是也有适应度比较高的个体。为了保证最优的个体不会在遗传操作中被淘汰掉，在选择交叉变异算子进行操作前，先进行保持最优个体算子的操作。依次比较种群中每个个体的适应度值大小，把适应度值最大的一个个体存放于popsize+1行，保持最优个体算子计算完成后种群pop的大小是(popsize+1)×(nvars+1)。

步骤5:选择操作。选择算子采用随机竞争选择［17］。选择操作的主要目的是为了避免有用遗传信息的丢失，提高全局收敛性和计算效率。在选择操作中引入繁殖因子 pg(一个操作算子)［21］，来调节竞争种群规模与适应性种群规模的比例。根据达尔文进化论中大量繁殖的概念，将群体分成适应性群体与竞争群体两种，竞争群体的规模远大于适应性群体的规模。这样，除了把适应性群体中的优良基因型延续到下一代，还增加了一些新的基因型，实际上就是使群体包含更多的模式，从而避免陷入局部最优解，减少未成熟收敛机会，增大搜索到全局最优解的可能性［22］。

选择、繁殖的操作过程:竞争种群用 selpool表示，种群大小为(popsize×pg)×(nvars+1)。对适应性种群pop的popsize个个体进行随机选择，每次选择两个个体，然后对所选择的两个个体的适应度值进行比较，适应度值大的一个个体就被提取到竞争种群 selpool，重复操作直到填满竞争种群的popsize×pg个个体。

步骤6:交叉算子。交叉算子采用算术交叉［22～24］，交叉算子的目的:在生物自然进化进程中，交配重组是一个重要环节，两个同源染色体通过交配而重组，形成新的染色体，从而产生出新的个体或物种。按照较大的概率从种群中选择两个个体，交换某些位产生子代，子代继承了父代的基本特征。本算法采用的编码方式是实数编码，实数编码对问题的描述是自然的，一致性的，且精确度较二进制高。算术交叉的表述:两个基因x、y进行算术交叉得到的子代的基因是:

式中，α为一个0～1之间的随机数。

从竞争种群的第一个个体开始，先选定第一个个体，再在竞争种群中另外随机选择一个个体，与选定的个体进行算术交叉。然后选定第二个个体，进行同样的操作，如此依次对竞争种群中的个体进行同样的交叉操作。

步骤7:变异算子。采用均匀变异算子［17］，均匀变异是指分别用符合某一范围内均匀分布的随机数，以某一较小的概率来替换个体编码串中各个基因座上的原有基因值。它使搜索点在整个搜索空间移动，并且比非均匀变异更有效的对某一重点区域进行局部搜索。变异算子的目的:(1)改善遗传算法的局部搜索能力。(2)维持群体的多样性，避免出现早熟现象。变异算子用新的基因值替换原有的基因值，从而可以改变个体编码串的结构维持群体多样性，防止早熟，

从竞争种群的第一个个体开始，先确定变异点，变异点是一个1到nvars之间的随机数，变异点mpoint=round(rand×(nvars+1)－1)，round表示对一个小数四舍五入取整，rand表示随机产生的一个0到1之间的数;然后确定种群的边界，上边界ubound和下边界lbound;变异点的值就变为 lbound+rand×(ubound-lbound)，它表示种群上下边界范围内的一个随机值。如此依次对竞争种群的每个个体进行同样的变异操作。

步骤8:适应度值。选择、交叉、变异算子操作的对象都是竞争种群，3个算子操作结束以后，种群中产生了新的个体，所以对竞争种群进行适应度值的计算。从竞争种群的第一个个体开始，进行与步骤2一样的操作，计算得到的适应度值，存放于个体的nvars+1个位置，即存放于竞争种群的最后一列。

步骤9:精华模型。精华模型也是一种选择操作，使用精华模型的目的是在对竞争种群进行遗传算子操作以后，需要把竞争种群selpool中适应度值较高的个体提取到适应性种群pop中，才算一次循环完成，下一次循环操作是基于这次循环完成以后新产生的适应性种群pop进行的，这样，算法才能进行遗传进化，不断产生较优的新个体，使迭代向最优解逼近。先把竞争种群个体popsize×pg中的前popsize个个体赋予给适应性种群pop，随之将竞争种群中剩下的个体分为pg-1组，然后每组中选取适应度值最高的个体替换pop中的最差个体，适应度值最高的个体的选取方法是:对 pg-1组个体，逐组操作，对于每一组，先对其按照适应度值的大小进行排序，排序后便能找出适应度值最大的个体，用以替代适应性种群pop中的最差值。

以上9个步骤完成以后，便结束了算法的一次迭代，第一次迭代结束以后，算法并没有停止，算法停止的条件Τ是:迭代达到了规定的最大迭代次数或者迭代结果达到了规定误差允许范围以内。从第二代开始，种群的每一代计算是从第5步到第9步，每一次循环结束后，适应性种群pop会被更新。

4 程序框图

图2为程序框图。首先对遗传算法的初始参数进行设置，然后产生初始种群，使用V对初始种群进行适应度值的计算;基于种群的适应度值进行选择算子Φ，交叉算子Γ，变异算子Ψ的操作，产生新的种群;然后使用V对新种群进行适应度值计算，并基于个体适应度值，选取种群中的较优个体及上一代种群的较优个体组成下一代种群，保证新产生的种群的总体优越性。如此重复，直至达到初始设置的算法终止条件Τ。

图2 遗传算法反算耳结构弹性模量程序框图Fig.2 Program chart of genetic-algorithm for inverse derivative of elastic modulus for human ear

5 算例

算例1:变异区域为锤砧关节，参考弹性模量为正常人耳砧镫关节弹性模量0.6 MPa，已知其对应的位移u1和u2。遗传算法程序基本参数为:个体长度nvars=3，位移控制点数 k=2，一个为鼓膜凸，一个为镫骨底板中心，在鼓膜上施加90 dB的压力，选取在1 000 Hz下两点的位移。种群大小popsize为20，即随机选取的弹性模量为20个，那么初始种群大小为20×3的矩阵，如表1所示。最大迭代次数maxgen为500，交叉概率为 pc=0.8，变异概率为 pm=0.01，繁殖因子 pg=4，最佳适应度界限值 delt=0.1 ×10－13。

算例1计算结果:随着迭代次数的增加，种群弹性模量逐渐向靠近参考弹性模量的优解方向变化。在迭代440代以后，弹性模量的值接近于真值弹性模量0.6 MPa，本算法的结束条件是迭代次数达到500代或者适应度值的绝对值小于 delta=0.1×10－13。因为适应度值是使用种群位移与真值位移的平方差来计算的，那么如果适应度值小于一个大于零的很小的数delta，则种群位移相当接近真值位移，便认为此时种群位移对应的弹性模量为最优解。在迭代440代以后，种群趋于稳定，适应度值的绝对值等于4.627 1×10(15＜delta，算法停止，此时得到的种群最优个体弹性模量为0.624 MPa。

表1 算例1遗传算法初始种群Tab.1 Initial population of example1

算例2:变异区域和算例1相同，参考弹性模量为正常人耳砧镫关节弹性模量0.6 MPa，已知其对应的位移 un(n=1，2，…，8)。遗传算法基本参数为:个体长度nvars=9，位移控制点数k=8，取为砧镫关节周围边缘上面的节点，在鼓膜上施加90 dB的压力，选取在1 000 Hz下两点的位移。种群大小popsize为20，即随机选取的弹性模量为20个，那么初始种群大小为20×9，如表2所示、数量单位与表1相同。最大迭代次数maxgen为500，交叉概率为pc=0.8，变异概率为 pm=0.01，繁殖因子 pg=4，最佳适应度界限值 delt=0.1 ×10－12。

算例2计算结果:当算法的终止条件设置为适应度值绝对值达到界限值delt=0.1×10－12时，算法迭代了4代便停止了，因为经过第4次迭代计算，种群中已经有个体的适应度值达到了delt以内，此时最佳适应个体的适应度值是 －5.49×10－14，其绝对值在界限delt之内，最佳个体中对应的弹性模量值是0.64 MPa。当算法终止的界限值设置为delt=0.1×10－13时，迭代次数在达到260次以后，种群不再随着迭代次数的增加而变化，直到到达对大迭代次数500代，种群最优中个体的弹性模量为0.639 MPa。

算例3:变异区域为锤砧关节，参考弹性模量为病变人耳砧镫关节弹性模量0.8 MPa，已知其对应的位移u1和u2。遗传算法程序基本参数为:个体长度nvars=3，位移控制点数 k=2，一个为鼓膜凸位移，一个为镫骨底板中心位移。种群大小popsize为20，如表3所示。最大迭代次数maxgen为500，交叉概率为pc=0.8，变异概率为pm=0.01，繁殖因子 pg=4，最佳适应度界限值 delt=0.1 ×10－13。

表2 算例2遗传算法初始种群Tab.2 Initial population of example2

表3 算例3遗传算法初始种群Tab.3 Initial population of example 3

算例3计算结果:算法迭代450代以后，种群中最优个体的适应度值小于初始设定的 delt，种群个体区域稳定，得到弹性模量0.784 MPa，接近于参考弹性模量 0.8 MPa。

6 分析讨论

算例1中，从初始离散的种群，经过遗传迭代440代以后便找到一个解0.624 MPa，真值弹性模量为0.6 MPa。所采用的初始种群的上限为48 MPa，下限为0.01 MPa，那么在区域 U=0.01～48的范围内求解，得到最优解0.6 MPa的相对误差为:δ1=(0.624－0.6)÷(48－0.01)=0.05%

由于中耳有复杂的力学机理，而文中遗传算法计算反问题的程序是可以排除力学机理等的影响的，为了验证本程序不受力学机理的影响，在算例2中选取的控制位移点是待求砧镫关节周围的节点，以排除听骨链力学的影响。迭代计算求得弹性模量0.639 MPa与参考弹性模量0.6 MPa也非常接近，相对误差为:

为了更进一步验证程序的有效性及稳定性，算例3中取参考弹性模量为病变的砧镫关节弹性模量0.8 MPa，采用与算例1中一样的控制位移及初始种群，设定特定的适应度函数，控制种群进化的方向，对种群进行迭代计算，迭代450代以后得到弹性模量值为0.784 MPa，与弹性模量0.8 MPa的相对误差为

3个算例的计算结果与真实结果的相对误差都非常小，说明本算法是可行的，算例1和算例2的控制位移的不同说明了算法不受结构力学机理的影响，算例1和算例3参考弹性模量的不同说明了算法的稳定性及有效性。根据本研究的结果，学者在对临床病变耳进行研究时，可先通过所提出算法求解出结构的力学参数，然后通过力学原理对结构进行探索，为临床医学提供参考。本算法具有重现性，但是其稳定性不是非常好，以后的研究中需对算法进行改进，提高算法的稳定性。

7 结论

1)使用遗传算法求解耳结构的弹性模量是可行的，所需要的只是不同的弹性模量对应的结构的位移响应。对于其它的力学参数，只要能用正问题求解出相应的位移，便可使用遗传算法通过位移求解出相应的参数。

2)用遗传算法反求结构的材料属性，不受结构力学性能的影响。算例1中所取的位移是鼓膜凸位移和镫骨足板的位移，两者之间是一个完整的听骨链，具有复杂的力学性能;算例2中所取的位移是锤砧关节周围的点，没有复杂的力学性能，但是两个算例的结果非常接近，即不受听骨链力学性能影响。

3)本研究为无法通过实验测试的病变活体结构力学参数的反演提供了简捷有效的方法。

［1］ Pozrikidis C. Boundary-integral modeling of cochlear hydrodynamics［J］.Journal of Fluids and Structures，2008，24(3):336－365.

［2］ 姚文娟，李武，黄新生，等.耳膜振动方程的建立与求解［J］.振动与冲击，2008，27(3):465 －472.

［3］ 姚文娟，李武，李晓青，检验人工听骨力学性质的解析方法［J］.力学学报，2009，41(2):216 －220.

［4］ Lee GF，Chen PR，Lee WJ，et al.Computer aided threedimensional reconstruction and modeling of middle ear biomechanics by high-resolution computed tomography and finite element analysis［J］.Biomedical Engineering，2006，18(5):214－221.

［5］ Gan RZ，Feng B，Sun Q，Three-Dimensional Finite Element Modeling of Human Ear for Sound Transmission［J］.Annals of Biomedical Engineering，2004，32(6):847 －859.

［6］ Gan RZ， ReevesBP， WangXuelin. Modelingofsound transmission from ear canal to cochlea［J］.Annals of Biomedical Engineering，2007，35(12):2180 －2195.

［7］ Tange RA，Grolman W，An analysis of the air-bone gap closure obtained by a crimping and a non-crimping titanium stapes prosthesis in otosclerosis［J］.Auris Nasus Larynx，2008，35(2):181－184.

［8］ Yao Wenjuan， Huang Xinsheng， Fu Lijie， Transmitting Vibration of Artificial Ossicle［J］.International Journal of Nonlinear Sciences and Numerical Simulation，2008，9(2):131－139.

［9］ 姚文娟，李武，付黎杰，等.中耳结构数值模拟及传导振动分析［J］.系统仿真学报，2009，21(3):651 －654.

［10］ 姚文娟，李晓青，李武，等.中耳病变及人工镫骨形体研究［J］.医用生物力学，2009，(24)2:118 －122.

［11］ 刘迎曦，李生，孙秀珍.人耳传声数值模型［J］.力学学报，2008，40(1):107 －113.

［12］ 刘迎曦，李生，孙秀珍.人耳鼓膜病变数值分析［J］.医用生物力学，2008，23(4):275－278.

［13］ Herrmann G，Liebowitz H.Mechanics of bone fractures［M］//Fracture:An Advanced Treatise.New York:Academic Press，1972:772－840.

［14］ Békésy GV.Experiments in hearing［M］.New York:McGraw-Hill，1960.

［15］ Kurokawa H，Richard L.Sound pressure gain produced by the human middle ear［J］.Otolaryngol Head Neck Surg，1995，113(4):349－355.

［16］ Tao C，Rong Z.Mechanical properties of stapedial tendon in human middle ear［J］.Journal of Biomechanical Engineering，2007，129:913－918.

［17］ 雷英杰，张善文，李续武，等.MATLAB遗传算法工具箱及其应用［M］.陕西:西安电子科技大学出版社，2005.

［18］ 徐波，陈晓江.抛物型方程反问题的遗传算法［J］.空军雷达学院学报，2008，22(04):293 －295.

［19］ 蔡传宝，汤文成.遗传算法的生物组织弹性模量反求研究［J］.应用科学学报，2008，26(03):295 －300.

［20］ 曳永芳，杜永清，行小帅.一种抑制早熟收敛的改进遗传算法［J］.山西师范大学学报，2010，24(02):24 －28.

［21］ 田延硕，刘晓云.一种提高局部搜索能力的混合遗传算法［J］.电子科技大学学报，2006，35(02):232 －235.

［22］ 黄卫华，许小勇，范建坤.实数编码遗传算法中常用交叉变异算子的Matlab实现及应用［J］.广西轻工业，2007，(1):77－79.

［23］ 梁昔明，秦浩宇.一种求解约束优化问题的遗传算法［J］.计算机工程，2010，36(14):147 －149.

Inverse Derivative of Elastic Modulus For Human Ear Using Genetic-Algorithm

CHENG Xiang-Dong YAO Wen-Juan*
(Department of Civil Engineering，Shanghai University，Shanghai 200072，China)

The objective of this paper is to calculate the elastic modulus of the ear structure by the known displacement based on inverse problem theory of mechanics.The initial population of the genetic algorithm was generated in random.Genetic iterative calculation was carried out on the initial population by a self－compiling program using MATLAB language.The target function was the mean-square deviation between the known displacement and the displacement of the population.We completed the following work by the calculation example:The elastic modulus of the normal incudostapedial joint was obtained by two controlled displacements of umbomembranetympani and stapesfootplateofhuman ear.Theelasticmodulusofthenormal incudostapedial joint was obtained by eight controlled displacements around incudostapedial joint.The elastic modulus of the diseased incudostapedial joint was obtained by two controlled displacements of umbo membrane tympani and stapes footplate of human ear.Results showed that it was feasible to calculate the elastic modulus of the ear structure by the inverse problem method based on genetic algorithm，which has the advantage of stability and independence of structure mechanical property.The relative errors were 0.05% ，0.2% ，and 0.03%respectively，which supplied valid mechanical parameters for diseased human ear in clinic.

ear structure;inverse problem;elastic modulus;genetic algorithm

R318

A

0258-8021(2012)04-0487-07

10.3969/j.issn.0258-8021.2012.04.000

2012-04-02，录用日期:2012-06-08

国家自然科学基金(11072143);上海市科委基础研究重点项目(08jc1404700)

* 通信作者。E-mail:wenjuan@mail.shu.edu.cn