基于中枢模式发生器控制的电刺激步行康复系统设计与实验
王 颖 张定国
(上海交通大学机械系统与振动国家重点实验室,上海 200240)
基于中枢模式发生器控制的电刺激步行康复系统设计与实验
王 颖 张定国*
(上海交通大学机械系统与振动国家重点实验室,上海 200240)
研发功能性电刺激(FES)康复系统来实现下肢瘫痪病人的行走运动。控制器采用基于中枢模式发生器(CPG)的仿生控制机理。针对基于递归神经振荡器的 CPG模型,研究关键参数(激励性输入、时间常数、感觉反馈、输出阈值)对CPG输出幅值、频率、相位以及占空比的影响。建立包含12个神经元的CPG网络,以控制双腿的4个关节(左/右髋关节和膝关节)和八组肌群(左/右髂腰肌、臀大肌、股直肌和腘绳肌)。所搭建的实验系统和平台,包括悬吊减重系统、助行系统、电刺激系统和运动检测系统。在正常受试者参与的实验中,受试者在CPG控制的电刺激作用下产生非自主行走运动。实验结果表明,受试者双腿的髋关节和膝关节角度与正常人自主行走时的数据达到定性吻合,验证所设计的CPG控制器在FES康复系统中的可行性与有效性。
中枢模式发生器;递归神经振荡器;双足步行;功能性电刺激;下肢康复
引言
脊椎动物广泛存在一种节律运动,它可以不需要意识的参与而自主进行,比如呼吸、游泳、行走、奔跑等。这些节律运动的控制基本是由脊髓的中枢模式发生器(central pattern generator,CPG)完成的。CPG是一种不依赖感觉反馈和上层控制就能自发产生节律性动作模式的生物神经网络[1],能给生物体内负责运动的肌肉群提供节律性的生物电脉冲模式。现代的研究不仅证实了控制人体运动CPG的存在,也研究了它的一些优良特性,比如稳定性和适应性。
CPG的数学模型在工程领域中已经得到广泛的应用[2],尤其是在仿生机器人领域,比如利用CPG实现双足或四足机器人的行走控制[3-5]。康复工程领域则多为研究人工辅助康复性训练与人体CPG的关联性[6-7]。在康复工程领域,有一种靠外界电刺激来训练下肢瘫痪病人行走能力的方法,叫做功能性电刺激(functional electrical stimulation,FES)。经过半个多世纪的发展,目前FES作为一种有前景的技术已得到广泛的认可,并在临床应用中取得了一定的成功[8]。对于 CPG与 FES结合的康复应用技术,现存的研究大多还停留在计算机仿真阶段[9]或动物实验阶段[10]。本研究则把仿真结果转化为实际的人体运动控制实验,进一步验证了CPG在FES康复系统中的有效应用。
1 中枢模式发生器建模
中枢模式发生器的功能是产生节律性的震荡信号,其实际的物理变现形式为神经元的膜电压变化曲线。产生这种震荡信号一般来说归结于两种机制:一种是单独一个神经元的内在震荡膜特性,通常也叫做起搏特性;还有一种是网络机制,归于不同神经元之间的相互关联特性。
从数学角度分析,生物CPG模型真实模拟了离子通道的电化学特征,但是包含了众多参数。由于其复杂性及难控性,很难完整地应用于工程领域,所以必须对模型进行简化,使之成为一个实际可操作的仿生模型。目前,有很多可供选择的简化模型可以借鉴,比如递归神经振荡器(Matsuoka神经振荡器)、相位振荡器、范德波神经振荡器等[2]。本研究基于递归神经振荡器[9],在这种模型中,一个 CPG单元被简化为两个耦合的神经元,并最终将模型简化方程组,有

式中,xi为状态变量(i=1,2),类比于神经元中的膜电压,vi类比于膜电流,yi是神经元的输出,yout是整个CPG的输出,h是两神经元之间交互作用的增益,β是神经元自抑制的自适应增益,r代表激励性输入,e是感觉反馈,L是相应的反馈增益。
一个CPG内两个神经元之间的网络关系如图1所示。

图1 神经振荡器的单元结构Fig.1 Unit structure of a neural oscillator
参照表1的参数设置,在 Matlab-Simulink环境下建立神经振荡器模型,仿真结果如图2所示。注意本文的CPG模型为简化的数学模型,已不同于实际的生物学模型。计算与仿真都是在标准化条件下进行的,所以CPG的参数及输出不具有实际的物理意义,没有量纲。

表1 神经振荡器参数设定Tab.1 Parameters of the neural oscillator
2 仿真结果与分析
CPG输出模式主要包括幅值、频率、相位与占空比等,分别对应于相应节律动作的强度、速度、步态及步幅等运动模式信息。同样,对于递归神经振荡器,也需根据其数学模型的参数,找到与以上研究对象之间的关系。
2.1 幅值特性
在两单元CPG仿真中,通过改变激励性输入的大小来观察输出情况,参照图3(a),输入值如以下规律变化:0~5 s内输入为1,5~10 s内输入为6,10~15 s内输入为 12,15~20 s内输入为 16,20~25 s内输入为30。通过观察不难看出,输入值越大,输出的幅值也越大,但是输出频率几乎没有变化。进一步的分析可以得出,输入值与输出幅值之间近似成线性关系,如图3(b)所示。

图2 神经振荡器仿真结果。(a)状态变量。(b)CPG的输出Fig.2 Simulation results of neural oscillator.(a)State variables.(b)CPG output

图3 激励性输入的影响。(a)激励性输入对CPG状态变量的影响;(b)激励性输入与CPG输出幅值的近似线性关系Fig.3 Effectsof excitation input. (a) Effectsof excitation inputs on CPG state variables;(b)Quasilinear relationship between amplitudes of excitation input and CPG output.
2.2 频率特性
对于单个神经元,在没有任何外界信号作用的情况下,即输入与感觉反馈都为零的情况下,也可能产生震动,即自由震动。在自由震动状态下,根据描述函数法的近似线性处理,在频域计算得[9]
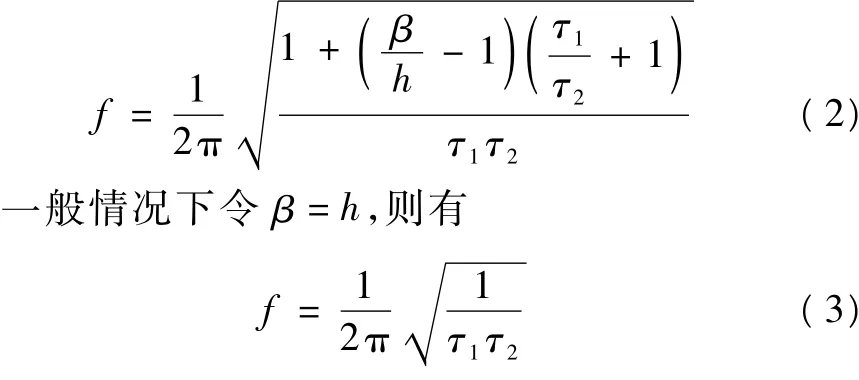

图4 参数 τ1的影响。(a)参数 τ1与 CPG输出频率f间的关系;(b)随参数 τ1的改变,CPG状态变量的频率发生改变Fig.4 Effects of parameterτ1.(a)Relationship between parameter τ1and CPG output frequency;(b) Frequency ofstate variablesvarieswith different τ1
在维持τ2=0.2保持不变的条件下,可以得出τ1- f的关系如图 4(a)所示。当 τ1=0.1、τ2=0.2时,计算得到 f=1.1 Hz,此结果可从图2中得到验证。在两单元 CPG仿真中,通过改变 τ1来观察输出情况,参照图4(b),τ1值如以下规律变化:0~5 s内 τ1=0.1,5 ~10 s内 τ1=0.03,10 ~15 s内 τ1=0.005。经观察可知,输出频率能很好地响应参数τ1的变化,并且严格遵照式(3)的变化规律。不过从图4(b)也发现,参数τ1的变化对CPG输出的幅值略有影响。
2.3 相位特性
感觉反馈是一系列复杂反馈信号的集成,包括力反馈、关节角度反馈和触地压力反馈等。由于感觉反馈的复杂性,在生物CPG中很难摸清楚其对于模式生成的作用,而笔者则着重研究神经振荡器数学模型中感觉反馈的功用。
由于神经振荡器中两个单元间的高度对称性,如果给它们的输入信号完全一致,并且各自的感觉反馈为零,那么震荡就不会产生,CPG也就无法奏效。两单元之间如果存在极其微小的输入扰动,神经振荡器也能产生一个震荡模式,而这个输入扰动就是感觉反馈的作用。然而,输入反馈的值也是有限度的,如果超过一定范围,震荡也会停止,输出值将成为一个非零常量。如果感觉反馈换成为一系列节律信号(比如简单的方波信号),则可以用来控制整个CPG输出的相位与占空比。如图5所示,在感觉反馈信号取幅值为0.5、占空比为50%的方波信号时,CPG的正相输出(正相输出对应于感觉反馈作为正反馈输入的状态变量x1;同理,反相输出对应于感觉反馈作为负反馈输入的状态变量x2)能跟随感觉反馈信号的相位并稳定保持,具体参照式(1)。考察感觉反馈 e存在不同延时的情况下对CPG状态变量的影响,见图5。
研究感觉反馈e的幅值变化对CPG状态变量的影响,见图6。从其中(a)~(c)的纵向比较发现,CPG的正相状态与反相状态在反馈信号幅值增大的同时分别得到加强和抑制,正好可以利用这一点将正相状态单独作为CPG的输出来控制下层系统。当感觉反馈幅值继续增大到10(远大于激励性输入值1)时,跟随情况变得更好,如图6(c)所示。从理论上讲,只要幅值不超过震荡条件的上限,感觉反馈的方波信号幅值越大,其对CPG信号的相位控制能力越强。
2.4 占空比特性
感觉反馈能影响输出信号的相位,同样也会影响输出信号的占空比。如图7所示,在方波信号落回低位时,正相输出能得到迅速抑制,从而较好地跟随反馈信号的占空比。

图5 感觉反馈的延时对CPG的影响。(a)无感觉反馈e;(b)小延时感觉反馈e的影响;(c)大延时感觉反馈e的影响Fig.5 (a)Effect of sensory feedback delay on CPG.(a)No sensory feedback;(b)Small delay of sensory feedback;(b)Large delay of sensory feedback

图6 不同感觉反馈e幅值对CPG的影响。(a)e幅值为1;(b)e幅值为5;(c)e幅值为10Fig.6 Effects of sensory feedback amplitude on CPG.(a)The amplitude is 1;(b)The amplitude is 5;(c)The amplitude is 10
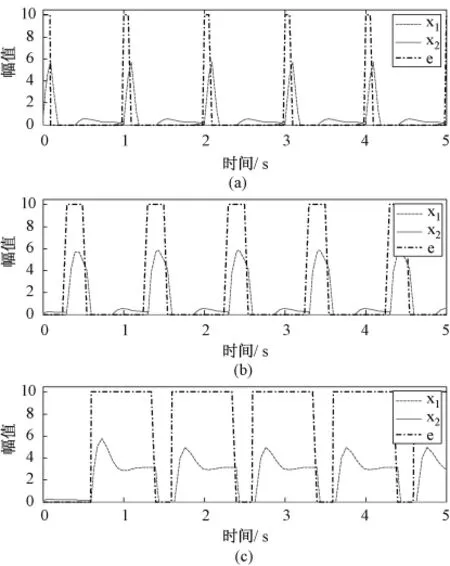
图7 不同感觉反馈信号e的占空比对CPG的影响。(a)e的占空比为10%;(b)e的占空比为25%;(c)e的占空比为50%Fig.7 Effect of sensory feedback duty cycle on CPG.(a)The duty cycle is 10%;(b)The duty cycle is 25%;(c)The duty cycle is 50%
将方波信号作为感觉反馈,可以灵活自如地控制CPG输出的相位与占空比,并最终获得各种所需波形。在实际应用中(比如双足步行),可以将足底触地压力信号稍做处理,将其作为反馈信号输入到CPG的反馈环节中,从而形成一个闭环控制系统,使得CPG的规划更加稳定与准确。

图8 阈值调整CPG的输出占空比Fig.8 Duty cycle adjustments of CPG output by threshold
还有一种基于阈值的方法来调整CPG输出的占空比,即通过调整信号的基准参考来改变激活时间的长短[5]。如图8所示,当阈值为1.7时,正相与反相输出的占空比均为50%;当阈值上升到2.8时,两相输出的占空比也都降到了30%。该方法与感觉反馈参数调整方法都是行之有效的,而且前者可以将一个CPG单元的两相输出都加以利用,不像前述方法那样反相输出得到了抑制,一个CPG单元仅能有一个输出起到模式生成的作用。可以说,两种方法各有优势,本实验环节采用的是感觉反馈参数调整方法。
3 实验与结果分析

图9 实验平台与系统。(a)悬吊系统与助行系统;(b)功能性电刺激系统及电极片;(c)生物传感检测系统。Fig.9 Experimental platform and system.(a)Suspension system and treadmill; (b) FES system and electrodes;(c)Measurement system with bio-sensors
自主搭建了实验平台和系统,如图9所示。图9(a)是实验平台,主要包括悬吊系统与助行系统两大部分。悬吊系统通过卷扬机及一组滑轮,将人体的部分质量悬吊于支架上,从而减轻自重对下肢的负荷;助行系统则是一台跑步机,其跑带的速度与行走速度保持一致,从而确保实验可以在小范围环境内长时间进行。图9(b)是Compex Motion电刺激仪,还有配套的皮肤表面电极片与连接线。图9(c)是Biometrics生物传感系统,包括角度仪、足底压力开关和肌电仪。整体构成了最终实验的功能性电刺激系统。
采用Labview平台作为CPG软件运行环境搭建的CPG网络,可以有效地操控电刺激器对人体肌肉进行外部电刺激,如图10所示。

图10 CPG网络Fig.10 Schematic diagram of CPG network
整个CPG网络的左右两部分始终锁定在180°的相位差,这样能保证人的两条腿不会产生不协调的动作。CPG网络的两边各有3个两单元神经振荡器,1~3构成网络的左半部分,4~6构成网络的右半部分。所有6个振荡器单元都接收到各自的输入信号,这些输入信号可以控制整个网络的开始与停止,并能决定CPG输出的幅值。
根据下肢行走时肌电信号的分析结果[11],将一个步态周期内各个肌肉组的激活时序作为电刺激时序。每个CPG单元在相应的方波信号引导下生成特定相位及占空比信号,再通过不同CPG振荡器单元之间的线性组合,最终形成CPG的输出曲线。通过电脑接口与 Compex Motion电刺激仪的结合,直接线性控制每条电刺激通路的刺激强度。
图11为具体的实验情况。在实验平台上,将上述电刺激器驱动曲线输入到Compex Motion电刺激仪上,在健康受试者上做步行实验。电刺激仪将根据GPG的输出曲线对髂腰肌、臀大肌、股直肌、腘绳肌这4组肌肉(群)进行有序电刺激。从图11(b)~(c)可以看到膝关节两对肌肉上面的电极片布置,髋关节肌肉的电极片被短裤遮盖。膝关节及髋关节均贴有Biometrics角度仪来采集步行过程中的关节角度,足底有压力开关来测量基本步态。CPG控制电刺激的节律周期是1.6 s,对应于跑步机的跑带速度为2 km/h。

图11 正常受试者进行电刺激实验测试。(a)受试者进行实验;(b)下肢正面;(c)下肢背面。Fig.11 FES experimental testing on healthy subject.(a)Overview of the subject under experiment;(b)Front view of lower limbs;(c)Back view of lower limbs
图12 为实验结果,显示了径向平面内4个关节角度变化与两条腿步行状态的对照情况。其中将一个步态循环内的步行状态放大做了步态分析。由于使用的是足底压力开关,测量结果显示的是二值量(0和1):脚部触地的值为1,摆动时的值为0。从图12(c)可以看出,电刺激下的步行运动比较完整地保留了步态循环内的各个部分,包括初始触地、加载响应、站立中期、站立终期、预摆动、开始摆动、摆动中期、摆动终期。
图13(a)为本系统电刺激实验中下肢4个关节的角度曲线,图13(b)为正常步行状态下采集到的4组关节角度曲线。从图中可以看出,在CPG控制的电刺激作用下,受试者的关节角度在定性范畴上与正常人行走的角度数据弥合良好,这在FES领域已经是很好的结果。如果想进一步提高控制精度,需引入闭环FES控制技术。实际上,在三维空间内精确控制人体的行走是个非常具有挑战的难题。在现有FES技术水平下,目前国际上无任何研究者能在实验层面上实现步行运动中多个关节角的定量弥合。

图12 功能性电刺激步行实验结果。(a)下肢各关节角度及足底压力开关值;(b)一个步态周期的足底压力开关值;(c)1个周期内针对右脚的步态分析Fig.12 Results of FES walking experiment.(a)Joint angles of lower limbs and switch values of foot plantar pressure;(b)Switch values of foot plantar pressure during a gait cycle;(c)Gait analysis in a cycle regarding right foot
4 结论
笔者将CPG控制方法与临床医学中比较成熟的FES技术相结合,对脑卒中、脊髓损伤等下肢瘫痪患者的康复训练提出了新的自动化解决方案。研究了基于神经递归振荡器CPG的关键属性,开展了基于CPG理论的功能性电刺激实验。实验结果表明,用CPG网络作为FES系统的核心控制器,能使正常受试者产生比较理想的非自主行走运动,验证了所设计系统的可行性与有效性。未来将深入研究如何优化CPG的参数来调整电刺激下的步速、步态变化等,为不同要求下的康复训练提供更为简单和高效的实现方法。同时,也将开展基于下肢瘫痪受试者的康复实验研究。

图13 基于CPG控制的功能性电刺激实验结果与正常步行情况的对照。(a)电刺激作用下的步行过程中下肢4个关节的角度;(b)正常步行过程中下肢4个关节的角度Fig.13 Results of walking in CPG controlled FES experimentin comparison with normal walking.(a)Four joint angles of lower limbs during walking via FES;(b)Four joint angles of lower limbs during normal walking
[1] Grillner S.Neurobiological bases of rhythmic motor acts in vertebrates[J].Science.1985,228:143 -149.
[2] Ijspeert A.Central pattern generators for locomotion control in animals and robots:A review[J].Neural Networks,2008,21:642-653.
[3] 陈启军,王国星,刘成菊.基于中枢模式发生器的机器人行走控制[J].同济大学学报(自然科学版).2010,10:1534-1539.
[4] 郑浩峻,张秀丽,关旭,汪劲松.基于生物中枢模式发生器原理的四足机器人[J].清华大学学报(自然科学版).2004,44(2):166-169.
[5] 黄博,姚玉峰,孙立宁.基于中枢神经模式的四足机器人步态控制[J].机械工程学报.2010,46(7):1-6.
[6] 王文威,潘翠环,陈艳,罗兆良,罗丽娟.步态中枢模式发生器对脑卒中偏瘫患者步行能力的影响[J].中国康复医学杂志.2011,26(6):529-532.
[7] 寺澤健,常冬梅,李德盛.脑卒中后遗症的步行功能康复[J].中国康复理论与实践.2011,17(9):813-817.
[8] Lynch CL and Popovic MR.Functional electrical stimulation:Closed-loop control of induced muscle contractions[J].IEEE Control Systems Magazine,2008,28(2):40-50.
[9] Zhang Dingguo,Central pattern generator based control for human lower limb movements with functional electrical stimulation[D].Nanyang Technological University.Singapore,2007.
[10] Guevremont L,Norton JA,and Mushahwar VK.Physiologically based controllerforgenerating overground locomotion using functional electrical stimulation [J]. Journal of Neurophysiology,2007,97(3):2499-2510.
[11] Zajac FE,Neptune RR,Kautz SA,Biomechanics and muscle coordination of human walking Part II:Lessons from dynamical simulations and clinical implications[J].Gait and Posture,2003,17:1-17.
A Walking Rehabilitation System Using Electrical Stimulation Based on Central Pattern Generator Control:Design and Experiment
WANG Ying ZHANG Ding-Guo*
(State Key Laboratory of Mechanical System and Vibration,Shanghai Jiao Tong University,Shanghai 200240,China)
A walking rehabilitation system for paralyzed patients using functional electrical stimulation(FES)technique was developed in this work.A kind of biological motor control mechanism,central pattern generator(CPG),was adopted as the controller of the system.Targeting the CPG model named as recurrent neural oscillator,the effects of CPG parameters(excitation input,time constant,sensory feedback,and output threshold)on output amplitude,frequency,phase,and duty cycle were studied.The CPG network containing 12 neurons was developed in order to control four joints(left/right hip joints and knee joints)with eight muscle groups(left/right iliopsoas, glutaeus maximus, rectus femoris, and hamstrings) of lower limbs. FES experimental system and platform is constructed,which includes suspension system,treadmill,FES system and motion measurement system.Experiments were conducted on healthy subjects to generate the involuntary walking movements via FES based on CPG control.The experimental results show that the hip and knee joint angles measured on subjects under FES qualitatively match the data from normal persons during voluntary walking.The feasibility and efficiency of the CPG controller proposed for FES system is validated.
central pattern generator;recurrent neural oscillator;bipedal walking;functional electrical stimulation,lower limb rehabilitation
R318.08
A
0258-8021(2012)04-0558-08
10.3969/j.issn.0258-8021.2012.04.00
2012-01-10,录用日期:2012-04-09
国家自然科学基金(51075265);国家重点实验室基金(MSVMS201112),上海市科委基础研究重点项目(09JC1408400)
* 通信作者。 E-mail:dgzhang@sjtu.edu.cn

