基于H∞控制理论的电动负载模拟器多余力矩抑制

朱光华 ，韩 山 ，闵 斌，余祖铸

（1.上海航天技术研究院，上海 201109；2.上海航天控制技术研究所，上海 200233）

0 引言

负载模拟器是用于仿真飞行器在飞行过程中其舵机所受空气动力力矩的地面实验设备，是典型的被动式力伺服系统。随着国防和工业的发展，对其性能指标的要求越来越高。动态加载过程中，由舵机运动引起的多余力矩会严重影响系统的加载精度，也会使系统的稳定性变坏、频宽变窄、加载灵敏度降低。因此，克服多余力矩是设计负载模拟器、改善系统控制性能的关键［1－3］。CKJ－20控制舱负载台的电动负载模拟器可在动态过程中对控制舱电动舵机施加负载力矩。它由被测产品固定装置、测量装置和加载装置组成，其中控制舱为被测试产品。弹性加载通过弹性扭杆实现，常值加载（恒力矩加载）通过控制加载电机实现。本文以CKJ－20控制舱负载台的电动负载模拟器为研究对象，应用H∞控制理论抑制多余力矩，对系统建模、频响辨识和控制器设计等进行了研究。

1 系统建模与频响辨识

本文中，根据设计指标，主要对控制舱负载台进行恒力矩加载测试，即舵机的常值力矩输出。具体来说，是在舵偏角范围（－25°～＋25°）内，舵偏速度为任意角速度（0～2 000（°）／s）时，可将大小1～7N·m、精度0.5N·m的恒值力矩加载于舵回转轴。力矩波动误差不大于0.5N·m，两侧加载对称性偏差不大于3%，连续工作时间不小于2h。该设计指标是根据吹风实验提出的。实验发现：与传统弹性负载不同，当该导弹的舵面发生偏转时，所受的干扰力矩与舵偏角表现为较严重的非线性。经测量，在最恶劣条件下，此力矩约6N·m。考虑一定的余量，设计一大小为7N·m的恒力矩作为实验中的最大加载力矩，这样即可完全模拟舵机所受的最大负载，从而实现负载性能测试。

为实现恒力矩的加载，须抑制由舵机主动运动造成的多余力矩。工程中，多余力矩常指加载系统不加任何补偿或控制措施，加载指令设为零，此时由加载对象运动时在加载系统输出端表现的力矩，即多余力矩是由加载对象的运动带动加载系统转动产生的感应电势形成的电磁力矩。如忽略加载系统的非线性因素而将系统视为线性系统，多余力矩在数值上等于加载系统为跟随加载对象的主动运动而消耗的控制量在单独作用到加载执行机构上（此时加载机构输出端连接在刚度无穷大的固定机构）产生的力矩输出［3］。

1.1 电动负载模拟器模型建立

电动负载模拟器是一种被动式力矩伺服系统，其模型一般可简化为图1所示的开环框图。图中：Vin为电机指令信号；Va为加载电机控制电压；KV为放大系数；R为电枢电阻；L为等效电感；Km为负载电流到输出电磁转矩的系数；M为加载电机的电磁转矩；J为加载系统转动惯量；为电机角速度，θi为被测舵机角位置；TA为扭矩传感器刚度系数；Mf为扭矩传感器可测量的负载力矩；Ke为电机感应电势系数；s为拉氏算子。

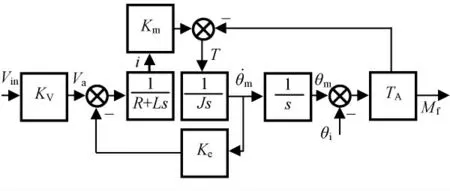
图1 电动负载模拟器系统开环框图Fig.1 Open－loop system diagram of electric load simulator

本文中，选用一台永磁直流力矩伺服电机作为加载电机。Vin经KV与反馈力矩信号的数值匹配，可得

在工作频带内，将直流力矩伺服电机的电枢绕组视为L，R的串联体。则可得加载电机的电压平衡方程为

式中：Vemf为电枢感应电势；i为电枢电流。由Ke，可得

由Km可得

由TA和视为干扰的θi可得θm之差满足

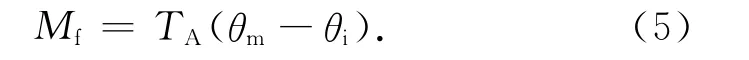
根据上述假设条件和J，加载电机的力矩平衡方程为

合并式（1）～（6），并作拉氏变换，可得负载力矩

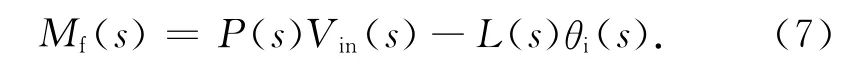
式中：

将实际系统各参数数值代入，得

1.2 电动负载模拟器频响辨识

完成系统的理论建模后，为检验该数学模型的准确性，对频率响应进行辨识。本文采用经典的频率响应辨识方法，用单频正弦信号作为激励，逐频点测试系统对正弦激励的响应特性。

a）加载系统输出端自由运动，使Mf为零。代入式（7），可得

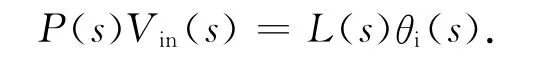
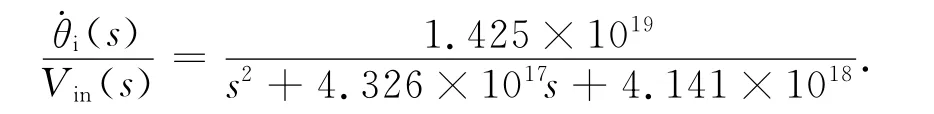
b）加载系统输出端用刚性机构固定，使θi为零。代入式（7），可得

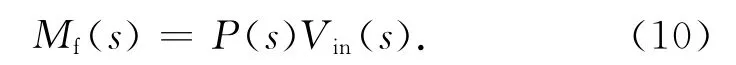
通过一组Vm，Mf间的频响关系，可拟合得

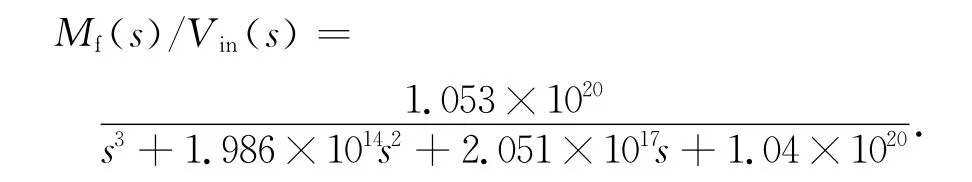
最终，整理后有

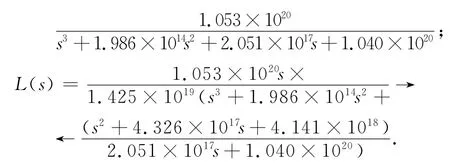
由上述结果可知：通过理论建模和频响辨识获得的系统传递函数阶次较高，形式较复杂，不利于进一步的设计，需作简化处理。在对扰动通道L（s）的仿真中发现，其分子的加加速度项所占比重较小，对系统的影响有限。从设计补偿算法的角度看，只要对速度项和加速度项进行有效补偿，就能很好地抑制多余力矩的影响，达到控制系统的设计要求。因此，在建模过程中，可将此加加速度项舍去以简化L（s）的表达式。其次，分析原系统中力矩输出前向通道P（s）可知：实轴上有一个相对远离虚轴的极点。根据主导极点概念，可将该极点舍去，保留另一对共轭极点。由此，最终所得简化传递函数为

由频率特性曲线可验证，频响辨识获得的结果与理论建模基本一致，但由于系统刚度和摩擦力等的影响，两者仍存在微小的差异，这也正是纯理论建模的局限性所在。因此，下文分析均以频响辨识的结果作为设计及仿真的依据，提高设计系统的准确性。

2 H∞控制理论应用

2.1 经典控制方法简介

电动负载模拟器控制的关键是消除由舵机自身转动产生的多余力矩。多余力矩的产生，从本质上来说是源于位置的扰动，从形式上可视作是由θi通过L（s）产生的，作用点在加载系统的输出端。前人研究中的主要控制方法是根据结构不变性原理，加入一基于扰动的前馈补偿器以消除多余力矩。具体来说，本文在位置扰动与原系统执行机构前加入一补偿控制器Gc（s），使扰动产生的作用与经该控制器后产生的效果抵消，从而实现抑制扰动［4］。加入这种控制网络后的系统如图2所示。

该控制方法可一定程度消除系统的多余力矩，当扰动频率较低时，其控制效果较好，但当扰动频率提高时，控制精度很难提高。对此，可考虑采用H∞控制。

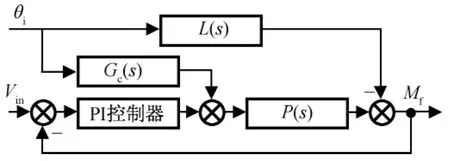
图2 基于扰动的补偿中系统闭环框图Fig.2 Closed－loop system diagram of compensation algorithm

2.2 被控对象的状态空间实现

由前文分析已得系统的传递函数为Mf（s）＝P（s）Vin（s）－L（s）θi（s）。在H∞控制中，选用输出反馈的H∞控制，需建立被控对象的状态空间描述［5－7］。

取加载电机的转动角位置为系统状态x，控制信号为u，干扰信号为w，系统被控输出z为测量信号，即y＝z。因扰动通道L（s）的分子与分母同阶，直接用状态空间描述较复杂，且会不符合输出反馈H∞控制的假设条件，故需对L（s）作调整。考虑系统的扰动信号θi（s）为正弦信号，其一阶微分仍为正弦信号，仅振幅不同，则L（s）可简化为

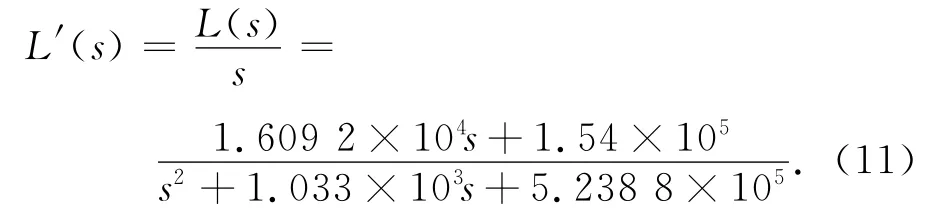
由物理意义可知：该处理法是用角位置的微分信号取代了角位置信号作为干扰的输入，完全可符合性能指标。

由增广矩阵可得系统的状态空间描述为

式中：x1＝－5.236×105；x2＝－1.033×103。

2.3 H∞控制器设计

在扰动抑制问题中，标准H∞控制就是求取一正则控制器K（s），稳定系统闭环内部，且使原系统从干扰输入w到可控输出z的闭环传递函数Gzw（s）的H∞范数极小。本文用Riccati方程解法求H∞设计问题的解，其解由两个与广义被控对象同阶次的代数Riccati方程的解共同构成。

考虑一由状态方程描述的线性定常系统

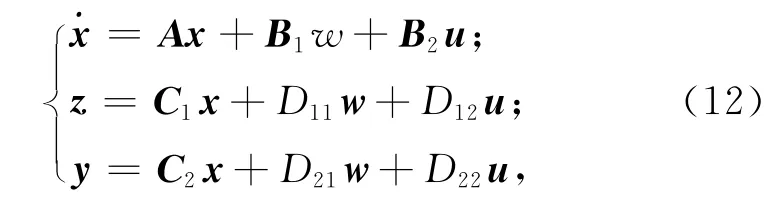
Riccati方程解法如下：设系统的设计指标为‖Gzw（s）‖∞＜γ（此处γ＞0），反馈控制率为u（s）＝K（s）y（s），若控制器K（s）存在，则

a）存在正定对称阵P＝PT＞0，满足Riccati方程

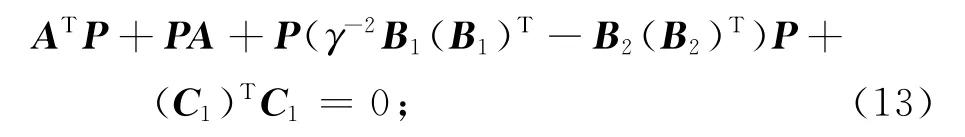
c）P，满足

式中：D11，D12，D21，A，B1，B2，C1，C2为常数项系数；I为单位阵。当满足上述条件时，可得K（s）＝－（B2）TP。实际应用中，整个计算过程可由计算机完成，最终解得

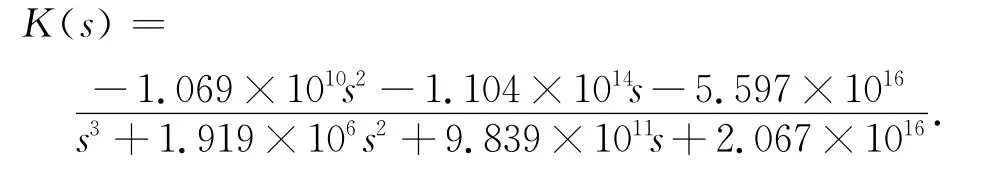
此时最优解γ＝0.3460。

由于该控制器在系统的反馈通路中，常数项系数之差势必会导致反馈增益，不利于稳态调节。因此尝试将K（s）分子的常数项调整为与分母一致，而将增益改在扰动前的前向通路中补偿。则，将控制器改写为

作此调整，并不影响控制器的零极点分布，系统稳定性不受影响。

最后，调整比例积分（PI）控制器的比例环节，补偿闭环系统的控制增益。

2.4 系统仿真

将所得的K（s）代入系统，建立闭环网络，在Simulink软件中进行仿真并与基于扰动的前馈补偿器进行比较。

仿真中，输入信号幅值为1的阶跃信号模拟实际指令。因调整模型中的KV，故仿真输出大小无须与实际电压对应。取幅值为1亦为便于观察，且不失一般性。取干扰信号幅值0.003、频率0～15Hz的正弦波，以模拟实际位置扰动，仿真结果如图3～5所示。

图3 扰动信号频率5Hz时系统的仿真输出Fig.3 System simulation output with frequency of disturbance 5Hz

图4 扰动信号频率10Hz时系统的仿真输出Fig.4 System simulation output with frequency of disturbance 10Hz

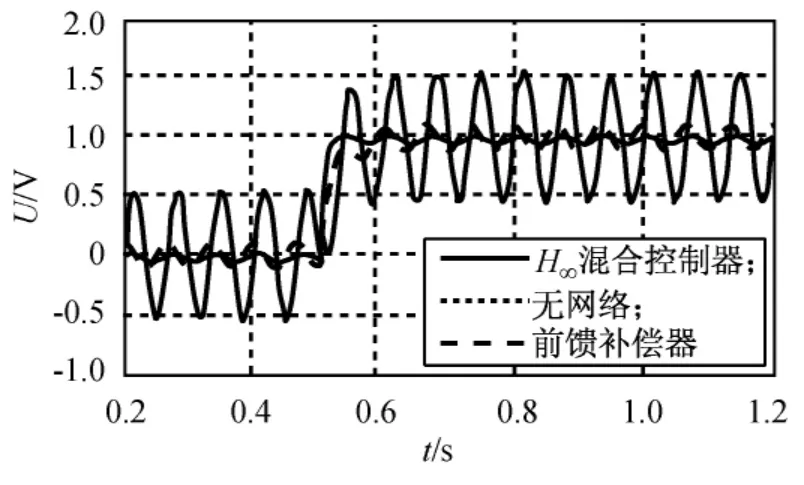
图5 扰动信号频率15Hz时系统的仿真输出Fig.5 System simulation output with frequency of disturbance 15Hz

由图3～5可知：对消除低频扰动信号（5Hz），H∞控制器与基于扰动的前馈补偿器效果相当，但随着扰动信号频率的增大，H∞控制的效果越来越明显。

2.5 H∞控制器与扰动补偿混合使用

经典控制方法中，基于扰动的前馈补偿器是根据结构不变性原理而得，其存在仅是增加了一补偿通道，并未改变系统结构，特别是对前向通道无影响。这种补偿减小了从干扰输入w到可控输出z的“能量”放大倍数，实际上利于H∞控制器的设计。因此，本文综合了两种控制（如图6所示），称之为H∞混合控制器，并测试其控制效果。

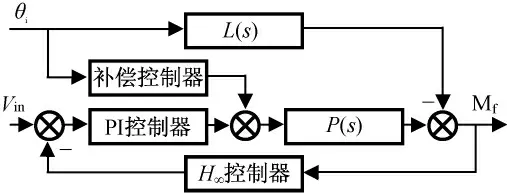
图6 混合控制器网络Fig.6 Combination controller diagram of system

用相同信号对H∞混合控制器进行测试。仿真结果如图7～9所示。由图可知：加入H∞混合控制器后，控制效果继续改善，在低频和高频段，该系统均有响应快、抗干扰能力强和输出稳定等特点，H∞混合控制器的作用非常明显。

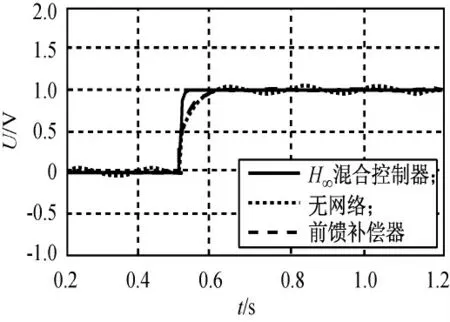
图7 扰动信号频率5Hz时系统的仿真输出Fig.7 System simulation output with frequency of disturbance 5Hz

图8 扰动信号频率10Hz时系统的仿真输出Fig.8 System simulation output with frequency of disturbance 10Hz

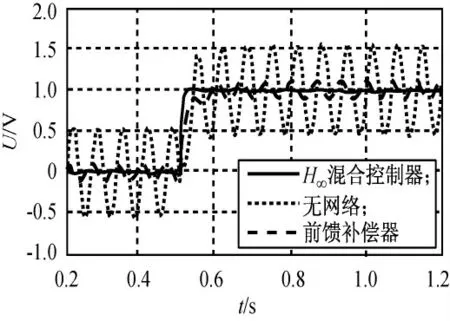
图9 扰动信号频率15Hz时系统的仿真输出Fig.9 System simulation output with frequency of disturbance 15Hz

3 结束语

本文对CKJ－20控制舱负载台的电动负载模拟器系统的组成、特性、控制及其实现进行了研究。基于建立的数学模型，分别应用经典控制中的结构不变性原理和鲁棒控制中的H∞控制对扰动进行抑制，并通过数字仿真和工程实践对这两种控制方法的有效性进行了比较。研究结果表明：H∞控制理论对多余力矩抑制的作用明显。如将两种控制方法综合使用，可获得更好的控制效果。由此，提出了一种H∞混合控制器，可用于被动式力伺服系统。

［1］王 成，王广怀.负载模拟器多余力抑制的探讨［J］.机械工程师，2003（12）：38－40.

［2］朱 伟.电动负载模拟器控制方法研究［D］.西安：西北工业大学，2005.

［3］方 强.被动式力矩伺服控制系统设计方法及应用研究［D］.哈尔滨：哈尔滨工业大学，2006.

［4］任广宁，王少平.电动负载模拟器的多余力矩补偿分析［C］／／中国航空学会液压气动专业2005年学术讨论会.北京：中国航空学会，2005：204－205.

［5］姜长生，孙隆和，吴庆宪，等.系统理论与鲁棒控制［M］.北京：航空工业出版社，1998：366－407.

［6］梅生伟，申铁龙，刘康志.现代鲁棒控制理论与应用［M］.北京：清华大学出版社，2008：94－130.

［7］贾英民.鲁棒H∞控制［M］.北京：科学出版社，2007：57－106.