供给与需求不确定的离散交通网络设计模型

陆化普 李 悦 蔚欣欣

(1清华大学交通研究所，北京 100084)

(2交通运输部规划研究院，北京 100028)

供给与需求不确定的离散交通网络设计模型

陆化普1李 悦1蔚欣欣2

(1清华大学交通研究所，北京 100084)

(2交通运输部规划研究院，北京 100028)

考虑到交通规划中供给需求及决策准则的不确定性，提出了一种基于不确定理论的离散交通网络设计模型.首先，假设供给和需求为随机变量，使用半标准差和风险价值来度量不确定性，建立了考虑决策者风险态度的多目标双层优化模型.随后，使用基于帕累托概念的SPEA2算法对网络优化模型进行求解.以研究中常用的Nguyen-Dupuis网络作为算例进行计算，结果表明:引进风险价值可以有效度量交通规划中决策者的风险态度;多目标规划中不同目标之间存在替代关系;增加建设资金可以有效提高网络性能，但是当投入资金增加到一定额度以后，改善效果并不明显.

离散交通网络设计;供给与需求不确定;风险态度;风险价值;双层模型

传统的双层模型交通网络优化方法缺乏对决策中存在的不确定性的考虑，其上层模型的优化目标往往仅选择为系统总走行时间最小，而没有考虑决策者的风险态度对于网络优化方案的影响，这与实际情况不符.因此，针对上层模型进行目标函数改进，使其反映决策者的决策行为，是网络优化问题的研究重点之一.

Yang等［1］对于网络优化问题的目标函数进行了总结，发现在双层规划模型中，通常将目标函数设定为系统总走行时间最小.Williams等［2］以出行者剩余最大化作为网络设计目标，建立了网络优化模型，并且分析了交通网络性能改善措施对于出行者消费剩余的影响.对于其他单目标优化问题，在上层模型中，决策者可以选用其他优化目标，如交通网络可靠性最大化［3］、网路使用时环境污染最小化［4］、交通网络公平性最大化［5］等.文献［6-7］建立了一种同时考虑系统总走行时间、网络建设成本等多个目标的交通网络优化模型并进行了求解.文献［8-10］研究了基于需求不确定的连续交通网络设计问题，以总走行时间的期望和标准差的算数加权平均值最小化作为上层模型的优化目标.

为了能够更好地描述现实问题，本文假定交通需求和交通供给是服从一定概率分布的随机变量，基于VaR理论建立了考虑决策者风险态度的不确定网络优化模型.随后，给出了求解该模型的算法，并使用实验网络对其进行了验证.

1 基于风险价值的不确定交通网络优化模型

1.1 风险价值理论

统计学和金融学中度量风险的经典指标有:①半方差和半标准差的风险度量;②均值-绝对偏差风险度量;③ 绝对偏差风险度量;④ 极大化极小策略的风险度量［11］.这些传统的基于偏离度的风险度量往往无法概括分布的特征以及小概率的事件.为了克服这一缺点，在风险管理的实践中，研究者们提出了基于风险价值理论的风险度量方法［12］.所谓风险价值就是在给定的置信水平下，发生不超过某一目标区域范围的预期最大亏损额度，即

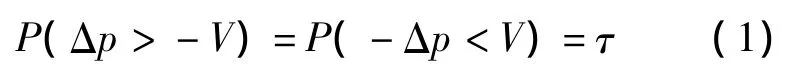
式中，Δp表示收益;－Δp表示亏损;V表示给定置信水平τ下的风险价值.由此可知，风险价值V描述了一种分布特征，该分布具有单调性、固定转换性、同质性和次加性.

给定网络设计中某个路段走行时间的风险价值为

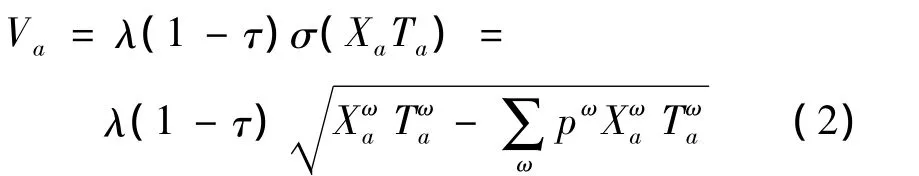
式中，Xa为路段a的路段交通流量，其均值为xa，标准差为σxa;λ为给定置信水平下的分位数;Ta为路段a的走行时间函数;ω∈Ω为任意一随机情景，对应的概率为pω.

对于整体网络来说，走行时间的标准差为

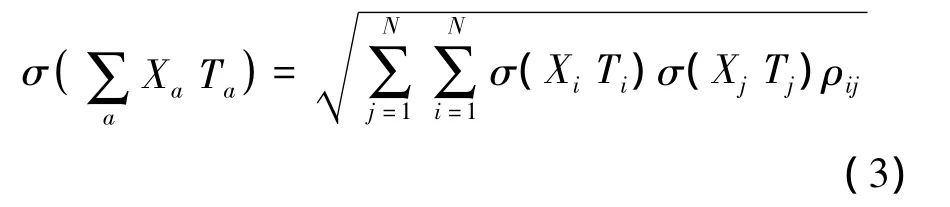
式中，ρij为2条路段走行时间的相关系数;Xi为路段i的路段交通流量，其均值为xi，标准差为σxi;Ti为路段i的走行时间函数.

网络的风险价值可表示为

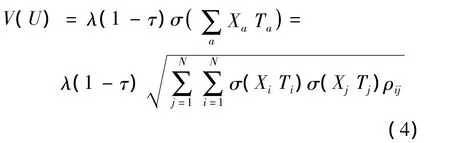
式中，U为由N条路段组成的网络.

当 ρij=0 时，有

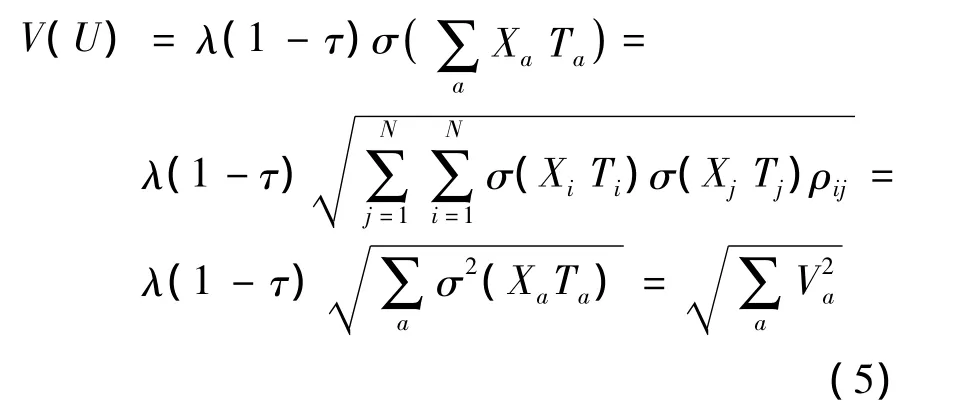
当 ρij=1 时，有

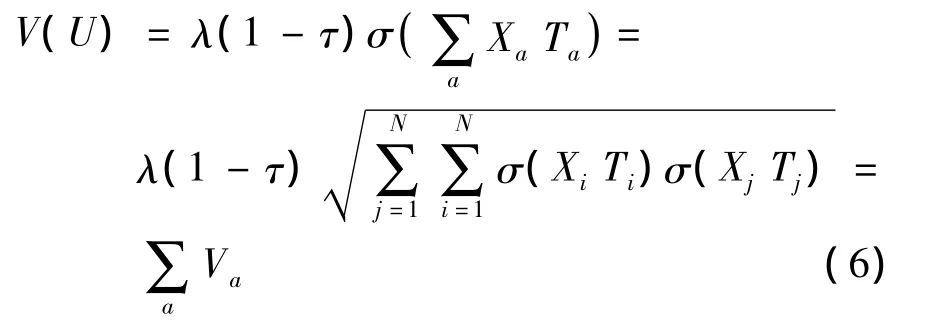
现实中不同路段走行时间不可能完全正相关，路径走行时间的波动性小于路段走行时间的波动性.为了计算的方便，以下分析中均假设ρij=0.

1.2 模型设计

1.2.1 多目标模型Ⅰ

假定路段通行能力和OD需求是服从一定概率分布的随机变量，建立基于风险价值的多目标网络设计模型Ⅰ.该模型为双层规划模型，上层模型为决策者决定新建或者扩建的路段集合，共包含2个目标函数:①系统总走行时间的均值最小;②系统总走行时间的风险价值最小.约束条件为建设资金投入小于预算资金.上层模型可表示为

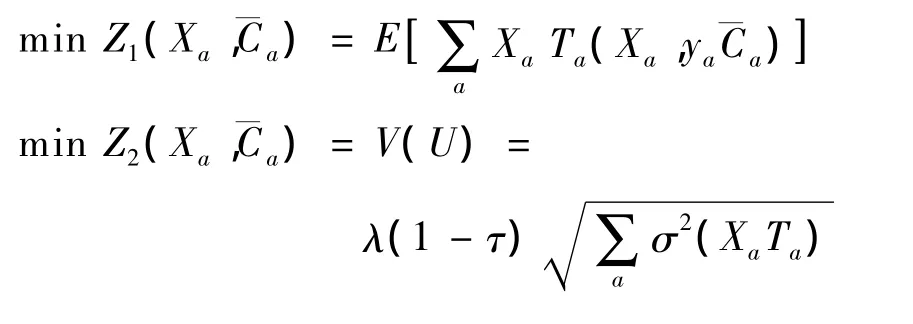
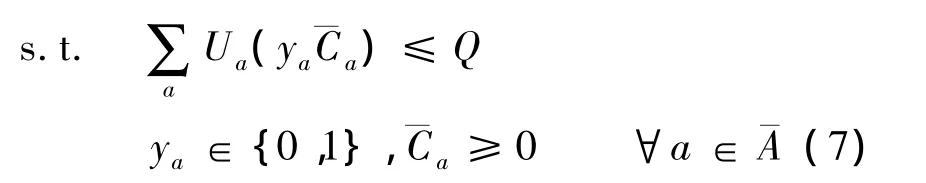
式中，Z为上层模型的目标函数;¯Ca为新建或者扩建路段新增的通行能力;Ua为新建或者扩建路段的投资成本函数;¯A为交通网络中新建或者扩建路段的集合;ya为决策变量，且ya=1表示新建路段，ya=0表示不建路段;Q为新建或者扩建路段的资金预算.

假设X=X(ya¯Ca)为ya的隐函数，由下层模型决定.下层模型为基于期望效用理论的均衡模型，可表示为

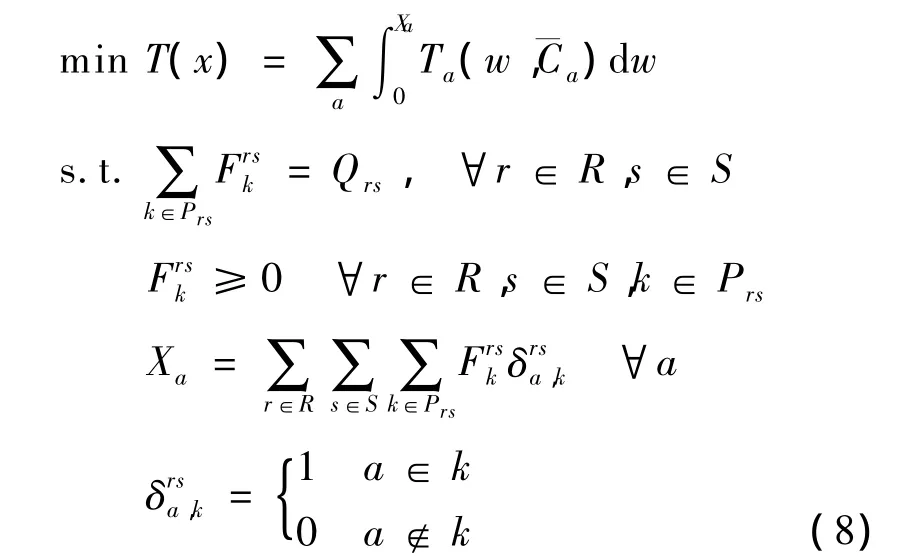
式中，T为下层模型的目标函数;R为交通网络中交通发生点的集合;r为任意一个交通发生点;S为交通网络中交通吸引点的集合;s为任意一个交通吸引点;Prs为OD对之间的路径集合;Qrs为OD对r，s之间的需求量，其均值为qrs，残差项为 εrs，标准差为为OD对r，s之间路径k的流量，其均值为frsk.

假设路段通行能力是独立的随机变量，则路径走行时间可以表示为

式中，ta0为路段a的自由流走行时间;Ca0为路段a的原有通行能力;α，β为路段通行时间函数的参数.Ca0，ya¯Ca分别服从于参数为 θa0，θa的均匀分布的随机变量.

路段建设投资函数Ua可表示为

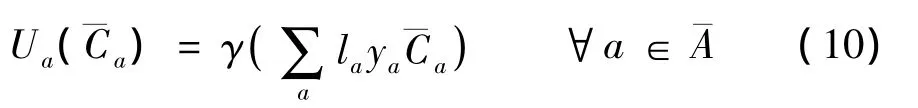
式中，la为新建或者扩建路段的长度;γ为单位长度路段单位通行能力新建或者扩建的成本.

上下层规划由决策变量ya和路段交通量Xa联系.

1.2.2 多目标模型Ⅱ

假定路段通行能力和OD需求是服从一定概率分布的随机变量，建立基于风险价值的多目标网络设计模型Ⅱ.其上层模型为决策者决定新建或者扩建的路段集合，共包含3个目标函数:①系统总走行时间的均值最小;② 系统总走行时间的风险价值最小;③ 网络总投资最小.下层模型为基于期望效用理论的均衡模型.模型Ⅱ可表示为

式(11)中的路段走行时间可用式(9)来表示，路段建设投资函数Ua可用式(10)来表示.

2 模型求解算法

为了解决基于VaR理论的多目标不确定交通网络设计模型问题，本文使用了基于蒙特卡洛模拟的遗传算法，其具体步骤如下.

1)初始化.

①设计遗传算法染色体的编码方案，确定优化问题的适应度函数.确定种群规模O、种群进化的最大代数T以及交叉概率和变异概率.

②根据预算约束生成初始种群P(0)，其中个体数量为O.同时设外部档案集合Q(0)为空，种群代数计数器t=1.

2)设种群个体计数器o=1，对给定的种群P(t)中的个体进行以下操作:

①根据染色体P(t)o的方案更新网络参数，设随机供给与需求抽样计数器y=1.

②进行供给和需求的随机抽样，根据抽样得到的参数进行下层模型的交通分配.

③根据下层模型的分配结果，计算上层模型的目标函数值.

④如果y＜Y，则返回步骤②，且y=y+1;否则，计算P(t)o对应的目标函数的值，进入步骤⑤.

⑤ 如果o＜O，则返回步骤①，且o=o+1;否则，t=t+1，进入步骤3).

3)如果t＜T，则执行改进的强度帕累托进化算法(SPEA2);否则，进入步骤4).

4)形成帕累托最优解，终止计算.

3 算例

3.1 参数设置

采用经典的Nguyen-Dupuis测试网络进行算例分析(见图1).该网络共有13个节点、19个路段和4个OD对.图中，A，D为交通需求发生点，B，C为交通需求吸引点，实线线段为已建成的现状路段，虚线线段为待建的路段.网络路段的基本信息列于表1，包括路段编号、起终点、自由流走行时间、现状和规划通行能力以及均匀分布的参数、新建或者扩建的预算建设成本.随机OD需求列于表2，本算例中假设随机OD服从截尾正态分布.

图1 Nguyen-Dupuis网络结构

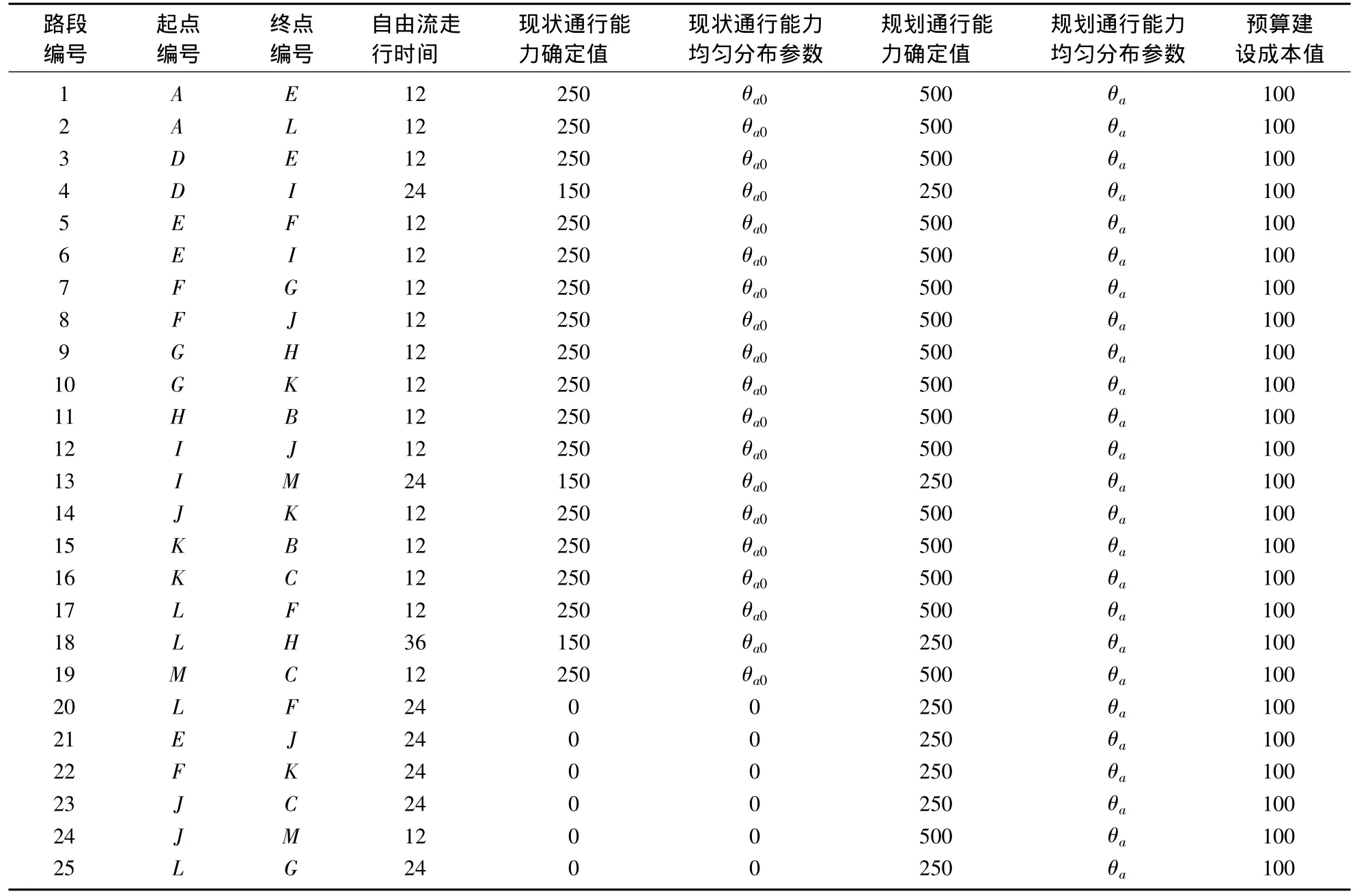
表1 Nguyen-Dupuis网络的基本属性

表2 OD交通需求的基本情况

3.2 计算分析

待建与扩建路段共25条，使用二进制编码方法，故染色体长度也为25.用1表示新建或者扩建的道路，0表示维持原状的道路，前6位数字表示新建道路，其余19位数字表示扩建道路，顺序依照路段编号次序.

情景A为多目标模型Ⅰ的不确定离散交通网络设计问题，其中用户类型为风险中性.遗传算法基本参数设置如下:进化终止代数为1 000，种群规模为50，代沟为 0.9，变异概率为 0.15，交叉概率为0.75，走行时间函数参数 α =0.15，β =4，其他参数详见表3.

图2为情景A的计算结果.由图可知，算法的收敛速度较好.此外，还可以得出:①系统总出行时间均值和风险价值具有反向关系.在预算约束和需求不确定程度相同的情况下，系统总走行时间越大，总走行时间的风险价值越小;系统总走行时间越小，总走行时间的风险价值越大.②在相同预算水平下，需求随机程度越大，有效前沿的点分布越分散.③ 置信水平越高，风险价值的数值越大，对于风险就更加厌恶.④当供给存在不确定性时，供给随机程度越大，相同风险水平下的总走行时间越大.⑤ 在相同的需求不确定程度下，预算水平增加，会造成帕累托有效前沿对应的系统总走行时间均值和风险价值下降.

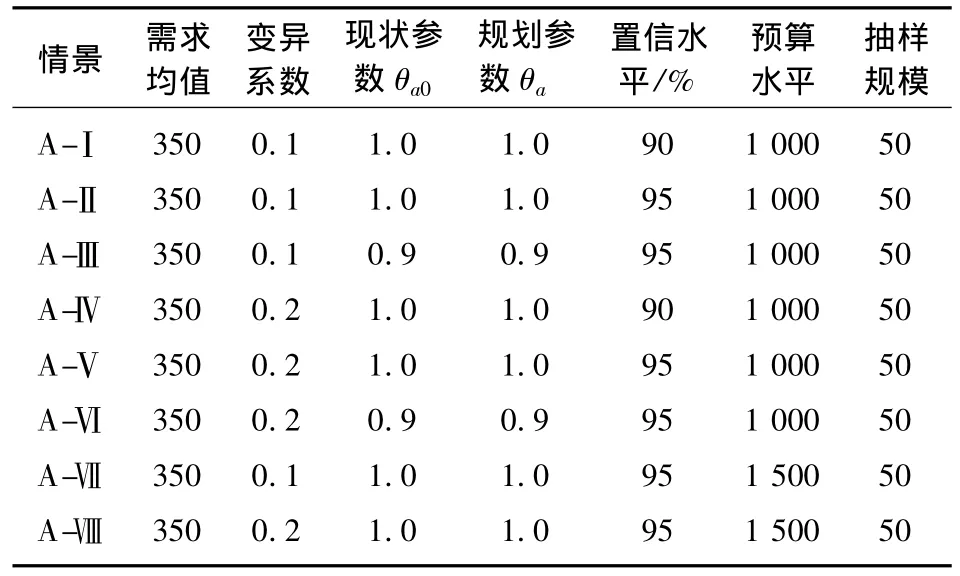
表3 情景A的基本参数

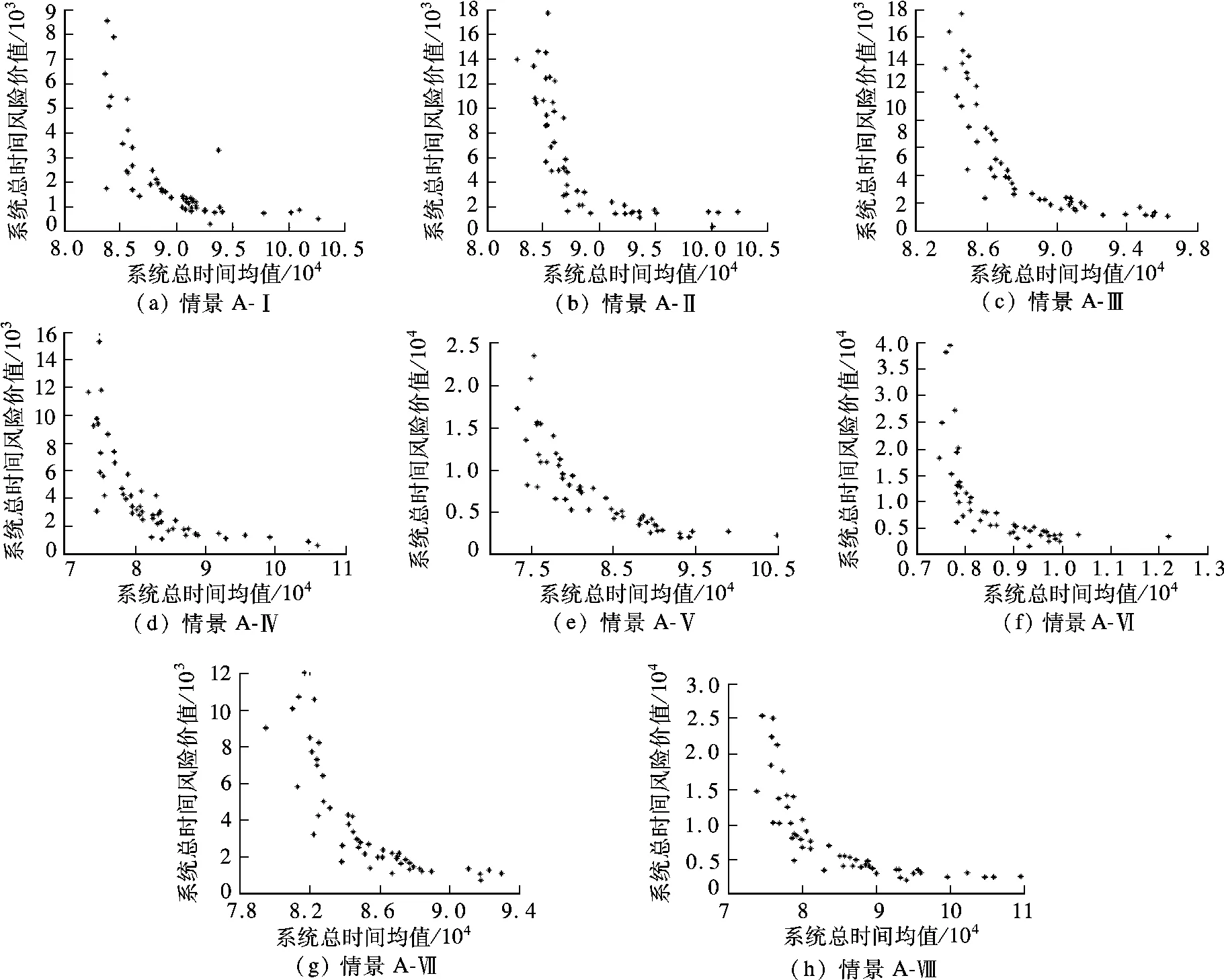
图2 情景A的计算结果

图3 情景B的计算结果

情景B为多目标模型Ⅱ的不确定离散交通网络设计问题，其中用户类型为风险中性.遗传算法基本参数设置为:进化终止代数为1 000，种群规模为100，代沟为 0.9，变异概率为 0.15，交叉概率为0.75.走行时间函数参数 α =0.15，β =4，需求均值为350，变异系数为0.2，现状通行能力与规划通行能力分布参数为1，置信水平为90%，供给与需求抽样规模为50.图3表示多目标模型Ⅱ种群进化到1 000代时的帕累托有效前沿，其沿3个坐标轴方向的投影如图4所示.由图可知，网络建设成本、网络系统总出行时间均值及系统总出行时间的风险价值三者之间存在替代关系.增加建设资金可以有效地提高网络性能，但是当投入资金增加到一定额度以后，改善的效果不明显.当建设资金投入接近0时，网络的性能变得不稳定.

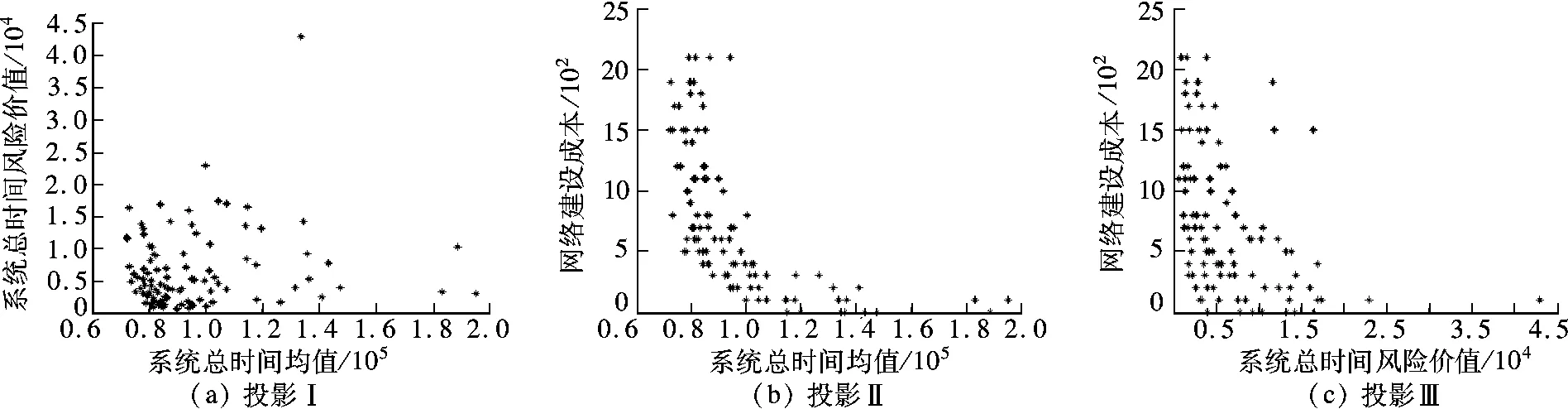
图4 情景B在3个坐标轴方向上的投影

4 结语

针对传统四阶段法中对于现实条件的不合理假设，通过假定交通供给和需求是概率分布给定的随机变量，基于VaR理论建立了一种考虑决策者风险态度的不确定多目标离散交通网络设计模型，并给出了基于遗传算法的求解方法.基于Nguyen-Dupuis网络的计算结果表明:风险价值可以有效地度量决策者的风险态度;网络建设成本、网络系统总出行时间均值、系统总出行时间的风险价值三者之间存在替代关系;增加建设资金可以有效地提高网络性能，但是当投入资金增加到一定额度以后，改善的效果不明显.下一步的研究主要集中在分析参数的选择对于网络优化结果的影响上，以便更好地将VaR应用于规划实践.

［1］Yang H，Bell M G H.Models and algorithms for road network design:a review and some new developments［J］.Transport Reviews，1998，18(3):257-278.

［2］Williams H C W L，Lam W M.Transport policy appraisal with equilibrium modelsⅠ:generalized traffic and highway investment benefits［J］.Transportation Research Part B:Methodological，1991，25(5):253-279.

［3］许良，高自友.基于连通可靠性的城市道路交通离散网络设计问题［J］.燕山大学学报，2007，31(2):159-163.

Xu Ling，Gao Ziyou.Urban road transportation discrete network design based on connectivity reliability［J］.Journal of Yanshan University，2007，31(2):159-163.(in Chinese)

［4］刘娟娟，范炳全，祝炳发.双层规划在城市交通污染控制中的一个应用［J］.管理工程学报，2005，19(4):87-90.

Liu Juanjuan，Fan Bingquan，Zhu Bingfa.An apply of bi-level programming in the urban transport pollution control［J］.Journal of Industrial Engineering and Engineering Management，2005，19(4):87-90.(in Chinese)

［5］ Meng Q，Yang H.Benefit distribution and equity in road network design［J］.Transportation Research Part B:Methodological，2002，36(1):19-35.

［6］ Friesz T L，Mehta N J，Nam K，et al.The multi-objective equilibrium network design problem revisited:a simulated annealing approach［J］.European Journal of Operational Research，1993，65(1):44-57.

［7］Tzeng G H，Tsaur S H.Application of multiple criteria decision making for network improvement plan model［J］.Journal of Advanced Transportation，1997，31(1):48-74.

［8］Ukkusui S V，Mathew T V，Waller S T.Robust transportation network design under demand uncertainty［J］.Computer-Aided Civil and Infrastructure Engineering，2007，22(1):6-18.

［9］ Karoonsoontawong A，Waller S T.Robust dynamic continuous network design problem ［J］.Transportation Research Record，2007，2029:58-71.

［10］Yin Y，Madanat S M，Lu X Y.Robust improvement schemes for road networks under demand uncertainty［J］.European Journal of Operational Research，2008，198(2):470-479.

［11］马孝先.金融优化与风险度量［M］.北京:中国财政经济出版社，2009.

［12］ Philippe Jorion.Value at risk:the benchmark for controlling market risk［M］.New York:Irwin Professional Publishing，1996.

Discrete traffic network design model under supply and demand uncertainty

Lu Huapu1Li Yue1Yu Xinxin2

(1Institute of Transportation Engineering，Tsinghua University，Beijing 100084，China)
(2Transport Planning and Research Institute of Ministry of Transport，Beijing 100028，China)

Regarding the uncertainty of traffic supply，demand and decision principles in traffic design，a design model for uncertain discrete traffic network based on uncertainty theory is proposed.Firstly，supply and demand elements are assumed to be stochastic variables.The semi-standard error and value at risk are used to measure uncertainty and a multi-objective bi-level optimized model considering decision risk attitude is built.Then，SPEA2(strength pareto evolutionary algorithm 2)based on the conception of Pareto is applied to solve the multi-objective bi-level optimized model.The numerical results of Nguyen-Dupuis network show that the risk value can reflect decision maker's attitude towards risk in measuring traffic design.In various targets there are alternative relations in multi-object design.The increase of the construction funds can effectively improve the network performance.However，such improvement is not obvious when the investment is beyond a certain limit.

discrete traffic network design;supply and demand uncertainty;risk attitude;value at risk;bi-level optimization

U491.1

A

1001－0505(2012)06-1221-06

10.3969/j.issn.1001 －0505.2012.06.036

2012-02-26.

陆化普(1957—)，男，博士，教授，博士生导师，luhp@mail.tsinghua.edu.cn.

国家高技术研究发展计划(863计划)资助项目(2007AA11Z202，2007AA11Z233)、教育部博士点基金资助项目(20070003065).

陆化普，李悦，蔚欣欣.供给与需求不确定的离散交通网络设计模型［J］.东南大学学报:自然科学版，2012，42(6):1221-1226.［doi:10.3969/j.issn.1001 －0505.2012.06.036］