一种计算混合过程尺度变化的新方法
骆培成 辛传贤 曹翠翠 赵素青 周建成
(东南大学化学化工学院,南京 211189)
一种计算混合过程尺度变化的新方法
骆培成 辛传贤 曹翠翠 赵素青 周建成
(东南大学化学化工学院,南京 211189)
基于混合区域内子区域之间接触面的性质,提出了一种计算混合过程尺度指数和离析尺度的新方法.尺度指数可以定量表征混合过程中微团的尺度变化,反映了混合体系中微团离析尺度与计算尺度的差异.在一定的计算尺度下,当两组分(或两相)微团互不接触时,尺度指数为1;当两组分(或两相)微团最大限度相互接触时,体系具有最小尺度指数0.对于特定的混合状态,计算尺度对离析指数的影响较大,在实际应用中计算尺度应小于体系内微团的最小尺度.根据一定计算尺度下尺度指数的计算结果,可以计算出特定混合状态下的离析尺度.离析尺度可以表征混合区域内相互离析的两组分(或两相)微团的尺度大小,反映了混合过程尺度降低的程度.
混合;尺度变化;定义;尺度指数;离析尺度
混合是化工生产过程中重要的单元操作,其目的是降低系统的不均匀程度.例如,通过均相湍流混合或者层流混合,可降低系统在浓度、温度等标量上的不均匀程度;通过非均相混合过程(如气相在液相中的分散等),可降低两相之间的相互分散程度[1].如何科学、定量地描述这种不均匀程度,即利用特定的参数对混合过程的状态进行数学描述,使其与客观混合状态之间建立科学的联系,是混合过程研究领域中的难点之一.
早在20世纪50年代,Danckwerts[2]就提出了离析强度和离析尺度的概念,并基于混合区域内的浓度分布方差来计算离析强度,表征混合过程的状态.时至今日,该方法仍被广泛应用于混合过程研究中[3-6].然而,该方法不能用于评价混合过程的尺度降低情况.离析尺度是指体系中某一组分(或者某一相,以下统一用组分来表示)形成的相对孤立的微团尺寸,与该组分微团相邻的区域为其他组分微团.目前,计算混合过程离析尺度的方法主要有相关曲线图法[2,7]、条纹宽度法[8-11]、最近相邻点分布法(PNN 法)[9-10]、变量图法[12-13]等.Kukukova等[14]详细比较了这4种方法在计算体系离析尺度方面的适用情况以及方法的优缺点.
本文提出了一种新的计算混合过程中尺度变化的方法.基于混合区域内各子区域之间相互接触面的性质,定量计算出混合区域的尺度指数和离析尺度.此处提出的尺度指数概念,是从尺度变化的角度定量描述混合过程的进度;离析尺度则反映了混合区域内孤立微团的空间尺寸.
1 混合区域描述及相关尺度定义
图1为混合过程中不同阶段两组分微团相互分散示意图.假设混合区域由n2个大小相等的正方形子区域组成,每个子区域的大小为L×L,混合区域的大小为nL×nL.本文主要考虑混合过程中的尺度变化,并不考虑每个子区域在浓度或者温度上的变化.因此,最小子区域内只可能存在A组分微团或者B组分微团.用1表示该子区域为A组分微团(图1中黑色区域),0表示该子区域为B组分微团(图1中白色区域).
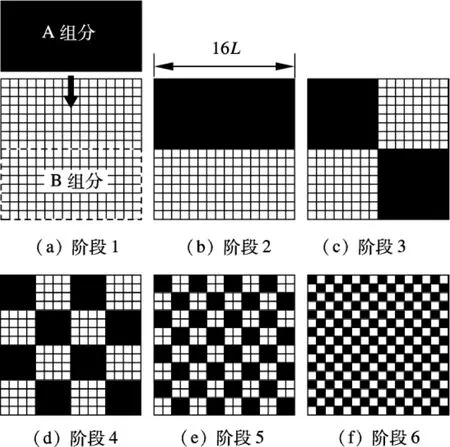
图1 混合过程不同阶段两组分微团相互分散示意图
用正方形区域的边长表示该区域的尺度,则图1中整个混合区域的尺度为nL,最小子区域的尺度为L.对于只有A组分或者只有B组分的孤立微团(即该微团周围均为其他组分微团),定义微团的离析尺度Ls为

式中,S表示微团所占区域的面积;mL表示与微团具有相同面积的正方形区域的边长,即最小尺度L的m倍.
在计算尺度指数和离析尺度时,需将整个混合区域划分为若干个大小相等的正方形子区域.该子区域对应的尺度为计算尺度Lc,一般采用混合区域的最小尺度L进行计算.在实际应用中,对于由各种实验手段得到的混合过程浓度分布图或者不互溶两相之间的分散图,可以取图像中一个像素对应的尺度作为计算尺度.
2 尺度指数与离析尺度的计算方法
2.1 尺度指数
在最小尺度下,整个混合区域被分成n2个子区域.相邻2个子区域之间存在1个界面.如果界面两侧为同一组分微团,则说明该界面属于微团内部界面;如果界面两侧为不同组分微团,则说明该界面为组分间界面.统计计算区域内的所有界面,内部界面所占总界面的比例即为尺度指数Is.当计算尺度Lc=L时,混合区域内的总界面数Ftot为

如图1(a)所示,当计算尺度为L时,在混合过程的初始阶段,A组分微团与B组分微团互不接触,尺度指数Is=1,表示两组分微团完全离析,且它们均为具有最大尺度的微团.随着混合过程的进行,A组分微团和B组分微团之间的接触界面越来越大(见图1(b)~(f)).当A组分微团和B组分微团均达到最小微团尺度(见1(f))时,混合区域内两组分微团具有在该计算尺度下的最大接触面积,此时A组分微团和B组分微团相互均匀分散,尺度指数Is=0.定义每条界面处的性质参数为β,且当界面两侧区域微团组分相同时β=1,否则β=0.则在该计算尺度下,整个区域的尺度指数Is为

单独考虑A组分微团时,假设在整个混合区域内,其浓度为xA.所有A组分微团组成一个微团,具有最大尺度指数(→1),此时微团内的界面数近似等于2n(n-1)xA(n≫1).假设在计算区域内,界面两侧均为A组分微团的界面总数为FA,则A组分微团的尺度指数Is,A为
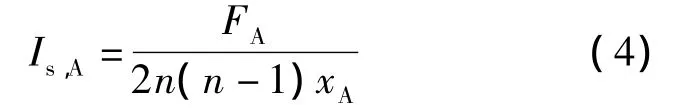
相应地,假设界面两侧均为B组分微团的界面数为FB,则B组分微团的尺度指数Is,B为
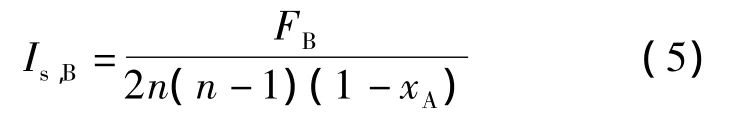
2.2 离析尺度
在实际应用中,混合区域内的微团往往具有不规则的形状,本文通过计算微团的离析尺度来考察混合区域内A,B两组分微团的混合状态.当计算尺度Lc=L时,根据式(3)可计算得到A,B两组分微团的平均尺度指数为Is.假设在该混合状态下,A,B两组分微团的平均离析尺度为mABL.分别以mABL和L作为计算尺度,得到混合区域内的界面总数存在如下关系:

根据式(6)便可计算出混合区域中两组分微团的平均离析尺度Ls,AB,即

此外,可以根据式(4)和(5)计算得到的单组分微团的尺度指数,单独计算A组分微团的离析尺度(mAL)和B组分微团的离析尺度(mBL).对于A组分微团,有

B组分微团的离析尺度Ls,B为

3 结果与讨论
3.1 尺度变化的定量表征
在混合开始前,混合区域内只有B组分微团(见图1(a)),此时A组分微团和B组分微团完全离析.随着混合过程的进行,体系中A组分微团和B组分微团的尺度不断降低,最终在最小尺度L下,A组分微团和B组分微团完全分散(见图1(f)).
在混合过程中,假设离析尺度每次都减小为上一离析尺度的1/2.微团的离析尺度从最初的nL降低至mL所需的次数为“混合时间”τm,则

将混合的初始阶段记为混合的零时刻,混合体系的离析尺度为nL.由τm的定义可知,由图1(a)所示的混合初始阶段至图1(b)~(f)所示的混合阶段所需时间分别为 0.5,1,2,3,4.在不同的计算尺度下,图1所示的各个混合阶段对应的尺度指数与τm的关系如图2所示.
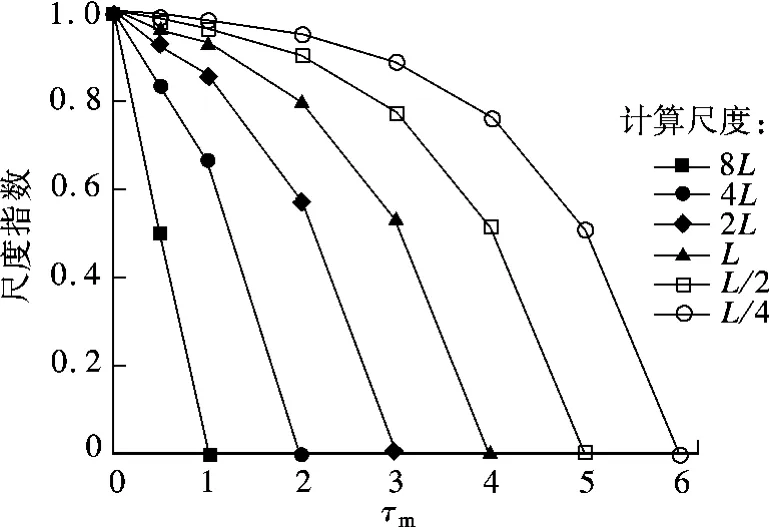
图2 不同计算尺度下尺度指数与混合时间的关系图
由图2可知,随着混合时间τm的不断增加,混合区域的尺度指数由最初的1降低到最终的0,尺度指数的降低反映了混合过程中离析尺度由大至小不断降低的过程.因此,可以利用本文提出的尺度指数概念来定量描述混合过程中混合区域内A,B两组分微团相互分散的程度.当尺度指数为0时,A,B两组分微团相互分散程度达到最大,且都具有最小微团尺度;当尺度指数为1时,两组分微团互不接触,且都具有最大微团尺度.
3.2 计算尺度的影响
从图2可以看出,在混合的初始阶段(即微团尺度与计算尺度相差较大时),系统的尺度指数随混合时间变化的速率(即图2中曲线的斜率)相对较小.混合区域内微团尺度越接近计算尺度,尺度指数随混合时间变化的速率越快.这主要是因为本文提出的尺度指数是基于A,B组分所组成的微团的界面性质来进行计算的.当体系中微团的尺度越接近计算尺度时,两组分微团越容易接近最终的混合状态.
由图2可知,在任何计算尺度下,当体系中的微团尺度与计算尺度相等时,混合区域的尺度指数为0.对于图1(d)所示的混合状态,体系中的微团尺度为4L.以4L作为计算尺度时,该混合状态对应的尺度指数为0;而以L作为计算尺度时,此混合状态对应的尺度指数为0.8,若将计算尺度进一步降低,如降低至L/4,则混合状态对应的尺度指数为0.95.这意味着,与计算尺度L/4相比,图1(d)中的微团尺度(4L)远大于计算尺度.因此,在该计算尺度下,混合体系仍具有较高的尺度指数.这也表明尺度指数代表了体系中相互离析的微团尺度与计算尺度的差异.尺度指数越大,体系中的微团尺度与计算尺度的偏差越大;尺度指数越小,微团的离析尺度与计算尺度越接近.
相反地,当体系中的微团尺度小于计算尺度时,如图1(e)所示的混合状态,体系内的微团尺度为2L.若以4L为计算尺度,则在每一个4L×4L区域内既有A组分微团又有B组分微团,用于计算的子区域不属于单组分微团,无法根据本文定义计算体系的尺度指数.因此,利用本文提出的概念表征体系的尺度变化时,针对特定的混合状态,需要选择合适的计算尺度来计算尺度指数.一般来说,计算尺度要小于体系内单组分微团的最小尺度.若体系中大部分微团的尺度都小于计算尺度,则说明在此计算尺度下,体系已经达到较好的混合状态,如要进一步评价体系的混合状态,需要选择更小的计算尺度来进行计算.
3.3 离析尺度的计算分析
利用本文提出的尺度指数概念,可以定量地评价混合区域内A,B两组分微团的相互分散状态.然而,在实际应用中,混合区域内的微团往往具有不规则的形状.在图3所示的各个混合状态中,混合区域大小均为256L×256L,A组分微团(黑色区域)所占的面积分数xA也均为0.5.图3(a)~(d)中的A组分微团为圆形,数量分别为1,4,16,127,圆形微团的直径分别为204L,102L,51L,18L;图3(e)和(f)中A组分微团则呈不规则形状.

图3 不同形状的A组分微团在B组分微团中的分散示意图
以L为计算尺度,分别利用式(3)~(5)计算各混合状态下的平均尺度指数、A组分微团尺度指数和B组分微团尺度指数,计算结果见表1.由表可知,对于混合状态1~4,尺度指数不断降低,表明混合过程中微团尺度不断降低.
根据在计算尺度L下获得的尺度指数,利用式(7)~(9)分别计算图3中各种混合状态对应的A,B两组分微团的平均离析尺度、A组分微团离析尺度和B组分微团离析尺度,计算结果见表1.由表可知,根据尺度指数计算得到的A组分微团离析尺度与混合区域内A组分微团的实际尺度(这里用与A组分微团实际面积相等的正方形的边长m'L表示)相接近.对于图3(c)所示的微团,其离析尺度为 39.4L,实际尺度为 45.3L.可以看出,计算得到的离析尺度略小于实际尺度,这主要是由于本文提出的尺度指数是基于A,B组分微团之间的接触面性质来进行计算的.实际上,A组分微团的最外层是与B组分微团相互接触的,在计算尺度指数时这部分属于微团间的界面,而不属于A组分微团内的界面,因此计算所得到的离析尺度理论上应小于其实际尺度.

表1 各种混合状态对应的尺度指数及离析尺度(Lc=L)
同一混合状态下计算得到的A,B组分微团的离析尺度差异较大.对于混合状态1,计算得到的A,B两组分微团的离析尺度分别为159.1L和70.9L,即B组分微团的离析尺度远小于A组分微团;事实上,从图3(a)可以看出,A,B两组分微团内任意点至A,B组分接触界面的最大距离分别为79L和102L.计算得到的A,B微团离析尺度的差异客观地反映了混合区域内单组分微团内部离两组分接触界面远近的差异.也就是说,离析尺度越大,则微团内部离两组分接触界面的距离越大,该微团内部的某些部分越不容易达到两组分接触界面,混合过程越不容易实现.
另外,虽然图3(a)和(e)中的微团均为连续性微团,但是图3(e)中两组分微团的混合状态5优于图3(a)中的混合状态1.由表1可知,在混合状态1,5下 A组分微团的离析尺度分别为159.8L和89.8L,与实际混合状态相符.混合状态5下A组分微团的离析尺度与混合状态2下A组分微团的离析尺度(80.2L)相近,说明这2种混合状态较接近.混合状态6下A组分微团和B组分微团的离析尺度分别为12.6L和11.9L,与混合状态4下两组分微团的离析尺度较为接近,表明这2种混合状态较为接近,这与图3所示的实际混合状态相吻合.
综上所述,本文提出的离析尺度计算方法能够科学地描述两组分微团的混合状态.在现有的微团离析尺度计算方法中,PNN法[9-10]只适用于尺寸均一的不溶颗粒物在分散介质中的分散过程,因此不能利用该方法计算图3(e)和(f)中微团的离析尺度.条纹宽度法[8-11]根据混合区域内某条截线上条纹宽度的分布来计算混合过程的离析尺度,因此,截线位置的选择对离析尺度的计算结果具有重要的影响,如对于图3(b)所示的混合状态2,当截线处于中心线位置时,A组分微团和B组分微团的离析尺度分别为54L和159L;当截线由中心线位置向上平行移动64L后,A组分微团和B组分微团的离析尺度分别为100L和30L.相关曲线图法[2]是通过分析某一混合区域内处于不同距离两点间的浓度相关系数与该距离大小的图谱特性,间接计算体系的离析尺度.利用该方法进行计算时存在一定的限制条件,即不能对混合状态较差(如图3(e)所示的混合状态5)和混合区域呈周期性变化规律(如图3(d)所示的混合状态4)的离析尺度进行计算.利用该方法对图3(f)所示的混合状态6进行计算时,得到的混合区域平均离析尺度为3.2L,与该混合区域的实际微团尺度偏差较大.变量图法和相关曲线图法[12-13]的计算原理类似,两者的定义都较为抽象,计算过程复杂,因此在实际中应用较为困难.
4 结语
离析强度和离析尺度是用于定量评价混合过程所达到程度的2个重要参数.本文基于混合区域内子区域之间接触面的性质,提出了一种计算混合过程尺度变化的新方法.该方法可以定量地表征不同组分或者不同相在混合过程中由于尺度的变化对混合过程进度的影响,进而提出了尺度指数的概念.对于特定的混合状态,系统的尺度指数与所选取的计算尺度相关,体系中微团的尺度与计算尺度偏差越大,尺度指数越接近于1.利用在一定计算尺度下尺度指数的计算结果,可以计算出特定混合状态下混合区域的平均离析尺度和单组分的离析尺度.离析尺度可以有效表征混合区域内独立微团的尺度大小,计算结果与微团的实际尺寸吻合较好.
[1] Paul E L.Handbook of industrial mixing:science and practice[M].New York:John Wiley & Sons,Inc.,2004.
[2] Danckwerts P V.The definition and measurement of some characteristics of mixtures[J].Applied Scientific Research,1952,3(4):279-296.
[3] Unger D R,Muzzio F J.Laser-induced fluorescence technique for the quantification of mixing in impinging jets[J].AIChE Journal,1999,45(12):2477-2486.
[4]Luo P C,Cheng Y,Jin Y,et al.Fast liquid mixing by cross-flow impingement in millimeter channels [J].Chemical Engineering Science,2007,62(22):6178-6190.
[5]Liu Z,Cheng Y,Jin Y.Fast liquid jet mixing in millimeter channels with various multislits designs[J].Industrial&Engineering Chemistry Research,2008,47(23):9744-9753.
[6]Kukukova A,Aubin J,Kresta S M.A new definition of mixing and segregation:three dimensions ofa key process variable[J].Chemical Engineering Research&Design,2009,87(4A):633-647.
[7]Lacey P M C,Mirza F.Study of structure of imperfect mixtures of particles[J].Powder Technology,1976,14(1):25-33.
[8]Mohr W D,Saxton R L,Jepson C H.Mixing in laminar-flow systems[J].Industrial&Engineering Chemistry,1957,49(11):1855-1856.
[9]Aubin J,Fletcher D F,Xuereb C.Design of micromixers using CFD modeling[J].Chemical Engineering Science,2005,60(8/9):2503-2516.
[10] Kukukova A,Noel B,Kresta S M,et al.Impact of sampling method and scale on the measurement of mixing and the coefficient of variance[J].AIChE Journal,2008,54(12):3068-3083.
[11] Bothe D,Stemich C,Warnecke H J.Computation of scales and quality of mixing in a T-shaped microreactor[J].Computers&Chemical Engineering,2008,32(1/2):108-114.
[12]Gullett B K,Groff P W,Stefanski L A.Mixing quantification by visual imaging analysis[J].Experiments in Fluids,1993,15(6):443-451.
[13]Carle S F,Fogg G E.Transition probability-based indicator geostatistics[J].Mathematical Geology,1996,28(4):453-476.
[14] Kukukova A,Aubin J,Kresta S M.Measuring the scale of segregation in mixing data[J].Canadian Journal of Chemical Engineering,2011,89(5):1122-1138.
A new method for determining scale changes in mixing process
Luo Peicheng Xin Chuanxian Cao Cuicui Zhao Suqing Zhou Jiancheng
(School of Chemistry and Chemical Engineering,Southeast University,Nanjing 211189,China)
A new method is proposed to calculate index of scale and scale of segregation of the segregated clusters in the mixing process based on the characteristics of the interfacial face between two neighboring sub-zones.Index of scale is used to evaluate the scale changes of the segregated clusters quantitatively in the mixing process,which indicates the differences between the scale of segregation and the calculating scale.At a given calculating scale,the value of the index of scale is 1 when the clusters of two components(or two phases)segregate from each other completely,and the value becomes 0 when the clusters have the maximum interfacial face.For a certain mixing state,the calculating scale has great effect on the value of index of segregation.In the application,the suggested calculating scale should be smaller than the minimum scale of the segregated clusters in the mixing region.The scale of segregation can be determined by the value of index of scale calculated at a given calculating scale.The calculated scale of segregation reveals the actual size of the segregated clusters of the two components(or two phases)in the mixing zone.It can be used to evaluate the extent to which the scale reductions of the mixing process reach.
mixing;scale change;definition;index of scale;scale of segregation
TQ028.8
A
1001-0505(2012)06-1238-05
10.3969/j.issn.1001 -0505.2012.06.039
2012-06-23.
骆培成(1977—),男,博士,副教授,博士生导师,luopeicheng@seu.edu.cn.
国家自然科学基金资助项目(21006011)、江苏省自然科学基金资助项目(BK2010410).
骆培成,辛传贤,曹翠翠,等.一种计算混合过程尺度变化的新方法[J].东南大学学报:自然科学版,2012,42(6):1238-1242.[doi:10.3969/j.issn.1001 -0505.2012.06.039]

