引入央行干预的汇率决定混沌模型构建

孙 倩

（1.湖南城市学院商学院，湖南 益阳 413002；2.中南大学 商学院，湖南 长沙 410082）

一 引言

20 世纪下半叶以来，由于自然现象和社会现象的复杂性，使得对动力学规律的描述一般不能通过线性动力学方程进行，而只能用非线性动力学方程进行描述，因此非线性科学得到蓬勃发展。一般情况下，非线性动力学方程不存在解析解。同时，人们发现一个由确定的非线性演化方程描述的系统，在远离平衡的情况下，当系统参数变化时，可能经过分岔而进入时空有序且对称性更低的耗散结构状态或更为无序的混沌状态。但是这种混沌状态并不像噪声那样是一种完全无序的状态，而是混乱中有规律，但又是不具备明显对称特性的一种“序”。混沌的发现是20 世纪继相对论和量子力学之后物理学中最伟大的发现之一，它开创了科学模型化的一个新范例，为我们认识物质世界和人类社会的运动发展规律提供了新的思想和方法。80 年代，混沌理论开始向其他学科渗透，现在几乎遍及所有的自然科学和社会科学研究领域。基于混沌分析方法研究汇率决定理论就是在这种背景下产生的又一新的思路。

长期以来，汇率决定理论都是通过对相对货币供应量、利率、物价水平、经济增长、内外资产的替代性和均衡价格的调整速度等宏观影响因素的分析来解释汇率的决定和波动，并由此形成了以商品贸易为主的流量模型和以资产交换为主的存量模型。这些模型都基于同一前提条件：其涉及的各种经济变量都是可以计量的，因此其分析方法都是采用同一范式，因此上述模型建立的经济系统都具有确定性和决定性[1]。然而现实经济中，国际汇率的走势往往具有较大的随机性和不可预测性，尤其是自1973 年布雷顿森林体系解体后，国际金融领域发生了深刻变化，突出表现之一就是汇率的波动幅度空前加大，变动异常频繁，非线形特征更加明显。传统结构模型受线形条件约束，难以很好地解释非线性波动的汇率变量，也很难利用模型得出确定性的预测结果，大量的实证检验也表明，传统汇率理论的解释能力十分有限，尤其对短期内的汇率变化，预测能力甚至连简单的随机游走模型都不如。面对这一困惑，20 世纪80 年代以来很多学者不断寻求对传统理论的突破，开始尝试研究汇率决定和波动的非线性成因及其应用。以比利时经济学家保罗·德格劳威（Paul De Grauwe）为代表的一些学者受混沌理论的启发，认为汇率变化也是一个混沌过程，他们放弃了传统汇率理论理性预期的假设前提，代之以市场参与者异质性的假定，并试图通过混沌理论来模拟汇率的波动，从而开辟了汇率决定的混沌分析方法[2]。

1990 年，保罗·德格劳威（Paul De Grauwe）和汉斯·杜瓦赫特（Hans Dewachter）最早将混沌理论应用于汇率行为研究，他们开创性地提出了一个汇率决定的混沌模型。这个模型尽管简单，但是它说明了：如果假定代理人具有异质性，一个简单的非线性汇率决定模型描述的汇率行为可以变得相当复杂，在某些参数组合下，其波动甚至可以是混沌的。这一研究结果合理解释了很多传统汇率决定理论所无法解释的汇率现象。模型对初始条件的敏感性解释了国际金融外汇市场上均衡汇率的细微波动导致汇率时间路径的大相径庭；混沌系统的内在随机性波动，可用来阐释汇率决定的新闻模型无法解释在没有新闻发生时汇率的明显波动这一困惑。该模型的缺点是简单的把决定汇率的基本经济变量的结构当作是外生的，从而割裂了汇率与基本经济变量之间明显存在的相互联系[3]。为了克服这一缺陷，保罗·德格劳威等扩展了汇率决定混沌模型，提出了汇率决定的混沌货币模型。长期以来，通过对外汇市场进行实证检验，得出了两个被普遍认可的结论：汇率的时间序列呈现出单位根和远期升水是一个有偏的估计。扩展的汇率决定混沌货币模型不仅证明了在一定参数组合下，汇率波动能够呈现混沌状态，而且模型所描述的汇率波动具有实际汇率波动同样的特征，这在一定程度上也说明了汇率决定混沌货币模型的合理性。当然，现实的经济系统是一个相当复杂的非线性系统，从混沌理论的角度来研究汇率变动也面临一系列的问题。其中一个比较关键的问题就是，忽视了外汇市场中具有重要影响的中央银行干预这一关键因素，因此汇率决定混沌模型仍需要进一步的突破[4]。

二 传统汇率决定混沌模型回顾

（一）基本的汇率决定混沌模型

保罗·德格劳威和汉斯·杜瓦赫特最早给出的基本汇率决定混沌模型利用系统的观点将基于基本因素分析汇率决定的长期模型与基于非线性理论分析汇率决定的短期模型融为一体，认为市场对未来汇率变化的预期是两类投机者（技术分析者和基础分析者）对未来汇率的预期之和。

Ect（St+1）和Eft（St+1）分别代表技术分析者的预期汇率和基础分析者的预期汇率；mt是t 时期给予技术分析者预期汇率的权数，1-mt则是给予基础分析者预期汇率的权数。

权数mt定义为：

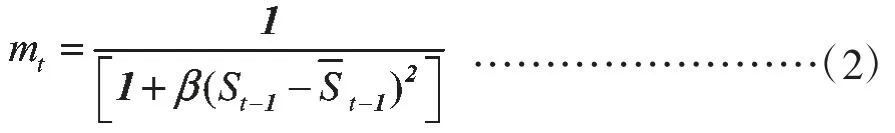
新闻模型构建的汇率决定模型为：

模型假定技术分析者用平均移动模型来预测汇率的未来走势，同时假定外生经济变量Xt=1，将（1）式和（2）式代入（3）式，从而得到一个简单的汇率决定混沌模型：

其中α 为基础分析者认为预期汇率回归均衡汇率的速度；γ 为技术分析者用历史数据推断未来汇率的因子[5]。从上述表达式可以看出，模型能否产生混沌，主要取决于技术分析者的外推参数和基础分析者预测未来汇率回归均衡汇率的速度参数α。当γ 越大或α 越小时，则模型获得混沌解的可能性越大[6]。

（二）扩展的汇率决定混沌模型

考虑到基本汇率决定混沌模型存在着割裂了汇率与基本经济变量之间联系的缺陷，保罗·德格劳威（Paul De Grauwe）等改进了基本模型，提出了一个相对完整的扩展汇率决定混沌模型。扩展模型保留了基本模型关于投机者预期异质的假定，通过融入多恩布什的粘性价格模型来考虑基本经济变量的现实结构。模型具体表述如下：

货币市场均衡：

开放的利率平价：

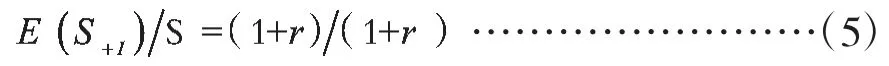
商品市场均衡：

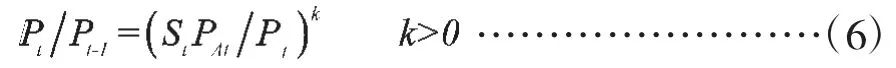
长期购买力平价：

式中Mdt、Mst、Yt、Pt、rt分别表示t 时期本国的货币需求量、货币供给量、总产出水平、价格水平和利率水平；rAt和PAt分别表示t 时期外国的利率水平和物价水平，和分别表示t 时期本国的均衡汇率水平、物价水平和外国均衡的物价水平；常数θ代表货币需求的收入弹性，λ 代表货币需求的利率弹性；k＞0 表征商品市场价格调整速度。

扩展模型假定经济处于充分就业状态，货币供给量和总产出水平都为外生变量，同时假定rAt=0，PAt=1，可以得出与式（3）对应的扩展的汇率决定模型：

将式（4）（5）（6）（7）代入式（8），再将其代入简单的汇率决定混沌模型，可以得到扩展的汇率决定混沌模型：

三 汇率决定混沌模型的改进

自1973 年布雷顿森林体系解体以来，西方主要工业化国家开始纷纷实行浮动汇率制，汇率波动剧烈，汇率在短期内的过分波动会降低它作为相对价格所发挥的引导资源合理流动的功能，对经济的稳定运行造成不利影响。因此中央银行外汇干预已成为政府调节宏观经济活动的重要手段和影响外汇市场供求的重要变量，是众多国家的一项重要经济政策。无论选择何种汇率制度，单独浮动、钉住浮动抑或是其他，各国都会运用外汇干预政策，以期保持外汇市场的正常秩序及影响或稳定汇率水平。由此可见，与股票、商品市场等相比，外汇市场上存在中央银行的干预，中央银行的干预对汇率变动和外汇市场的有效性存在着决定性的影响，但是保罗·德格劳威（Paul De Grauwe）和汉斯·杜瓦赫特（Hans Dewachter）一起建立的汇率决定混沌模型并没有考虑具有重要影响的中央银行对外汇市场的干预行为，因此其描述的汇率行为与现实的汇率行为仍存在较大的差距。

杰根森（Jurgensen）报告（1983）将外汇干预定义为“货币当局为影响本国货币的汇率而在外汇市场上进行的外汇买卖活动”[7]。从这一定义可以看出，外汇干预的具体操作是通过在外汇市场上买卖外汇实现的，但归根到底是为了影响本国货币的汇率。因此，中央银行或货币当局的外汇市场干预实质上就是对汇率的干预。

央行在外汇市场上对外汇的干预，主要是通过两个途径来实现的：一是直接干预，通过央行在外汇市场上直接进行外汇交易，改变资产的数量及结构来影响本国货币的汇率；二是间接干预，通过央行所从事的直接干预行为表明央行对本国货币汇率未来趋势的判断和态度来影响市场参与者的心理预期，从而影响本国货币的汇率[8]。通过上述分析可以看出，不管央行采用哪种途径，央行实施的外汇干预措施都相当于给汇率系统的波动输入了一个反馈信号。设是t-1 时期央行的干预量。在引入央行干预后，基本模型中的式（3）为：

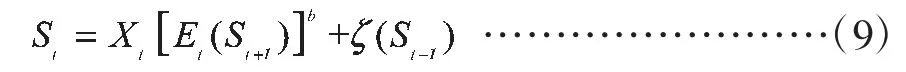
扩展模型中的式（8）应为：

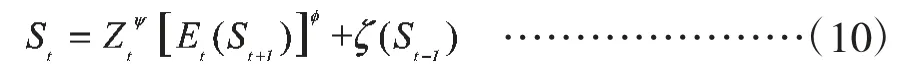
学术界对于外汇干预的目标有几种不同的分类方法。杰根森（Jurgensen）报告(1983)按照时间的长短将外汇干预目标分为长期目标和短期目标，长期目标是指通过外汇干预实现汇率的平滑波动或者接近由基本面确定的均衡水平；而短期目标则是通过外汇干预来纠正无序市场环境。由于通过央行的干预行为来判断央行实施干预的目的是意在长远或者是着眼短期，所以这种分类方法多用于定性分析。德国经济学家Lehment 和Sommer 按照央行的决策标准将外汇干预目标分为四类：平滑干预、趋势中断干预、方向指示干预和其他干预。但在对央行外汇干预目标进行实证研究时，往往更着眼于长期目标和短期目标，一般将外汇干预目标分为平滑汇率波动的干预和实现汇率目标的干预，分别称为“逆风向干预”和“目标干预”[9]。

（一）央行实施“逆风向干预”的汇率决定混沌模型

从长期来看，汇率水平一般会围绕汇率均衡值上下波动，呈现一定的规律性。但是短期情况下，包括市场需求变动在内的各种经济因素以及包括投机资金冲击、市场预期变动、政治因素等在内的很多非经济因素都会导致汇率水平的波动呈现一定的随机性，出现剧烈、单一方向的波动。并且这种短期波动在许多随机因素的影响下很可能继续恶化，进而影响汇率水平的长期稳定，甚至对整个宏观经济都会造成一定程度的负面影响。因此汇率水平的短期大幅单向波动超过宏观经济良好运行所能承受的范围时，央行就应该迅速进入外汇市场，通过相应的外汇干预操作影响或稳定汇率。

根据市场价格的变动机制，在短时期内，本国货币呈现单一上升趋势时，央行就应该进场卖出本国货币，使得本币需求下降，从而阻止价格进一步上升；反之则买入，从而在短期内将汇率维持在一定水平。也就是说，央行缩小外汇市场短期波动趋势的干预必然是逆风向性的，即与市场上汇率的单方向波动趋势方向相反。在短时期内本币通过逆风向干预，央行希望达到降低汇率波动的目标。

因此，央行干预函数可以表示为：

式中，反馈系数β＞0，表明央行总是逆风向干预。

基本模型中，将式（3）带入式（11），得：

扩展模型中，将式（8）带入式（11），得：

扩展模型中，假定技术分析者采用最简单的移动平均模型来预测未来的汇率水平，他们预期未来的汇率水平主要取决于短期移动平均值与长期移动平均值的差值，认为一旦短期移动平均值超过长期移动平均值，汇率则会呈现加速上升，从而得出预期汇率上升的结论；反之，则预期汇率下降。可得：

同时将一期的移动平均视为短期移动平均，而两期的移动平均代表长期移动平均，可得：

上述分析显然与现实存在一定的差距。徐旭初、汤书昆（2005）指出长期事件影响人类心理的程度要明显低于短期事件的影响力，因此技术分析者预期未来汇率更容易受到近期汇率波动的影响，为此对最近一个时期汇率走势的预期形成的影响要进行加权[10]。

因此，式（17）应该修改为：

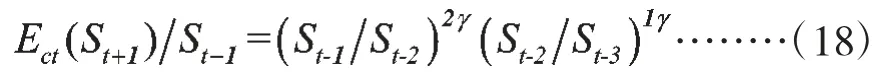
式中2 和1 为所赋权重。

引入央行实施“逆风向干预”后的汇率决定混沌模型表达式改进如下：

基本模型：

扩展模型：

（二）央行实施“目标干预”的汇率决定混沌模型

1973 年，布雷顿森林体系解体后，浮动汇率制度合法化，各国纷纷进行汇率制度改革，采用不同的浮动汇率制度。在浮动汇率制度下，央行允许实际汇率在一定范围内上下波动，理论上是以真实的长期均衡汇率为中心上下波动。如果实际汇率由于经济因素或者非经济因素的影响偏离了预定的波动区间，形成趋势性的、较长时期内的低估或高估，则有可能对整个宏观经济产生不良的影响，此时央行应该进行外汇干预，维持实际汇率在允许波动的区间之内。

一般情况下，当外汇市场供不应求，汇率下降并且突破预定的波动区间时，央行应该卖出外汇，增加外汇供给和减少本币需求，通过调节外汇供求状况，促使汇率回落到预定的区间之内。因此央行实施“目标干预”策略实际上就是如果一国的实际汇率在预定的波动区间内，央行不予干预，任其浮动；如果汇率突破了其预定的波动区间，央行就应该入市买进或者卖出外汇，改变外汇和本币供求，使汇率返回到预定区间之内。

因此，央行干预函数可以表示为：

式中，反馈系数β＞0。β 的大小意味着央行实施外汇干预力度的强弱。如果实际汇率高于均衡汇率，央行干预为负，反之则为正。

基本模型中，将式（3）带入（19），得：

扩展模型中，将式（8）带入（19），得：

和上面分析的一样，技术分析者采用加权平均移动模型预测未来的汇率，则央行实施“目标干预”的汇率决定混沌模型表述如下：

基本模型：

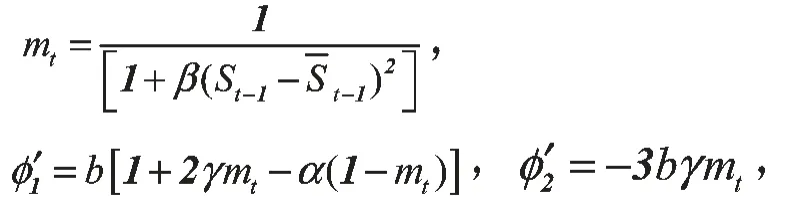
四 结论与展望

混沌分析方法是目前非线性科学的主流研究方法，将混沌分析方法与汇率理论相结合研究汇率决定问题为汇率问题的研究开启了新的研究视角。笔者在介绍和分析Paul De Grauwe 和Hans Dewachter提出的基本汇率决定混沌模型和扩展的汇率决定混沌模型的基础上指出：与股票、商品市场等相比，外汇市场上存在中央银行的干预，中央银行外汇干预已成为政府调节宏观经济活动的重要手段和影响外汇市场供求的重要变量，因此中央银行的干预对汇率变动和外汇市场的有效性有决定性的影响。基于此，笔者在对模型参数进行改造的基础上，依据央行干预外汇市场的目标分类，分别建立了央行实施“逆风向干预”和“目标干预”的汇率决定混沌模型。

下一步的研究工作主要包括两部分：其一，对模型的检验。对模型的检验应该从两方面着手，一方面是模型混沌特性的检验，通过确定模型的参数，分析模型的混沌特性；另一方面是对央行干预效果的检验，即检验央行采取何种干预措施能够有效干预外汇市场。其二，对央行干预外汇市场的建议。后续工作应该在模型检验的基础上，针对央行应该采取的有效措施提出相应的政策建议。