节理体积的计算方法
(中南大学 资源与安全工程学院,湖南 长沙,410083)
工程实践表明,天然岩体中含有大量的节理,有地壳运动所产生的地应力作用形成的节理,有风化作用形成的节理,还有人为因素(爆破、打击等)形成的节理。节理破坏了岩体的完整性,大大降低了岩体的力学性能。因此,节理的力学性质直接影响岩体的力学性质,进而影响岩体工程的稳定与安全。对节理、节理岩体的力学及相关性质的研究,具有极大的工程实践意义。节理的抗剪强度远小于岩石的抗压强度,对节理力学性质的研究主要是对其抗剪性能的研究,众多学者研究表明,节理的剪切强度与节理表面形貌特征有较大关系。Carr等[1−2]运用分形理论来描述复杂的节理表面形貌特征,计算了节理表面的分形参数。杜守继等[3]研究了节理的力学性质与分形参数之间的关系。周枝华等[4−5]运用统计学原理分析了节理表面特征参数的统计分布规律。夏才初等[6−9]定义了节理表面形貌参数,定量描述节理表面的形貌特征。Hutson等[10−14]研究了剪切作用下节理表面的形貌特征变化,并定义了变化度量参数,同时建立了相应的函数式。曹平等[15]研究了节理表面形貌在剪切作用下的变化规律,发现节理表面轮廓角的加权平均值随着剪切次数的增加而减小。杜守继等[16]首次从能量的角度简略分析了节理抗剪强度与表面损伤的关系。但是上述学者没有分析节理抗剪强度与节理体积损失的关系。在众多学者研究的基础上,本文作者运用先进的三维非接触式高精度激光形貌仪,对剪切前后节理表面进行激光扫描测试,从节理表面摩擦的角度,研究了剪切作用下节理体积损失变化规律,分析了抗剪强度与体积损失的关系。
1 节理体积计算公式
在计算体积之前,首先设定一个水平面M,将节理在水平面M以上部分称为节理体积(Joint volume)。在计算整个节理体积时,以与最低谷点相切的平面为水平基准面M,以保证节理表面所有凸起体的体积都包含在计算范围内,水平面M的高度可以随着节理表面凸起体体积计算区域进行调整,节理表面某点到水平基准面M的垂直距离称为节理高度h。为了计算节理在水平面M以上部分的体积,提出节理体积计算的积分式:
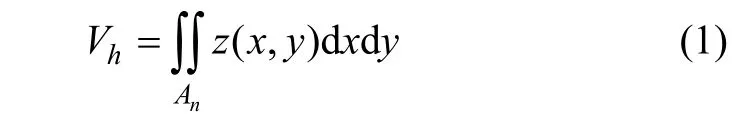
式中:Vh为节理高度为h时水平面M以上部分的节理体积;An为节理表面在水平面M上的投影面积;z(x,y)为节理表面的高度函数;dx和dy分别为An范围内在x和y方向上的微分。
实际的节理表面是一个极为复杂的曲面,用数学函数式来描述这个曲面具有很大的困难,且节理表面特征具有多变性,不同的节理具有不同的表面形貌,需要用不同的数学函数式来表达,即z(x,y)的表达式难以求出,采用式(1)计算节理体积具有相当大的难度。因此,采用离散形式估算节理体积是一种实用的方法。
将节理表面水平投影面积An分别沿x和y方向划分为n个边长为ixΔ,jyΔ的矩形区域,以该矩形为底,向上延伸成一个上表面不规则的近似棱柱体。为了便于计算,将这个棱柱体的上表面简化成一个平面,如图1所示。为了尽可能求得接近棱柱体的真实体积,以式(2)求得棱柱体的平均高zΔ:
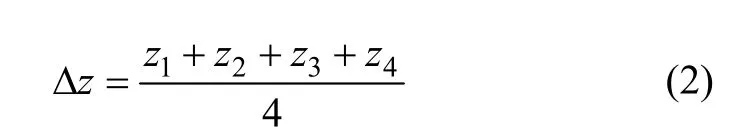
式中,z1,z2,z3,z4分别表示所划分计算区域的近似棱柱体4个角点的高度。

图1 计算区域示意图Fig.1 Schematic diagram of computational domain
Δxi和Δyj分别为计算区域在x和y方向上的长度,这也是节理体积的最小计算单位;i,j分别表示x,y方向上第i,j个计算区域,那么计算区域棱柱体体积Δvi j的计算公式如下:
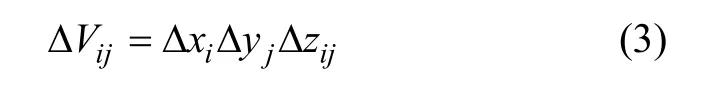
在An范围内,对图1所示的所有计算区域棱柱体的体积求和得
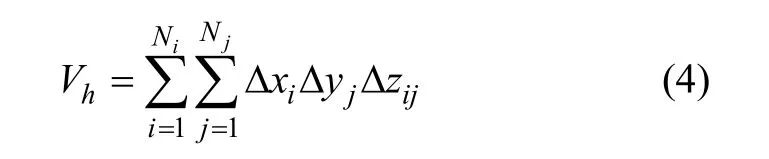
式中:Ni为在An范围内x方向划分小矩形个数总和;Nj为在An范围内y方向上划分小矩形个数总和。
在TalyMap5.0中,将ixΔ和jyΔ设定为单位长度。因此,上文所划分的计算区域为单位区域,单位区域棱柱体体积与其高度直接相关,式(4)简化为:
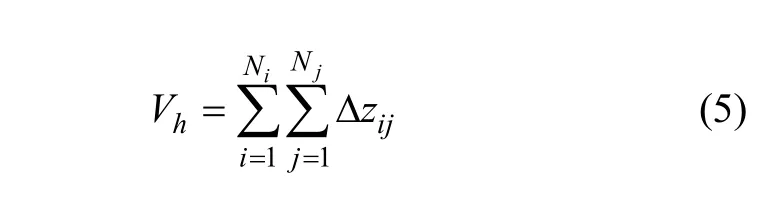
2 举例分析
2.1 扫描仪器介绍
Talysurf CLI 2000三维非接触式高精度激光形貌仪由英国Taylor Hobson公司研制生产。该仪器的主要功能是测试物件表面形态,其外观尺寸(长×宽×高)为800 mm×600 mm×970 mm,质量为280 kg,主要由激光扫描测量装置、控制单元、数据采集软件Talysurf CLI、计算机、数据分析软件 TalyMap5.0组成[15]。
2.2 用TalyMap5.0计算节理体积
图2所示为节理表面某个区域经过放大处理的三维图,节理的最大高度为1.2 mm。从图2可见:整个节理表面由微小凸起体组成。节理表面受到摩擦时,即这些凸起体的磨损破坏。因此,用TalyMap5.0计算节理体积具有很高精度。
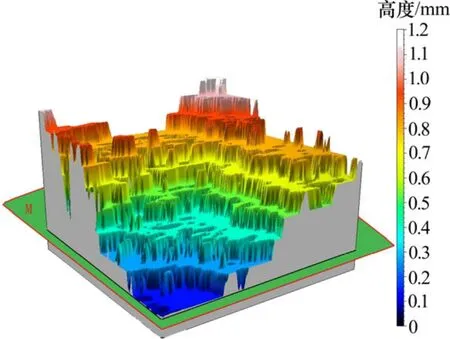
图2 节理表面三维图Fig.2 3D image of joint surface
节理体积计算示意图如图3所示。在TalyMap5.0中,右边工具条中的箭头可以随鼠标上下移动,移动范围为0~hmax。箭头的上下移动代表示水平面M的上下移动,当箭头停止在某个高度时,水平面以上部分的体积和最大高度等参数能够计算出来。同时,可以在节理表面最大高度范围内输入数值来精确确定水平面M的高度,从而计算节理在该高度以上部分的体积。从图3可知:节理表面在中间范围较低,是凹谷部分,左右两端较高,分布着大量凸起体。同时也是容易受到磨损,提供抗剪强度的部分。高度越大,相对应的体积投影面积就越少。利用该功能可以计算和分析节理在不同高度范围内的体积变化以及凸起体磨损情况。
2.3 实例分析
在节理剪切试验过程中发现,如果节理上下盘耦合较差,且法向应力较低时,节理表面磨损较少,且节理的抗剪强度较小,节理的抗剪强度曲线没有明显的峰值抗剪强度。当节理上下盘耦合良好时,节理表面有明显的摩擦痕迹,且抗剪强度曲线有明显的峰值抗剪强度。本文选取节理上下盘耦合良好的情况予以分析。
图 4所示为示例节理的三维图。该节理在x,y方向的长度和宽度分别为72.0 mm和51.5 mm,在z方向的最大高度随着剪切作用发生了变化(如表 1所示)。表2和3所示为在经过2次不同法向应力的剪切作用后,且每次剪切前后,用Talysurf CLI 2000扫描测试,并使用 TalyMap5.0中的体积分析功能计算的结果。
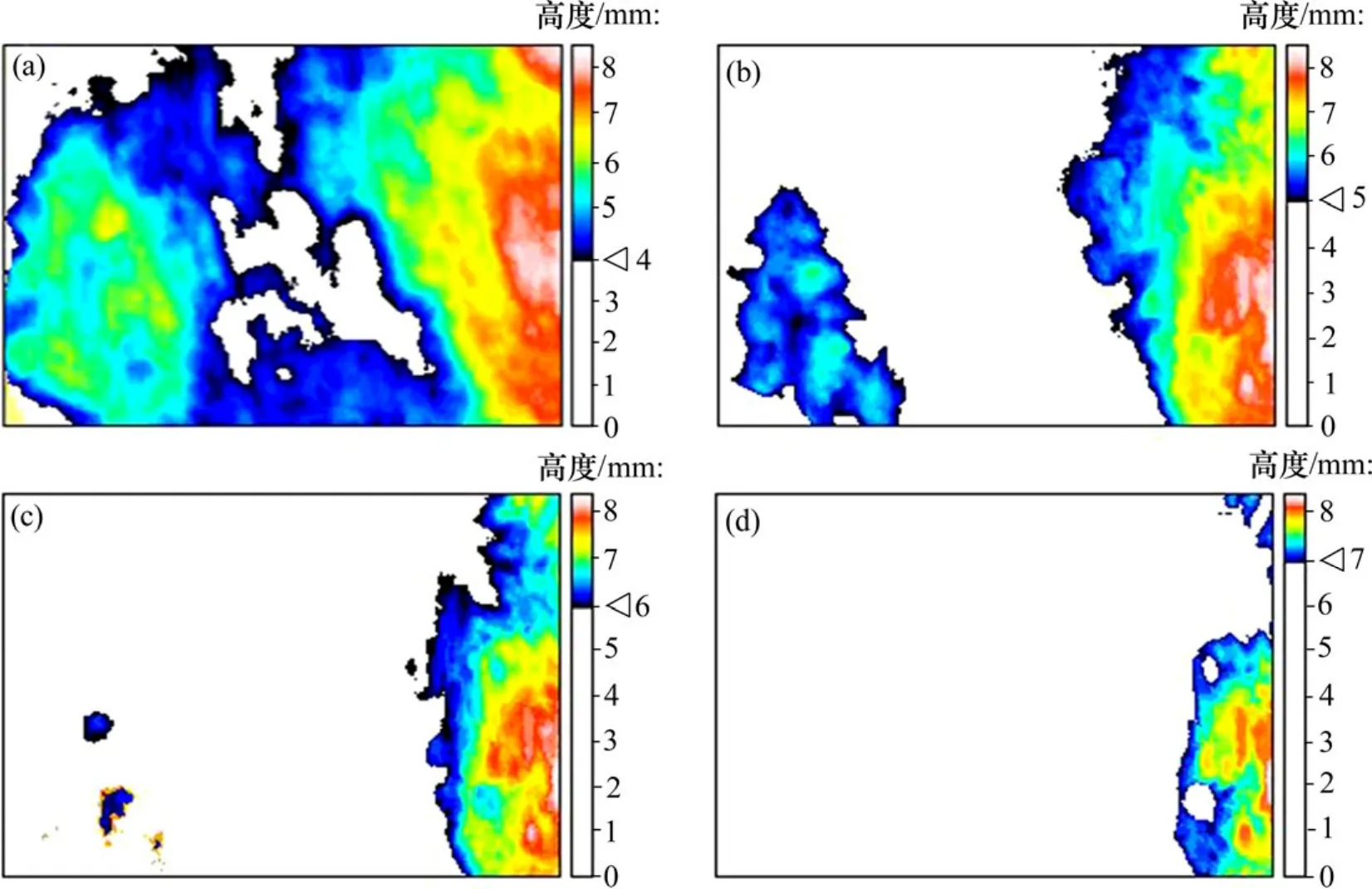
图3 节理体积计算示意图Fig.3 Illustration of computational joint volume on horizontal plane

表1 节理面最大高度值Table 1 Maximum height of joint surface mm
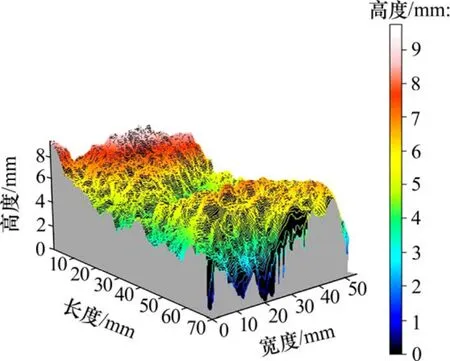
图4 计算节理的三维图Fig.4 3D image of computational joint
从表1可知:经过2次不同法向应力的剪切试验,节理最大高度减小,由剪切前的9.740 mm变为8.544 mm,这是节理体积变化的直接特征。在实际节理剪切过程中,由于剪胀作用的存在,受到磨损的主要是节理面上较高的凸起体,而较低的凸起体不那么容易受到摩擦。从表2可知:剪切作用下节理体积因磨损而减少,由剪切前的20 343.0 mm3减少到剪切1次后的17 240.0 mm3,共减少约3 103.0 mm3,平均高度减少约0.858 mm,最大高度减少1.196 mm,与试验现象一致。第2次剪切后,节理表面最大高度只有8.544 mm,因此,在9 mm以上的节理体积为0 mm3。
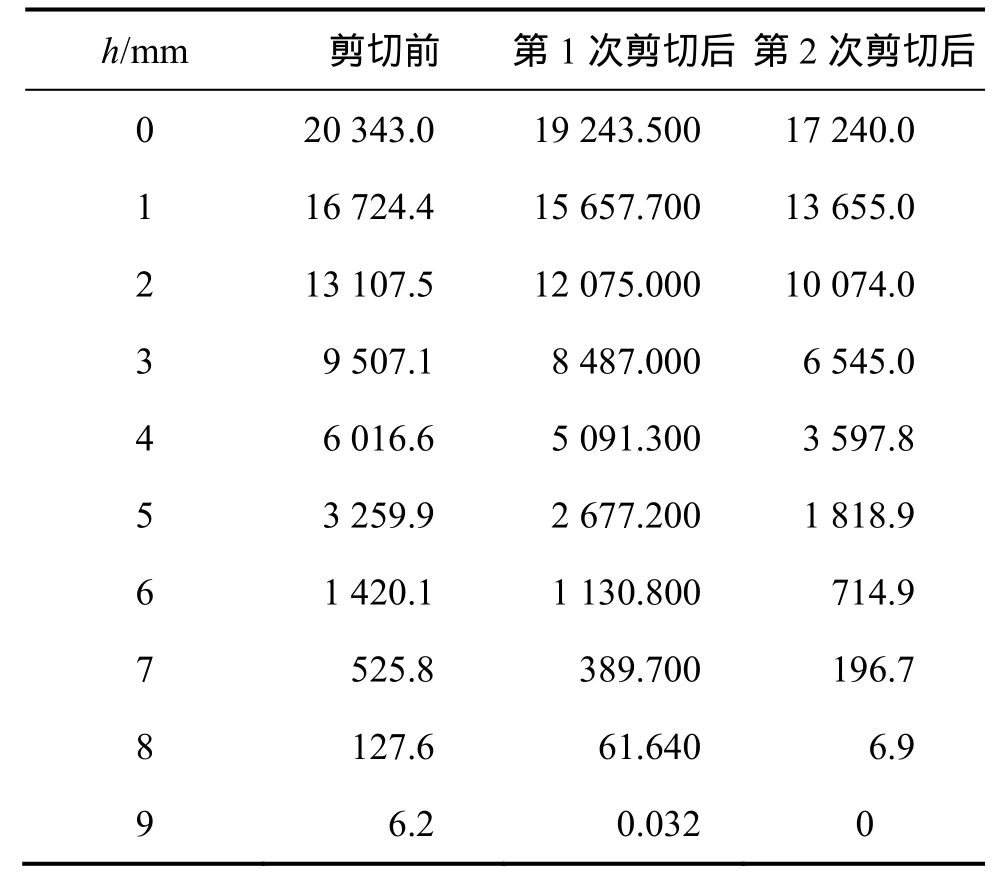
表2 水平面在不同高度上的节理体积Table 2 Joint volume on horizontal plane at different heights mm3
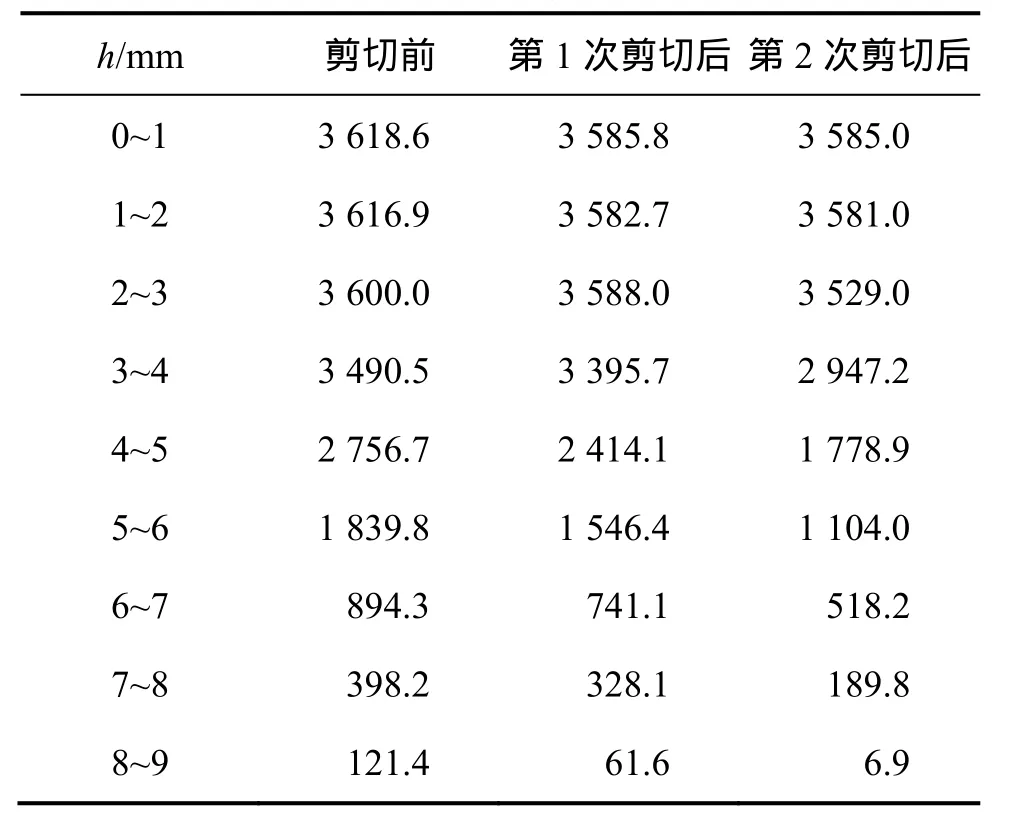
表3 水平面在不同高度范围内的节理体积Table 3 Joint volume between two horizontal planes at different heights mm3
从表3可知:剪切前,在0~1 mm,1~2 mm和2~3 mm高度范围内,节理体积相差不大,说明这段高度范围内节理表面的凸起体较少,所以体积变化不大。2次剪切后,在0~3 mm高度范围内,节理体积变化很少,共减少140.5 mm3,再次说明0~3 mm高度范围内节理表面凸起体较少。节理体积损失主要集中在高度为3~7 mm范围内,由于最高凸起体的体积较小,损失不多,说明节理在耦合良好的情况下,主要是中间高度范围内的凸起体受到摩擦。
计算水平面M在不同高度情况下节理体积的差,可以求得某一指定范围内节理体积,同时可以分析该高度范围内节理面受到的磨损情况,这对于材料摩擦特性的研究具有较大意义。图5所示为水平面位于8 mm处的节理体积计算示意图。由图5可知:剪切作用下,同一节理在相同高度处的投影面积减少,这说明剪切作用使得节理表面的凸起体被剪断,节理表面形貌发生了变化。从表2可得,剪切前,8 mm以上节理体积有 127.60 mm3,但是剪切后,只剩下 6.90 mm3,共损失约120.70 mm3,损失的体积导致8 mm以上节理面高度和投影面积的减小,水平面在 8.544 mm以上的节理体积完全被磨损掉。
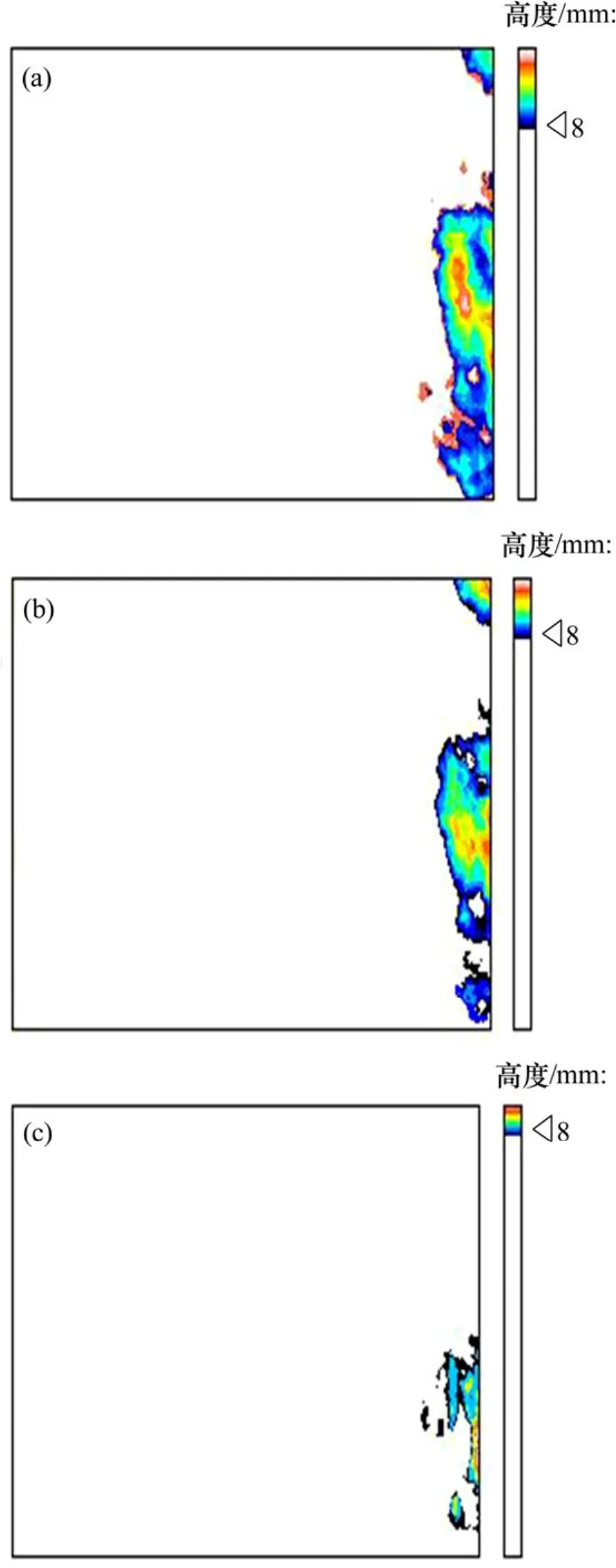
图5 水平面在8 mm处节理体积计算示意图Fig.5 Illustration of computing joint volume on horizontal plane at height of 8 mm
3 结论
(1) 使用Talysurf CLI 2000扫描节理表面具有很高精度,用TalyMap5.0能够准确快速计算指定高度的节理体积。
(2) 在剪切作用下,节理表面高度减小,体积也相应减小,不同法向应力的剪切作用下,相同高度上节理表面体积变化不一致。
(3) 节理上下盘耦合良好时,较高凸起体更易受到磨损,节理体积损失主要集中在中间高度范围内。
[1] Carr J R, Warriner J B. Relationship between the fractal dimension and joint roughness coefficient[J]. Bulletion the Association of Engineering Geologist, 1989, 1151(2): 253−263.
[2] XIE He-ping, WANG Jin-an, XIE Wei-hong. Fractal effect of surface roughness on the mechanical behavior of rock joints[J].Chaos, Solitons & Fractals, 1997, 8(2): 221−252.
[3] 杜守继, 孙钧, 江崎哲郎, 等. 岩体不连续面的几何特性与剪切强度的关系[J]. 同济大学学报, 1999, 27(4): 379−383.DU Shou-ji, SUN Jun, Tetsuro E, et al. Relation of surface roughness and shear strength of rock joints[J]. Journal of Tongji University, 1999, 27(4): 379−383.
[4] 周枝华, 杜守继. 岩石节理表面几何特性的三维统计分析[J].岩土力学, 2005, 26(8): 1227−1232.ZHOU Zhi-hua, DU Shou-ji. 3D statistic analysis of geometrical properties of a rock joint[J]. Rock and Soil Mechanics, 2005,26(8): 1227−1232.
[5] 李庆松, 杜守继. 岩石节理表面三维粗糙特性参数的定量研究[C]//中国岩石力学与工程学会第七次学术大会论文集. 北京: 科学技术出版社, 2002: 91−93.LI Qing-song, DU Shou-ji. Quantitative research of threedimensional parameters for rock joint surface roughness[C]//The 7th Academic Congress of Chinese Society for Rock Mechanics and Engineering. Beijing: China Science and Technology Press,2002: 91−93.
[6] 夏才初. 岩石结构面表面形态特征研究[J]. 工程地质学报,1996, 4(3): 71−78.XIA Cai-chu. A study on the surface morphological features of rock structure faces[J]. Journal of Engineering Geology, 1996,4(3): 71−78.
[7] 夏才初, 孙宗颀, 潘长良. 若干理想表面的形貌参数特征[J].中南矿冶学院学报, 1993, 24(6): 731−737.XIA Cai-chu, SUN Zong-qi, PAN Chang-liang. The parameters characteristics of topography of several ideal surfaces[J]. Journal of Central South Institute of Mining Metallurgy, 1993, 24(6):731−737.
[8] 夏才初, 孙宗颀. 工程岩体节理力学[M]. 上海: 同济大学出版社, 2002: 100−201.XIA Cai-chu, SUN Zong-qi. Joint mechanics of engineering rock mass[M]. Shanghai: Tongji University Press, 2002: 100−201.
[9] Belem T, Homand F, Souley M. Quantitative parameters for rock joint surface roughness[J]. Rock Mechanics and Rock Engineering, 2000, 33(4): 217−242.
[10] Huston R W, Dowding C H. Joint asperity degradation during cyclic shear[J]. International Journal of Rock Mechanics and Mining Science and Geomechanics, 1990, 27(2): 109−119.
[11] Homand F, Belem T, Souley M. Friction and degradation of rock joint surfaces under shear loads[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001,25(10): 973−999.
[12] Riss J, Gentier S, Sirieix C, et al. Degradation characterization of sheared joint wall surface morphology[C]//American Rock Mechanics Association, 2nd North American Rock Mechanics Symposium Rock Mechanics. Aubertin, Hassani, Mitri(eds).Balkema: Rotterdam, 1996: 1343−1349.
[13] Fox D J, Kana D D, Hsiung S M. Influence roughness on dynamic shear behaviour in jointed rock[J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 35(7): 923−940.
[14] Lee H S, Park Y J, Cho T F, et al. Influence of asperity degradation on the mechanical behavior of rough rock joints under cyclic shear loading[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(7): 967−980.
[15] 曹平, 范祥, 蒲成志, 等. 节理剪切试验及其表面形貌特征变化分析[J]. 岩石力学与工程学报, 2011, 30(3): 480−485.CAO Ping, FAN Xiang, PU Cheng-zhi, et al. Shear test of joint and analysis of morphology characteristic evolution of joint surface[J]. Chinese Journal of Rock Mechanics and Engineering,2011, 30(3): 480−485.
[16] 杜守继, 江崎哲郎, 蒋宇静, 等. 岩石节理的剪切破坏特性的定量分析[C]//中国岩石力学与工程学会第五次学术大会论文集. 北京: 中国科学技术出版社, 1998: 239−244.DU Shou-ji, Tetsuro E, JIANG Yu-jing, et al. The quantitative evaluation of surface damage of rock joint during shear processes[C]//The 7th Academic Congress of Chinese Society for Rock Mechanics and Engineering. Beijing: China Science and Technology Press, 1998: 239−244.

