基于单神经元复合整定的多余力抑制

(西北工业大学 自动化学院，陕西 西安，710129)

电液负载模拟器是飞行器在设计阶段进行地面半物理仿真的主要设备之一，它通过模拟作用在飞行器舵面上的气动载荷，考察系统的各项指标，发现设计中的不足。在电液负载模拟器的地面半物理仿真过程中，多余力的抑制问题是伺服加载控制的难点[1−2]。多余力是由承载对象的位置运动引起的，会严重影响系统的加载精度。目前，多余力的消除主要基于结构不变性原理，通过对舵机位移信号的前馈补偿，使干扰对系统的作用正负相消进而消除多余力。该方法在理论上需要引入干扰信号的速度项、加速度项以及加速度的变化率来进行补偿，具有较强的微分环节，这在物理上是难以实现的，通常采用配极点的方法解决该矛盾。极点的引入使得前馈补偿作用的频带变窄，当频率逐渐增大，多余力的消除效果逐渐减弱。其次加速度的变化率在实际中不易获得，一般可以忽略，采用近似补偿的方案。基于前馈补偿的不足，文献[3]提出利用舵机伺服阀的控制信号进行速度同步控制抑制多余力的新方案，取得了有效的成果，但其所需要的信号不易获得；文献[4]采用在非线性前馈校正基础上的模糊自适应控制策略，较好地消除了多余力，但其需要建立模糊控制器的参考模型，过程复杂。一些学者在分析多余力的产生机制后，提出位置同步补偿的方法，目的是保证负载模拟器和舵机的同步运动进而消除多余力。按信号来源的不同，位置同步补偿分为主动补偿与随动补偿[3]。主动补偿的同步信号取自舵机系统的指令信号，其同步精度取决于2个系统控制特性的一致程度，做到同步困难较大，往往会出现过补偿的现象。随动补偿的同步信号取自舵机系统的输出位置信号，只需要设计和调整自身的参数，保证同步系统的幅频特性平坦、相位变化不大，就可以达到很好的效果，不会出现过补偿，但要完全消除多余力仍然困难，而且其参数需要随着舵机频率、幅值的变化而进行调节，自适应能力较差。文献[5−6]采用CMAC与PID并行控制方法，自适应能力强，但神经网络控制研究侧重于没有干扰时控制方法的收敛性与稳定性，对于舵机运动存在噪声的情况有待探讨；文献 [7−8]引入H∞控制方法，但其需要建立系统的精确数学模型；文献[9]引入滑模控制的方法，但其抖振抑制问题往往需要结合不同的条件考虑，增加了控制的难度。鉴于随动补偿方法结构简单，多余力抑制效果好，本文作者利用神经网络自适应能力强的优点提出了基于单神经元PID的复合方案，对随动补偿环节中的参数进行整定。

1 系统简述及建模

1.1 系统结构简述

系统的结构原理如图1所示。由图1可知：舵机系统输入给定的位移信号，并与位移传感器构成闭环，控制舵机运动；加载系统输入给定的载荷谱信号，并与力传感器构成闭环，输出所需载荷。舵机的运动带动加载系统一起运动，在此过程中形成强干扰，产生了多余力。由于本文采用随动补偿的方法，与舵机的相关性较弱，故只考虑加载系统的数学模型。

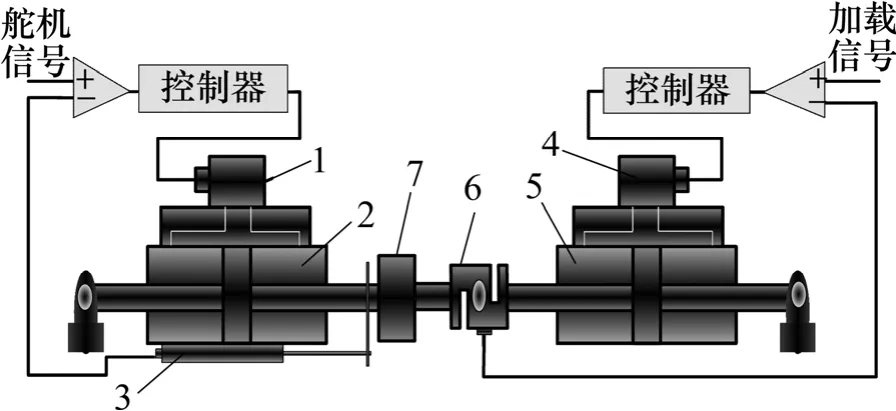
图1 电液负载模拟器原理结构图Fig.1 Structure chart of electro-hydraulic load simulator

1.2 模型的建立[10]

(1) 伺服阀流量线性化方程为：

式中：Qf为负载流量，m3/s；xv为伺服阀阀芯位移，m；Pf为液压缸两端产生的负载压降，Pa；KQ为伺服阀流量系数；KC为伺服阀流量−压力系数。

(2) 液压缸流量连续方程为：

式中：t为时间；At为液压缸活塞的有效截面积，m2；Vt为液压缸的有效容积，m3；xt为液压缸的位移，m；Ey为等效容积弹性模量，N/m2；Csl为液压缸的总泄漏系数，m5/(N·s)。

(3) 力平衡方程为：

式中：F为液压加载缸的输出力，N；mt为运动部分折算到活塞上的总质量，kg；Bt为液压缸活塞运动的黏性阻尼系数，N·s/m。

(4) 伺服阀阀芯位移传递函数为：

式中：ksv为伺服阀输入增益；u为伺服阀控制输入。

(5) 加载缸输出力方程为：

式中：Kt为负载弹簧刚度，N/m；xy为受控对象输出位移。

对式(1)～(5)进行拉氏变换并整理，系统的数学模型如图2所示。

图2 加载系统数学模型Fig.2 Mathematical model of loading system

2 单神经元PID的基本原理

单神经元PID控制器不仅结构简单，而且现场调试参数少，能够适应环境变化，具有较强的鲁棒性[11]。其结构原理如图3所示。

图3 单神经元PID原理Fig.3 Principle of single neuron PID

图3中控制器的输出为：

单神经元的特性取为：

式中：Δu(k)为单神经元在k时刻的输出；K为单神经元的比例系数；wi(k)为单神经元在k时刻的调整权值；xi(k)为单神经元在k时刻的输入。

为了使单神经元具有PID特性，取单神经元的输入xi(k)为：

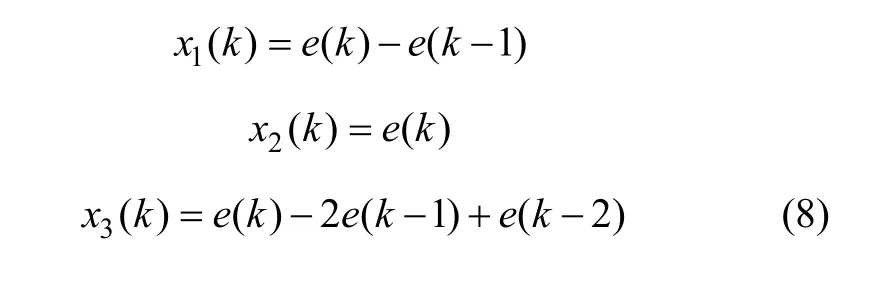
其中：x1(k)为误差的一阶微分；x2(k)为当前误差；x3(k)为误差的二阶微分；e(k)为k时刻系统输入误差。

将式(8)代入式(7)并与常规PID比较，可知单神经元PID通过调整权值来改变PID参数，实现参数的自整定。权值wi(k)的调整可以采用不同的学习算法，目前常用的学习算法有无监督的 Hebb学习算法和有监督的Delta学习算法。

文献[11−15]均采用无监督与有监督相结合的学习算法，采用有指导的学习对环境信息进行自组织来产生控制作用，能够适应模型的不确定性与环境的变化，鲁棒性好。该学习算法为：

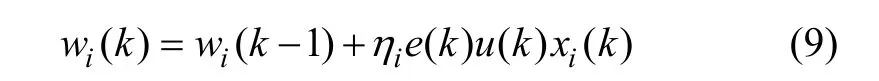
式中：ηi为神经元的学习速率。

3 控制器设计

加载系统的控制器设计如图4所示。

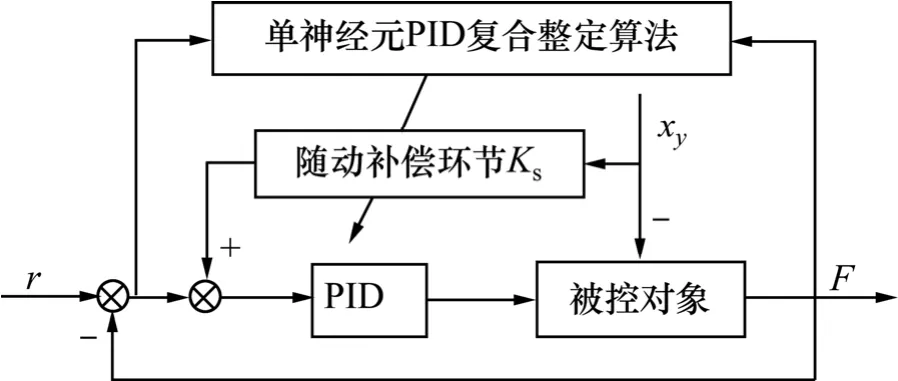
图4 控制器原理结构图Fig.4 Structure chart of controller

对于电液伺服加载系统控制器的设计思路，首先要保证在没有舵机位移强干扰的情况下，系统能够迅速跟踪给定信号。传统PID控制器具有鲁棒性好、跟踪迅速的优点，同时考虑微分环节对噪声的敏感性，故只采用PI控制的方式，在无舵机干扰的情况下，性能优异。其次，当舵机运动时，多余力与舵机位移干扰的频率相同、幅值不同，且二者在低频率时相移基本为半个周期(图 5所示)，故采用随动补偿的策略，施加与多余力频率相同、幅值相反的信号，以期望实现多余力的有效抑制。

为了确定幅值，选择单神经元PID对其进行自整定，但由于舵机干扰与多余力之间的相位差仅近似半个周期，难以完全补偿多余力，导致系统误差始终不为0，即单神经元PID的输入始终不为0，整定结果出现周期性震荡。整定结果如图6所示。

图5 干扰输入下的幅频特性Fig.5 Amplitude-frequency characteristic of disturbance input

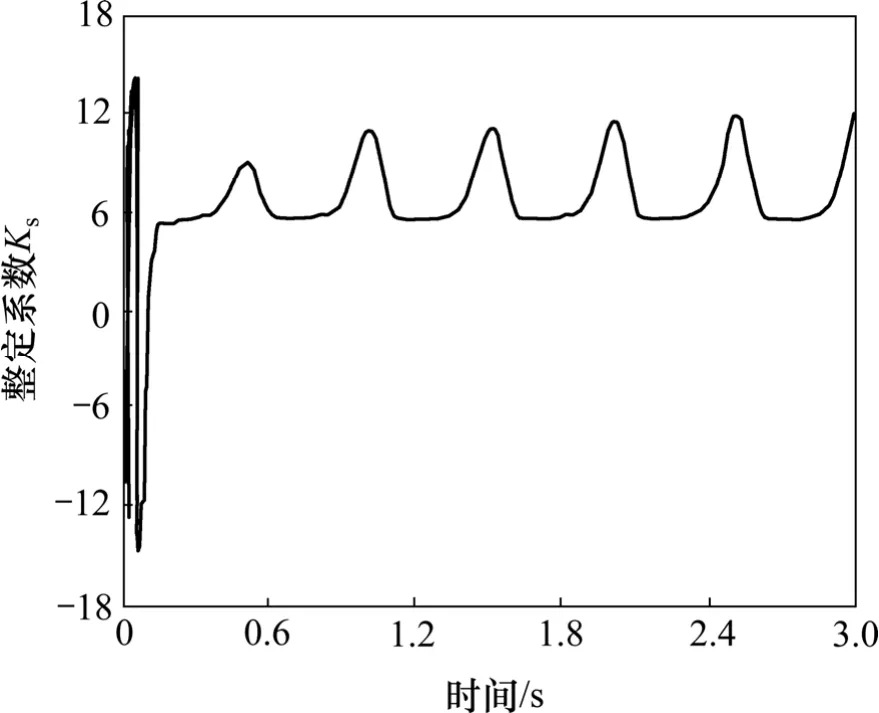
图6 单神经元PID整定结果Fig.6 Tuning output of single-neuron PID

通过仿真，并对单神经元PID的整定结果分析，发现周期震荡的最小值为补偿参数的最优值。因此，可以对单神经元PID的输出进行修正，使其稳定在最优值处；同时引入系统输出作为观察信号，当其没有被控制在有效范围内时，重新整定。

上述控制思路对于载荷指令为恒定值是有效的，但是当载荷指令为正弦变化时存在一定的缺陷。由于引入了系统输出作为观察信号，当系统输出按正弦变化时，会使该算法不断地重新整定。实际应用中，载荷指令信号通常是已知的，可以对其进行适当修改以弥补整定算法的不足。假设输入信号为如下形式：

修改指令信号为：

式中：a0为信号均值；a1为信号幅值；g(t0)为在t0时刻的阶跃函数；t0为设定值。

调整加载指令后，该算法可将参数调整至最优，进而有效抑制多余力。单神经元PID输出的修正算法如下：

(1) 为了迅速使单神经元PID输出趋于最优值，在系统工作的初始时刻(小于某设定时间)，不对整定结果修正；

(2) 当初始时刻结束，初始化 1个标志位，并对整定结果更新迭代，与上一时刻的值进行比较，若取得最小值，则置标志位；

(3) 若标志位被置位，则输出始终保持在最小值；

(4) 若标志位被置位，且当前时刻小于t0时，询问观察信号是否大于某设定值，若大于则重新整定；

(5) 若当前时刻大于t0，不再询问观察信号。

4 仿真与分析

电液负载模拟器的参数取为：mt=9 kg，At=0.001 347 m2，Vt=8.1×10−4m3，Bt=300 N·s/m，Ey=7×108N·m−2，KQ=0.98 m2/s，ksv=0.04 m/A，KC=4.7×10−11m5/(N·s)，Csl=2×10−11m5/(N·s)，Kt=8×106N/m。PID控制器：比例系数kp=1.2×10−7，积分系数ki=1.05×10−4，微分系数kd=0，单神经元PID控制器：单神经元学习速率η1=100，η2=20，η3=5，单神经元比例系数K=0.000 1。随动补偿环节中增益系数：KS=θ×104，其中，θ为单神经元复合整定算法的输出。

基于前文分析，对单神经元PID综合控制进行仿真研究，并与传统的前馈补偿进行比较。设定加载信号为 0，舵机运动为 0.065sin(2πft)，并假定该运动不含噪声。仿真结果如图7和图8所示。比较图7和8可知：由于前馈补偿中配置了极点，使得前馈补偿作用的频带变窄，频率越高则抑制效果越差。在系统允许的范围内，一般不考虑初始时刻的多余力冲击。由此可见，相对于广泛使用的前馈补偿，单神经元综合控制有着明显的优势。

图7 f=0.5 Hz时多余力曲线Fig.7 Curves of surplus force at 0.5 Hz

图8 f=2 Hz时多余力曲线Fig.8 Curves of surplus force at 2 Hz

在实际工程应用中，由于现场情况复杂，来自舵机的干扰信号中往往存在噪声。仿真时为了模拟实际环境，在舵机干扰中加入白噪声，进而考察单神经元综合控制器的性能。设定加载信号为 0，舵机运动为Asin(2πft)。仿真结果如图9和图10所示。

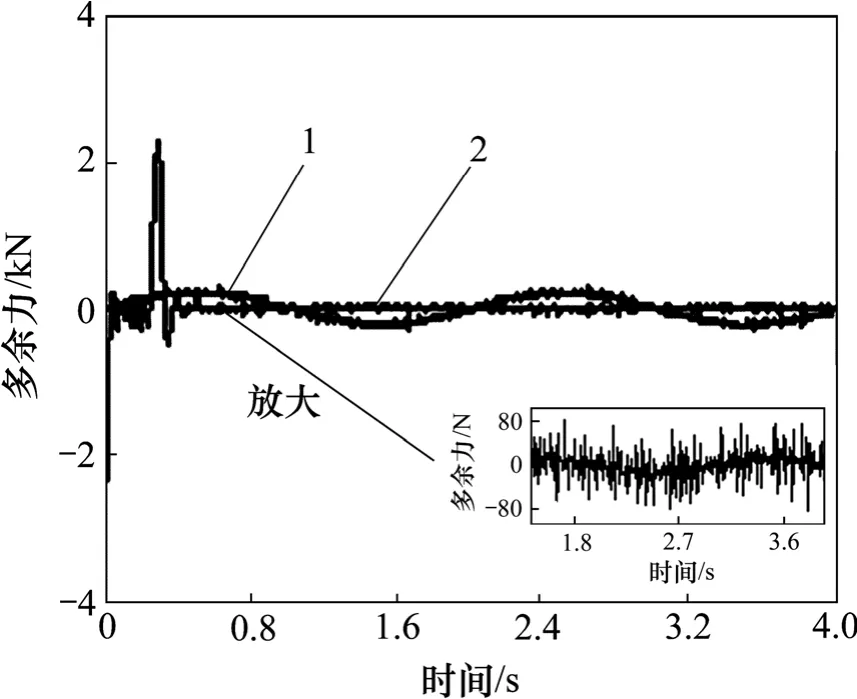
图9 f=0.5 Hz，A=0.065 m时多余力曲线Fig.9 Curves of surplus force at f=0.5 Hz, A=0.065 m

图10 f=4 Hz，A=0.035 m时多余力曲线Fig.10 Curves of surplus force at f=4 Hz, A=0.035 m

由图9和图10可知：f=0.5 Hz，幅值A=0.065 m时，多余力基本控制在−80～80 N 范围内，f=4 Hz，A=0.035 m时，多余力基本控制在−200～200 N范围内。当舵机运动频率增加时，多余力抑制效果减弱。这是由于实际补偿信号与理想值存在相位差，当舵机频率增加时，相位差也增加。鉴于舵机的运动一般频率较低，且上述多余力能够满足控制指标要求，故不对相位问题进行讨论。

为了考核控制器在给定载荷信号下抑制多余力的能力，设定加载信号为30 000+6 000sin(20πt)，舵机运动为 0.065sin(4πt)，并加入白噪声。由于输出信号滞后于加载指令，不宜将误差信号作为考察指标，因此将系统在无舵机干扰时的输出与有舵机干扰时的输出相比较，将两者之差作为考察指标。仿真结果如图11所示。

图11 加载系统跟踪曲线Fig.11 Tracking curves of loading system

5 结论

(1) 在传统的前馈补偿方案中，由于引入了极点，使得前馈补偿作用的频带变窄，当频率逐渐增大，多余力的消除效果逐渐减弱。随动补偿控制结构简单，但受舵机运动频率、幅值的影响，其参数需要反复调整，自适应能力差。

(2) 基于单神经元PID的综合控制方案能够迅速整定随动补偿环节中的参数，使多余力被有效抑制。该控制方案结构简单，自适应能力强，具有实际意义。

[1] Yoonsu N, Sung K H. Force control system design for aerodynamic load simulator[J]. Control Engineering Practice,2002(10): 549−558.

[2] Jiao Z X, Gao J X, Hua Q, et al. The velocity synchronizing control on the electro-hydraulic load simulator[J]. Chinese Journal of Aeronautics, 2004, 17(1): 39−46.

[3] 焦宗夏, 华清, 王晓东, 等. 电液负载模拟器的复合控制[J].机械工程学报, 2002, 38(12): 34−38.JIAO Zong-xia, HUA Qing, WANG Xiao-dong, et al. Hybrid control on the electro-hydraulic load simulator[J]. Chinese Journal of Mechanical Engineering, 2002, 38(12): 34−38.

[4] 蔡永强, 裘丽华, 王占林. 力伺服系统的模糊自适应控制[J].北京航空航天大学学报, 1999, 25(1): 22−25.CAI Yong-qiang, QIU Li-hua, WANG Zhan-lin. Adaptive fuzzy control for loading servo system[J]. Journal of Beijing University of Aeronautics and Astronautic, 1999, 25(1): 22−25.

[5] 刘伟杰, 王志胜, 甄子洋. 电动负载模拟器的 CMAC神经网络复合控制[J]. 电光与控制, 2009, 16(9): 89−91.LIU Wei-jie, WANG Zhi-sheng, ZHEN Zi-yang. CMAC neural network control on electrical load simulator[J]. Electronics Optics & Control, 2009, 16(9): 89−91.

[6] 石旭东, 张发, 荆涛, 等. 飞行模拟机电动操纵负荷系统控制与仿真[J]. 电机与控制学报, 2010, 14(5): 73−78.SHI Xu-dong, ZHANG Fa, JING Tao, et al. Control and simulation of electric control loading system of flight simulator[J]. Electric Machines and Control, 2010, 14(5): 73−78.

[7] 罗璟, 赵克定, 许宏光. 基于 Η∞鲁棒控制的电液负载模拟器的性能研究[J]. 机床与液压, 2006(8): 113−116.LUO Jing，ZHAO Ke-ding, XU Hong-guang. Study on performance of electro-hydraulic load simulator based on H∞robust control[J]. Machine Tool & Hydraulics, 2006(8):113−116.

[8] 孙以泽, 赵慧, 韩俊伟, 等. 舵机加载系统H∞控制的研究[J].船舶工程, 2001(2): 40−43.SUN Yi-ze, ZHAO Hui, HAN Jun-wei, et al. Research ofH∞control in steering gear load system[J]. Ship Engineering,2001(2): 40−43.

[9] 张菊丽. 舵机动态加载系统控制仿真研究[D]. 西安: 西北工业大学自动化学院, 2007: 46−62.ZHANG Ju-li. Simulation study of the rudder dynamic loading system control[D]. Xi’an: Northwestern Polytechnical University.School of Automation, 2007: 46−62.

[10] 王春行. 液压伺服控制系统[M]. 2版. 北京: 机械工业出版社,1987: 68−71.WANG Chun-xing. Hydraulic servo control system[M]. 2nd ed.Beijing: China Machine Press, 1987: 68−71.

[11] 丁军, 徐用懋. 单神经元自适应PID控制器及其应用[J]. 控制工程, 2004, 11(1): 27−30.DING Jun, XU Yong-mao. Single neuron adaptive PID controller and its applications[J]. Control Engineering of China,2004, 11(1): 27−30.

[12] Wang Y Q, Sun F, Liu J, et al. Application of Smith Predictor Based on Single Neural Network in Cold Rolling Shape Control[J]. Chinese Journal of Mechanical Engineering, 2009,22(2): 282−286.

[13] 张建峡, 杨勇, 许德志, 等. 单神经元自适应PID控制交流调速系统[J]. 电机与控制学报, 2007, 11(2): 130−133.ZHANG Jian-xia, YANG Yong, XU De-zhi, et al. Single neuron adaptive PID control for AC Variable-speed system[J]. Electric Machines and Control, 2007, 11(2): 130−133.

[14] 徐英, 徐用懋, 杨尔辅. 时变大纯滞后系统的单神经元预测控制[J]. 清华大学学报: 自然科学版, 2002, 42(3): 383−386.XU Ying, XU Yong-mao, YANG Er-fu. Single-neuron predictive control for time-variable large delay systems[J]. Journal of Tsinghua University: Science and Technology, 2002, 42(3):383−386.

[15] 王伟, 高晓智, 王常虹, 等. 免疫调节增益的单神经元PID控制器[J]. 电机与控制学报, 2008, 12(1): 74−79.WANG Wei, GAO Xiao-zhi, WANG Chang-hong, et al. New single neuron PID controller based on immune tuning[J].Electric Machines and Control, 2008, 12(1): 74−79.