减震弹簧故障下直线筛力学模型突变研究

彭利平，刘初升，王 宏

(中国矿业大学 机电工程学院，江苏 徐州 221116)

振动筛在强交变载荷下受迫振动，易发生疲劳损坏或破坏。目前，国内外对振动筛筛体、横梁等结构损坏的研究较多［1－4］，而对减震弹簧故障研究的相关报道很少［5］。在实际生产过程中常有减震弹簧严重扭曲变形、互相啃螺旋等弹簧损坏，致使筛箱两侧板对称点的振幅差不满足设计要求，破坏了振动筛的工作稳定性，进而产生其他结构损伤。实际生产过程中，对于弹簧断裂等严重变形现象，可直接观察;而对于疲劳等引起的弹簧故障，其外部特性变化不明显，只能借助振动筛力学特性间接判断。此时，振动筛减振弹簧故障的力学表现主要为弹簧刚度值的变化。国内外对于刚度变化下振动系统的动力学特性已进行了相关研究［6，8－10］，基于此，针对减振弹簧故障下的直线筛系统，假设故障程度相同，即故障弹簧刚度值相等，表1定性分析了不同弹簧健康状态组合下直线筛的力学特性(×—弹簧故障，○—弹簧无故障)，不难看出，减震弹簧故障下直线筛的力学特性表现更为丰富，因此传统的基于各弹簧相同条件下建立的直线筛单自由度模型无法表征弹簧故障下系统全部力学特性。本文从传统的直线筛单自由度模型出发，分析并建立了其二、三自由度突变模型，讨论了系统向多自由度方向模型突变的可能性，并利用数值方法对各模型间突变过渡过程进行了仿真分析，得出了系统在时域内刚度变化引起的力学特性变化。

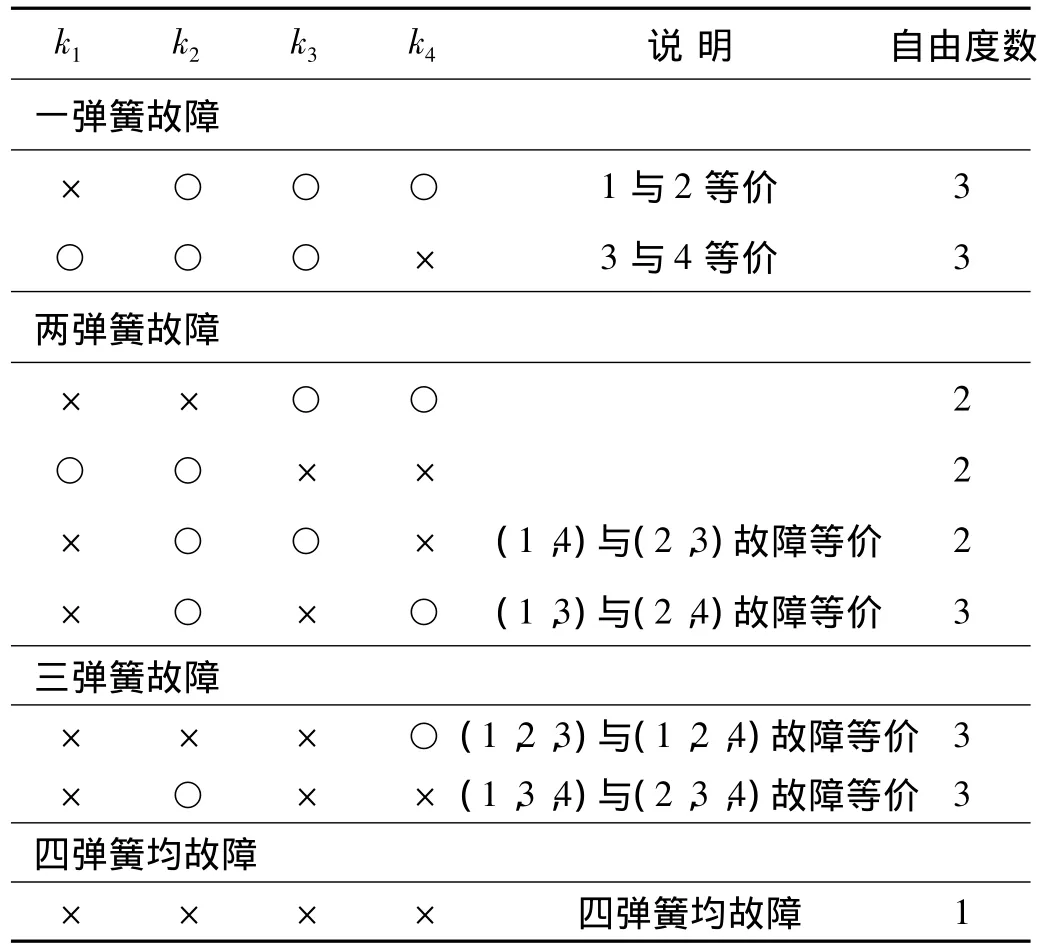
表1 减震弹簧健康状态组合Tab.1 Combinations of health state of damping springs

1 传统单自由度(1－DOF)模型

传统的直线筛筛面水平，在非水平布置的两激振器协同作用下，筛箱在激振力方向上来回振动，筛面运动轨迹与水平方向成一定倾角，即振动方向角。为简化建模，方便与以下的多自由度模型作对比，这里采用筛面倾斜而激振器水平布置的方式，构成的单自由度直线筛(图1(a)、图1(b))的激振器所产生的离心力经过振动筛质心，且始终保持竖直方向，从而使筛体在竖直方向上作往复直线运动，实现物料的筛分与传送。

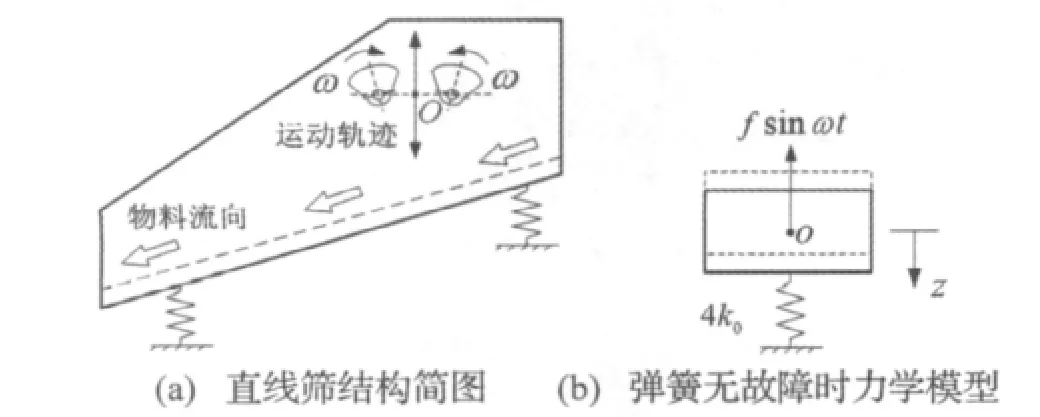
图1 传统单自由度直线筛结构简图及动力学模型Fig.1 Structural sketch and dynamic model of traditional 1－DOF liner vibrating screen

动力学方程为:

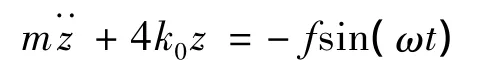
假设系统模型突变时迅速到达到稳态振动状态，即:

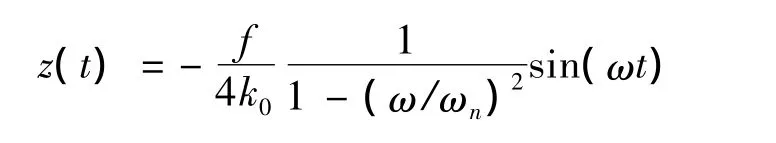
2 突变模型

2.1 二自由度(2－DOF)突变模型

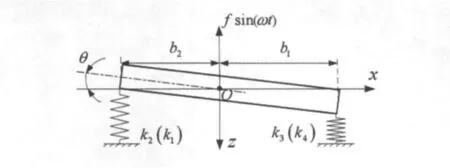
图2 二自由度力学突变模型Fig.2 2－ DOF catastrophic model

强交变载荷下，当弹簧健康状况为两弹簧发生故障时，对振动特性的表示可能需要两个广义变量，由于激振电机的能量补偿，系统运动稳定时可忽略其阻尼的影响，传统单自由度模型突变为二自由度模型(图2，广义变量为z，θ)。该模型中，以激振中心O为原点建立坐标系，O点同时为振动筛计算质心;各弹簧刚度分别为 k1、k2、k3、k4，绕物料进、出口方向(x 轴方向)上弹簧1(2)、3(4)到原点的水平距离分别为b1、b2，激振力为fsin(ωt);筛面竖直方向的相对于静平衡位置的跳动位移为z，绕y轴摆动的转动惯量为Jy，角位移为θ。

图2模型所对应动力学方程为:

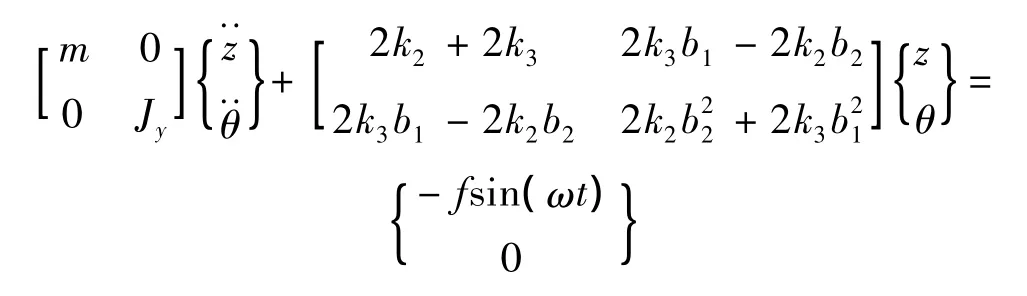
系统固有频率可由系统特征方程计算得到，其稳态振动可利用求解多自由度无阻尼系统强迫振动的振型叠加法求得［11］。很明显，该模型尤指表1中两弹簧发生故障且刚度满足k1=k2≠k3=k4的弹簧健康状态，而对于k1=k4≠k2=k3的情况，模型失效，但此时的力学模型与图2类似，不另给出。

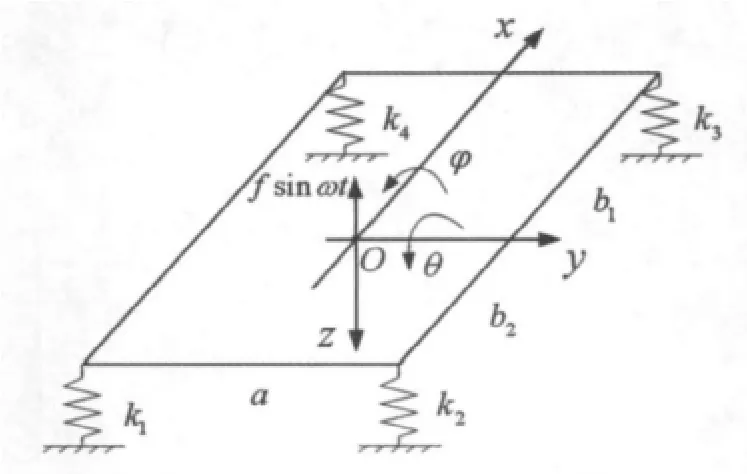
图3 三自由度力学突变模型Fig.3 3－ DOF catastrophic model

2.2 三自由度(3－DOF)突变模型

弹簧健康状况组合如表1中一弹簧故障或三弹簧故障时，其振动形式是空间上的上下跳动，左右、前后翻转的振动组合，筛体具有三个自由度(z，φ，θ)。由于激振电机的能量补偿，可以忽略系统阻尼对系统稳定状态下的影响。在建立其三自由度突变动力学模型(图3所示)时进行了以下几点假设［7］:

(1)振动筛筛面的弹性变形相对于弹簧变形可以忽略不计，即将筛面视为刚体，始终保持平面状态;

(2)弹簧微小损坏下引起的振动筛摆动幅度很小，可近似认为弹簧始终保持竖直方向的形变。

该模型仍以振动筛计算质心及激振中心O为坐标原点。各弹簧刚度分别为k1、k2、k3和k4，y轴方向上弹簧1、2到原点的水平距离均为a/2，其他模型特征如2.1中所述。

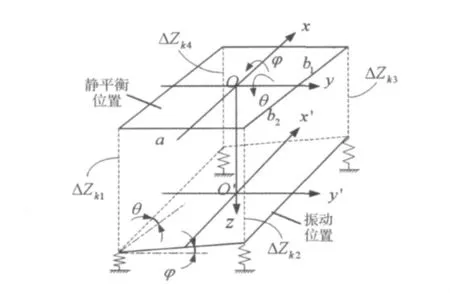
图4 减振弹簧压缩形变量的计算示意图Fig.4 Calculation schematic diagram for the compressed deformation of damping springs

根据图4所示筛面某一时刻的振动位置相对于静平衡位置的相对关系，各弹簧的压缩形变量用三个广义自由度可以表示为:

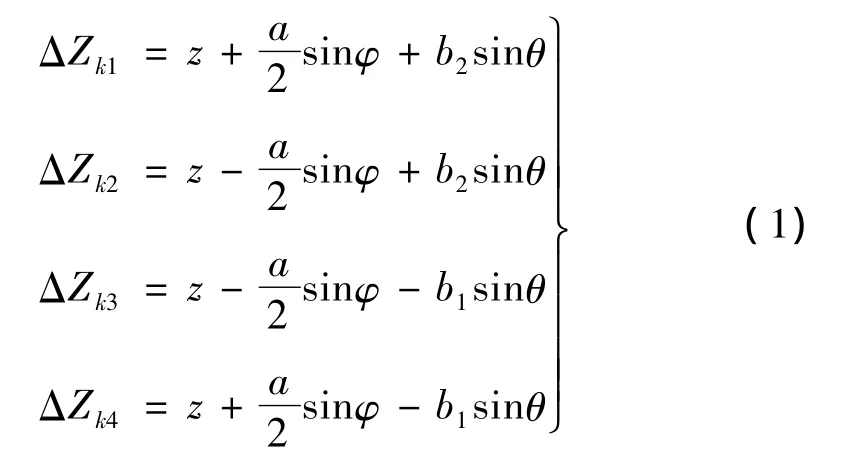
考虑到建立模型时假设的弹簧微小损坏下引起的振动筛摆动幅度很小，于是有:

将式(2)代入式(1)得:

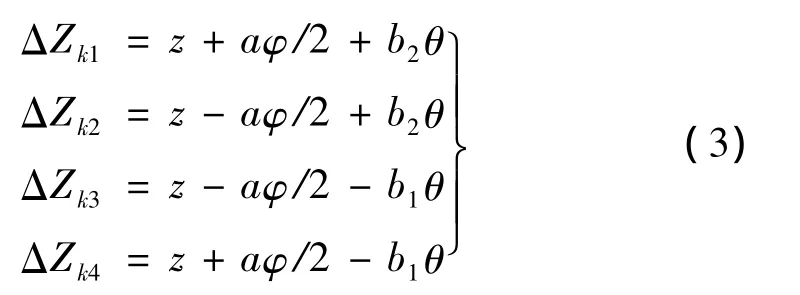
即为振动筛无阻尼振动时筛体与减振弹簧连接处上压板在竖直方向上的振动位移，对其通过一次、二次微分可以得到上压板的振动速度及加速度。

对于一个n自由度的系统，其振动微分方程可由以下拉格朗日方程建立:

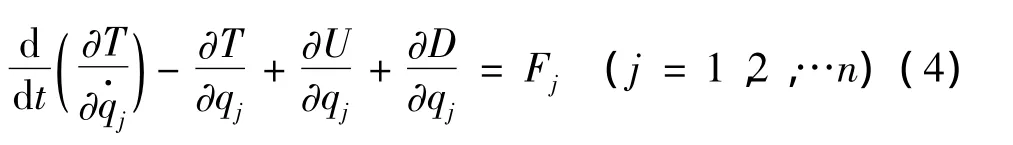
其中，qj为系统的广义坐标为系统广义速度，T为系统的动能，U为系统势能，D为系统的能量耗散函数，Fj为广义激振力。

对于本文中的振动筛系统，依次有:

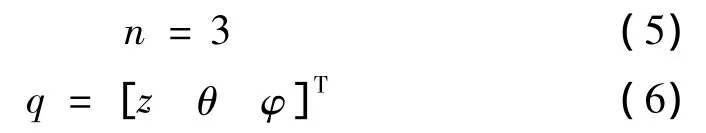
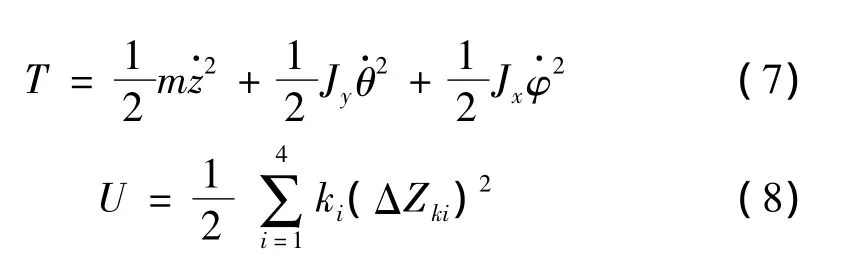
由于是简谐力强迫振动，运动稳态情况下可以忽略阻尼的影响，即:

将式(3)、式(5)～式(9)代入式(4)，整理后即可得到该无阻尼系统强迫振动微分方程:

式中:

位移向量x=［z θ φ］T

外力向量F=［－fsinωt 0 0］T

质量矩阵:

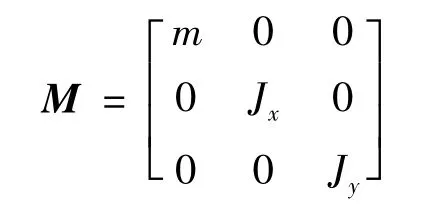
刚度矩阵:

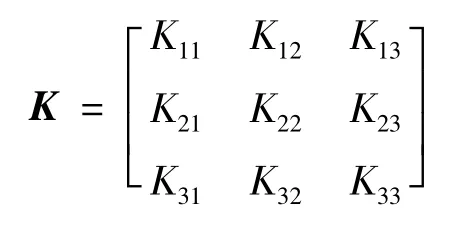
刚度矩阵的各元素表示为:

这里亦可利用振型叠加法［11］求解方程。

3 模型突变过程及仿真结果

3.1 突变过程

振动筛在稳定运动的情况下因弹簧故障引起系统力学模型突变，此瞬间过程可认为系统的状态参数如位移(角位移)、速度(角速度)等不发生变化［8－10］。基于这个特点，可以将模型突变前系统末状态作为突变后系统的初始状态，通过上述振型叠加法求出产生突变的多自由度系统的时域响应特性。

图5表明了直线筛力学模型因弹簧故障而向自由度更多的方向突变的过程，其中C指代系统状态参数的集合。t0～t1时间段内系统以传统单自由度(1－DOF)模型振动，t0时刻的状态定义为C10、t1时刻的状态定义为C1t;t1～t2时间段内系统表现为突变二自由度(2－DOF)模型，初始状态为 C20、末状态为 C2t，很明显，C20=C1t;同理，系统在t2～t3时间段内可描述为突变三自由度(3－DOF)模型，其初始状态即为2－DOF模型的末状态，即C30=C2t。表2列出了直线筛力学模型向自由度增多方向单向突变的可行路线。

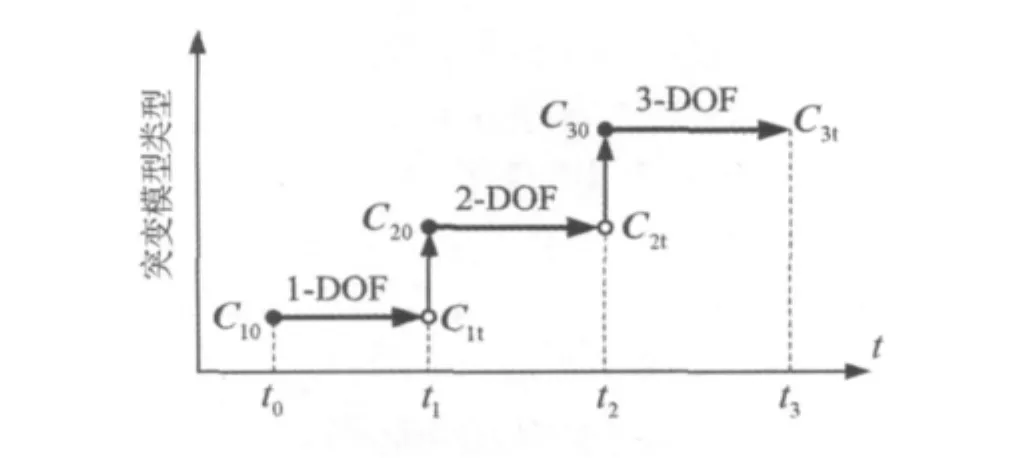
图5 模型向更多自由度单向突变的过程Fig.5 Catastrophic process for more degrees of freedom of the models

表2 模型向更多自由度单向突变的可行路线Tab.2 Workable routes of the catastrophe for more degrees of freedom of the model

需要指出的是，健康状况下的直线筛在弹簧刚度变化的过程中，其自由度个数变化的可能性有很多种，可以朝自由度增多或减少的方向单向突变，也可以向两个方向混合突变，因此这个过程可能是一个混沌的过程。考虑到振动筛实际工作情况，这里只分析其力学模型向多自由度增加的方向单向突变的时间历程。

3.2 突变过程仿真

这里以现有的直线振动筛实验模拟机为例，并利用Matlab软件对模型突变过程中振动筛振动输出进行仿真模拟。该振动筛的筛面尺寸 a=0.796 m，b1=0.429 m，b2=0.296 m，振动筛总质量 m=219.8 kg，绕x轴的转动惯量Jx=16.67 kg·m2，绕y轴的转动惯量Jy=23.88 kg·m2，最大激振力 f=5 000 N，激振电机角速度ω=104.72 rad/s。弹簧初始为健康状态，刚度值k1=k2=k3=k4=31 210 N/m;令故障弹簧刚度值均为25 260 N/m，并保持不变。根据以上物理参数，可以计算:弹簧无故障时，单自由度直线筛系统的固有频率为23.83 rad/s;故障下突变二自由度系统的二阶固有频率分别为20.25 rad/s和27.75 rad/s;故障下突变三自由度系统的三阶固有频率依次为20.23 rad/s、26.19 rad/s和32.08 rad/s，此时振动筛在远共振区工作。其力学模型向自由度增多方向单向突变的时间历程中，质心处筛面沿z轴方向的位移，以及绕y轴、x轴方向的角位移的仿真结果如图6～图9所示(图中“·”指代突变位置)。

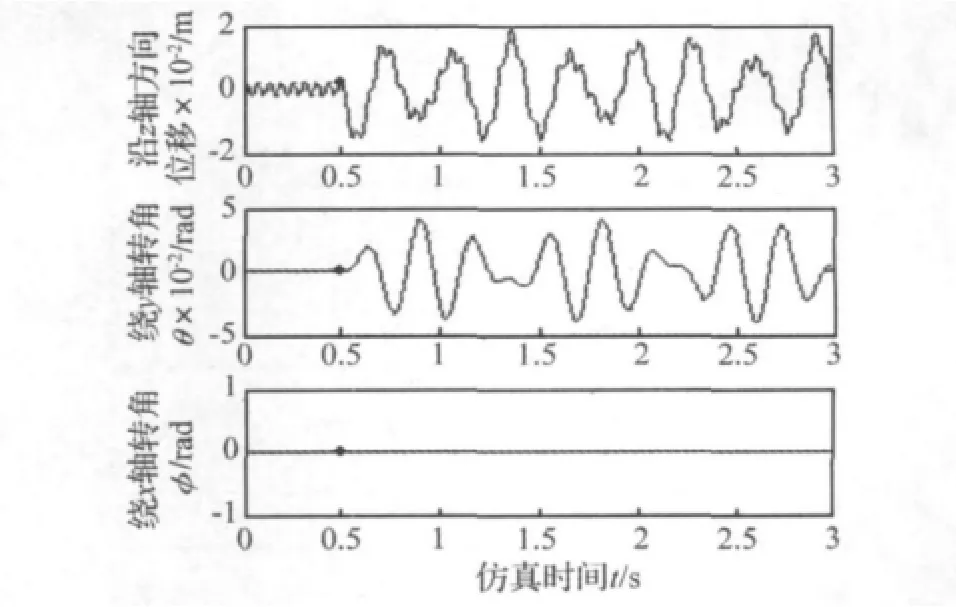
图6 1－DOF→2－DOF突变过程Fig.6 Catastrophic process from 1－DOF to 2－DOF model

图6给出了0～3 s时间段内，直线筛从单自由度运动向二自由度(k1=k2=25 260 N/m，k3=k4=31 210 N/m)运动突变的过程，其中突变发生在t=0.5 s时刻。发生故障后，z方向向上弹簧的总刚度减小，相同的激振器能量输入时，为维持系统能量守恒，弹簧变形应更大，表现为竖直方向的振动加强;另外，由于自由度变化引起了筛面绕y轴的运动分量的产生，时间历程曲线表现出从无到有的变化。该过程中筛面绕x轴的转角φ始终为零，即筛面不包含该分运动。

图7给出了0～3 s时间段内，直线筛从单自由度运动直接向三自由度(k1=k2=k3=25 260 N/m，k4=31 210 N/m)运动突变的过程，其中突变发生在t=0.8 s时刻。同样，随着自由度数的增大，系统振动加强。而三自由度情况下，由于其三阶固有频率相近，再利用振型叠加法时，其简谐振动合成的振动表现出类似拍振现象。

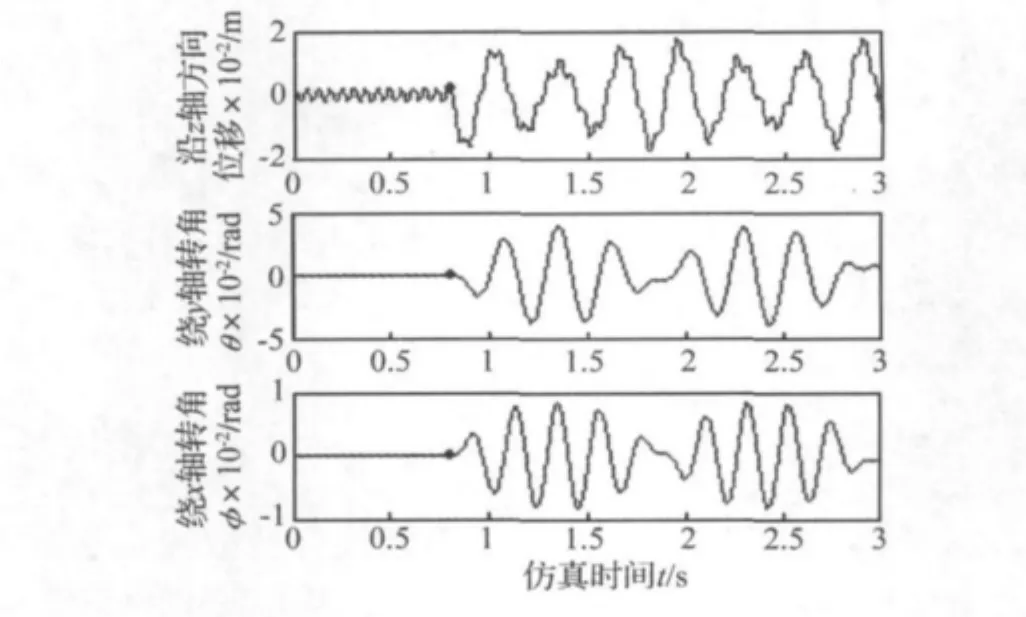
图7 1－DOF→3－DOF突变过程Fig.7 Catastrophic process from 1－DOF to 3－DOF model

图8给出了0～3 s时间段内，直线筛从二自由度(k1=k2=25 260 N/m，k3=k4=31 210 N/m)运动向三自由度(k1=k2=k3=25 260 N/m，k4=31 210 N/m)运动突变的过程，其中突变发生在t=0.9 s时刻。系统竖直方向上的振动及绕y轴转动的表现形式几乎不变，但是绕x轴转动从无到有，突变明显，且仍表现为类似拍振现象。

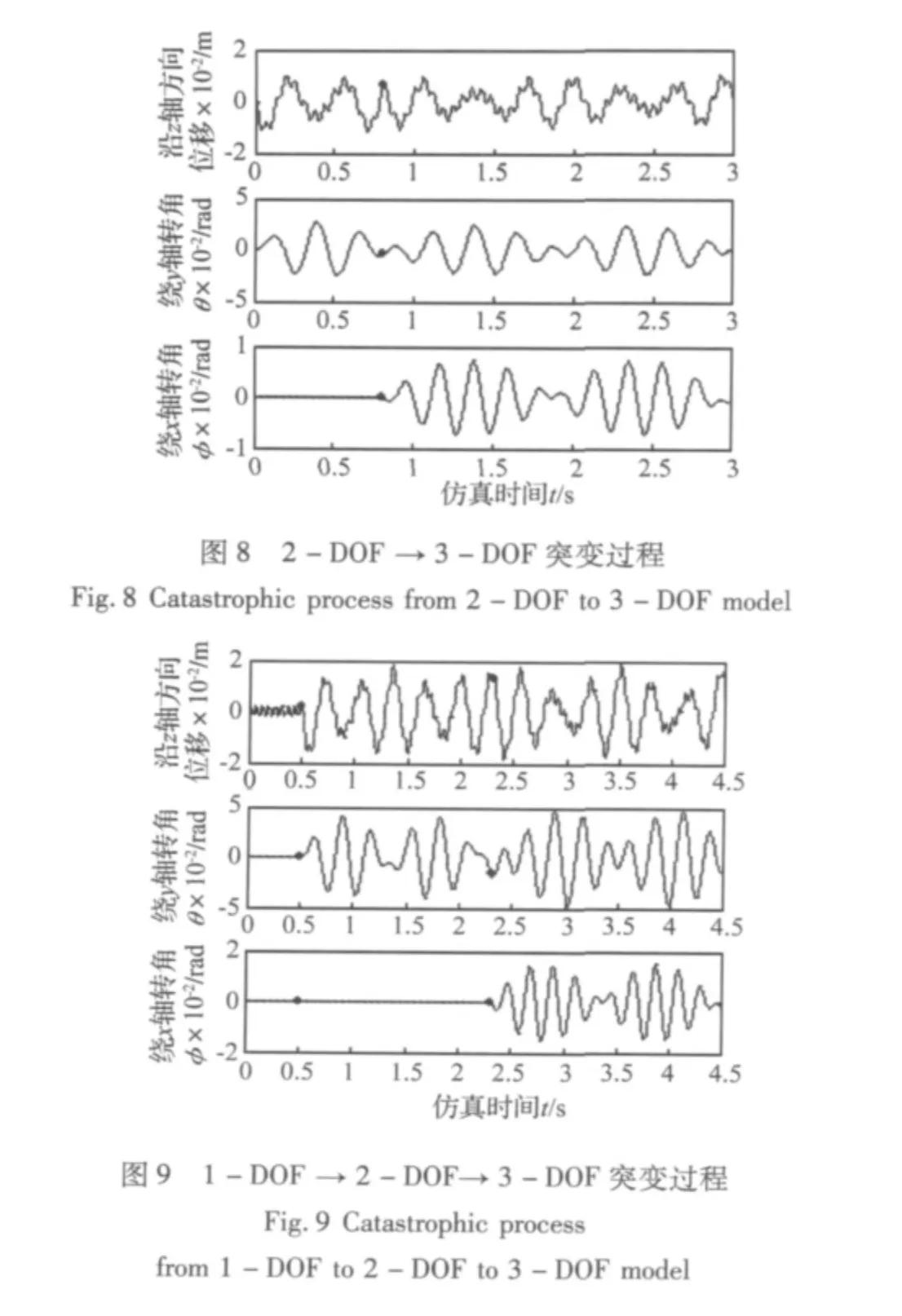
图9给出了0～4.5 s时间段内，直线筛从健康状态下的单自由度运动依次向二自由度(k1=k2=25 260 N/m，k3=k4=31 210 N/m)运动、三自由度(k1=k2=k3=25 260 N/m，k4=31 210 N/m)运动突变的过程，两次突变分别发生在t1=0.5 s，t2=2.3 s时刻。系统竖直方向上的振动及绕y轴转动类似简谐振动，而绕x轴转动从无到有，突变明显，且仍表现为类似拍振现象。

4 结论

本文在对直线筛振动系统因减震弹簧故障而引起的力学特性突变定性分析的基础上，从传统的弹簧健康状态的单自由度模型出发，分别建立了两种适合表征弹簧故障下的直线筛多自由度力学模型;分析了其突变过程，并利用模型突变瞬间系统状态参数不变的特点，对系统的力学突变过程中的系统响应进行了数值仿真;弹簧故障下直线筛二自由度、三自由度力学模型的建立及其振动微分方程的推导，以及时间历程上直线筛弹簧故障时表现出的振动加速度响应加强及类似拍振等特性，为时域内直线筛系统的状态监测与故障诊断提供了一定的理论依据。

［1］ Steyn J.Fatigue failure of deck support beams on a vibrating screen［J］.International Journal of Pressure Vessels and Piping，1995，61(2－3):315－327.

［2］ Xue G H，Zhao G R，Wu S Y.Transfer function law and diagnosis method of large vibrating screen lower beam with crack flaw［C］.2011 Third International Conference on Measuring Technology and Mechatronics Automation(ICMTMA)，2011:1044－1047.

［3］ 尹忠俊，刘建平，赵专东.交变载荷作用下大型振动筛的应力分析［J］.天津大学学报，2007，40(11):1363－1366.

［4］ 贺孝梅，刘初升，张成勇.基于多频约束和解析灵敏度法的大型振动筛优化设计［J］.中南大学学报(自然科学版)，2011，42(3):664－670.

［5］ 雷 红.振动筛减振弹簧屡次损坏的原因及处理方法［J］.化工矿物与加工，2007(8):39－39.

［6］ Winthrop M F，Baker W P，Cobb R G.A variable stiffness device selection and design tool for lightly damped structures［J］.Journal of Sound and Vibration，2005，287(4－5):667－682.

［7］ 彭利平，刘初升.3自由度振动筛动力学建模及固有频率分析［J］.机械设计，2011，28(8):50－53.

［8］ 王宗勇，龚 斌，闻邦椿.刚度与阻尼突变转子系统的动力学研究［J］.振动与冲击，2008，27(4):73－77.

［9］ 刘树英，宋雪萍，闻邦椿.转子系统故障发展过程的突变［J］.东北大学学报(自然科学版)，2005，26(3):285－288.

［10］ Ramaratnam A，Jalili N.A switched stiffness approach for structural vibration control:theory and real-time implementation［J］.Journal of Sound and Vibration，2006，291(1－2):258－274.

［11］ Singiresu S R，著.李欣业，张明路，译.机械振动(第四版)［M］.北京:清华大学出版社，2009.