迎爆加强筋耦合程度及简化建模方式的研究
李 聪,张世联,刘慧泉,武少波
(上海交通大学 船舶海洋与建筑工程学院,上海 200240)
在舱内爆炸载荷作用下,舱段结构会产生塑性大变形甚至破口,最终可能导致舱段的断裂或船体梁崩溃,为此研究舱内爆炸载荷对舱段结构的破坏效应显得尤为重要。
在舰船结构的防爆计算分析中,通常采用非线性有限元数值分析方法。对舱内处于迎爆状态的加强筋,为了能够得到较为准确的爆炸载荷作用下结构的响应,MSC.Dytran分析软件要求将参与流固耦合的加强筋建入封闭耦合面内[1]。考虑到舱内迎爆加强筋数目众多,全部耦合会增加大量建模工作量及计算时间,本文旨在探讨一种能保证一定精度且耦合程度尽量低的简化建模方式,以提高工作效率。
目前,国内外有许多学者在爆炸载荷作用下结构响应的领域内进行了深入的研究,通过理论计算[2-3]、试验[4]以及数值模拟[5-6]等方式对板格响应进行分析,但对迎爆加强筋的研究较少;梅志远等[7]在船用加筋板架爆炸载荷下动态响应数值分析中,对一迎爆加强筋进行了耦合计算,并通过与试验值的对比验证了MSC.Dytran流固耦合算法的可靠性,但没有充分讨论耦合程度对响应和计算效率的影响;另外,在对舰船舱室内部以及舷侧防爆结构内部爆炸的数值模拟中[8-9],大多以纯板组成的舱段为研究模型,也没有考虑加强筋耦合的影响。
由于目前关于迎爆加强筋耦合程度不同对结构响应影响的研究尚未见报道,为此本文基于MSC.Dytran分析软件,针对一局部甲板板架,对迎爆的加强筋进行了不同程度的耦合建模,计算分析其耦合程度对局部板架响应的影响。研究结果表明:在满足一定的响应精度条件下,对迎爆加强筋寻找一种适用且简单的耦合,可以减少舱内爆炸有限元模型建模工作量并提高模型计算分析的效率。
1 迎爆加筋板架有限元模型
迎爆加筋板架模型为一简化的纵骨架式甲板局部板架,其中:纵骨间距400 mm,纵桁间距2 m,强横梁间距1.5 m;甲板板厚10 mm,纵骨为Γ10号球扁钢,纵桁为腹板360×12 mm2、面板200×16 mm2的T型材。
为了研究甲板结构中主要构件和次要构件在迎爆状态下耦合程度不同时对结构响应的影响,选择纵桁和强横梁之间的“甲板-纵骨”板架和含有两根纵桁的“甲板-纵骨-纵桁”板架为对象,其有限元模型分别如图1与图2所示,耦合形式分别如图3和图4所示。
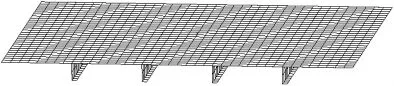
图1 “甲板-纵骨”有限元模型Fig.1 “Deck-longitudinal”FE model
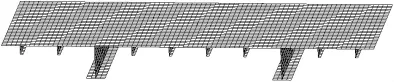
图2 “甲板-纵骨-纵桁”有限元模型Fig.2 “Deck-longitudinal-girder”FE model
图3 为型材在四种耦合程度下的甲板-纵骨模型,封闭耦合面由拉格朗日单元与哑元[1]构成,四根纵骨由左向右编号为1-4。为了分析纵骨计入耦合面程度对板架响应的影响,在模式Ⅰ中,甲板板、纵骨的腹板和小翼板均建入了耦合面,空间被划分为六个欧拉域,该模式为精确建模方式;在模式Ⅱ中,只有甲板板建入了耦合面,空间被划分为两个欧拉域;在模式Ⅲ中,甲板板和纵骨腹板建入了耦合面,空间被划分为六个欧拉域;在模式Ⅳ中,甲板板和纵骨小翼板建入了耦合面,空间被划分为两个欧拉域。

图3 纵骨在四种耦合程度下加筋板架示意图Fig.3 Schematic view of stiffened grillage’s with longitudinal in four kinds of coupling degrees

图4 纵骨及纵桁在四种耦合程度下加筋板架示意图Fig.4 Schematic view of stiffened grillage’s with longitudinal and girder in four kinds of coupling degrees
图4 为型材在四种耦合程度下含有两根纵桁的甲板局部板架有限元模型(下称甲板-纵骨-纵桁模型),八根纵骨由左向右编号为1~8,两根纵桁由左向右编号为1~2。在模式Ⅰ中,甲板板、纵骨的腹板和小翼板、纵桁的腹板和小翼板均建入了耦合面,空间被划分为12个欧拉域,该模式为精确建模方式;在模式Ⅱ中,甲板板以及纵骨的小翼板建入了耦合面,空间被划分为2个欧拉域;在模式Ⅲ中,甲板板、纵骨的小翼板和纵桁的小翼板建入了耦合面,空间被划分为2个欧拉域;在模式Ⅳ中,甲板板、纵骨小翼板、纵桁的腹板和小翼板建入了耦合面,空间被划分为4个欧拉域。
图1和图2两模型装药位置均位于板中心点下方1.5 m处,用三维欧拉单元模拟空气,气体的状态方程采用Gamma律状态方程,即:
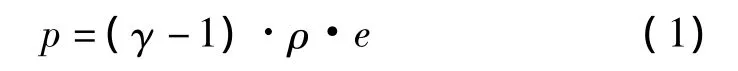
式中:比热比 γ =1.4、空气密度 ρ=1.25 kg/m3、空气比内能 e=2.1 ×105J/kg。
TNT炸药用高能高压的空气来模拟,亦采用Gamma律状态方程,其中炸药密度ρd=1 600 kg/m3,炸药比内能 ed=4.2 ×106J/kg。
结构材料的应力-应变关系近似的模拟为双线性弹塑性材料,屈服强度440 MPa,弹性模量210 GPa,泊松比0.3,硬化模量 4 GPa,最大塑性应变 0.25。材料采用能考虑动态应变效应的Cowper-Symonds模型,同时考虑材料应变强化效应,其本构方程如下:
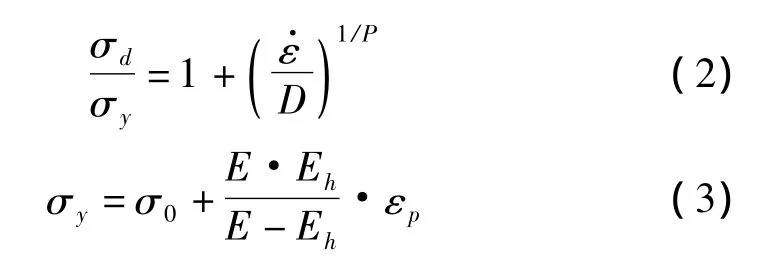
式中:σd为动态应力、σ0为初始屈服极限、ε·为等效应变率、D和P为材料常数(本文中分别取为40.5和5)、E为弹性模量、Eh为硬化模量、εp为等效塑形应变。
对文中模型的简化有以下几点说明:第一,模型的边界条件均假定为刚性固定。由于本文目的不是准确的求解某一板架的响应,而在于对比耦合程度不同对结构响应的影响,因此本文选取了一种典型的边界条件来研究,在保证所对比模型的边界条件相同的基础上得到的结论有一定的代表性;第二,没有考虑结构重力的影响,是因为重力相对于爆炸冲击载荷来说为高阶小量,可以忽略不计;第三,没有考虑结构阻尼的影响,是因为结构阻尼对能量的消耗是一个随时间相关的量,但本文仅研究起爆后0.005 s内结构的响应,因此结构阻尼的影响亦可以忽略不计。
2 耦合程度不同时局部板架模型计算结果分析
基于MSC.Dytran分析软件,以甲板垂向变形为响应输出,对两种局部板架模型进行了计算,其中甲板-纵骨模型采用40 kg的TNT炸药量,而甲板-纵骨-纵桁模型由于更接近于真实甲板板架结构,故选取了40 kg、60 kg和80 kg三种TNT炸药量。计算得到了迎爆状态下加筋板架在耦合程度不同时的结构响应值,并对其进行了分析。
2.1 甲板-纵骨模型
对于该甲板-纵骨模型在耦合程度不同时的响应特性,表1给出了1号纵骨和2号纵骨与甲板板相交线中点以及甲板板中心处的最大垂向变形值,图5给出了上述三个参考点处垂向变形的时历曲线。图6给出了爆炸后0.003 s时刻四种耦合程度下的板架横截面变形。
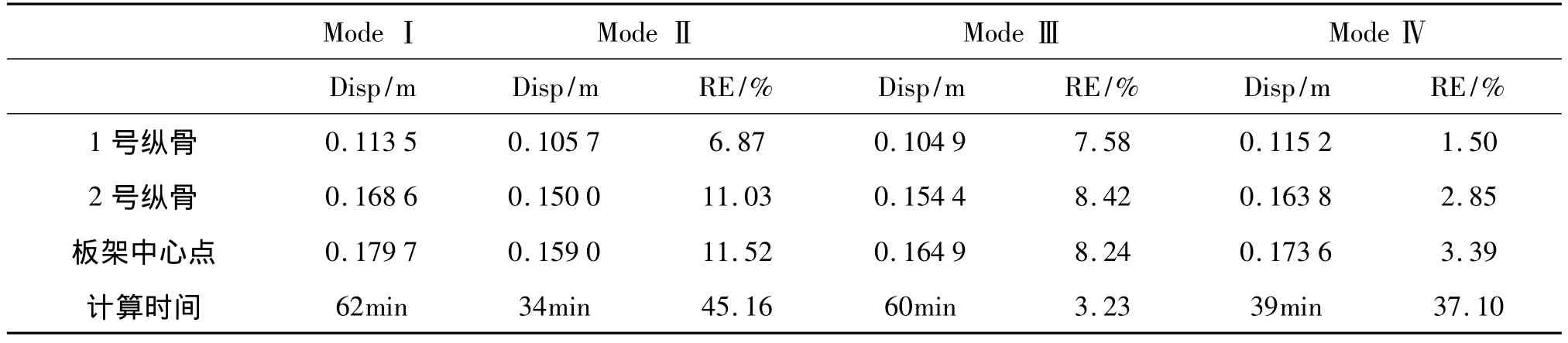
表1 甲板-纵骨模型在四种耦合程度下的最大垂向变形Tab.1 Maximum vertical displacement of“deck-longitudinal”model in four coupling degrees
从表1中可以看出,模式Ⅱ至模式Ⅳ与模式Ⅰ相比,各点最大垂向变形的相对误差分别为REⅡ≈6% ~12%,REⅢ≈7% ~9%,REⅣ≈1% ~4%。数据表明,将加强筋计入耦合面可以增大板架变形,原因有两点:一是腹板产生侧向塑性变形,降低了加强筋及板架整体的抗弯强度;二是小翼板接受冲击波作用,增加板架整体受力。表1中模式Ⅲ以及模式Ⅳ的数据证实了上述分析,同时说明小翼板对板架变形的贡献大于腹板的贡献。Henrych给出了冲击波峰值超压的经验计算公式[10]:
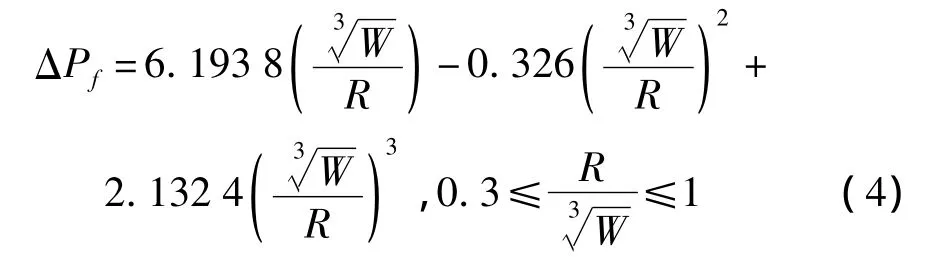
式中:ΔPf为峰值超压(kg/cm3),R为考察点距爆炸中心距离(m),W为炸药重量(kg)。对于本算例,可粗略估算单个板格在小翼板计入耦合面后,所受到的冲击力增加了:
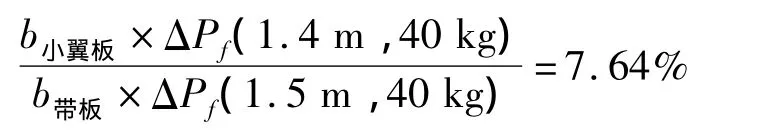
而表1中模式Ⅳ各点位移相对模式Ⅱ增幅均约为9%,从理论上解释了小翼板参与耦合可以有效减小误差的原因。综合分析精度与计算效率,模式Ⅱ对计算时间的提升最大,但精度却最低;模式Ⅲ几乎没有提升计算效率,精度也较低,其对计算效率没有影响的原因在于欧拉域的个数与精确模型相同,计算量基本无改变;模式Ⅳ对效率的提高虽不及模式Ⅱ,但亦达到了37%,同时精度也得到有效的提升。因此在下一节对甲板-纵骨-纵桁板架的分析中,纵骨均采用仅耦合小翼板的方式。
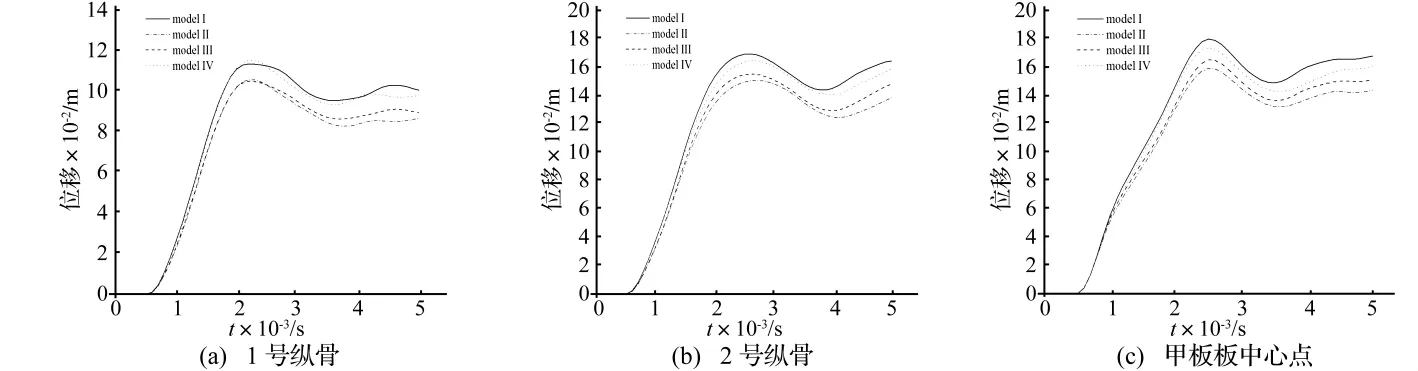
图5 甲板-纵骨模型中三个参考点处的垂向位移时历曲线Fig.5 Vertical displacement time history of three reference points in“deck - longitudinal”model

图6 四种耦合程度下甲板-纵骨模型变形图Fig.6 Deformation pattern of“deck-longitudinal”model in four coupling degrees
从图5可以看出四种耦合程度下甲板-纵骨模型板架变形随时间变化的趋势基本一致,但变形大小有所不同。另外如图6所示,模式Ⅱ与模式Ⅳ这两种简化模型的变形模式基本相同,但与精确模型(模式Ⅰ)相比,纵骨变形模式以及板架产生最大变形的位置均不同,这主要是由于模式Ⅱ和模式Ⅳ没有把纵骨腹板建入耦合面,纵骨仅随甲板弯曲而产生小量的侧向变形。模式Ⅲ由于腹板计入了耦合面,与模式Ⅰ纵骨变形模式较为相近。四种耦合程度下板架总体变形模式基本相同。
2.2 甲板-纵骨-纵桁模型
对于该甲板-纵骨-纵桁模型在耦合程度不同时的响应特性,表2给出了三种不同炸药量下纵桁与甲板板相交线中点以及甲板板中心处的最大变形,图7给出了该模型上述两参考点在40 kgTNT炸药量下垂向变形的时历曲线。图8给出了爆炸后0.003 s时刻四种耦合程度下的板架横截面变形。
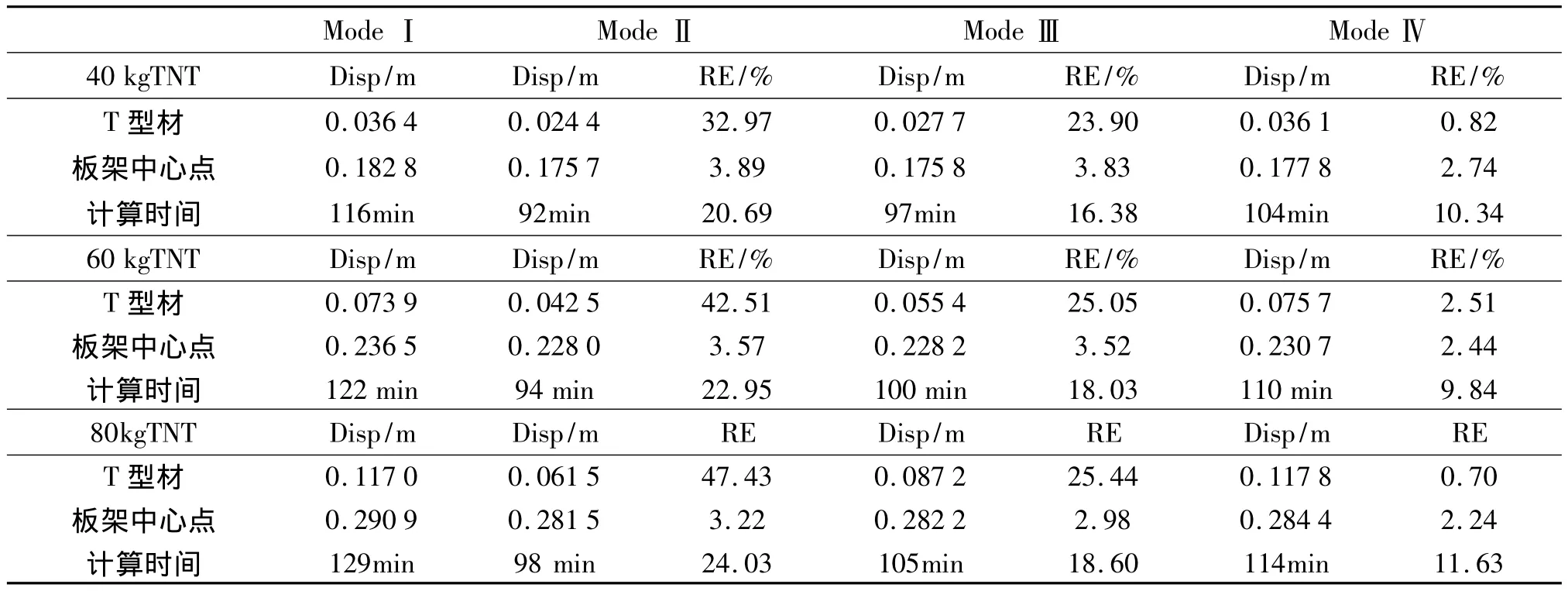
表2 甲板-纵骨-纵桁模型在四种耦合程度下的最大变形Tab.2 Maximum vertical displacement of“deck-longitudinal-girder”model in four coupling degrees
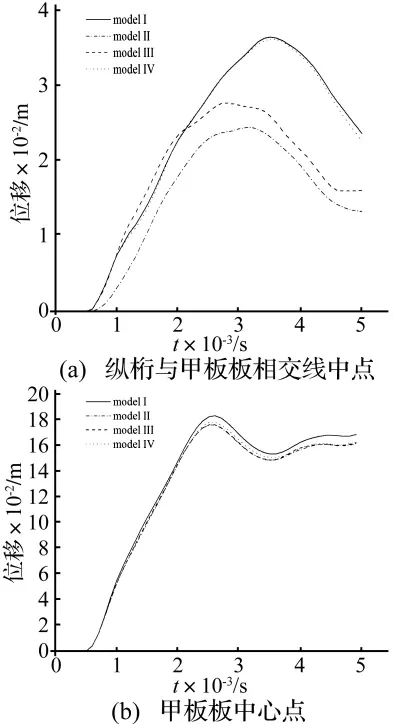
图7 甲板-纵骨-纵桁模型板架两参考点处的垂向变形时历曲线Fig.7 Vertical displacement time history of two reference points in“deck-longitudinal-girder”model

图8 四种耦合程度下甲板-纵骨-纵桁模型变形图Fig.8 Deformation pattern of“deck-longitudinalgirder”model in four coupling degrees
从表2可以看出,对于甲板中点变形,模式Ⅱ~Ⅳ的相对误差均较小,RE≈3% ~4%;而对于两根纵桁,模式Ⅱ与模式Ⅲ的结果不理想,误差较大,模式Ⅳ中相对误差REⅣ≈1% ~3%,原因分析与上节相同。
计算结果表明,迎爆局部板架的纵桁的耦合程度强弱会严重影响计算结果的精度,模式Ⅱ和模式Ⅲ虽然可减少20%左右的计算时间,但误差过大,因此必须将纵桁完整的建入耦合面,即模式Ⅳ,同时由于纵骨耦合程度较低,在减少建模工作量的同时,模式Ⅳ的计算时间仍可减少10%左右。
从图7中可以看出,对于甲板板中心,四种模式下其垂向变形随时间的变化趋势基本一致,而对于纵桁与甲板板相交线中点,模式Ⅱ与模式Ⅲ的垂向位移峰值先于模式Ⅰ和模式Ⅳ到达,而模式Ⅰ和模式Ⅳ的变化趋势则较为吻合。另外如图8所示,由于没有考虑纵桁腹板的耦合,模式Ⅱ与模式Ⅲ这两种简化模型纵桁的变形模式与精确模型(模式Ⅰ)相比均不同,基本没有侧向变形;同时模式Ⅱ至模式Ⅳ均没有将纵骨腹板建入耦合面,因此纵骨仅随甲板弯曲而产生小量的侧向变形,与模式Ⅰ有所差别。四种耦合程度下板架总体变形模式基本相同。
3 结论
本文基于MSC.Dytran分析软件,计算分析了两种甲板局部板架纵向加强筋在迎爆状态下耦合程度不同对结构响应的影响,并与全耦合模型相比,得到了一些耦合程度低但精度影响不大的建模方式,现归纳如下:
(1)对于小型加强筋(如纵骨),若不将小翼板建入耦合面,即模式Ⅱ和模式Ⅲ,会产生一定程度的误差,若将小翼板建入耦合面,即模式Ⅳ,可以有效的降低误差,并且有效减少EULER域的个数,减少建模的工作量;
(2)对于大型加强筋(如纵桁),必须将腹板和小翼板全部建入耦合面,即模式Ⅳ,否则会产生较大误差;
(3)若研究对象为加强筋的变形模式而不是板架变形的大小,则简化建模方式都会失真,需要采用精确建模方式,即模式Ⅰ。
由于文中计算结果分析均基于给定尺寸的甲板结构,建议在进行舱段模型内部爆炸计算分析前,可先选取该模型部分板架做类似的试算及综合分析。在满足一定计算精度的条件下,降低模型中加强筋的耦合程度,以减小建模工作量并提高计算效率。
[1]丁沛然,钱 纯.非线性瞬态动力学分析MSC.Dytran理论及应用[M].北京:科学出版社,2006.
[2]刘敬喜,刘 尧,汤皓泉,等.爆炸载荷作用下单向加筋方板的大挠度塑性动力响应分析[J].振动与冲击,2011,30(4):182-187.LIU Jing-xi,LIU Yao,TANG Hao-quan,et al.Plastic and large deflection dynamic response analysis of a one way stiffened square plate subjected to blast loads[J].Journal of Vibration and Shock,2011,30(4):182 -187.
[3]Cloete T J,Nurick G N,Palmer R N.The deformation and shear failure of peripherally clamped centrally supported blast loaded circular plates[J].International Journal of Impact Engineering,2005,32(1):92-117.
[4]Chung Kim Y S,Nurick G N.Experimental and numerical studies on the response of quadrangular stiffened plates.Part I:subjected to uniform blast load[J].International Journal of Impact Engineering,2005,31(1):55-83.
[5]侯海量,朱 锡,古美邦.爆炸载荷作用下加筋板的失效模式分析及结构优化设计[J].爆炸与冲击,2007,27(1):26-33.HOU Hai-liang,ZHU Xi,GU Mei-bang.Study on failure mode of stiffened plate and optimized design of structure subjected to blast load[J].Explosion and Shock Waves,2007,27(1):26-33.
[6]Kadid A.Stiffened plates subjected to uniform blast loading[J].Journal of Civil Engineering and Management,2008,14(3):155-161.
[7]梅志远,朱 锡,刘润泉.船用加筋板架爆炸载荷下动态响应数值分析[J].爆炸与冲击,2004,24(1):80-84.MEI Zhi-yuan,ZHU Xi,LIU Run-quan.Dynamic response researches of ship’s stiffened plate structure under explosive load[J].Explosion and Shock Waves,2004,24(1):80 -84.
[8]孔祥韶,吴卫国,李晓彬,等.舰船舱室内部爆炸的数值模拟研究[J].中国舰船研究,2009,4(4):7-11.KONG Xiang-shao, WU Wei-guo, LIXiao-bin, etal.Numerical simulation of cabin structure under inner explosion[J].Chinese Journal of Ship Research,2009,4(4):7-11.
[9]Du Z P,Li X B,Xia L J.Numerical simulation of warship broadside protective structure rupture under inner explosion[J].Journal of Ship Mechanics,2007,11(3):453 -461.
[10]李翼祺,马素贞.爆炸力学[M].北京:科学出版社,1992.

