柔性基础主动隔振系统的缩聚建模和时滞问题研究

宋 攀，董兴建，孟 光

(上海交通大学 机械系统与振动国家重点实验室，上海 200240)

浮筏装置是一个集多种动力学元件为一体的混合动力学系统，其结构紧凑，附加质量少，隔振效果好，且具有良好的抗冲性能。随着现代浮筏装置向大型化和轻型化方向的发展，浮筏结构设计有以下不足之处，首先在现有的分析设计过程中假定筏架和基础是刚性的，忽略了振动过程中产生的弹性变形;其次，上述浮筏隔振装置的实质是一种振动被动控制技术，对超低频振动和宽带随机振动的隔振效果并不理想。为了进一步提高舰艇的声隐身性能，有必要在浮筏隔振装置中引入作动器，然而传感器信号的采集、传输和作动器的作动过程等都不可避免的存在时滞现象。力学工作者在主动隔振研究中采用了很多控制理论中的成熟方法[1－2]，如特征结构配置方法，自适应控制，H∞控制[3－4]。在建立了反映系统力学本质的数学模型之后，对其实施振动主动控制就不存在理论上的特殊性。但是对于主动隔振系统中的时滞现象以及时滞对控制效果的影响，目前尚没有文献报导。以往人们为了理论分析和控制器设计的方便，总是忽略时滞，但即使是小时滞量也可能会导致在系统不需要能量时向其输入能量，进而引起控制效率的下降，甚至控制系统失稳。另外，我们发现，全模型最优控制需要测出受控对象的所有状态参数，而对于大型浮筏这样的复杂结构，其状态参数通常很多，这必然导致测试和在线数据处理的工作量很大，使得时滞效应变得非常明显，严重影响控制效果。而现有的浮筏隔振装置的建模方法，即多刚体法、波分析法[5]，又往往只考虑结构的刚性而忽略弹性。有限元法虽然理论上可适用于任意复杂的结构，然而，为了保证计算精度，有限元模型必然会很大，给进一步的动力分析带来很大不便。

为了解决以上技术难题，本文以浮筏装置为研究对象，针对其建模问题和时滞主动控制问题进行研究。考虑中间质量的柔性和基础的弹性，建立复杂柔性主动隔振系统模型，并通过把装置中弹性体的有限元模型在物理空间中进行减缩，建立各自的超单元，然后在把这些超单元与装置中的其它结构一起建立总体模型;将主动隔振的思想引入浮筏隔振系统，并率先在主动隔振系统中考虑作动器的时滞效应，将时滞连续控制系统离散为形式上不包含有时滞的标准离散形式，然后按照离散最优控制方法进行控制设计。因最优离散控制律直接从时滞微分方程中得出，且推导中无近似处理和估计，因此该方法易于保证控制系统的性能和稳定性。

1 基本理论

1.1 柔性耦合系统超单元缩聚[6]

假设任意结构的无阻尼动力学方程为:

通常来说，保留自由度应包括有外载荷作用的自由度、给定位移的自由度、与其它单元连接的节点自由度和要考察的自由度等，因此式(2)中的Fd应为零向量。把式(2)中的第二式展开，有:

在式(3)中，由于括号中的第一和第二项均不与xh成线性关系，因此很难直接从该式中求得xd与xh的关系矩阵。为此假定:

则有:

显然，Xd和Xh之间的关系矩阵R(0)忽略了式(3)中惯性力的影响，故该矩阵只有在静态时才是精确的，而对于动力学问题必然存在误差。构造n×k阶坐标转换矩阵P(0)为:

其中:I为k×k阶单位矩阵。假定与此结构对应的超单元的刚度矩阵和质量矩阵分别为和则有:

相应地该超单元的自由振动方程为:

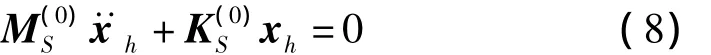
式(8)即为经典超单元法，此处的保留自由度即超单元的自由度是事先给定的，不能进行优化，这必然使得关系矩阵R(0)的精度很低。相应地，建立在该基础上的超单元的刚度矩阵和质量矩阵也存在很大的误差，且随着振动频率的增加，该误差越来越大。为了解决该问题，对前面给出的关系矩阵零阶近似R(0)进行修正。从式(8)可得:

考虑到式(5)、式(9)和式(3)，并整理可得:

从式(10)可得关系矩阵的第一次近似值:

1.2 线性时滞系统的标准离散状态方程

考虑如下n自由度的结构模型:

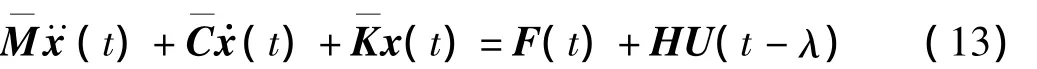
其中:x(t)∈Rn是基础、筏架和质量块的绝对位移;M分别是系统经超单元缩聚后的质量，阻尼和刚度矩阵;U(t－λ)∈Rr为控制力向量;λ为时滞量为控制力位置矩阵;F(t)为外激励载荷。假定时滞量λ可描述为如下形式:

其中:

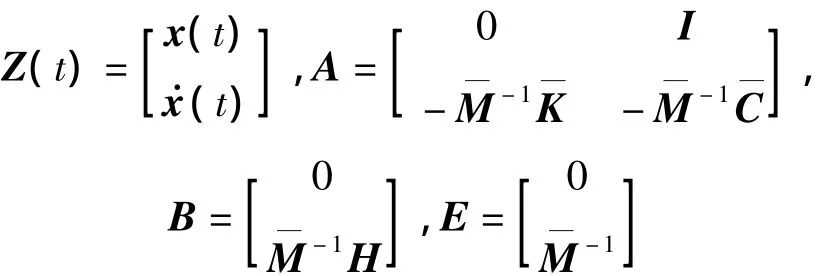
设在连接的控制对象和控制器间有一零阶保持器连接，即:

式(16)表明，作动器在相邻两个采样点间按常值对系统施加控制力。U(k)实际上代表第k步控制U(kT)，为表达方便文中其他变量表达同此。

考虑到时滞量不一定为采样周期的整数倍，将状态空间变为离散形式:

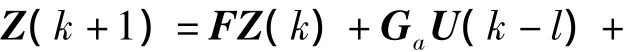
1.3 控制律的设计

按照最优控制设计方法，当进行最优控制设计时，可不考虑外部激励项。对于如下线性离散定常系统

给定二次型性能指标函数为:

其中:Q是非负定对称阵，R是正定对称阵。设S(k)是如下离散Riccatik)差分方程的解:

对于任何非负定对称阵Q0有:

存在，且S是与Q0无关的常数阵。而且，S是如下离散Riccati代数方程:

的唯一正定对称阵。则稳态控制律可表达如下:

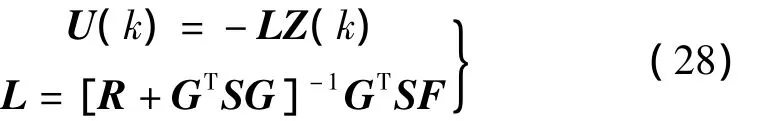
此控制律可使式(24)所示的性能指标函数Jd极小。

因为式(24)所示的性能指标函数只能够保证系统采样点上具有好的响应性能，不能保证系统在采样点也具有良好的响应性能，甚至可能在采样点间隐藏着振荡现象。为使系统具有令人满意的连续响应性能，目标函数取连续的二次型函数将能反应实际系统的性能要求。因此，考虑如下连续二次型目标函数:

式(29)可进一步表示为:

其中:

因此，现在问题变为对式(19)所示的离散状态方程，寻求最优控制式所示的性能指标Jc极小，从而可以采用式(23)～式(28)所示的方法进行求解，最优控制可表达为:

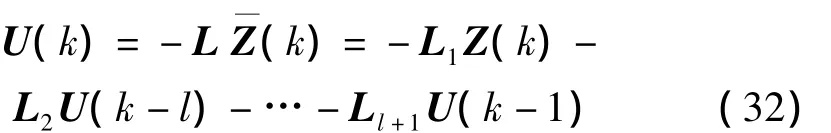
其中:L1～Ll+1分别是L的相应维数的分块矩阵，由式(32)可见，此时的最优控制除直接的线性反馈外，还包含前l拍控制量的线性组合。

2 数值分析

图1给出了一浮筏装置的简化模型[6]，m1=100 kg和m2=120 kg表示被隔振机械;筏A架与基础B的尺寸分别为1.2 m ×0.8 m ×0.02 m 和2.8 m ×0.8 m ×0.04 m，基础B的两短边简支、两长边自由;上下两层弹簧隔振k1=1.0×105N/m，k2=5.0×105N/m，材料的弹性模量 E=2.0 ×1011N/m2，密度为 ρ=7 800 N/m3。

基于浮筏系统为对象，以降低振源引起自身及弹性基础振动幅值为目标，并假定只在如图1所示位置施加主动控制，即在板式筏架上下两层与被隔振机械对位的直线上安装四个主动隔振器。我们知道，设备放置在筏架上，浮筏基座又与壳体弹性连接。浮筏装置一方面可以减小放置在筏架上的机组扰动源自身振动，另一方面可是使柴油机和电机发出的机械噪声缓冲衰减，不能或较少传出潜艇外，达到隐身的作用。为了考察筏架上设备自身振动，以及浮筏与潜艇连接板的隔振效果，并且考虑到浮筏结构的对称性，选取如图1所示的两个目标点。激励力采用0～50 Hz的白噪声，持续时间取为20 s，采样周期取为T=0.002 s，性能指标式(24)中Q和R依据经验选取;数值计算采用四阶龙格库塔法。

图1 浮筏模型主动控制施加点与目标点示意图Fig.1 The locations of active control and the target points of the floating raft model

2.1 超单元缩聚

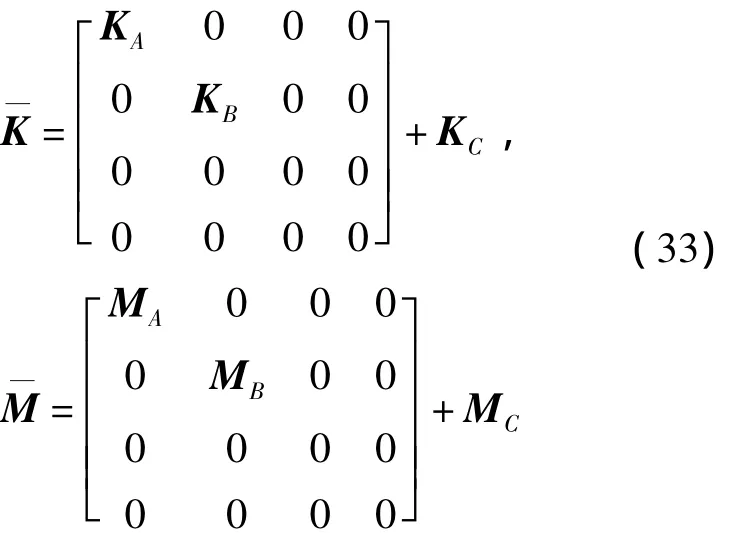
由于筏架和基础均是弹性的，因此在对该系统建模之前首先用常规方法对筏架和基础进行有限元建模。由于弹簧只有z方向的位移，因此选择图1中筏架A上与弹簧阻尼器相连的12个节点上z方向的线位移为保留自由度得到筏架超单元刚度矩阵和质量矩阵分别为KA和MA。同样，选择图1中基础B上与弹簧阻尼器相连的12个节点上Z方向的线位移为保留自由度得到的基础模型超单元的刚度矩阵和质量矩阵分别为KB和MB。将筏架和基础的超单元刚度矩阵和质量矩阵与浮筏的其它部件组装成结构的总刚度矩阵和总质量矩阵如式(33)，其中，KC和MC分别为由弹簧和机械在系统总体坐标中形成的刚度矩阵和质量矩阵。当浮筏的总体刚度矩阵和质量矩阵建立以后，就可以对其进行动态性能分析。

将完整未缩聚模型在有限元软件中所求得的系统固有频率作为精确解。表1是完整模型与降阶模型的前二十阶固有频率比较。可以看出，用本文提出的超单元建模方法建立起来的有限元降阶模型共有26个自由度，显然它比未降阶的模型小得多，而用该降阶模型求得的系统前二十阶固有频率与精确解基本吻合。

2.2 最大时滞量的确定和控制效果比较

当控制系统中不存在时滞，即λ=0时，式(29)所示的连续形式性能指标所确定的最优控制律对存在时滞的结构进行振动控制，结构各节点的峰值绝对位移和峰值控制力值随时滞量λ的变化曲线由图2所示。可以看出，结构稳定的最大允许时滞量可近似确定为λ=0.000 4 s。由此可知，控制系统中时滞问题应得到人们的足够重视，否则控制系统有可能发生不稳定现象。

当采用的是线性离散定常性能指标Jc进行控制律设计时。施加主动控制前后的系统响应对比，如图3所示。图4为结构各个目标点的峰值响应和峰值控制力随时滞λ的变化曲线，可以看出，本文所提控制方法不但较好的控制结构的峰值响应，而且即使控制系统中存在较大的时滞量，所提控制方法仍能保证控制系统的稳定性。同时，当选择合适的时滞量时能够在较小的控制代价情况下，达到更好的控制效果。

表1 完整模型频率与降阶模型频率(Hz)Tab.1 The frequency of the complete model and reduced model(Hz)

图2 用无时滞时所设计的控制律对有时滞时结构进行控制的峰值响应Fig.2 The peak response of the control system with delay controled by the control law designed for the system without time delay

图3 各目标点响应对比(λ =0.2 s，T=0.002 s)Fig.3 Comparison of the response of the target points

图4 目标点2峰值位移响应Fig.4 Curves of the peak displacement response

3 结论

本文以复杂柔性耦合主动隔振系统为对象，根据受控对象的部分状态参数对输出状态控制器进行设计，并考虑到主动隔振系统中作动器不可避免的时滞问题，通过分析，结论如下:

(1)超单元缩聚方法建立起来的降阶模型不仅在规模上远远小于未降阶的有限元模型，而且能很好地保持原系统的中、低频动态特性;

(2)通过将时滞微分方程离散化，在状态变量中增加与时滞量相关的前若干步控制项，将时滞差分方程转换成形式上不包含时滞项的标准差分方程形式，采用二次型性能指标为目标函数设计控制律。该控制方法具有良好的控制效果，即使控制系统中存在较大的时滞量，所提控制方法仍能保证控制系统的稳定性。

(3)以主动隔振系统的隔振性能为目标函数，将时滞量作为一个控制器设计参数，通过选择合适的时滞量可以在控制代价很小的情况下达到很好的控制效果。

总之，控制系统中的时滞存在潜在的利用价值，在对时滞抑制进行研究的同时，还应深入研究时滞的利用问题

[1]Chen K T，Chou C H，Chang S H，et al.Intelligent active vibration controlin an isolation platform[J].Applied Acoustics，2008，69(11):1063 －1084.

[2]Fei H Z，Zheng G T，Liu Z G.An investigation into active vibration isolation based on predictive control:Part I:Energy source control[J].Journal of Sound and Vibration，2006，296(1－2):195－208.

[3]Kerber F，Hurlebaus S，Beadle B M，et al.Control concepts for an active vibration isolation system[J].Mechanical Systems and Signal Processing，2007，21(8):3042 －3059.

[4]Hu Y R，Ng A.Active robust vibration control of flexible structures[J]. JournalofSound and Vibration，2005，288(1－2):43－56.

[5]W C J，W R G.Vibrational power transmission in a finite multi-supported beam[J].Journal of Sound and Vibration，1995，181(1):99－114.

[6]瞿祖清.结构动力缩聚技术理论与应用[M].上海:上海交通大学出版社，1998.