直升机起落架的集成计算
孙为民,徐 渊
(中国直升机设计研究所,江西景德镇,333000)
0 引言
直升机起落架在研制过程中,需要完成各种分析计算。这些计算一般包括停机状态的计算、减缩质量计算、静态性能计算及主、尾起落架各种着陆状态下的性能计算。在研制过程中,为了获得最优的设计,需要对参数进行反复调整。任何参数的调整都可能对关键性的停机状态和起落架着陆性能产生影响,因此每一个参数的调整都要进行一次全面的计算。这些计算繁复,数据量大,数据的前处理后处理多。
目前对起落架的分析通常是采用某种计算机语言进行编程计算,或者采用动力学软件(如MSC.Adams)进行分析,但这些分析计算在使用上都有一定的不便之处。采用通用的动力学软件可以较快地进行建模分析,但在计算结果上需要人工不断地提取数据。如果要进行优化,则需要人工不断地调整参数进行模型修改。另外,在复杂的缓冲器建模上通用的动力学软件也有一定的不足。采用某种计算机语言(如FORTRAN语言或C语言)进行编程计算,在数据输入输出上,需要单独编制一定格式的数据文件,这些数据文件的可读性、直观性并非最佳。在对数据结果进行图表绘制上,也常常需要借助其他软件来完成。
作为通用办公软件的Excel具有良好的数据编辑处理能力,能够方便地绘制各种图表。作为高性能数值计算软件的Matlab具有优良的编程能力,并与Excel具有良好的接口。作者将Excel作为输入输出工具,采用Matlab编制起落架的各种计算程序。这些起落架的计算程序运行时从Excel文件读入各种参数,将计算结果输出到Excel文件中。
1 输入数据
起落架的常规计算需要的数据包括整机的重量重心及转动惯量、主尾起落架的交点数据,主尾起缓冲器的数据包括充填参数及油孔数据、主尾起轮胎的压缩数据及轮胎重量外径等。建立一个Excel文件,命名为zxxcalculation.xls。在Excel里插入一个工作表命名为“所有参数”,将上述数据分别分块存储在“所有参数”这个工作表里,并加以颜色标记,以做到条理清晰、直观,如图1所示。可加注释或图片对各参数进行说明。
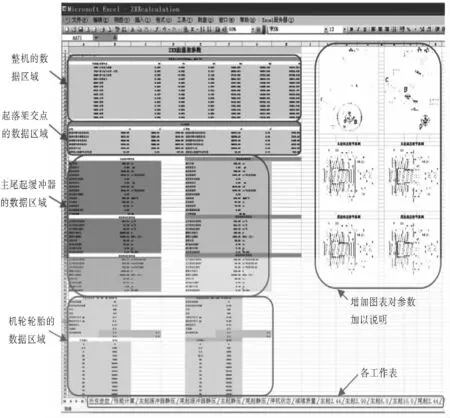
图1 工作表“所有参数”的数据编制示图
2 输出数据
起落架的常规计算包括停机状态的计算、减缩质量计算、静态性能计算(包括主尾起落架的静压曲线计算和主尾起缓冲器的静压曲线计算)、主尾起落架的着陆性能计算。在zxxcalculation.xls里插入多个工作表,分别命名为“主起缓冲器静压”、“尾起缓冲器静压”、“主起静压”、“尾起静压”、“停机状态”、“减缩质量”、“主起 2.44”、“尾起 2.44”等,以存储各种计算结果。
有些计算较为简单,输出的数据也不多。如主起缓冲器静压计算,是一个力的平衡计算,输出的数据包括缓冲器行程和缓冲器载荷,根据这两项数据即可绘制主起缓冲器静压曲线。为了结构设计及气体压力的考虑,可将高、低压腔缓冲器的活塞行程及气体压力一起输出。单独输出所需的初始点、拐点和终点的专项数据。所有这些主起缓冲器静压计算的结果按自己设定的格式存放在具体特定位置,如图2所示。
有些计算比较复杂,输出的数据较多。如主起着陆性能计算,计算的是一个动力学微分方程组,输出的数据包括轮胎垂直载荷、重心行程、缓冲器载荷、缓冲器行程、轮胎航向载荷、油液阻尼力、气体压力等。对复杂的缓冲器可能还包括高低压腔的活塞行程、高低压腔节流阀的行程等。将所有这些数据输出到某个工作表,如工作表“主起2.44”,用于存储主起2.44m/s着陆的性能计算结果。着陆性能一般包括多个状态,可增加工作表以存储不同状态的着陆性能数据如“主起2.99”、“主起 6.0”等。这些表格存储的都是详细的数据,一般需要将这些数据绘制成图表,如根据轮胎垂直载荷和重心行程绘制起落架功量图,根据缓冲器载荷和缓冲器行程绘制缓冲器功量图,而且常常是将不同着陆状态的功量图做在一个表格里。在zxxcalculation.xls里增加工作表“性能计算”,直接根据“主起2.44”、“主起2.99”等工作表里的数据绘制主起落架功量图等所需示图。在出计算报告的时候,除了示图以外,还需要列出各种数据表格,需要各单项的特殊数据如轮胎最大垂直载荷、重心最大行程、起落架吸收功量、起落架效率系数等,这些数据单独输出到工作表“性能计算”的相关数据区域即可,如图3所示。

图2 主起缓冲器数据输出示图

图3 主尾起落架着陆性能图表编制表示图
3 集成计算的程序编制
M语言是Matlab的编程语言,编制的程序是以m为后缀的文件。
对直升机起落架常规计算编制程序zxmaircurve.m、zxnaircurve.m、zxmlgcurve、zxnlgcurve.m、zxparking.m、zxmass.m、zxmlg.m、zxnlg.m 分别用于完成主起落架缓冲器的静压曲线计算、尾起落架缓冲器的静压曲线计算、主起落架的静压曲线计算、尾起落架的静压曲线计算、停机状态的计算、减缩质量计算、主起落架的着陆性能计算、尾起落架的着陆性能计算。
前面已经叙述,完成起落架常规计算所需的参数均存放在工作表“所有参数”里,因此,对应不同的计算,需要的输入数据均可从该工作表里读取。如完成主起缓冲器静压计算需要的缓冲器的参数从主起缓冲器数据区域的相应表格里读取,并存放到数组常量moleop里,如代码1,含义为从zxxcalculation.xls的“所有参数”工作表中读入单元格B35到B47的数据,赋值给moleop数组。再将这些常量一个个地赋值给常量(所有计算注意单位及转换),如代码2,含义为数组moleo的第2个参数赋值给air_lp0。完成计算后,将计算结果存储到工作表中,如代码3,含义为将计算结果缓冲器载荷Fair存储到zxxcalculation.xls的“主起缓冲器静压”工作表中的B3单元格里。
moleop=xlsread(‘zxxcalculation.xls’,‘所有参数’,‘B35:B47’); (代码1)
air_lp0=moleop(2)*1.0E6; (代码2)
xlswrite(‘zxxcalculation.xls’,Fair,‘主起缓冲器静压’,‘B3’); (代码3)
有些计算比较简单,一个主程序即可完成。有些计算较为复杂,如整机停机状态的计算,所需要的数据较多,包括整机的重量重心、主尾起落架的交点数据、主尾起缓冲器的数据、主尾起机轮轮胎数据。将这些数据分别读取,再分别赋值给相关常量。整机停机状态计算是一个多杆的力平衡计算,变量包括主尾起缓冲器的压缩量、主尾起轮胎的压缩量以及停机角。其中主尾起缓冲器载荷计算根据缓冲器的数据计算。为程序的模块化和可读性,编制内部子函数,如整机停机状态的主起缓冲器载荷计算子程序zxmacurve,所需参数通过主程序 zxparking.m里的moleop传递,内部子函数定义如代码4。
function f=zxmacurve(moleop); (代码4)
减缩质量的计算所需的数据包括整机重量重心以及停机状态,因此必须完成停机状态的计算才可进行减缩质量的计算。减缩质量计算时从工作表“所有参数”里读取整机重量重心,从工作表“停机状态”里读取重心高度、主尾起中心到重心的距离等所需数据。
起落架的着陆性能计算是起落架计算的核心内容,一般需要进行不同着陆状态的计算,数据的输入输出量均比较多。计算的状态在工作表“性能计算”里先定义好,所需的交点数据、缓冲器数据、轮胎数据分别从工作表“所有参数”的各数据区域里读取,方法如前所述。单个着陆状态的性能结果存储在单个工作表里如“主起2.44”,见图2。程序的编制方法与其他简单程序一样。为了起落架性能计算的精确,采取的步长较小,输出的数据可能会超过Excel的行数限制,因此在详细数据输出时可以按每隔100个取1个数据进行。这些计算数据的详细输出一方面是为了便于检查校对程序,另一方面是为了便于在起落架结构设计中进行查阅。
这些程序各自独立,可单独运行。调试完成后,再编制总程序zxall.m,将上述程序当做子程序在zxall.m里运行。为完成一种直升机起落架常规计算,作者编制程序9个,总的M代码2000余行。在惠普Z800计算机平台上完成该型机起落架的一次计算(包括主起落架缓冲器的静压曲线计算、尾起落架缓冲器的静压曲线计算、主起落架的静压曲线计算、尾起落架的静压曲线计算、停机状态的计算、减缩质量计算、4个着陆状态的主起性能计算、4个着陆状态的尾起性能计算)耗时约400余秒。程序框图如图4所示。
在Matlab里运行总程序zxall.m,总程序控制各子程序的运行,各子程序从数据文件zxxcalculation.xls的工作表“所有参数”里读入数据,完成计算后将计算结果存储在相应工作表中。这样文件zxxcalculation.xls里存储着整个起落架的常规计算所需的参数和计算结果,计算结果数据和图表条理清晰,可直接进行校对查阅,也可再编辑。如果需要调整某个设计参数,修改zxxcalculation.xls里的该参数,再运行一次总程序zxall.m,即可得到所有计算结果,对照前后zxxcalculation.xls文件,可比较出该参数对着陆性能或停机状态的影响。

图4 集成计算程序运行框图
4 结论
本文详细叙述了采用Excel和Matlab对直升机起落架常规计算进行集成的方法,对输入输出的处理方式及程序的编制进行了详细阐述。为完成一种直升机起落架的常规计算,作者编制了9个计算程序,共2000余行的M代码,在惠普Z800计算机平台上运行该程序,耗时400余秒。输入输出的数据文件zxxcalculation.xls包含所有起落架计算的信息,可直接查阅、校对、分析,也可再编辑。采用这样的集成计算,一方面保证了输入输出数据的完整性、统一性和直观性,另一方面也方便了计算结果的反复比较和设计参数的不断优化。
[1]航空航天工业部科学技术委员会,编.飞机起落架强度设计指南[M].成都:四川科学技术出版社.1989.
[2]徐金明.MATLAB实用教程[M].北京:清华大学出版社.2005.
[3]Math Works公司.MATLAB help[Z].2005.

