起重机小车偏斜对轮轨接触状态的影响
刘 萍,范 勤
(武汉科技大学机电研究所,湖北武汉,430081)
起重机小车偏斜对轮轨接触状态的影响
刘 萍,范 勤
(武汉科技大学机电研究所,湖北武汉,430081)
利用有限元分析软件Ansys对轮轨系统进行弹塑性静力分析,建立起重机小车在运行中发生偏斜和不发生偏斜两种工况下的有限元模型,研究这两种不同工况下轮轨系统所受应力的分布状态。结果表明,小车运行中发生偏斜时,轮轨承受更大的应力,最大应力区集中分布在小车偏斜方向的半边轨道上,且轮缘与轨道之间发生接触,导致轮轨更易磨损。
起重机;有限元法;非线性;偏斜运行;弹性接触
起重机小车运行过程中,主梁弹性变形或下挠、车轮轨道安装精度不够或大小车同时运动等多种原因均会导致小车偏斜,致使车轮轮缘与钢轨发生“啃轨"现象[1]。小车工作过程中发生啃轨会降低车轮使用寿命,加速轮缘和轨道磨损,增加运行阻力。准确计算小车偏斜时轮轨间的应力分布是研究轮轨疲劳损伤问题的基础。
有限元法能够避免经典接触理论中弹性半空间的假设,精确模拟车轮与钢轨的几何形状及其相互接触关系[2],是目前解决轮轨接触问题的主要途径。本文利用有限元软件Ansys分析起重小车在运行中发生偏斜和不发生偏斜两种工况下的应力分布情况,并分析小车运行中发生偏斜对轮轨接触状态的影响。
1 轮轨接触应力的理论计算
当两个中心线平行的圆柱体表面相接触,或一圆柱体的圆柱表面与平面接触时,若接触体均为刚体,那么它们的接触点形成一根直线,称为线接触;若接触体为弹性体,则接触处是宽度为e的长方形,该接触为面接触,接触宽度e上形成对称的按半椭圆曲线分布的表面应力,根据力的平衡原理,其中点的压应力为
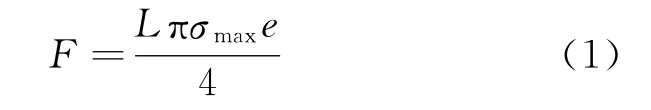
式中:F为接触压力,N;L为有效接触长度,mm;σmax为接触点的压应力,即接触应力,MPa;e为接触宽度,mm。
由式(1)可得:

根据赫兹的弹性接触理论[3],接触宽度e与两接触体折算曲率半径ρ和折算弹性模数E有关,即:
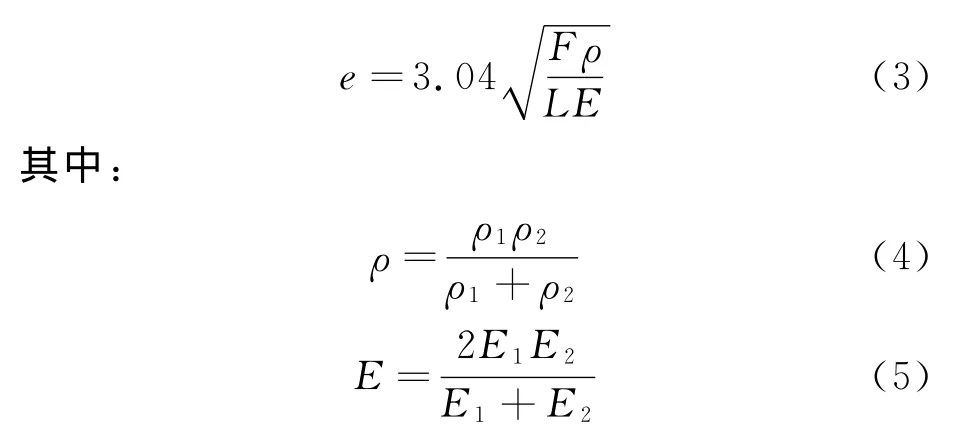
式中:ρ1、ρ2分别为两接触体在接触处的曲率半径,mm;E1、E2分别为两接触体的弹性模量,MPa。
将式(3)代入式(2)中可得:
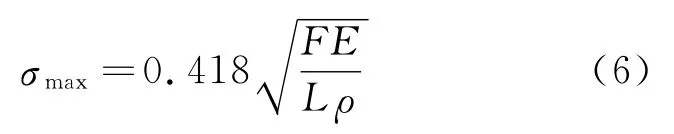
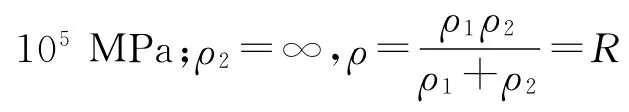
2 接触问题的有限元求解
接触问题属于典型的非线性问题,与一般非线性问题不同的是,它具有独特的接触界面非线性,这来源于两个方面:①接触界面的区域大小、相互位置和接触状态事先未知且随时间变化;②接触条件非线性,包括法向接触条件和切向接触条件,分别用来判定物体是否进入接触和已进入接触的两个物体接触面的具体接触状态。这些约束条件是单边性的不等式约束。有限元求解接触问题的关键就是将这些单边约束条件引入包含等式的变分原理,因此,接触问题通常采用增量方法求解,并且每一步增量均采用试探-校核的迭代方法来判定接触面的范围和接触状态[4]。
3 数学模型的建立
3.1 实体模型
某起重机厂小车运行系统中,小车车轮直径为315 mm,双轮缘为圆柱形踏面;钢轨为45号方钢,断面尺寸为70 mm×70 mm。以该运行系统车轮和轨道的实际尺寸建立三维模型图,如图1所示。根据三维模型图,建立小车无偏斜和偏斜运行时的两种计算模型。两种模型除接触位置和加载不同外,其余设置均相同。
图1 三维模型图Fig.1 Three-dimensional model
3.2 定义单元及材料属性
用Ansys的5种单元类型来模拟轮轨系统,这5种单元类型分别是:①模拟车轮和轨道的三维实体单元Solid95;②模拟车轮轴的梁单元Beam188;③模拟轮轴连接的杆单元link10,设置其属性为只受压;④模拟车轮踏面(柔性接触面)的接触单元Conta174;⑤模拟轨道工作面(目标面)的目标单元Targe170。
系统中材料的特性常数为:弹性模量E为2.1×105MPa,泊松比为0.3,密度为7.85×10-6kg/mm3,重力加速度为9.8 m/s2,取材料的弹塑性本构关系为双线性随动强化(BKIN),屈服极限Re为340 MPa,应变强化模量Ep=0.1E,摩擦系数μ为0.3。
3.3 网格划分
综合考虑计算精度和计算工作量,对远离接触区的实体部分采用较粗的网格划分,而对可能进入接触区的实体部分采用较细的网格[5]。本文采用六面体网格划分,共划分为40 504个单元和44 633个节点。划分网格后轮轨系统的有限元模型如图2所示。
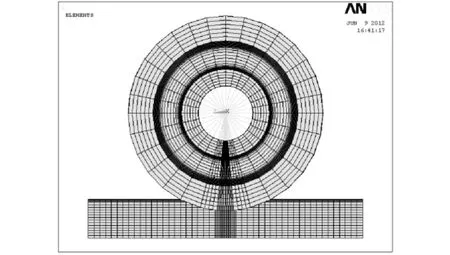
图2 有限元模型图Fig.2 Finite element model
3.4 约束及加载
(1)无偏斜运动时,轮轨系统只受垂直载荷作用,全约束轨道底面所有节点并约束轴端节点沿X方向的旋转,并将车轮最大轮压(177 k N)平均分配到轴两端的节点上。
(2)偏斜运动时,轮轨系统除受垂直载荷作用外还受侧向载荷作用,需全约束轨道底面所有节点并约束轴端节点沿X、Z方向的旋转。侧向载荷的方向垂直于起重机小车运行方向,其值可按下式计算:

式中:P为对轮轨系统最不利的轮压值,k N;λ为侧向力系数。
4 计算结果
小车无偏斜和偏斜运行两种状态下静态车轮系统中轮轨的应力分布等值线图如图3~图6所示。由图3和图4中可见,小车正常运行不发生偏斜运动时,轮轨之间为线接触,接触斑近似为一矩形;轨道最大von-Mises应力为234.3 MPa,应力较大位置主要在接触斑以下0~5 mm处;车轮最大von-Mises应力为244.2 MPa,最大应力位置发生在车轮踏面;轮轨之间的法向接触应力为286.2 MPa。
由图5和图6中可见,小车发生偏斜运动时,轮轨接触状态改变,轮轨系统间发生两处接触:轮轨踏面间为线接触,接触斑仍近似为一矩形;轮缘与轨道侧面为点接触,接触斑为椭圆形。轨道最大von-Mises应力为303.1 MPa,应力分布主要集中在小车偏斜方向的轨道一侧;车轮最大von-Mises应力为400.8 MPa,接触应力为406.5 MPa,且轮缘与轨道之间接触应力约为60 MPa。以上模型模拟结果与赫兹理论的计算结果相吻合。
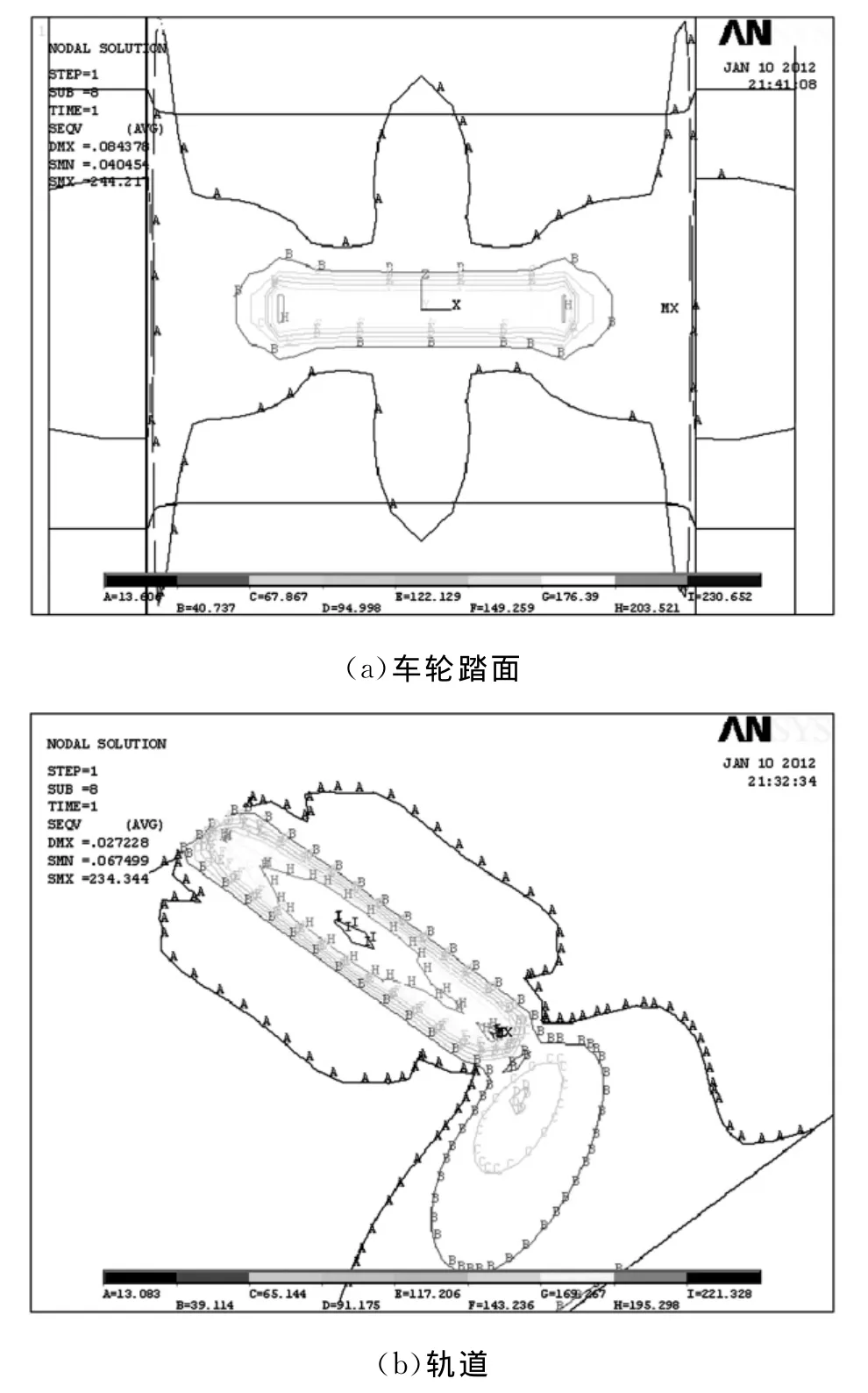
图3 无偏斜时轮轨Von-Mises应力等值线图Fig.3 Von-Mises equivalent stress contour bands without lateral movement
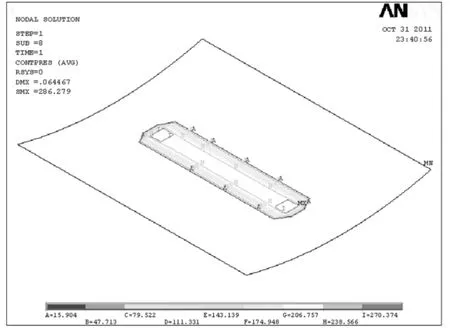
图4 无偏斜时轮轨法向接触应力等值线图Fig.4 Contact stress without lateral movement
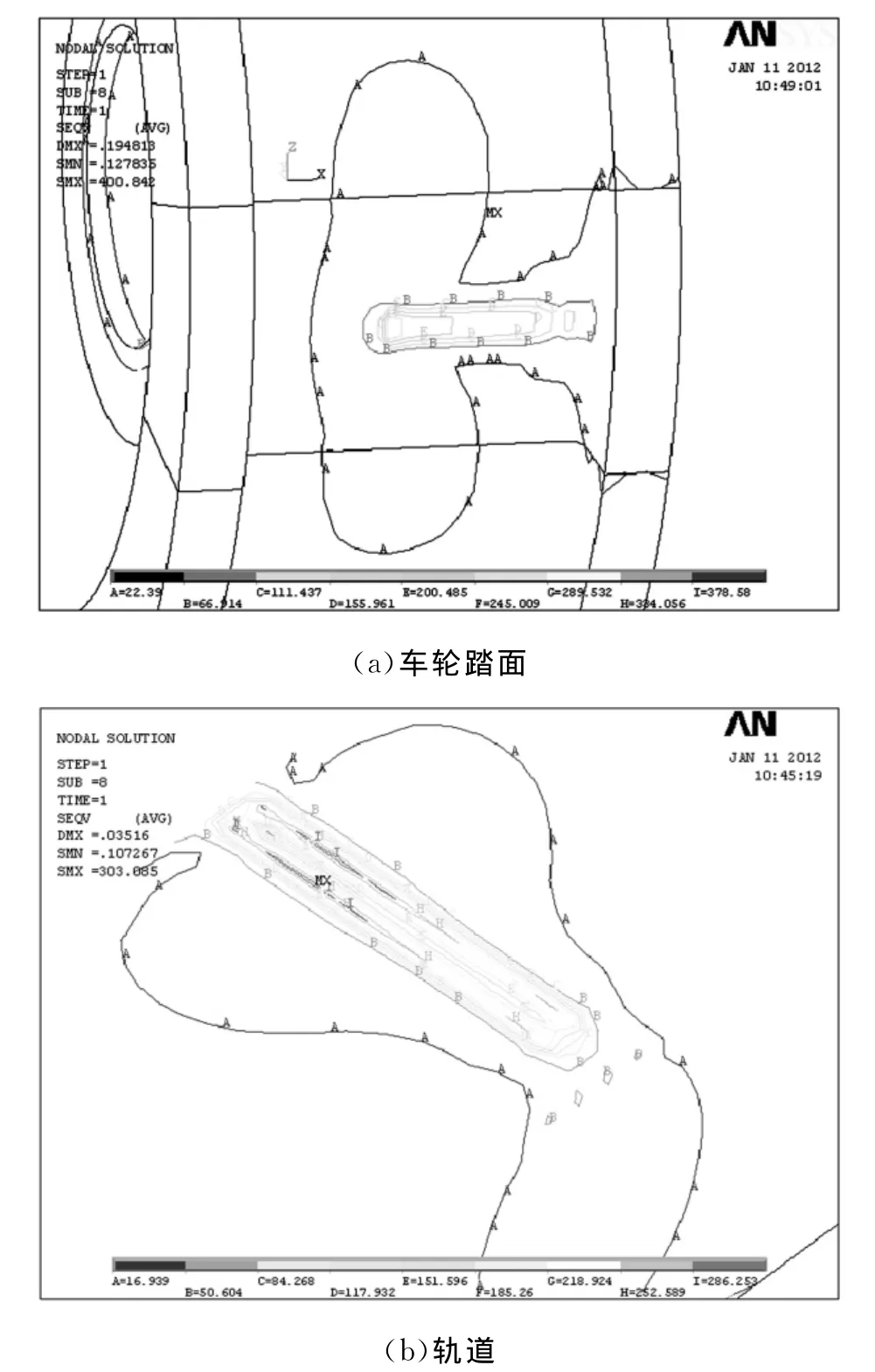
图5 偏斜时轮轨Von-Mises应力等值线图Fig.5 Von-Mises equivalent stress contour bands with lateral movement
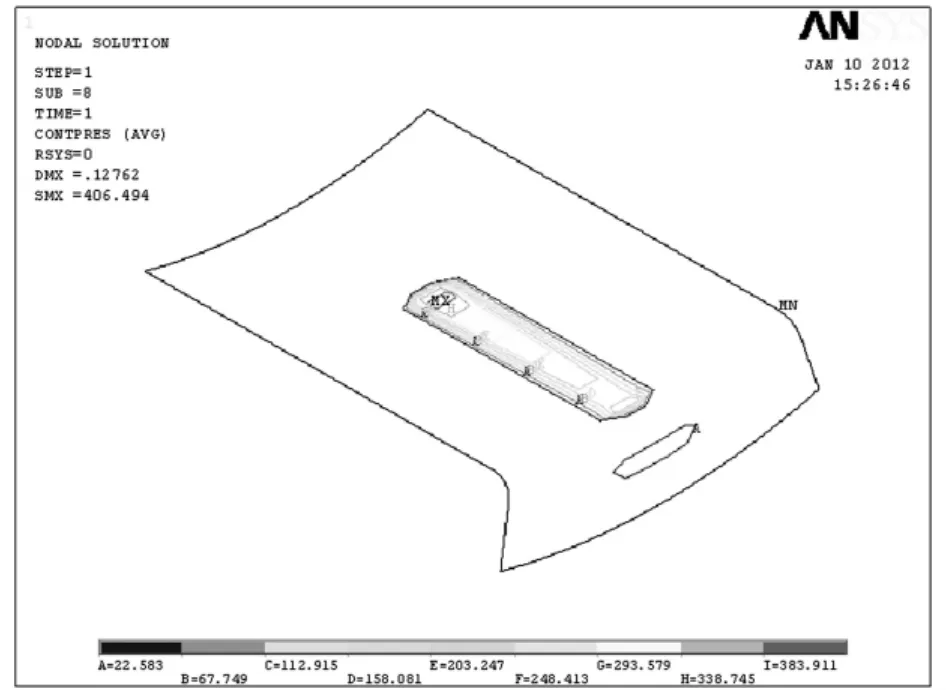
图6 偏斜时轮轨法向接触应力等值线图Fig.6 Contact stress with lateral movement
车轮材料为ZG340-640,抗拉强度σb为640 MPa;轨道材料为45号方钢,σb为650 MPa。线接触时,两材料的许用接触应力σHp可达800~1 000 MPa。由以上两组计算结果可知,小车在正常运行工况下各项应力均满足要求,轮轨材料变形均在弹性范围之内;发生偏斜后,其应力值超出轮轨材料的屈服极限,轮轨材料发生塑性变形,同时接触状态发生改变,接触部位由无偏斜时的一处接触变成两处接触,轮缘与轨道之间发生相互作用,且轮轨所受各项应力值均增大,尤其是垂直接触点的应力显著增大,此时,虽然应力值仍在材料抗拉强度和许用接触应力允许范围内,但是由于轮轨发生塑性变形,故存在点蚀破坏的潜在危险,同时由于轮缘与轨道摩擦加剧,且车轮和轨道的应力都有较大增加,致使两者磨损加剧。
5 结论
(1)起重机小车无偏斜运动时,轮轨只受垂直载荷,车轮与轨道线接触,接触斑近似为一矩形。偏斜运动时,轮轨系统受竖向载荷和横向载荷,车轮与轨道踏面线接触,接触斑近似为一矩形;轮缘与轨道侧面点接触,点接触斑为椭圆形。
(2)小车偏斜运动时,轮轨系统需要承受更大的应力,车轮和轨道发生塑性变形,存在点蚀破坏的潜在危险,最大应力区集中分布在小车偏斜方向的半边轨道上,且轮缘与轨道之间发生相互作用,使轮缘、轨道磨损加剧,车轮寿命降低。
(3)采用有限元方法分析起重机小车轮轨系统的接触状态有效适用。
[1] 史向东.桥式起重机大小车轨道啃轨的检测分析与研究[J].机械设计与制造,2010(5):267-268.
[2] Zhang Jun,Sun Shouguang.Numerical simulation of two-point contact between wheel and rail[J].Acta Mechanica Solida Sinica,2009,22(4):352-359.
[3] Johnson K L.接触力学[M].徐秉业,等译.北京:高等教育出版社,1992.
[4] 王勖成.有限单元法[M].北京:清华大学出版社,2003.
[5] 禹昭.起重机轮轨弹塑性接触有限元分析[J].机械工程及自动化,2008(1):57-61.
Effect of lateral movement of overhead crane carriage on wheel-rail contact state
Liu Ping,Fan Qin
(Institute of Mechatronics,Wuhan University of Science and Technology,Wuhan 430081,China)
ANSYS,an FEM software,was used to solve the elastic-plastic and static wheel-rail contact problem.The real geometry of wheel-rail were simulated and the finite element model of the overhead crane carriage with or without lateral movement was established.The stress distribution under the two different operating conditions of the wheel-rail system was studied.The results show that the wheel-rail system with lateral movement has greater stress,and the contact happens between the rim of wheel and the rail.As a result,the wheel and the rail are more likely to wear.
overhead crane;FEM;nonlinearity;lateral movement;elastic contact
TH215
A
1674-3644(2012)04-0317-04
[责任编辑 郑淑芳]
2011-12-22
刘 萍(1985-),女,武汉科技大学硕士生.E-mail:wust6622@126.com
范 勤(1960-),男,武汉科技大学教授,博士.E-mail:fanq_wust@126.com

