拉伸弯曲矫直机机组动态仿真分析

肖 义，刘安中，肖 涵

（武汉科技大学机械自动化学院，湖北武汉，430081）

拉伸弯曲矫直机机组动态仿真分析

肖 义，刘安中，肖 涵

（武汉科技大学机械自动化学院，湖北武汉，430081）

建立拉伸弯曲矫直机机组及其钢结构平台的有限元分析模型，并利用有限元分析软件对其进行动态仿真分析。结果表明，在载荷工况下将不同频率的谐响应仿真曲线进行叠加，得到机组振动的仿真结果；提取其对应实际测点位置的振动烈度值（Vrms2），将已仿真计算得到的机组在混凝土基础上时测点的振动烈度值（Vrms1）进行比较，得到各测点振动烈度的对应比值Ai；根据比值Ai与实测机组在混凝土基础上的振动烈度值（Vrms0）来预估机组在钢结构平台的振动情况，发现其振动烈度值满足现场要求。

拉伸弯曲矫直机；钢结构平台；动态分析；振动烈度

某钢厂酸轧生产线需提速改造，将原有位于混凝土基础上的拉伸弯曲矫直机（简称拉矫机）机组移至钢结构平台上。由于原混凝土基础上的机组振动情况良好，钢结构平台较之混凝土基础为柔性基础，故机组移至钢结构平台后其振动加剧。为掌握改造后钢结构平台机组的振动情况，需要对其进行动态分析。为此，本文以拉矫机机组及钢结构平台为对象，利用有限元（FEA）分析软件对其进行动态仿真分析，并在载荷工况下将不同频率的谐响应仿真曲线进行叠加，得到机组振动的仿真结果。

1 FEA模型描述

在建立钢结构平台和拉矫机机组有限元模型时，考虑到两者结构都比较大且复杂（见图1），可将其分为钢结构平台和拉矫机机组两部分单独建模，然后再将两部分的模型通过中间层连接起来。

1.1 拉矫机机组的建模

拉矫机机组建模采用三维实体模型划分网格的方法来生成FEA模型。拉矫机机组的前后张力辊主传动系统的结构简图如图2所示。由图2可看出，拉矫机机组的振动主要来自各传动齿轮箱的振动，在分析建模时，只取4个齿轮箱为分析对象，忽略电机、齿轮箱之间的联轴器、油管等元件［1］。建模步骤如下：①依照设计图纸建立其三维实体模型，适当简化对整体结构影响不大的细小结构（轴等零件的键槽、倒角等）和零件（垫圈、端盖、螺栓、油塞等）［2］；②将三维实体模型导入有限元分析软件中，采用三维实体单元来划分网格，针对不同大小的实体可依次分级划分网格；③模型建立完成后，根据载荷工况对其进行动态仿真分析，并通过主要测点振动烈度的仿真值与实测值的对比来校验模型，反复修改模型，保证其准确性。

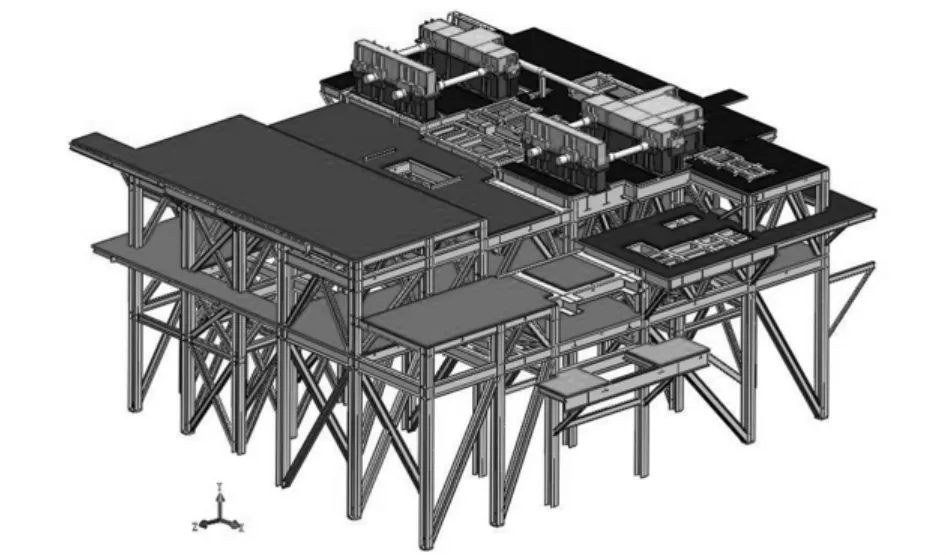
图1 拉矫机机组和钢结构平台的三维实体模型Fig.1 Three dimensional solid model of the whole unit of tension leveler and its steel structure platform

1.2 钢结构平台的建模

钢结构平台建模采用在有限元分析软件中直接进行建模。由设计图纸可知，其由不同类型的型钢（H型、L型、C型等）和钢板组接而成（见图1）。建模步骤如下：①以线体代表型钢，以面代表钢板建立钢结构平台的框架模型（忽略楼梯，护栏等辅助元件）；②选用梁单元（可设置不同的截面特性），设置不同型钢的截面特性赋予线体，再对其进行网格划分［3－4］；③选用壳单元（计算量小，且在承受弯矩的情况下，计算误差小）对所建立的面划分网格。

1.3 整体模型的建立

在建立完成拉矫机机组的FEA模型后，将其对应的三维实体模型导入已建立好的钢结构平台的FEA模型界面中。按照设计图纸设置导入实体模型的参照坐标系，保证导入后拉矫机机组与钢结构平台之间处于正确的安装位置。由设计图纸可知，机组与平台之间通过安装底座定位，然后采用二次灌浆层固接而成。在建立中间层的FEA模型时，主要以灌浆层为分析对象，省去安装底座和联接螺栓。由于中间层的厚度尺寸与长度尺寸相差较大，故可以选择板单元对其进行网格划分。中间层通过在机组箱体底面的面和钢结构平台上的线体来建模。

建立FEA模型时设置的主要物理参量如表1所示。所建立的拉矫机机组和钢结构平台整体的FEA模型如图3所示。

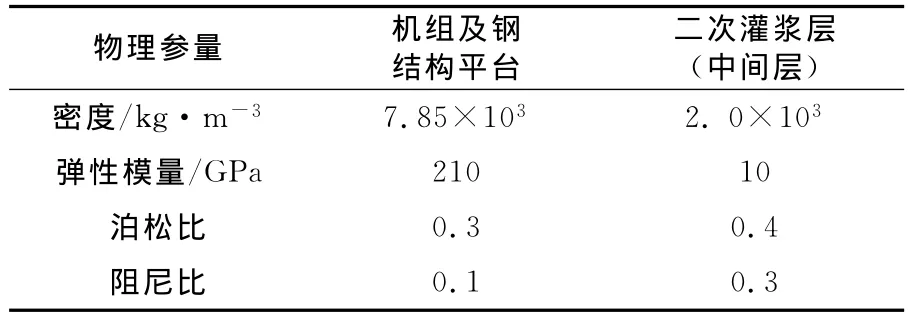
表1 FEA模型中的主要物理参量Table 1 Main physical parameters in the FEA model

图3 拉矫机机组和钢结构平台整体的FEA模型（加边界条件）Fig.3 FEA model of the whole unit of tension leveler and its steel structure platform

2 模态分析

模态分析是所有动态分析的基础。首先，通过模态分析得到模型的固有频率和主振型。固定钢架各立柱下端点的6个自由度（见图3），设定模态提取阶数为5，扩展模态的阶数也为5。设置扩展模态是为方便在结果中查看各阶振型图［2，5］。计算得到拉矫机机组和钢结构平台整体的固有特性如表2和图4～图6所示。

表2 拉矫机机组与钢平台整体的固有特性Table 2 Inherent characteristics of the whole unit of tension leveler and its steel structure platform

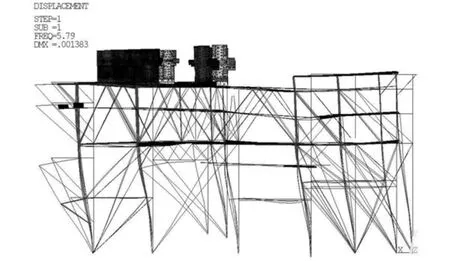
图4 第1阶主振型Fig.4 First main vibration mode

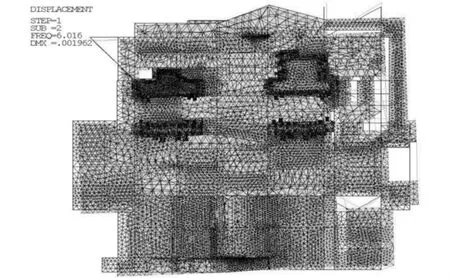
图5 第2阶主振型Fig.5 Second main vibration mode

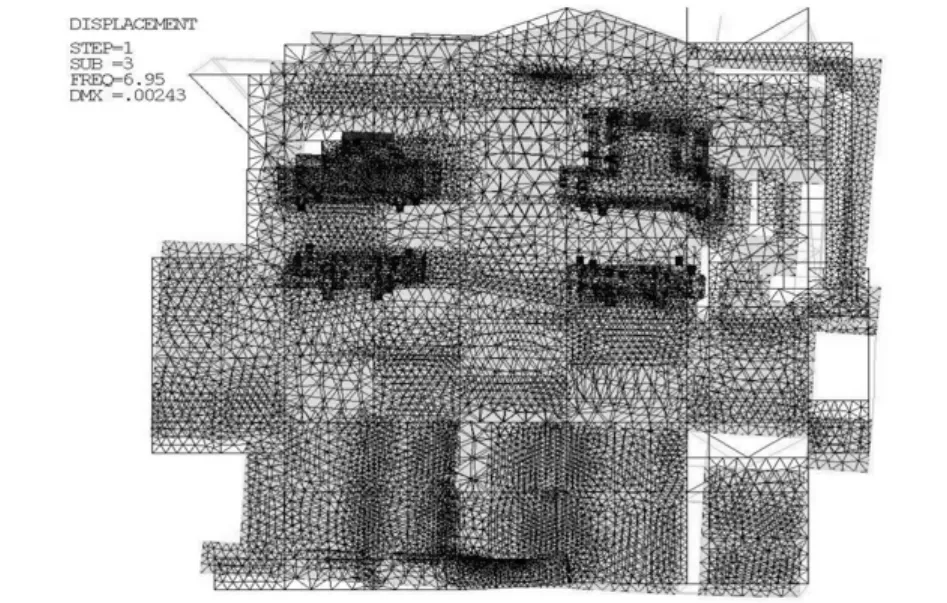
图6 第3阶主振型Fig.6 Third main vibration mode

3 谐响应分析

谐响应分析是用于确定结构在承受随时间按正弦规律变化载荷时的稳态响应［5］。拉矫机机组的振动主要是由齿轮啮合产生的，因此可将机组所受载荷转化为齿轮的啮合力，并以简谐载荷的形式表示。

根据谐响应分析获得的位移响应x可计算得到相应的振动烈度（速度均方根值）v＝0.7× 2πf x，式中：f为啮合频率，Hz。由于存在多种幅值及频率的激励，且作用点各不相同，因此采用将各谐响应仿真曲线进行叠加来计算测点的振动烈度。图7为叠加法计算测点振动烈度模型的示意图。

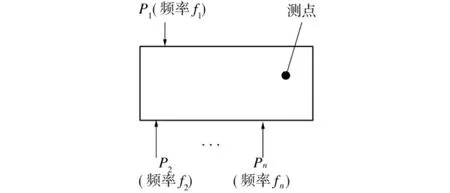
图7 叠加法计算测点振动烈度模型的示意图Fig.7 Diagram of the model for calculating the vibration intensity of position by superposition method

设含n个不同频率的激励振动系统，该系统受到的激励分别为

式中：Pi为激励幅值，N；fi为Pi的激励频率，Hz。

对激励振动系统进行分析时，分别施加激励Pi。设各激励Pi在测点处的位移响应分别为

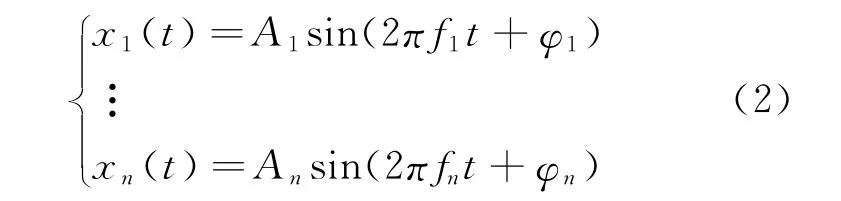
式中：A1，…，An分别为n个激励在测点处产生的位移响应峰值；φ1，…φn分别为各位移响应的相位差。

则测点处的位移响应为

测点处的速度响应为

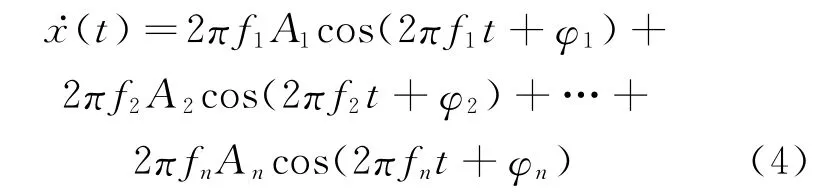
测点处的振动烈度（速度的均方根值）为

3.1 激励分析

根据现场机组的运行参数和拉矫机的相关设计资料［6］可计算得到拉矫机各齿轮箱所受的载荷。动态分析时所施加的激励数据如表3所示（各齿轮副位置见图2）。

3.2 混凝土基础机组的响应

将同频率的激励一次加载进行谐响应分析，分别施加在对应齿轮副的啮合处。设置谐响应分析的频率范围，阻尼比为0.1。

将表3中由各激励计算得出的谐响应结果叠加得到各测点（见图2）的振动烈度值。这些测点都是现场在线监测系统中的实际测点。混凝土基础上振动烈度的仿真计算值Vrms1与实测值Vrms0对比列于表4中。由表4可看出，振动烈度仿真值与实测值的相对误差表明所建立的拉矫机机组的FEA模型的准确性，此模型可以作为后续分析的基础。

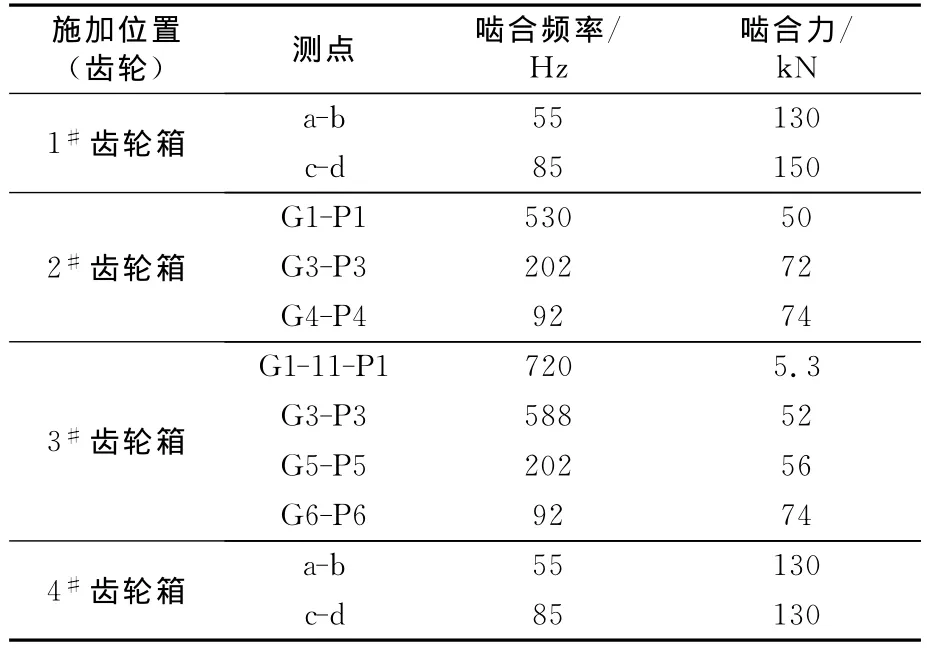
表3 各箱体谐响应分析所加激励数据Table 3 Incentive data exerted on each box in the harmonic response analysis

表4 仿真与实测振动烈度对比Table 4 Contrast of simulation and measured vibration intensities

3.3 钢结构平台机组的响应

激励数据和相关设置与混凝土基础上机组保持一致，按照相同的方法加载不同频率的激励，计算得出钢结构平台机组测点的振动烈度值Vrms2。将振动烈度的实测值、混凝土基础上的仿真值及钢结构平台的仿真值对比一并列于表5中。

由表5中钢结构平台的仿真值可看出，机组移至钢结构平台上后，其振动情况会加剧，测点的振动烈度的数值明显高于混凝土基础上的仿真值。

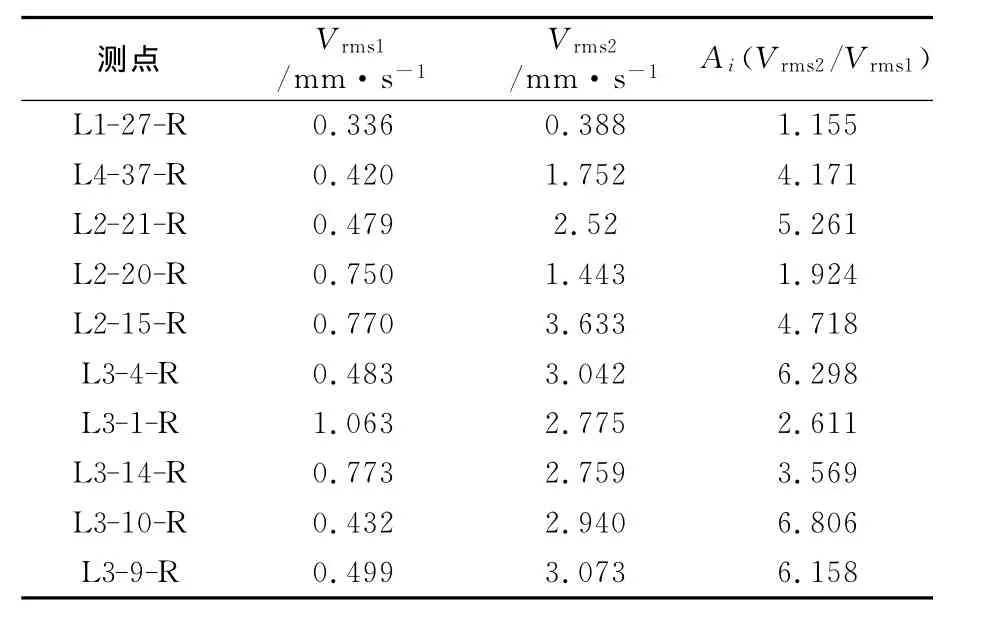
表5 振动烈度值仿真计算结果对比Table 5 Contrast of simulation results of vibration intensity

4 结论

（1）由仿真结果可知，拉矫机机组由原混凝土基础移至钢结构平台后，各测点的振动烈度均有所增加。根据国际标准ISO2372和ISO3945的规定，钢结构平台机组振动等级为良好。

（2）在建立分析对象的FEA模型时，针对其特点运用不同的方法对钢结构平台和拉矫机机组两部分实行单独建模，而后再组合成整体的模型。在保证各部分模型准确建立的前提下，组合时保持各部分模型之间的空间位置关系及设置的物理参数不变，由此保证了组合后整体模型的准确性。

（3）对于钢结构平台使用线体直接建模，而对拉矫机机组使用实体建模，与统一运用实体建模相比，提高了建模效率和模型分析计算的可行性，使建立的分析模型经济实用，且降低了对硬件的要求。

［1］ 刘晓东，吴入军.车床主轴箱模态分析［J］.机械设计与制造，2007（2）：24－25.

［2］ 李顺德，孙华刚，冯广斌，等.试验用齿轮箱轴系耦合振动有限元模态分析［J］.机械制造，2010，48（546）：72－74.

［3］ 龚曙光.ANSYS工程应用实例解析［M］.北京：机械工业出版社，2003：15－32.

［4］ 《轻型钢结构设计手册》编辑委员会.轻型钢结构设计手册 ［M］.北京：中国建筑工业出版社，2006：264－332.

［5］ 任重.ANSYS实用分析教程［M］.北京：北京大学出版社，2003：43－50，177－247.

［6］ 周国盈.带钢精整设备［M］.北京：机械工业出版社，1979：1－9.

Dynamic simulation analysis of tension leveler unit

Xiao Yi，Liu Anzhong，Xiao Han
（College of Machinery and Automation，Wuhan University of Science and Technology，Wuhan 430081，China）

The finite element analysis model of the whole unit of tension leveler unit including its steel structure platform was established.In order to obtain the vibration simulation results of the unit，the simulation harmonic response at different frequencies was superposed based on the simulation of loads in operating condition，and then the vibration intensity value（Vrms2）of positions corresponding to the actual landmarks was extracted from the simulation results，which was compared with the simulation vibration intensity value（Vrms1）of the landmarks when the unit was placed on the concrete base.The ratios Ai of vibration intensity for each landmark were obtained.Finally，the Ai and the actual measured vibration intensity value（Vrms0）of the landmarks of tension leveler unit placed on the concrete base were used to predict the unit＇s vibration when it was moved on to the steel structure platform，and the results show that the vibration intensity value satisfies the requirements.

tension leveler；steel structure platform；dynamic analysis；vibration intensity

TG333.4

A

1674－3644（2012）04－0312－05

［责任编辑 徐前进］

2012－02－12

湖北省高校产学研合作重大资助项目（CXY2009A002）.

肖 义（1986－），男，武汉科技大学硕士生.E－mail：409660975＠qq.com

肖 涵（1979－），男，武汉科技大学副教授，博士.E－mail：coolxiaohan＠163.com