状态价格向量的对偶性研究

○王素琴

（湖北第二师范学院数学与数量经济学院湖北 武汉 430205）

套利是投资者最为关注的内容，也是投资者寻找的内容，它充实着金融市场。套利是研究金融中均衡性和公平性的重要工具，所以，无论是理论还是实证，套利一直都是金融领域研究的主要课题。

研究套利的理论有很多，其中很多都是数理金融理论中最重要的理论基础，这些既被用于研究套利，也被用于导出数理金融中的其他结论。研究套利的方法很多，如中性概率分布和状态价格向量，也有很多方法来证明相关理论结论，这些方法各有优劣，可以从某些方面揭示套利的实质。

单纯从数学上看，套利实际为两组线性不等式组的关系。本文利用线性不等式组、线性系统或线性锥系统的择一性和对偶性来构造状态价格向量，并说明无套利与状态价格向量为一对偶关系，进而说明中性概率分布和状态价格向量之间的关系。

一、预备知识

1、一些记号

设市场有n个风险资产，每种资产在未来时刻1有l个状态，第i个资产在第j个状态出现时的收益率为ri（j），价格为Pji（i=1，2，…，n；j=1，2，…，l）。记：

投资策略向量（资产组合）：x=（x1，x2，…，xn）T；

概率向量：p=（p1，p2，…，pl）T；

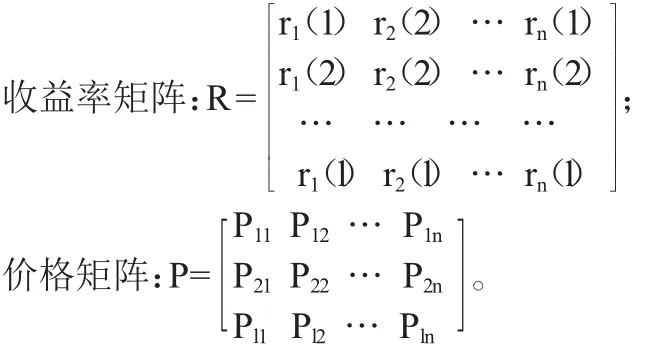
第i个资产在当前时刻0的价格（初始价格）为vi（i=1，2，…，n），记：

初始价格向量：v=（v1，v2，…，vn）T；

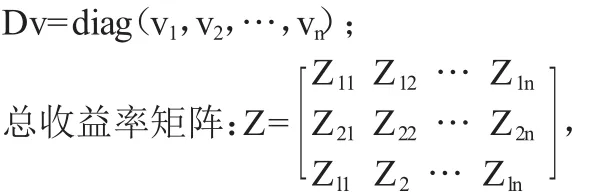
其中：Zji=Pji/vi（i=1，2，…，n；j=1，2，…，l）为在时刻1状态j出现时第i个资产的总收益率，有关系：

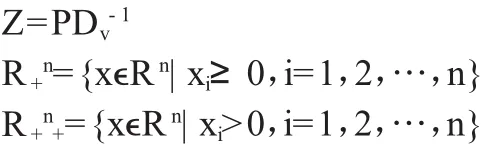
如果 x∈R+n，x≠0，则称 x≥0，同样可以定义 x≥y。

2、择一定理

设A是矩阵，x、u是列向量。

引理1 对齐次线性不等式组：

（Ⅰ） Ax≥0；

（Ⅱ） ATu=0、u＞0，

则（Ⅰ）有解的充分必要条件是（Ⅱ）无解。

引理 2 设 x∈Rn、u∈Rm、A∈Rm×n；Cx为 Rn中其锥，其对偶锥为C*x，考虑线性锥系统：

（Ⅰ） x∈Cx，Ax≥0；

（Ⅱ） -ATu∈C*x，u＞0，

则（Ⅰ）有解的充分必要条件是（Ⅱ）无解。

3、套利定理

引理3（套利定理）下列结论有且只有一个正确：

（Ⅰ） 存在投资策略x使得：Rx＞0；

（Ⅱ） 存在概率向量p使得：RTp=0。

套利定理表明，在所有的状态集合中，要么一定有套利，要么一定无套利。并且在无套利情况下，存在一个概率分布，在这个分布下，每种投资的期望收益均为0，这个概率分布也称为风险中性概率分布。

二、状态价格向量的构造

1、概念

套利机会：如果有投资组合x满足下列条件之一：

（1） vTx≤0，Px≥0

（2） vTx≥0，Px≤0

则称存在套利机会，反之亦然。

即在0和1时刻资产组合价值的正负性不同，则有套利机会。

状态价格向量：如果有α∈Rl满足：

PTα=v 或 ZTα=1

则称向量α为支持资产系统P或Z的状态价格向量。

当资产系统存在价格向量时，每种资产在0时刻的价格向量都可以用1时刻资产在各种状态的价格线性表示。

2、状态价格向量的构造

定理1资产系统不存在套利机会的充分条件是存在支持该资产系统的状态价格向量α∈R+l+。

证明：由套利机会的定义，不存在套利机会等价，下列两组线性不等式组无解：

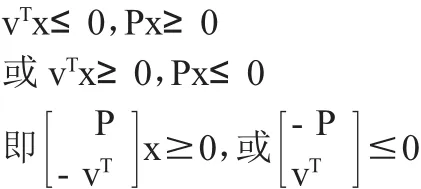
无解。

由引理1，此二线性不等式组等价：

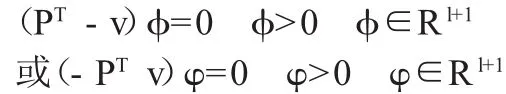
有解。

统一为：

有解。

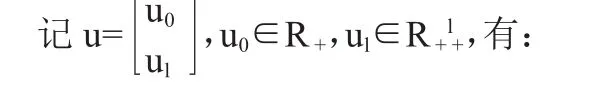
证毕。

三、结论与讨论

判断套利的方法有很多种，判断状态价格向量是否存在就是其中的方法之一。

从单纯数学角度上看，判断套利只是关于一类线性不等式组的一个关系问题，而择一定理正是处理和揭示这类线性不等式组一些性质的理论基础，所以，从简单思维上看是很容易将两者结合起来的。

以下是用择一定理来证明无套利与存在状态价格向量等价，从证明过程可见，证明过程简洁明了，也很简单。

1、利用线性锥系统的择一定理（引理2）来证明这个结论

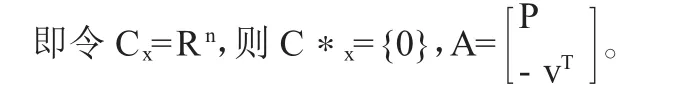
由引理2即可得到（1）式。

可见，无套利与状态价格向量实为一对偶关系，这为套利的应用提供了理论基础和广阔的领域。

2、套利定理（引理3）和定理1都是判断套利的等价条件

套利定理表明，无套利的等价条件是存在风险中性概率，使每种投资期望收益均为0的。

定理1表明无套利的等价条件是存在正状态价格向量，使每种资产在0时刻的价格向量都可以用1时刻资产在各种状态的价格正线性表示。

由此可得，存在风险中性概率和存在正状态价格向量也是等价的。

当然，可以进一步讨论风险中性概率和状态价格向量之间的关系。

[1]宋军、吴冲锋、马弋崴、孙秀琳：保证金制度、跨市套利和沪铜主力合约的迁徙行为[J].系统工程理论与实践，2008（8）.

[2]毛二万、宋逢明：风险套利和资产定价第一基本定理[J].系统工程理论与实践，2001（11）.

[3]潘青飞、安中华：判断市场套利的一种方法[J].武汉理工大学学报，2008（7）.

[4]易艳春、吴雄韬：有限离散时间金融市场模型的无套利定理[J].衡阳师范学院学报，2010（3）.

[5]郭多祚：数理金融资产定价的原理与模型[M].清华大学出版社，2006.

[6]Sheldon M.Ross：数理金融初步[M].机械工业出版社，2005.

[7]魏权龄、闫洪：广义最优化理论和模型[M].科技出版社，2003.

[8]安中华、安琼：线性锥系统的Gordan型择一定理[J].湖北大学学报（自然科学版），2008（4）.