基于2D-FrFT多阶次特征融合的人脸表情识别方法

穆晓敏，张嗣思，齐 林

(郑州大学信息工程学院，河南郑州450001)

0 引言

近几年，对于人脸表情识别已经有了广泛的研究.视觉图像特征被公认为是反映人类表情状态最重要的信息之一.表情识别的关键技术包括特征提取和分类器设计.Wang等人［1］利用Gabor小波提取视觉图像特征，并采用基于FLDA的分类器进行表情识别，平均识别率为49.29%.但是这种方法的计算复杂度较高，且识别率不高.分数阶傅里叶变换(FrFT)是近年发展起来的一种新型时频分析工具，类似于传统的二维傅里叶变换，2D-FrFT的相位函数包含了图像的纹理信息，变换阶次不同，相位函数所含的图像边缘信息也不同，这使得分数阶傅里叶变换可以更加灵活的用于图像的边缘提取和识别［2］.文献［2］首次将2D-FrFT应用于人类表情识别，其思想是将2D-Fr-FT若干阶次下提取到的图像相位信息进行分类识别，平均识别率达到54.17%.

分析文献［2］的实验结果，可以发现在二维分数阶傅里叶域内，不同表情的特征奇异性与变换阶次密切相关，因此不同表情的最高识别率将对应于特定的阶次;同一阶次下不同表情的识别率也与该阶次下表情特征的奇异性密切相关，因此同一阶次下不同表情的识别率也不同.基于上述分析，在不同阶次之间进行特征融合以取得更好的识别率成为可能.笔者在文献［2］的基础上，提出一种在分数阶傅里叶域内两个不同阶次之间进行特征融合的表情识别方法.该方法的思想是寻找两个对所有表情均有较高识别率的变换阶次，利用其分数阶域特征构成两组维数相同的特征矢量，然后利用典型相关分析法(Canonical Correlation Analysis，CCA)进行两个阶次的特征融合，融合后的特征采用基于支持向量机(Support Vector Machine，SVM)的多层分类机制进行识别.利用加拿大瑞尔森大学提供的人脸数据库对所提方法进行了仿真实验，仿真结果表明该方法不仅使得表情识别率较单阶次下有明显的提高，而且所采用的融合算法降低了表情特征的维数，减小了计算量.

1 基于特征融合的人脸表情识别算法描述

1.1 基于特征融合的人脸表情识别框架

笔者提出的基于特征融合的人脸表情识别方法原理如图1所示.通常原始图像样本直接利用2D-FrFT提取表情特征时，变换维数很高，导致运算量很大.为了减小运算量，首先要对原始图像样本进行降维预处理，其目的是提取对识别具有重要意义的奇异信息，去除冗余信息.常用的降维方法有:最邻近线性差值法、主成分分析法、独立成分分析法等［1］.

特征融合的基础是选定针对生气、沮丧、害怕、高兴、悲伤、惊奇等6种基本表情都有较高识别率的两个变换阶次，这是算法的前提.在此基础上设计特征融合算法和分类决策机制.该方法主要包含4个步骤:(1)为减小运算量，先对原始图像进行降维预处理;(2)根据实验结果选择2DFrFT中识别率较好的两个阶次提取到的表情特征构成两组特征向量;(3)设计融合算法进行两个阶次下分数阶傅里叶域特征融合;(4)利用基于SVM的多层次分类机制进行分类与识别.

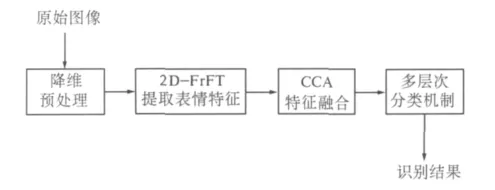
图1 基于2D-FrFT特征融合的表情识别框架Fig.1 The framework of emotion recognition based on 2D-FrFT

1.2 基于CCA的特征融合算法

由H.Hotelling［4-5］提出的典型相关分析法(CCA)是处理两组随机矢量之间相关性的统计方法.利用该算法的统计结果可以把两组随机变量之间的相关性研究转化为少数几对不相关变量之间相关性的研究.将该算法用于多阶次特征融合不仅可以降低表情特征的维数，而且所抽取的典型相关特征具有良好的分类性能.

将CCA算法用于两个阶次特征融合的关键是确定投影方向及寻找两组随机变量在投影方向上的典型相关矢量.假设在图2中，用于特征融合的2D-FrFT两个阶次分别为a和b，将阶次为a和b时提取到的图像相位信息看成是两组多维随机变量，并分别用x和y表示.按照CCA的基本思想找到一组典型投影矢量u和v，通过投影得到x在u上的投影矢量X*，y在v上的投影矢量Y*，写成如下形式:

式中:pi和qi即为一对典型相关特征矢量(i=1，2，…，n，n=min［x的维数，y的维数］)，且每对典型相关特征矢量之间保持最大相关性，各对之间不相关.

每对典型相关特征矢量均对应一个相关系数r(0≤r≤1)，r代表了每对典型相关特征矢量的相关程度，r越趋近于1说明相关程度越高.通常会参考r值的大小选择m(m≤n)对典型相关特征矢量组成融合特征，这样只需分析m对典型相关特征矢量的关系即可达到对x和y之间的相关性分析［6］.

投影后的融合特征可以写成:

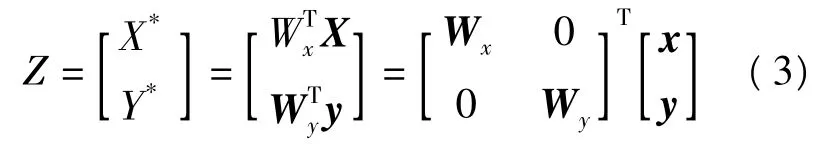
式中:Wx和Wy为典型投影子矩阵，又称融合矩阵.Z为最终用于分类识别的融合特征，Z融合了2D-FrFT域中两个最优阶次下提取到表情特征，并通过CCA消除了信息冗余，融合后降低了表情特征的维数.

1.3 多层次分类机制

采用多层次分类机制［7］是为了减少参与每层分类的类别数，从而将每层分类过程控制在一个类别数较少的范围内，这样更容易控制分类过程.同时也减少了误判，有益于识别率的提高.

多层次分类机制的最终目标就是为了取得可靠的分类结果和更加准确的识别率.鉴于SVM在模式识别和分类方面所表现出的可靠性［8］，将多个基于SVM的基本分类器的输出进行组合形成一个多层次分类器.多层次分类机制的结构如图2所示:

图2 多层次分类机制Fig.2 The multiclassifier scheme

假设 6 种基本表情状态(AN，DI，FE，HA，SA，SU)为6种不同类别，标号1至6.分类器设计为两层，设置分类决策机制如下.

第一层分类机制:由于SVM适合解决二元分类问题且两类分类器的训练代价小，因此首先将6种基本表情类别中任意两类进行组合(C26=15)，通过训练样本建立对应的15个基本分类器.分析待识别样本通过第一层分类器后得到的15个分类结果，该样本被归类为15个分类结果中类别号出现频度最高的类别.如果存在两个或多个类别号出现的频度相同而无法判决时，意味着此待识别样本的表情特征模糊于两种或多种表情，此种情况下需通过第二层分类器区分出不同表情特征之间的细微差异，做进一步识别.

第二层分类机制:考虑第一层分类结果可能出现以下4种情况:两个类别、三个类别，四个类别、五个类别出现频度相同造成无法判决，因此在第二层构建了针对不同情况的多个组合特征分类器，每个分类器参与组合的类别视要甄别哪些表情类别而定.

2 仿真实验及结果分析

仿真采用加拿大瑞尔森大学电子与计算工程学院提供的人脸数据库，该数据库采集了来自6个不同国家、不同文化背景的人在自然状态下的高兴、沮丧、生气、害怕、惊奇、厌恶等人脸6种基本表情样本，样本均为112×96的8位灰度图像.从中选取300幅样本进行仿真，为减小运算量，先利用最邻近线性差值法对图像进行降维处理，得到降维后的 48 维图像［1，2，3］.

2.1 平均识别率与变换阶次之间的关系

将降维后图像进行二维分数阶傅里叶变换，提取到图像的 48 维表情特征［1，2，3］，送入多层次分类器进行分类识别.根据分数阶傅里叶变换的对称性质，笔者变换阶次取值从0.1到2.0［3］，其对应的平均识别率如下图3所示:

图3 2D-FrFT各阶次下表情的平均识别率Fig.3 The average recognition rate under different orders of 2D-FrFT

由图3可以看出，当变换阶次为0.5和1.4时均取得了58.3%的平均识别率，明显优于其他阶次，表明这两个阶次下提取到的表情特征针对不同表情的可区分性较强.因此选择在阶次为0.5和1.4之间进行基于CCA的特征融合.

2.2 融合特征维数对表情识别率的影响

根据CCA原理，x、y分别在u、v上投影得到的m对典型相关特征矢量构成了最终用于识别的融合特征Z，Z的维数(2×m)对表情识别率有着直接影响.笔者通过仿真验证了融合特征Z维数对识别率的影响，结果如图4所示.由图4可以看出融合特征维数对表情识别率有一定影响，存在着融合特征的最佳维数.当m取18对典型相关特征矢量即Z为36维时，达到最高识别率75%.

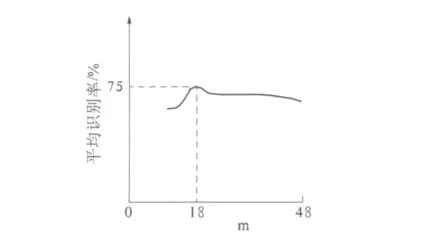
图4 平均识别率随典型相关特征矢量对数m的变化情况Fig.4 The change of average recognition rate in situation to the number of canonical correlation feature pair

2.3 识别率比较

为了验证多阶次特征融合的识别效果，将融合特征Z为36维时6种表情的识别率与单阶次0.5和1.4时的识别率进行了比较，结果如图5所示.

图5 特征融合前后的各表情识别率对比Fig.5 The comparision of recognition rate between before and after feature fusion

从图5可以看出，在未做特征融合时，当变换阶次为0.5和1.4时，平均识别率最高均为58.3%，同一阶次下不同表情的识别率并不相同.这就意味着表情特征值的奇异强烈地依赖于变换阶次，因此识别率的高低也与变换阶次的选择紧密相关.利用CCA对阶次0.5和1.4提取到的表情特征进行融合后，平均识别率达到了75%，较单阶次下平均识别率有明显提高.2D-FrFT中阶次分别取0.5和1.4时提取到的表情特征对不同表情的针对性各有偏重，特征融合将不同阶次下的有效信息进行融合并消除冗余信息，实现了信息之间的互补.

3 结论

在文献［2］的基础上，提出了基于2D-FrFT多阶次特征融合的人脸表情识别方法.仿真实验结果表明经过特征融合后达到的平均识别率75%较未融合时单阶次下的平均识别率58.3%有了大幅提高，这表明通过特征融合对不同阶次下提取到的表情特征起到了互补作用，融合后特征针对同种表情实现了共性最大化，针对不同表情实现了差异性最大化，从而提高了识别率.同时由于采用CCA融合算法也降低了表情特征维数，减小了计算量.另外，对表情识别框架进行分析可知，预处理算法的选择也直接影响识别率，仿真中采用了基于最邻近线性差值法的降维方法［1］，该方法计算复杂度小适合实时处理，但可能丢失部分信息.未来将尝试采用主成分分析法(PCA)、独立成分分析法(ICA)等其他降维预处理方法.同时，多阶次下的特征融合也将是下一步研究的重点.

［1］WANG Yong-jin，GUAN Ling.Recognizing human emotional state from audiovisual signals［J］.IEEE Trans.Multimedia，2008，10(5):936-946.

［2］QI Lin，CHEN En-qing，MU Xiao-min，et al.Recognizing human emotional state based on the 2D-FrFT and FLDA［J］.2nd Image and Signal Processing Conference，2009:1-4.

［3］GAO Lei，QI Lin，CHEN En-qing，et al.Recognizing Human Emotional States Based on the Phase Information of the Two Dimensional Fractional Fourier Transform［J］.Lecture Notes in Computer Science，2010，6298(2):694-704.

［4］CEN Ling，Ser，ZHU Liang-yu.Speech emotion recognition using canonical correlation analysis and probabilistic neural network［J］.ICMLA，2008，137(21):85.

［5］HOTELLING H.Relations between two sets of variates［J］.Biometrika，1936(28):312-377.

［6］孙权森，曾生根，王平安，等.典型相关分析的理论及其在特征融合中的应用［J］.计算机学报，2005，28(9):1524-1533.

［7］RICHARD O D，PETER E HART D G S.Pattern Classification［M］.Wiley-Enterscience，2000.

［8］WANG Xiang-yin，ZHONG Yin-xin.Statistical learning theory and state of the art of SVM［J］.ICCI’03:55-59.