进化稳定策略在双重对称博弈中存在及证明
单长舟
(贵州大学理学院,贵州贵阳550025)
进化稳定策略在双重对称博弈中存在及证明
单长舟
(贵州大学理学院,贵州贵阳550025)
通过对进化稳定策略的刻画来对双重对称博弈中进化稳定策略存在进行等价证明,得出进化稳定策略存在的两个等价条件。
进化稳定策略;双重对称博弈;进化博弈
1 引言
进化博弈理论,顾名思义,是由生物学中关于进化思想与博弈理论交叉而形成的一个新分支领域,首先出现在生物学中。19世纪70年代,生态学家Maynard Smith和Price提出了进化博弈理论的基本均衡概念——进化稳定策略(ESS)。此后,生态学家Taylor和Jonker在考察生态演化现象时首次提出了进化博弈理论的基本动态概念——模仿者动态(Replicator Dynamics)。[1]至此,进化博弈理论有了明确的研究目标。至今关于进化博弈论及其应用的研究已有丰富的结果。[2,3]进化博弈假定给出博弈支付矩阵(Ak×kATk×k),用支付矩阵Ak×k描述进化博弈,从群体中随机抽取2个个体进行博弈。纯策略集合记为S={1,2,…n},群体中采取的第i个纯策略的比例xi表示第i个纯策略的概率,记表示所有混合策略的集合。博弈方1采取策略x∈△,博弈方2采取策略y∈△,支付分别为xTAy,xTATx。当二者交换位置但策略不变时,二者的支付分别为:yTAx=xTATy,yTAx=xTAy,即博弈与位置没有关系,用支付矩阵Ak×k就可描述进化博弈,当Ak×k=ATk×k时,博弈为双重对称博弈,也就是说随机个体不仅位置对称,而且收益一致,这对研究许多博弈的社会效率是非常重要的。本文研究双重对称博弈。
2 预备知识
定义2.1:x∈△是局部稳定的,如果它有一个邻域U使得对U中所有的y≠x,有
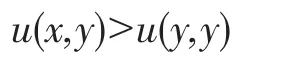
定义2.2:策略x∈△是局部严格有效的,如果它有邻域U使得对U中所有策略y≠x,有

定理2.1:x∈△为一个进化稳定策略(ESS)等价于存在x的邻域U(x),使得对任意x≠y∈U(x),有xTAx>yTAy。
定理2.2:当且仅当x是局部优越的,x∈△ESS。
定理2.3:如果一个状态是Lyapunov稳定的,那么它是稳态的。
定理2.4(自然选择基本定理):对任何双重对称性博弈而言,(x,x≥0),当且仅当x∈△0时等号成立。[2]
3 主要结果
对任意的混合策略x∈△,令Qx⊂△表示赋予所有纯策略正的概率的混合策略集合:

相对熵函数Hx:Qx→R,定义如下:
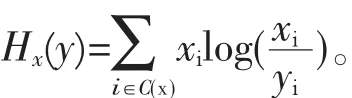
引理1:假设x∈△且y∈Qx,那么Hx(y)≥0,当且仅当y=x时等号成立。而且

定理3.1:对任何双重对称博弈,策略x∈△ESS当且仅当x∈△是局部严格有效的。
证明:假设矩阵AT=A,并令x∈△。对任何y≠x和,,

由于u是线性的,我们有由于u是对称的,所以。

局部严格有效与x的局部优越性有如下事实:当且仅当z≠x到x的距离在范围内,y≠x到x的距离在范围ε内。由定理2.2知,命题得证。
定理3.2:对任何双重对称博弈,策略x∈△ESS,等价于x∈△在复制子动态中是渐进稳定的。证明:假设x∈△ESS,由定理2.2,存在x的邻域U使得对所有在△∩U的y≠x,有:

我们已经指出,函数Hx的定义域QX是x的一个相对邻域,因此根据引理1,Hx是邻域V=Qx∩U上的复制子动态的严格局部Lyapunov函数。准确地说,Hx:V→R+是连续可微的,当且仅当y=x有Hx(y)=0且x(y)<0,∀y∈V。由定理2.3得知,策略x是渐进稳定的。
由定理3.1知,现在只需由x∈△在复制子动态中是渐进稳定的推出x∈△是局部严格有效的,进而得出策略x∈△ESS。如果x∈△是渐进稳定的,那么它有每个邻域U使得ξ(t,y)t→∞→x对U中所有的初始状态都成立。由定理2.4,我们有u(y,y)<u(x,x)对所有的y≠x都成立,进而此定理得证。
[1]Bomze,I.,and J.Weibull.Dose Neutral StabilityImply Lyapunov Satability[J].Games and Economic Behavior,1996,(11):173-192.
[2]WEIBULL J W.Evolutionary Gan1e Theory[M].Hayward,USA:MIT Press,1995:45-110.
责任编辑:胡德明
Abstract:This paper proves the existence of evolutionary stable strategy in two-ford symmetrical games by the characterization of evolutionary stable strategy,and then obtains two equivalent conditions for the existence of evolutionary stable strategy.
Key words:evolutionary stable strategy;two-ford symmetrical game;evolutionary game
The Existence and Proof of Evolutionary Stable Strategy in Two-ford Symmetrical Games
Shan Changzhou
(College of Science,Guizhou University,Guiyang550025,China)
O225
A
1672-447X(2012)03-0006-002
2011-11-07
单长舟(1987-),安徽宿州人,贵州大学理学院硕士研究生,研究方向为非线性分析及应用。

