地图矢量数据拓扑关系生成算法

徐 立，孙 群，杨 帅，徐 振

（1.信息工程大学测绘学院，河南郑州450052；2.北京大学地球与空间科学学院，北京100871；3.66240部队，北京100042）

地图矢量数据拓扑关系生成算法

徐 立1，孙 群1，杨 帅2，徐 振3

（1.信息工程大学测绘学院，河南郑州450052；2.北京大学地球与空间科学学院，北京100871；3.66240部队，北京100042）

拓扑关系的建立是地图矢量数据管理和更新的重要内容。在综合多种典型拓扑算法优点的基础上，详细描述了拓扑关系生成算法的主要过程，并在线要素互相交断链、结点匹配和特殊情况处理等方面对算法进行了改进。最后以1∶25万济宁市地形图数据进行了实验，结果表明该算法在效率方面优于传统算法。

拓扑元素；拓扑关系；线要素互相交断链；结点匹配；多边形追踪

地图图形数据的拓扑关系是对地图矢量数据进行空间查询、分析和质量检查等操作的基础［1］。拓扑关系生成算法主要包括3方面的内容：线要素互相交断链、结点与弧段间关系的建立、弧段与多边形间关系的建立。在处理大量数据的情况下，传统算法在线要素互相交断链过程中效率会明显降低；在建立结点与弧段间关系的过程中，传统算法往往无法科学地匹配不同精度的结点；另外，由于地图矢量数据较复杂，在建立弧段与多边形间关系的过程中有时会出现一些特殊情况，传统算法并没有合理地处理这些特殊情况。针对以上不足，结合现有地图矢量数据的特点，本文对传统的地图矢量关系生成算法做出了相应的改进。

1 拓扑元素的分类及地理意义

拓扑元素与空间要素并不是一一对应的关系。按照拓扑学原理，地图要素中的拓扑元素主要有3种基本类型：结点、弧段和面域［2］。

（1）结点。两条或两条以上弧段的连接点称为结点，一条闭合弧段的首尾接点或一条悬挂链的端点也可称为结点［3］。结点可以有实际地理意义，如道路中的交叉口、桥梁和界碑等；也可以无实际地理意义，如湖泊边线上的结点。

（2）弧段。两结点间的有向线段称为弧段［3］。弧段一般都具有实际意义，如道路、管线和面状河流湖泊的边线等；但在某些特殊情况下也可能没有实际意义，如面状要素的强制闭合线。在弧段的定义中，弧段是带有方向性的，但其对应的空间要素可能并没有方向性，如一般的公路（单车道公路除外）没有方向性。方向对于用来构建面域的弧段是有作用的，图1中湖泊a的边线是顺时针方向，岛屿b的边线是逆时针方向，在计算湖泊面积时，岛屿b的面积会出现负值。

图1 弧段的方向性Fig.1 Directions of the arcs

（3）面域。面域是指由一条或若干条弧段构成的闭合多边形［3］，每个面域都有一个内点（面域内的任意一点，承载面域的属性信息）与之相对应。绝大多数面域具有实际意义，如面状河流与湖泊、行政区和面状居民地等。

依据以上不同拓扑元素的地理意义，可以在拓扑数据预处理时自动筛选需要参加拓扑的元素。

2 算法的主要步骤

目前一般采用自动方式生成地图数据拓扑关系，首先对需要参加拓扑的数据进行预处理，再根据左转算法（通过判断邻接弧间的内角）和基于图的理论确定拓扑关系［4］。拓扑关系处理流程如图2所示。

在地图矢量数据中，只是部分要素层的部分要素需要参加拓扑，以1∶25万地形图的居民地层为例，只有由面属性决定的边线、图边强制闭合线、图幅内强制闭合线和街区边线需要参加拓扑［5］。因此在拓扑关系构建前，需要建立一个拓扑控制表，依据该表对初始数据进行筛选，以确定需要参加拓扑的要素。每个参加拓扑的要素层必须包含相应的拓扑控制表，每个参加拓扑的要素必须包含编码信息和精度等级信息。每种要素（以编码区分）都有一个精度等级，如省道比一般的县道等级高，在进行结点匹配时，若省道相关的结点与附近县道相关的结点在空间位置上发生冲突，则以省道相关的结点坐标为准。

图2 拓扑算法处理流程Fig.2 The process of the topological algorithm

2.1 线要素互相交断链

在采集地图数据时，为节省时间，可能将几条相连的弧段作为一条线要素输入，这样可能导致弧段之间相交。这种情况是不允许的，因为在弧段的定义中规定：弧段之间除了结点外不能有其它的公共点［6］。因此，需要对参加拓扑的线要素进行互相交断链处理。

2.1.1 线要素格网索引的建立 一幅地图矢量数据中，线要素数量最多，若对所有参加拓扑的线要素两两求交，势必降低算法效率。从全局角度考虑，大部分情况下线要素并不相交，这时可以将地图区域分为M×N个矩形子区域。由于有可能出现相交点落在线段延长线上且交点在线段某端点附近的特殊情况，这时两条线段实际上可能相交，但两条线段却又处于相邻的两个网格区域，则无法对两条线段进行相交处理，所以必须对网格进行适当的外扩处理，所生成的网格宽度w和高度h公式如下：

其中：Xmax、Xmin、Ymax、Ymin为图幅的外接范围，D为结点匹配误差，2D为网格扩充的长度。

2.1.2 线要素间的互相交断链 线要素格网索引建立完毕后，针对每个格网中的线要素进行互相交断链处理，算法如下：设网格线要素链表为Link，任意线要素为Li，n为Link包含的线要素个数，从链表Link中取出第一个线要素，并设置为当前要素L；将线要素L依次与后面的线要素Li（1＜i≤n，i为整数）求交。

（1）判断L是否已求交或是否有效，若已求交或无效，则转入步骤3；判断L的ID是否与Li的ID相同，若相同，则转入步骤3；判断L和Li的外接矩形是否相交，若不相交，则转入步骤3。

（2）将L标记为已求交，并依次取出Li中包含的线段，求出它们与L的交点。若其中一条线段Li与L产生交点，将Li标记为已求交，如图3所示：L与Li中的线段AB相交，产生交点P1、P2、P3。对于其它特殊情况还需另行处理：如图4中交点P1刚好与折线L的端点重合，此时生成3个线要素；根据交点对应于Li中的线段号，将交点重新排序为：P1、P2、P3。

（3）在Link中，取出当前线要素的后一个线要素，若不为空，将该要素设为当前要素L，转入步骤2，反之转入步骤4。

（4）建立新链表Link2，重新遍历链表Link，若线要素有效，则将要素加入链表Link2，据此生成的新链表Link2即为线要素互相交断链结果。

2.2 结点与弧段间关系的建立

线要素进行互相交断链处理生成的数据是孤立的弧段和结点，必须进一步通过结点匹配的方法建立结点与弧段之间的关联关系，同时也为弧段与多边形间关系的建立奠定了数据基础。

2.2.1 点要素格网索引的建立 建立结点与弧段间关系之前，除了要读入参加拓扑的结点要素（有实际意义的点状要素），还需加入弧段的首、末结点［7］。这里将结点分为两种类型：有实际地理意义的结点要素；没有实际地理意义且属于某一弧段的结点。类似于线要素的自相交断链算法，为了提高算法效率，必须对结点要素建立网格索引，此过程中只需判断结点是否落入特定的网格即可。另外，每个网格区域必须往外扩张2D（D为结点匹配容差）大小的范围，以防止相邻网格间出现结点漏匹配的情况。

2.2.2 结点匹配 结点匹配主要有两个作用：一是将距离在阈值D范围内的结点合并为一个点，当所有结点的精度等级相同时，可将其平均位置设为新结点的位置，否则，将等级最高的结点的位置设为平均位置；二是生成弧段与结点之间的拓扑关系。由于每个索引网格采用的算法都一样，所以下述结点匹配算法主要是针对单个索引网格，主要步骤如下：

（1）对网格内所有的结点排序。首先在x方向上对结点排序，然后在y方向上对结点排序，则点位相近的结点排至一起，这时只需对排序后的结点进行一次循环操作，便可找出位置相同或相近的结点，从而减少了比较次数。另外，对x和y两个方向的结点进行排序，可以避免结点间仅在某一方向距离很小而带来的干扰。

（2）排序后结点的处理。1）从排序后的链表中取出第一个结点，并设为当前结点。2）依次取出后面的结点，与当前结点进行比较，若后面结点不为空且两点间的距离小于等于匹配限差D，则将两结点作为一组；若两点间的距离大于匹配限差D，则计算点组中的结点数，结点数大于1则转入步骤3，反之转入步骤5。3）找出点组中所有结点的关联弧段，将其中的关联结点（首结点或末结点）设为新结点P（X，Y），并将这些弧段设为新结点的关联弧段。4）将点组中具有实际意义的结点坐标设为（X，Y），删除点组中没有实际意义的结点。5）取出下一个未比较的结点，若该结点不为空，则将该结点设为当前结点，转入步骤2；否则，结点与弧段的拓扑关系初步建立完毕，转入步骤6。6）依次遍历每个结点，将伪结点删除。在地图矢量数据中，若1个二链结点所关联的两条弧段属性完全相同，那该结点为伪结点，即所关联的两条弧段可以合并成一条弧段；若1个二链结点所关联的两条弧段属性部分相同，则该结点不是伪结点。例如，有一个结点A，在A处只连接沥青路L1和水泥路L2，因L1和L2道路性质不同，不能合并成一条道路，结点A则不是伪结点。伪结点的处理主要分为3步：将两条关联弧段合并为一条弧段；若结点有实际地理意义，则将结点修改为一般地理点要素，否则删除该结点；删除原来的弧段。

2.3 弧段与多边形间关系的建立

弧段与多边形关系的建立也称为面域构建，该过程是拓扑关系生成算法的最后阶段，其主要作用是根据结点与弧段的关联关系、多边形与面域点的包含关系和多边形之间的包含关系，生成简单多边形实体和复合多边形实体（如含有多个岛屿的湖泊）。算法主要分为多边形追踪和面域点与多边形关系的确定两个过程，前者是根据结点与弧段间的关联关系构建多边形，后者是在前者的基础上确定面域点与多边形的对应关系。

2.3.1 多边形追踪 多边形追踪算法的基本思路是：首先以数据中任意一条弧段为初始弧段，以初始弧段的首结点或末结点为初始结点，找出初始结点的所有关联弧段；然后以关联弧段中方向角最小的弧段为后续弧段，并将后续弧段的另一端点作为后续结点，再以上述方法进行循环追踪，直至满足追踪条件，则停止本次追踪。

对于大多数图形而言，每个多边形都可根据上述思想构建，但必须考虑以下两种特殊情况（图5）：若以图5a所示方向进行多边形｀追踪，在结点A处可能存在一条闭合弧段b（单独构成一个多边形），本次追踪可能在A点提前结束；此时需要重新回到A点，删除弧段b，以弧段c为后续弧段，继续向下追踪。以图5b所示方向进行多边形追踪，在结点A处下一个弧段是c，但是c以后的弧段都不能构成多边形，如果继续向下追踪，则会提前结束追踪。此时追踪的顺序为：先追踪到弧段d，发现没有后续弧段，则退回至结点B；追踪到弧段e，再次退回至结点B；然后继续退回至结点A，直至构成一个多边形。

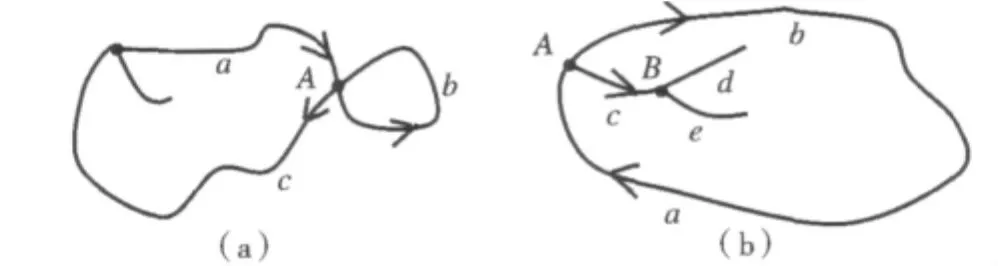
图5 多边形追踪特殊情况Fig.5 The exceptive instances of polygon tracking

2.3.2 面域点与多边形对应关系的确定 面域点与多边形之间可能存在多对多的关系，即一个面域点可能落入多个多边形内，一个多边形可能包含多个面域点，所以必须确定面域点实际与哪个多边形对应，以保证面域点与多边形之间的一对一关系，具体过程不再赘述。

3 实验分析

本文以1∶25万济宁市地形图的交通层和居民地层为实验数据，采用逐步增加拓扑要素的方法比较了传统拓扑关系生成算法和本文拓扑关系生成算法在执行效率上的差异，结果如表1、表2所示。

表1 交通层拓扑生成实验Table 1 Topological data generation for traffic layer

表2 居民地层拓扑生成实验Table 2 Topological data generation for habitation layer

表1中，交通层数据主要用来生成道路拓扑网，算法的耗时与参加拓扑的弧段总数呈正相关，因此实验主要对比两种算法建立结点与弧段间关系的效率。可以看出，当弧段总数较小时，两种算法的时间相差不大；但随着弧段总数的增加，两种算法的时间差越来越大，说明在大数据量情况下，本文算法能够明显减少拓扑关系生成的时间。

表2中，由于不需要对居民地数据进行线要素互相交断链处理，算法的耗时与参加拓扑的面域总数呈正相关，因此实验主要对比两种算法追踪多边形的效率。可以看出，随着面域总数的增加，两种算法的时间差不断增大；但当面域总数增至一定数量时，两者的时间差比较稳定，但本文算法的效率一直优于传统算法。

4 结论

拓扑关系生成算法主要包括线要素互相交断链、结点匹配和多边形追踪等子算法。本文对以下方面进行了改进：1）利用要素编码控制表的形式筛选参加拓扑的要素，并对每类要素设置精度等级，使结点匹配时的点坐标拟合更科学；2）根据属性信息对伪结点进行自动处理，对结点和弧段建立网格索引，提高了算法的运行效率；3）对算法中出现的多种特殊情况进行了处理，提高了算法的稳定性。

［1］ 华一新，吴升，赵军喜.地理信息系统原理与技术［M］.北京：解放军出版社，2001.30.

［2］ 谢露蓉.地图图形数据拓扑关系的建立［J］.测绘科学，1999，3（2）：36－41.

［3］ 赵国成.基于Microstation的扫描矢量化软件的研制［D］.信息工程大学，2004.53－54.

［4］ 陈春，张树文，徐佳芬.GIS中多边形图拓扑信息生成的数学基础［J］.测绘学报，1996，3（4）：266－271.

［5］ 刘海砚.数字地图制图原理与技术［M］.北京：解放军出版社，2006.62.

［6］ 程双伟.GIS中拓扑关系的建立与更新［D］.信息工程大学，2002.16.

［7］ 李丽丽.基于拓扑关系的导航电子地图增量更新关键技术研究［D］.吉林大学，2009.30－31.

Abstract：The establishment of topological relationship is essential to map vector data management and updating.Based on the advantages of multiple topological algorithm being integrated，the main process of topological was introduced detailedly.The topological algorithm was modified at the aspects of line feature intersecting，node matching and area building.Finally，an experiment was tried on the 1∶250 000 scale topographical map data for Jining.It indicated that the efficiency of topological algorithm could be improved compared to the traditional algorithm.

Key words：topological element；topological relationship；line feature intersecting；node matching；polygon tracking

Topological Algorithm for Map Vector Data

XU Li1，SUN Qun1，YANG Shuai2，XU Zhen3
（1.Institute of Surveying and Mapping，Information Engineering University，Zhengzhou 450052；2.School of Earth and Space Sciences，Peking University，Beijing 100871；3.66240 Troops，Beijing 100042，China）

P283

A

1672－0504（2012）04－0018－04

2012－01－07；

2012－03－12

国家自然科学基金项目（41071297）

徐立（1985－），男，博士研究生，主要研究领域是空间数据模型和数字制图技术。E－mail：xuli＿1985＠yeah.net