平面三自由度欠驱动机器人轨迹跟踪控制*

胡 毅，余跃庆

(北京工业大学机械工程与应用电子技术学院，北京 100124)

平面三自由度欠驱动机器人轨迹跟踪控制*

胡 毅，余跃庆

(北京工业大学机械工程与应用电子技术学院，北京 100124)

对平面3R欠驱动机器人的轨迹跟踪控制问题进行了研究，该机器人有两个驱动关节和一个自由关节。利用拉格朗日方程建立了该机器人的动力学模型。依据该动力学模型，分析了该类机器人的特点，并设计了一种模糊控制方法。控制系统根据模糊逻辑控制器输出量得到主动关节的控制力矩。利用主动关节和被动关节之间的动力学耦合作用，控制被动关节，以实现机器人末端的直线轨迹跟踪任务。采用该控制方法，对控制过程进行了数值仿真，结果表明该方法具有可行性。

欠驱动机器人;轨迹跟踪;模糊控制;动力学耦合

0 引言

欠驱动机器人是一类含有被动关节，驱动关节数目小于关节总数，能用较少的驱动装置完成复杂任务的机械系统，驱动的减少使系统总质量减少，同时又节省了能源，特别是在太空和水下机器人系统以及仿生机器人等研究领域具有广阔的应用前景，因此此类机器人越来越成为人们研究的热点［1-4］。

欠驱动系统本质是非线性系统，满足Brockett条件［5］，即不存在光滑的状态反馈控制律使系统稳定在平衡点上，因此欠驱动系统的控制问题要比一般的非线性问题更加复杂和困难，必须设计新的工具和方法。目前，还没有通用的理论来研究欠驱动机器人的运动规划和控制。Oriolo等［6］论证了含有自由的动力学约束一般情况下是不可积的，因此为二阶非完整系统。De Luca［7-8］等研究了第一个关节受驱动，而第二个关节为被动的2R、PR机械臂的稳定性问题。Arai［9］等利用构造轨迹方法证明了平面3R欠驱动机器人是可控的，并运用反馈控制策略实现对平面3R机器人的位置控制。何广平［10］等提出了两种欠驱动机械臂位置控制的谐波函数控制方法。刘庆波［11］等针对欠驱动机器人的运动控制问题，提出了一种基于遗传算法的模糊控制新方法。以上文献主要集中在被动关节的位置控制上。在实际应用中，欠驱动机器人的末端轨迹控制是十分重要的，因此有必要在相关方面做更深入的研究。

本文以末端关节是欠驱动的平面3R机器人为研究对象，对其末端轨迹跟踪控制问题进行研究，根据欠驱动系统的特征并基于模糊理论设计一种控制方法对其进行运动控制。在仿真层面实现规划的直线轨迹以验证控制方法的可行性。

1 动力学模型

平面3R欠驱动机器人结构如图1所示。第1、2关节(实心圆)为主动关节，第3关节(空心圆)为被动关节。各杆是匀质杆，因此视各杆质量集中在杆的中点。而且由于本文研究的是平面机器人，故不用考虑重力项。通过Lagrange方程，可以得到动力学方程:

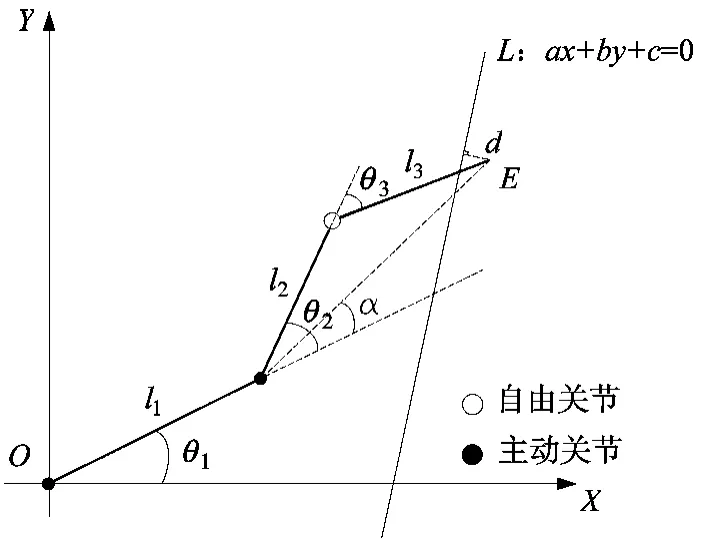
图1 平面3R欠驱动机器人

式中，M为系统的惯性矩阵，h为哥氏力和离心力项，f为阻尼项，θ为关节角度，τ为关节力矩矩阵;其中，h、f与角速度及其乘积有关。将主动和被动关节分离，式(1)可以得到如下形式:

由式(2)可知，欠驱动机器人在模型上与全驱动机器人相似，但因被动关节无转矩输入，所以其加速度约束具有不可积特性，即运动受二阶非完整约束，不能直接从运动学角度控制被动关节的运动。但是，主、被动关节的加速度之间存在耦合关系，因此可以通过控制主动关节来间接地控制被动关节。此时关节的运动与输入转矩有关，所以应从动力学角度来实现欠驱动机器人的控制任务。

2 控制方法

如图1所示，E为机器人的末端，L为规划的直线轨迹。d为E到直线L的距离，同时也将d视为误差值，并规定对于L而言，原点O所在一侧的点到L的距离为负，剩余的点到L的距离为正。α为关节2和末端E之间的连线与杆1的夹角，是机器人的位形参数。

首先，规定关节角速度、角加速度、关节控制力矩(或控制电压)逆时针方向为正，顺时针方向为负。轨迹跟踪的控制思路为关节1以规划的角速度运动，同时通过主动关节2和被动关节3之间的动力学耦合作用控制关节2和关节3的角度，最终实现末端跟踪规划的轨迹，整个过程被动关节3完全自由。在这个过程中，主动关节1的加速和减速均会对被动关节3产生动力学耦合作用，此耦合作用被视作是对关节3的干扰，可以通过对关节2实时控制予以消除。因为关节1是按照规划的角速度运动，所以只要保证d=0，就能使得末端跟踪指定的直线轨迹。控制原理框图如图2所示。

图2 直线轨迹控制原理框图

图2中FLC表示模糊逻辑控制器，τ表示关节2的控制力矩(或控制电压)。其具体过程为:主动关节1按照规划的角速度进行运动，同时将d和α作为输入变量反馈给FLC，通过FLC规则得到作用于关节2的输出变量τ，再经动力学耦合作用控制被动关节3的运动，使末端跟踪期望轨迹。

下面分析圆弧轨迹的FLC模糊逻辑控制器规则的具体形式。

α是机器人的位形参数，可以根据其值将位形分为两种情况;当α≤0时，记为Flag=1;当α≥0时，记为Flag=2。根据实际手动控制经验可以总结出模糊控制规则，如表1所示。表1中，{NB、NS、ZO、PS、PB}为隶属度函数模糊语言变量值。

表1 FLC模糊控制规则表

从表1中可以看出，输出量τ与输入量d在各自论域上均分成5个模糊集合。当Flag=1时，τ值的正负与d的相反;当Flag=2时，τ值的正负与d的相同。

依据表1，并考虑到实时计算量，可以将输入量、输出量的模糊化与解模糊化进行简化，得到的输出控制量τ的简化形式为:

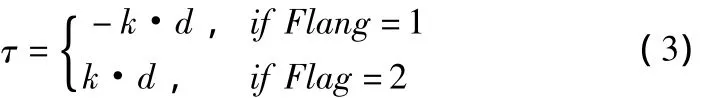
式中k为模糊控制量系数。

依据该控制策略，在直线轨迹跟踪控制仿真中，需要根据结果，不断调整k值，已达到最好的控制效果。

3 数值仿真

仿真对象为图1所示的平面3R欠驱动机器人，并考虑关节摩擦力对运动的影响，该摩擦力采用粘性摩擦模型，模型如式(4)所示:

其中f为摩擦力矩，μ为粘性摩擦系数为关节角速度。仿真的参数如表2所示。

表2 仿真参数

表中质量单位为 kg，长度单位为 mm，mc1、mc2和mc3分别为各杆的质量，m1、m2和m3分别为各关节的集中质量，l1、l2与l3分别为各杆的长度;μ1与 μ2分别为主动关节1与主动关节2的摩擦系数;μ31与μ32分别为被动关节3顺时针转动与逆时针转动时的摩擦系数。

机器人的操作任务是跟踪直线y=x-650，起始点为 P0(0，-650)，终点为 Pd(442，-208)，轨迹长度为625，坐标单位与长度单位均为mm;在起始位置时，θ1=-90°，θ2=0°。设定关节 1 以变速运动到30°，关节1的角加速度如式(5)所示:

式中时间t的单位为秒(s)。

在仿真过程中，依据上述控制策略，经过不断摸索及反复调节，最终设定控制量系数k=14.5，以0.01s为一个周期读取各个关节角度值，以及机器人末端坐标和误差等其他数据，依据这些结果可以绘制如下数据曲线。

图3显示了末端实际轨迹与末端期望轨迹的对比，图4为误差值曲线，图5表示了三关节角度变化。图3显示的末端实际轨迹说明在经过开始的小幅振荡后，末端逐渐收敛至期望的轨迹，比较精确地完成了操作任务。

图3 末端轨迹

由关节1的角加速度可知，关节1在3.9s时角速度和角加速度变化最大，由此造成的对被动关节3的干扰最大;因此可从图4、图5看出，误差在3.9s达到最大，此时关节2、关节3由于耦合作用，角度变化比较剧烈;系统在经过短暂调整后逐步收敛进入稳态阶段，并使误差值收敛到期望值，说明通过对主动关节2的控制，较好地解决了主动关节1对被动关节3产生的干扰。

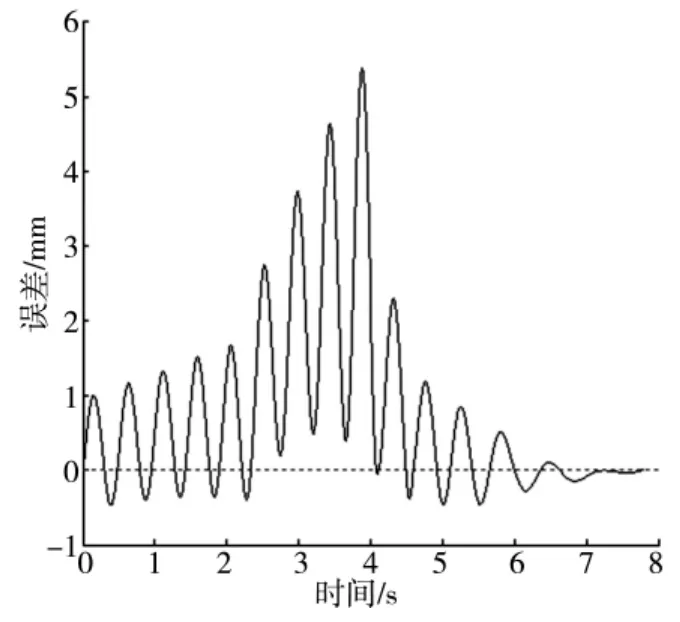
图4 误差

图5 三关节角度

表3为仿真结果的误差分析，从表中可知在整个运动过程中，误差都在可接受范围之内。

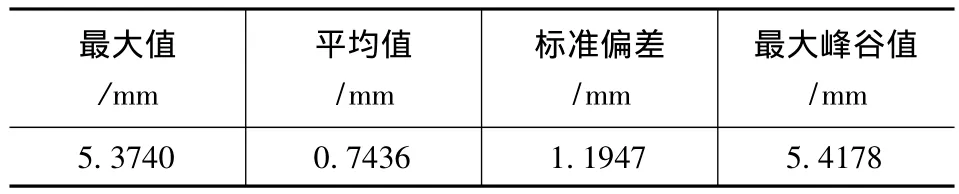
表3 仿真结果误差分析

4 结束语

本文研究了平面3R欠驱动机器人的轨迹控制问题。运用模糊控制理论，设计了适用于二阶非完整系统的控制方法，该方法具有规则简单、实时计算量小及参数容易调节等优点。仿真结果表明，平面3R欠驱动机器人能完成直线轨迹跟踪，验证了控制方法的有效性及智能控制的优越性，为今后所要研究的复杂曲线跟踪等问题提供有效的控制策略及方法。

［1］Mahhndraker A D，Rao S，Banavar R N.Point-to-point control of a 2R planar horizontal underactuated manipulator［J］.Mechanism and Machine Theory，2006，41(7):838-844.

［2］Mahhndraker A D，Banavar R N.Reyhanoglu M.Controllability and point-to-point control of 3-DOF planar horizontal underactuated manipulators［J］.International Journal of Control，2005，78(1):1-13.

［3］Udawatta L，Banavar R N，Reyhanoglu M.Control of underactuated robot manipulators using switching computed torque method:GA based approach［J］.Soft Computing-A Fusion of Foundations，Methodologies and Applications，2003，8(1):51-60.

［4］Arai H，Kazuo T，Naoji S.Time-scaling control of an underactuated manipulator［C］//Proceeding of the 1998 IEEE International Conference on Robotics＆Automation.Leuven，Belgium:IEEE，1998:2619-2626.

［5］Brockett R W.Asymptotic stability and feedback stabilization，differential geometric control theory［M］.New York，USA:Birkaeuser，1983:181-191.

［6］Oriolo G，Nakamura Y.Control of Mechanical Systems with Second-order Nonholonomic Constrains:Underactuated Manipulator［C］//IEEE Conf.on Decision and Control.Brighton:IEEE，1991:2398-2403.

［7］Luca A D，Mattone R，Oriolo G.Stabilization of an underactuated planar 2R manipulator［J］.International Journal of Robust and Nonlinear Control，2000，24:181-198.

［8］Luca A D，Iannitti S，Oriolo G.Stabilization of a PR planar underactuated robot［C］//Proceeding of the 2001 IEEE International Conference on Robotics＆Automation.Seoul:IEEE Press，2001:2090-2095.

［9］Arai H，Tanie K，Shiroma N.Nonholonomic control of a three-dof planar underactuated manipulator［J］.IEEE Trans on Robotics and Automation，1998，14(5):681-695.

［10］何广平，陆震，王凤翔.平面三连杆欠驱动机械臂谐波控制方法［J］. 航空学报，2005，25(5):520-524.

［11］刘庆波，余跃庆，苏丽颖，等.基于遗传算法的平面欠驱动机器人模糊控制［J］.机械设计与研究，2008，24(5):42-46.

Trajectory Tracking Control of a 3-DOF Horizontal Underactuated Robot

HU Yi，YU Yue-qing
(College of Mechanical Engineering and Applied Electronics Technology，Beijing University of Technology，Beijing 100124，China)

A study of controlling the trajectory tracking of a 3R horizontal underactuated robot is investigated;the robot has two actuated joints and a free joint.The dynamic model of the robot is established with Lagrange equitation.Based on the dynamic model，the property of this kind of robot is analyzed;a fuzzy control method is designed.The control torque of the active joints is determined by the output parameters of fuzzy logic controller.Applying the dynamic coupling of the active joints and passive joint，the passive joint is controlled;the linear trajectory tracking of the robot is achieved.Using this control method，the course of controlling is simulated;the results show that the proposed method is effective.

underactuated robot;trajectory tracking;fuzzy control;dynamic coupling

TH121;TP24

A

1001-2265(2012)12-0082-03

2012-02-03

国家自然科学基金资助项目(50875002)

胡毅(1987—)，男，北京工业大学机械工程与应用电子技术学院硕士，研究方向为机器人控制等，(E-mail)emails_huyi@126.com。

(编辑 李秀敏)