一种切削力信号分析系统的开发及应用试验*

穆以东，赵 岭

(聊城大学汽车与交通工程学院，山东聊城 252000）

0 引言

现代切削加工正在向高速强力切削、精密超精密加工方向发展。机床切削力测量、处理和分析对切削刀具寿命、加工成本的估算以及提高加工精度具有重要作用，已受到现代机械制造企业的广泛重视。同时，在科学研究和工业生产中，需要采集的数据量越来越多，对数据处理的要求也越来越高。因此，采用先进的数据采集与处理系统，一方面能及时、全面地对数据进行真实有效的采集和储存，另一方面也能够对数据进行科学合理的分析和处理。所以，研制一款集采集与分析于一体、操作简便易行的信号采集与分析系统，不但能够大大缩短产品的生产时间，降低生产成本;而且能够给科学研究提供详实的数据，在研究过程方面起到一定的积极作用。本文自行设计了切削力信号采集与分析系统，并对实验结果进行了分析和处理;通过试验结果与切削力建模与仿真结果的比对，验证了本信号采集与分析系统设计的合理性和使用的准确性，对实际生产中切削力的控制具有一定的指导意义。

1 切削力信号分析系统的开发

测力系统的硬件组成如图1所示，主要由力传感器、信号调理器、数据采集与处理单元和显示设备等组成。力传感器将被测切削力转换为电信号;信号调理器对微弱电信号进行必要的处理，包括信号的放大和滤波等。数据采集与处理单元用于将模拟信号转换为数字信号，便于计算机分析;显示设备(如计算机等）将采集到的信号直观显示，易于对数据进行观察、分析和处理［1］。

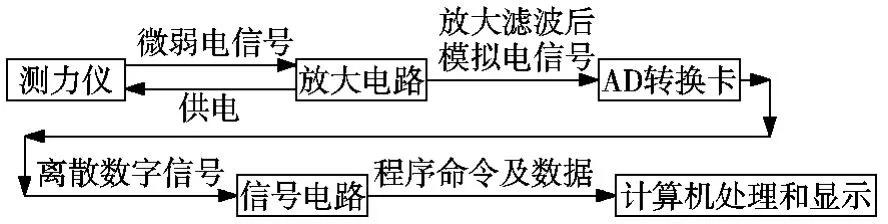
图1 测力系统硬件功能图

1.1 切削力测试系统的总体设计

本系统采用了软件开发平台LabVIEW模块化的设计方法［2］，即把所需要的各项集成起来作为一个模块进行编程，这样既简化了编程，同时还能使整个系统一目了然，非常直观。

测试系统的总体模块化设计如图2所示。

图2 测试系统总体模块设计图

1.2 参数设置模块

测试系统要求对采集信号的通道个数、采样频率、总的缓冲区的数目、每个缓冲区的采样点数等参数进行设置。对这些参数的综合设置可以调整合适的信号采集时间和总的采样点数。如图3所示，它们之间满足下面的关系:

共采集到的点数=频率×采集时间

共采集的点数=每个缓冲区采集点数×n个缓冲区

图3 参数设置模块前面板

1.3 数据采集模块

数据采集模块主要包括了信号采集和模数转换两个部分。数据采集在检测系统中占据了重要地位。因为只有把信号真实的采集进来，才有可能对数据进行分析处理，或者对于某些测控系统才能实现正确的控制。信号数据是实现正确控制的基础。

数据采集的任务就是将传感器采集的电压信号通过各采集通道然后经过数模转换转换成数字信号输入到计算机中，最后再实时显示出来，其示意图如图4所示。

图4 数据采集示意图

1.4 数据显示及输出模块

为了将经过上述数据采集模块采集得到的切削力信号能够直观、真实的显示出来，本系统采用了同时使用虚拟仪表和通道波形显示的方法，如图5所示。

图5 虚拟仪表面板和通道波形显示

2 切削试验及结果分析

2.1 试验条件

本实验所采用的采样频率为:1024Hz，而实验中采集的信号的频率最高也不超过500Hz，根据奈奎斯特采样定律［3］，采集时的采样频率不能低于所采集信号频率的2倍，因此，本设置能够采用。根据硬铝合金试样的切削性能，我们采用的主轴转速为1000rev/min，此速度基本符合实验条件的要求。进给速率设为30mm/min，由此计算出的刀具的每齿进给量约为0.015mm/s;本实验中刀具的旋转方向为顺时针。为了采样过程的清晰以及易于采样数据的比较，实验中走刀的方向设置为单向走刀方式。同时为了最大限度地减少切削振动对于采集的影响，本实验采用了顺铣的切削方式，即人为地把行切时刀具的走向设置为分别沿X、Y的负方向。在本实验中，采用了较大的纵向切削进给量，即2mm，以放大切削力的数值，使切削力变化的趋势更为明显，有效防止切削力信号被其他的噪声和振动信号所掩盖［4］。

中国提出的“一带一路”倡议秉持共商共建共享原则，不以获取能源资源和输出过剩产能为目的。但在共商共建共享原则的落实过程中，在一些具体合作项目中出现了“单向施惠”现象，即馈赠式贸易让步。“单向施惠”有利于提升合作意愿，但缺乏效率性、稳定性、可持续性，会导致一些国家对国际合作存在过高的期待，所谓的“期待”无法实现后国际合作可能会发生变更。因此，在“一带一路”建设过程中，沿线国家应努力营造更多人关注、更多人参与、更多人贡献、更多人受益的国际合作局面。

2.2 切削方式设计

本实验中，为了采集数据的多样化和方便数据的对比，采用了切削多个椭圆抛物面和采用不同走刀方式相结合的切削方法，即首先将一个长轴:16.67mm、短轴:13.34mm、长短轴比:5:4、深度:8mm的椭圆抛物面作为基准曲面，对其分别进行沿X、Y方向行切，利用事先调试、设置好的数据采集设备对三种不同的加工过程进行全程跟踪采集，并将数据存盘后利用分析系统进行分析。

图6 行切产生的椭圆抛物面

2.3 实验数据分析

2.3.1 基准椭圆抛物面沿X方向行切时的数据处理接近曲面最凹(Y=0.956）处的曲面段作为研究部分。此部分的采集波形如图7所示。

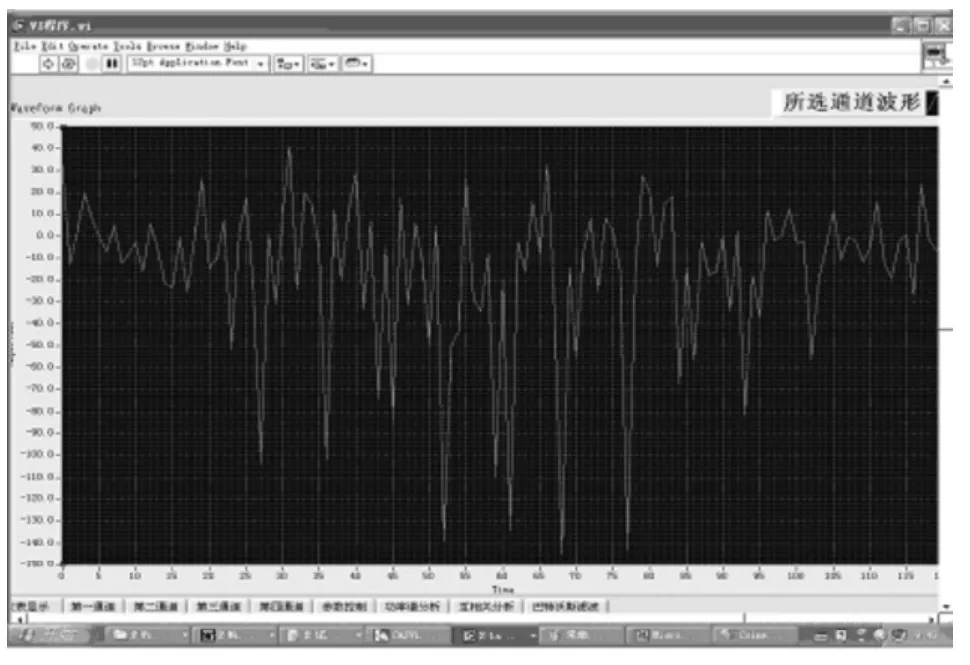
图7 基准曲面沿X方向行切X通道部分波形

然后，再将图8进行巴特沃斯滤波，所得图形见图8。

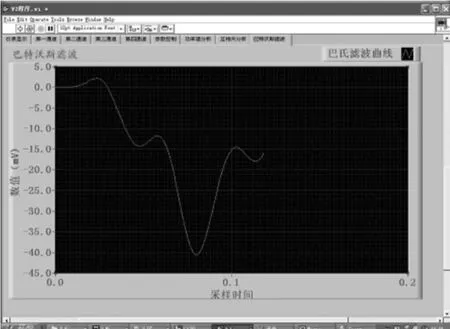
图8 Y=0.956段波形经滤波后的图形

同样采用相同的方法再作出Y=2.869走刀时的时域波形如图9所示。

由数学知识可知，对于椭圆抛物面来讲，Y=0.956处的曲面法曲率要比Y=2.869处的法曲率大。同时，从图8与图9比较即可以看出，Y=0.956处对应的切削力的数值也较Y=2.869处所对应的数值大。两种波形滤波后对比见图10。

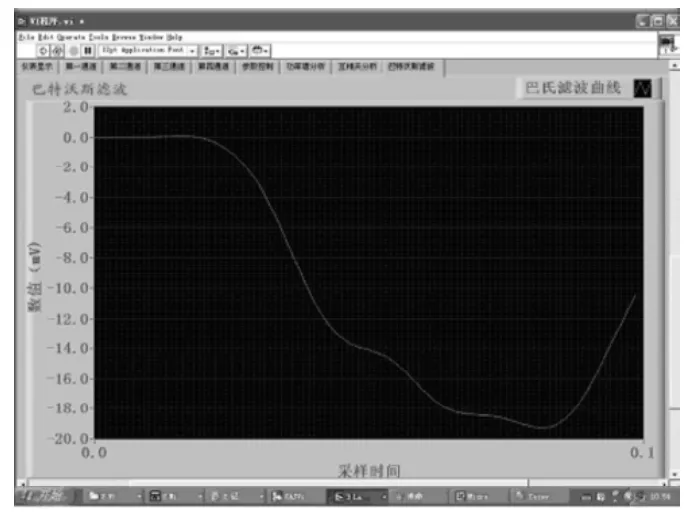
图9 Y=2.869段波形经滤波后的图形

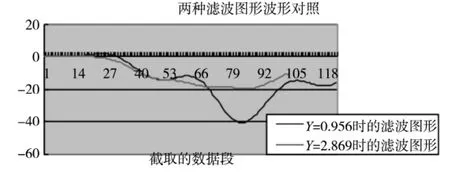
图10 两种滤波图形波形对照

2.3.2 基准椭圆抛物面沿Y方向行切时的数据处理

同理，可得出一次走刀波形(X=-1.963）

分别在此及其邻近的走刀路线(X=-3.927）上分别取点进行对照，方法同上。

图11 上述两段波形叠加比较的图形

很明显，可以得出与X方向行切时相同的结论。即沿Y方向行切时在同一走刀路线上越接近X=0处的Y方向的主切削力越大;同样，在方向相同的不同走刀过程中，越接近Y=0的路线的主切削力的数值及波动幅度也较远离者依次增大。

2.3.3 分别沿X和Y方向行切的切削力数值比较

选择一段一次走刀(X=1.965，Y=1.963）的数据进行对比，其图形如图12所示。

图12 基准椭圆抛物面沿X和Y方向行切时主切削力比较

从图12中可以明显地看出，沿Y方向行切时的切削力数值与波幅几乎总是大于沿X方向进行行切的数值。也就是说，在对曲面进行行切时，沿X方向行切的主切削力数值和波动幅度总是低于沿Y方向的。

2.3.4 曲面深度加深至原来的1.5倍后的曲面与基准曲面的比较

从图12中提取出部分具有代表性的一次走刀过程(Y=1.963）的数据进行分析，如图13所示。

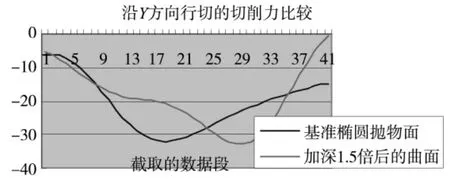
图13 沿Y方向行切时的部分数据比较

2.3.5 长短径比变为5:3后的曲面与基准曲面的比较

取出一次走刀(Y=1.963）的一段数据，同长短径比缩小为5:3的曲面在相同走刀过程中的数值进行比较，如图14所示。

图14 两图线沿Y方向一次走刀的切削力比较图

经对上述图形及表格的分析，可以明显地看出:深度加深1.5倍后的曲面(对应点处的法向曲率增大）沿X方向行切及沿Y方向行切时的主切削力均明显大于基准抛物面的;同样，长径比为5:3的曲面(对应点处的法向曲率增大）经两次走刀的主切削力也明显地大于基准抛物面的。

下图是利用切削微元法［5］对立铣刀的主切削力进行建模并依据Matlab［6］仿真后的铣削主切削力的图形如图15所示。

3 结论

由仿真图形和指标模拟数据可知，沿X或Y方向行切时，越靠近X或Y等于0的区域，亦即曲面法曲率越大的区域，铣削所产生的主切削力越大。经过与开发的切削力信号测试分析系统所得数据的比对可知，所得的结果与仿真结果基本上是吻合的。

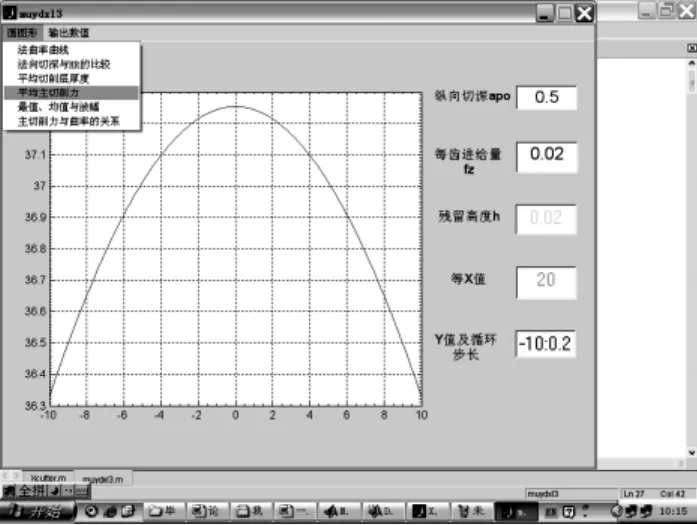
图15 某一切削状况下的主切削力仿真图形

本次理论建模所用的数学模型有其完整的科学性要求的，同时，周密的数学推导过程推理严密、逻辑符合条件，因此满足科学性的要求。此外，实验环节紧凑，实验条件设计合理，所得数据真实可靠，分析结果具有说服力。

总之，设计开发的切削力信号测试与分析系统，具有结构简单、成本低、用途广的优点，经过理论建模仿真与实验分析，充分证实了本切削力信号测试分析系统所得数据的真实性和可信度。因此，本系统能够在实际生产中得到广泛的应用，能够对切削力的测试及实验起到一定的指导作用。

［1］罗学科.动态多维力传感器的理论研究与实践［D］.北京:北京航空航天大学，1995.

［2］程学庆，房晓溪.LabVIEW图形化编程与实例应用［M］.北京:中国铁道出版社，2005.

［3］张超英，罗学科.数控加工综合实训［M］.北京:化学工业出版社，2003.

［4］姜彬，郑敏利，徐鹿眉.数控铣削用量多目标优化［J］.哈尔滨理工大学学报，2002，7(3）:67-70.

［5］姜彬.数控切削加工工艺参数优化的研究［D］.哈尔滨:哈尔滨理工大学，2001.

［6］李海涛，邓樱.Matlab 6.1基础及应用技巧［M］.北京:国防工业出版社，2002.