曲轴成品质量中心定心法及算法研究
黄继雄,易 勇
(武汉理工大学机电工程学院,湖北武汉 430070)
曲轴是发动机的关键零件之一,曲轴中心孔是曲轴加工过程中的定位基准和检验基准,其定心方法对后续工序的加工质量有较大影响[1-2]。笔者提出曲轴成品质量中心定心的概念,并依据曲轴以及曲臂毛坯重构的几何信息,对其中的关键问题,即预测曲轴成品回转质量中心轴线的算法进行了研究,为实现曲轴成品质量中心定位工艺奠定了基础。
1 曲轴成品质量中心定位工艺
曲轴加工时主要定位基准是中心孔,为了提高曲轴加工的质量,中心孔的加工方法不断改进,目前主要有几何中心法和毛坯质量定心法[3-5],但各自也有不足之处。
几何中心法对毛坯的质量要求比较高,打出的中心孔离散性较大,生产过程中会出现中心孔打偏、加工时动不平衡量大产生振动以及动平衡去重的质量超出配重扇形面的许可而造成工件报废等弊端。
现有的质量定心法,应称为毛坯质量定心法,需要在质量定心机上进行平衡,它能使曲轴毛坯的初始不平衡量减小,但是随着后续加工的进行,不平衡量会越来越严重,往往还需要进行再平衡。
成品质量中心法通过计算机视觉快速获取曲轴毛坯几何信息,进行三维重构,实现曲轴成品CAD模型与毛坯重构模型的最佳匹配[6-7],在满足一定匹配准则的前提下,预测曲轴成品的质量中心,并以其作为定位基准中心。其优点主要有:
(1)曲轴随着加工的不断进行,不平衡量越来越小,加工完毕,不平衡量达到最佳状态,理论上不需要再进行去重平衡。考虑到由于制造过程的误差会造成少量的动不平衡,若其在允许范围内,则不需要去重动平衡;即使需要做去重动平衡,其去重的质量也比较小。
(2)通过软件编程输出中心孔的位置坐标值,准确且不易打偏,相对于质量定心法成本低。
(3)省去动平衡工序,可改善曲轴内力平衡,节省工时,在曲轴大批量生产中更具有经济意义。
2 曲轴及曲臂毛坯的重构
逆向工程技术是指用一定的测量手段对实物或模型进行测量,并根据测量数据通过三维几何建模方法重构实物CAD模型的过程。笔者使用海克斯康的Global系列桥式三坐标测量机测量曲轴毛坯的点云数据,使用三维软件Catia V5中的逆向模块[8],通过三维重构获取曲轴毛坯以及曲臂部分的几何信息,并生成曲轴及曲臂毛坯的三维模型。
实验曲轴为四缸铸造曲轴毛坯件,如图1所示。三坐标测量机的测量精度达到 ±0.5 μm。为提高测量速度,将铸造毛坯的分型面看作对称面,测量曲轴的上部分结构,简化部分规则表面的测量,生成的点云图如图2所示。

图1 曲轴毛坯图
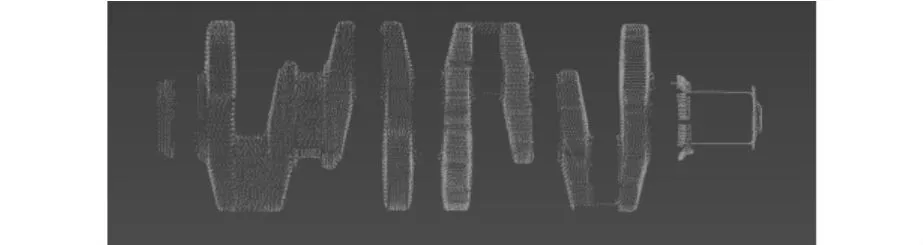
图2 曲轴毛坯点云图
3 曲轴成品质量中心定心算法
曲轴是一个不规则的复杂零件,其回转质量中心轴线是唯一的。曲轴加工过程中主要加工表面是轴颈,由于该定心工艺方法可以省去动平衡工序,作为去重平衡处理的曲臂可以看作非加工表面。故可有以下假设:
(1)成品曲轴的各个轴颈,是具有一定尺寸的规则圆柱体,其质量回转中心为其几何中心。
(2)成品曲轴的曲臂部分,是非规则表面,不需要加工,其质量回转中心只能经过动平衡计算得到。
因此,当曲臂满足动平衡时,其质量回转中心轴线一定存在,在此轴线基础上重构各个规则的轴颈,则曲轴成品也一定会满足动静平衡。故曲轴成品质量中心定心法的关键是预测成品曲轴的质量中心,即可转化为预测曲臂的质量中心轴线。其算法流程如图3所示。
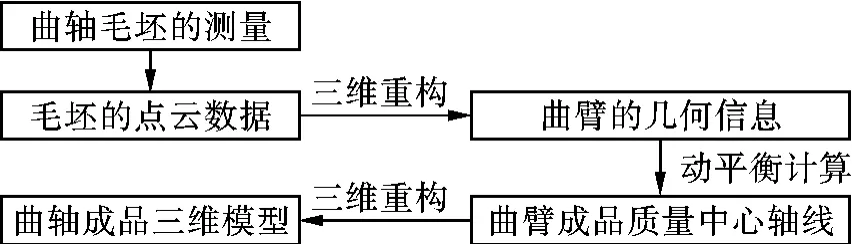
图3 曲轴成品质量中心算法流程图
3.1 曲臂的网格离散化
曲臂毛坯的各个曲臂是分离的,在具有较强网格划分功能的Hypermesh中进行网格化,然后导入到ANSYS中,利用命令流查询并输出曲臂的各个离散单元体积以及单元质心坐标值[9],保存为Excel格式。
网格单元采用Solid185单元,铸铁毛坯件密度为7.25×10-6kg/mm3,划分完成后,统计得到有17699个单元。曲臂离散网格如图4所示。
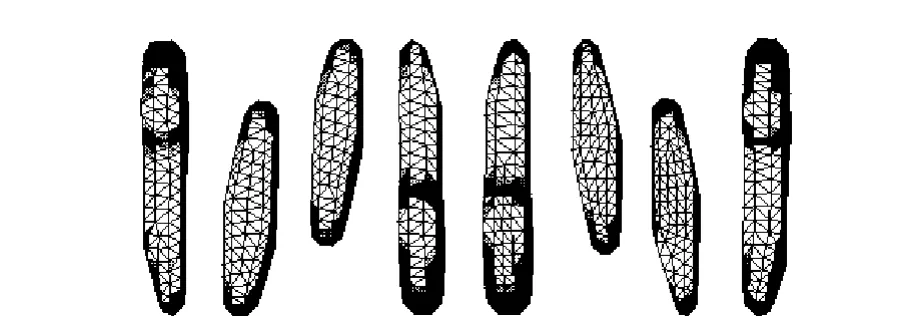
图4 曲臂离散网格图
3.2 数学模型的建立
(1)理论基础。根据动平衡理论,当回转体的惯性力系主矢和惯性力系主矩同时为零时,则该回转体处于动平衡状态。对于曲柄毛坯件,其轴向尺寸比较大,由于质量不是分布在同一回转平面内,必须进行动平衡计算。
选定曲轴毛坯的两个轴端面作为平衡基面Ⅰ和Ⅱ,将每个质点产生的离心惯性力分别分解到两个平衡基面内,只要两个平衡面内合力分别为零,则曲臂处于动平衡状态。因此,为简化计算,建立一个动态坐标系,使得新坐标系的原点固连在曲轴毛坯的某一轴端面上,通过新坐标系的变换使得曲臂的所有离散单元对Y'轴满足动平衡计算,则Y'轴即为曲臂的质量中心轴线。其计算示意图如图5所示。
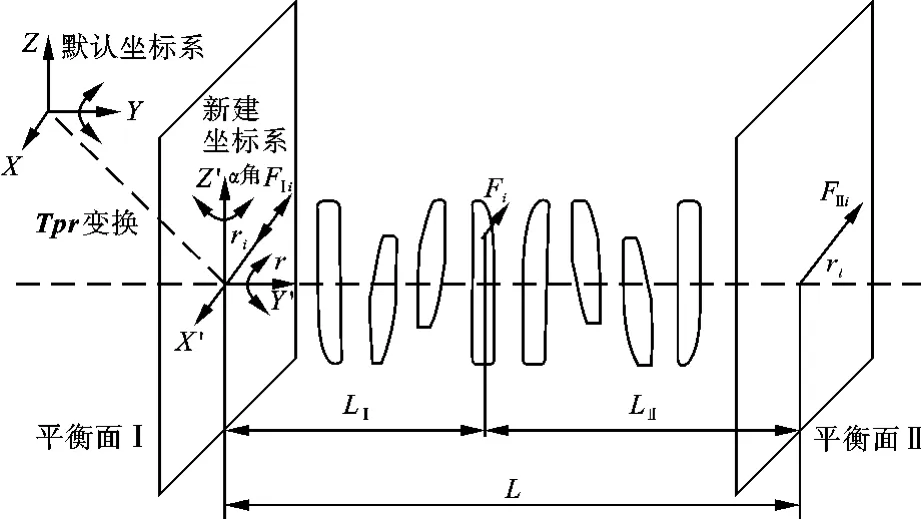
图5 曲臂质量中心轴线计算示意图
(2)坐标变换。在新坐标系中计算曲臂的动平衡时,离散单元的质心坐标也要随之变化,因此通过建立两坐标系之间的变换矩阵,使得新坐标系的Y'轴为曲臂的质量中心轴线。假设新坐标系的原点为O',在原坐标系下的坐标值为(X0,Y0,Z0),根据曲臂毛坯重构中建立的对称性,Z0为定值,则变换矩阵只包括一个X'方向平移变换和绕Z'轴的旋转角度α变换,可以通过计算得出总变换矩阵Tprz,使得新坐标系内所有点满足:
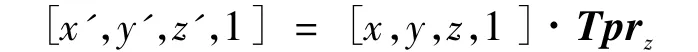
式中:Tprz=Tp·Trz,Tp 和 Trz分别为:

(3)数学模型。将离散后的曲臂每一个网格单元看作一个质点,其坐标用单元质心坐标表示,则第 i个质点坐标为(xi,yi,zi),质量 mi= ρvi,在动平衡计算中,所产生的离心惯性力Fi=miω2ri,每个平衡基面上的质心向径相等,即:ri=rⅠ=rⅡ。
在平衡面Ⅰ内:
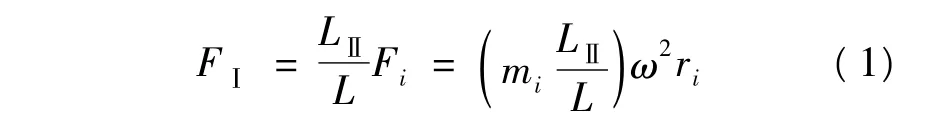
在平衡面Ⅱ内:

因此,当曲臂满足动平衡时,只需要在两个平衡面内有:
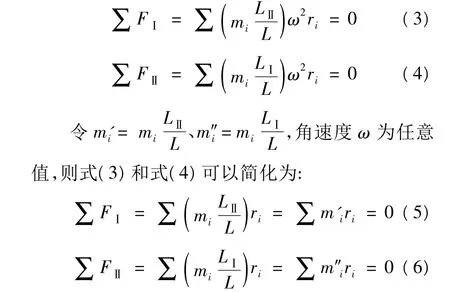
3.3 曲轴成品质量中心定位算法的实现
在Matlab软件中,通过编制程序建立以上数学模型[10],在给定范围内迭代搜索合适的总变换矩阵参数,满足Y'轴为曲臂处于动平衡时的质量中心轴线。根据以上分析,设定边界条件为:
(1)平移量 X0∈(235,245),搜索步长为0.001,默认单位为mm,Y0为原点在曲轴毛坯左轴端面的坐标值,即Y0=90.127;Z0为对称面的坐标值,即Z0=-704.850。
(2)绕 Z 轴旋转角度 α∈(-15°,15°),弧度表示为 α∈(-0.262,0.262),搜索步长为0.001。
根据式(5)和式(6)动平衡条件,判定迭代搜索跳出的条件为各个平衡基面内的分力为0,即优化目标为:
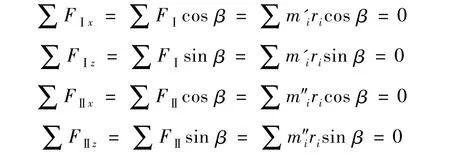
程序计算结果为X0=239.161,α=0.004(弧度),即为0.23°,表明曲轴成品质量中心轴线Y'轴通过原坐标系下的某一定点O'(239.161,90.127,-704.850),且与水平线的夹角为0.23°。
3.4 曲轴成品的三维模型重构
曲轴成品三维模型的建立,需要考虑曲轴的加工工艺,以曲轴成品质量中心轴线为旋转轴,重构各个主轴颈,然后利用轴颈中心距为定值的特性,重构各个连杆颈。
对于实验中的四缸铸造曲轴,考虑加工余量,圆整后得到曲轴成品的主轴颈半径为43 mm,连杆颈半径为35 mm。在毛坯的点云数据中测量出曲轴毛坯的轴颈中心距d=64.506 mm,因此依据上述分析得到曲轴成品的三维模型如图6所示。
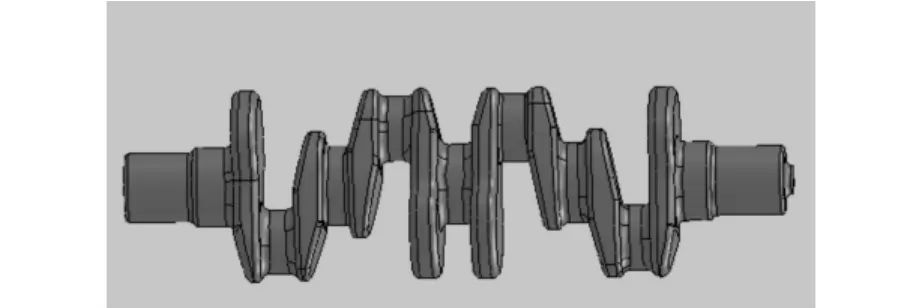
图6 成品曲轴的三维模型
4 结论
笔者提出曲轴成品质量中心定心方法,并以四缸曲轴毛坯为例对这种新定心工艺的算法进行了研究。研究结果表明,根据曲轴毛坯的三维几何信息,可预测曲轴成品的回转质量中心,实现曲轴成品质量中心的定心工艺方法。与现有的定心方法相比,该方法有着诸多优点。
[1]彭文生,李志明,黄华梁.机械设计[M].北京:高等教育出版社,2002:400-404.
[2]孟少龙.机械加工工艺手册[M].第1卷.北京:机械工业出版社,1991:3-14.
[3]于涛,仲继明,王海峰.曲轴定心与动平衡技术的探讨[J].汽车技术,2006(5):39-42.
[4]罗军民.曲轴中心孔加工方式的选择与研究[J].汽车科技,1997(4):1-6.
[5]朱正德.曲轴定心工序工艺的运行[J].汽车工程师,2009(8):41-44.
[6]陈元琰,张睿哲,吴东.计算机图形学实用技术[M].北京:清华大学出版社,2007:165-170.
[7]孙文磊,黄艳华.大尺寸复杂零件逆向重构再设计应用研究[J].机械设计,2008(10):49-50.
[8]谢龙汉,单岩.CATIA V5逆向造型设计[M].北京:清华大学出版社,2004:67-72.
[9]博弈创作室.ANSYS 9.0经典产品高级分析技术与实例详解[M].北京:中国水利水电出版社,2005:41-43.
[10]王沫然.Matlab与科学计算[M].北京:电子工业出版社,2004:169-177.

