相对误差直线回归模型两种参数估计方法的比较
刘成友 丁 勇
相对误差直线回归模型两种参数估计方法的比较
刘成友1丁 勇2△
1.南京医科大学生物医学工程系(210029)
2.南京医科大学数学与计算机教研室(210029)
△通讯作者:丁勇,E-mail:yding@njmu.edu.cn
最小二乘法的原理是观察值与拟合值的绝对误差平方和最小,其评价依据是针对等精度数据而言的,即观测数据具有大体相同的绝对误差,这些误差服从均值为0的正态分布。然而大量的科学研究的观测数据的误差往往是相对误差,即被观测量愈大,允许的实际观测误差也愈大。例如,医学应用中,浓度测定的标准曲线,样品测定的准确度和精度是以相对误差为依据的,这样的数据用通常的最小二乘法将导致参数估计的不准确,因此,以相对误差最小为原理的直线回归的方法应运而生〔1-8〕。
目前有两种以相对误差平方和最小为原理的求直线回归的方法〔2-7〕,本文对这两种方法进行比较和评价,为实际应用选择较好的方法提供依据。
原理和方法
1.a、b的两种估计方法
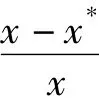
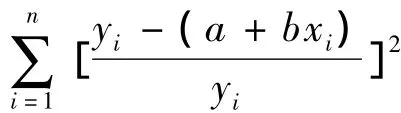
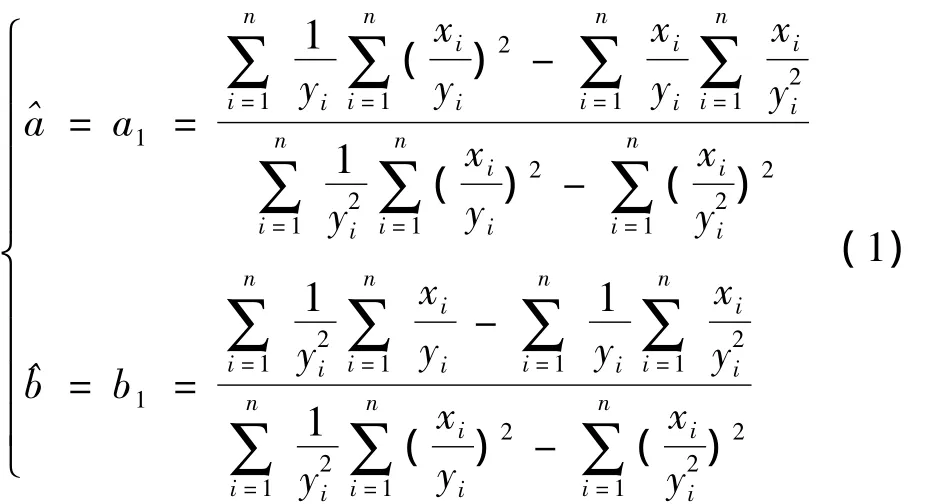

实际计算时,要先估计a、b的一个初始值、,再用上述公式进行迭代。当前后两次的迭代值小于给定的精度ε时,即ε、|<ε时,停止迭代。将最后一次的计算结果作为a、b的估计值,即取a=a2、b=b2。
用哪一种方法估计a、b较好呢?这是本文要讨论的问题。
2.正态分布的方差和观察数据的相对误差限
绝对误差服从正态分布的回归模型为〔9〕:
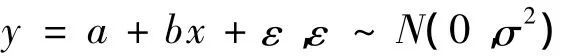

我们将这种模型称为绝对误差回归模型。
相对误差服从正态分布的回归模型可表示为:
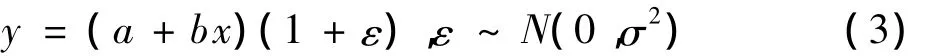
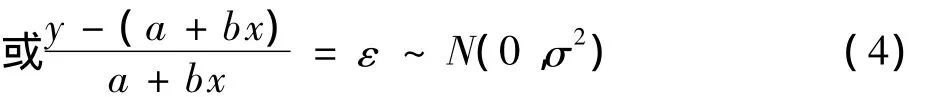
我们将这种模型称为相对误差回归模型。
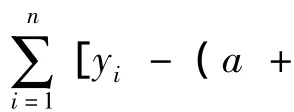
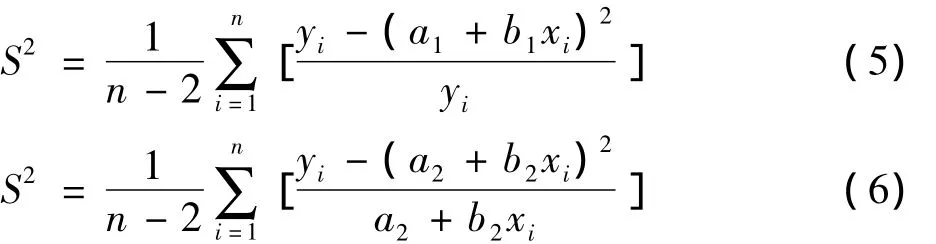
即用相对残差平方和对总体方差进行估计。
再来推导观察数据相对误差限与正态分布方差的关系。设X~N(μ,σ2),由正态分布的 3σ 原则〔9〕可知,P{|X-μ|≤3σ}=0.9973,这里我们可将3σ 视为绝对误差限。
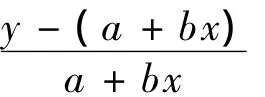

上式给出了相对误差模型中标准差与观察数据的相对误差限的关系。
在此基础上,可用计算机进行模拟计算。通过模拟计算,对两种方法进行比较、评价。
模拟比较
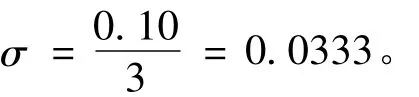
取a=5,b=10,自变量x=1,2,…,10,用计算机产生ε~N(0,0.03332)随机数作为相对误差,按公式(3)得到对应的因变量y,分别用如下两种方法估计各参数,共进行了1万次模拟,计算结果的均值见表1。
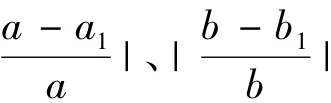
方法2:将用方法1求出的a1、b1作为初值、,再用公式(2)进行迭代,当前后两次参数值的差小于 ε=0.00001时,停止迭代。再用计算a2、b2的相对误差,再用(6)式求出S=
再分别取a=5、b=5 和a=10、b=5,用上述类似的方法,求出各参数,结果列于表1。
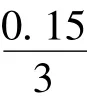
所有模拟和计算,用MATLAB 7.0编程完成。
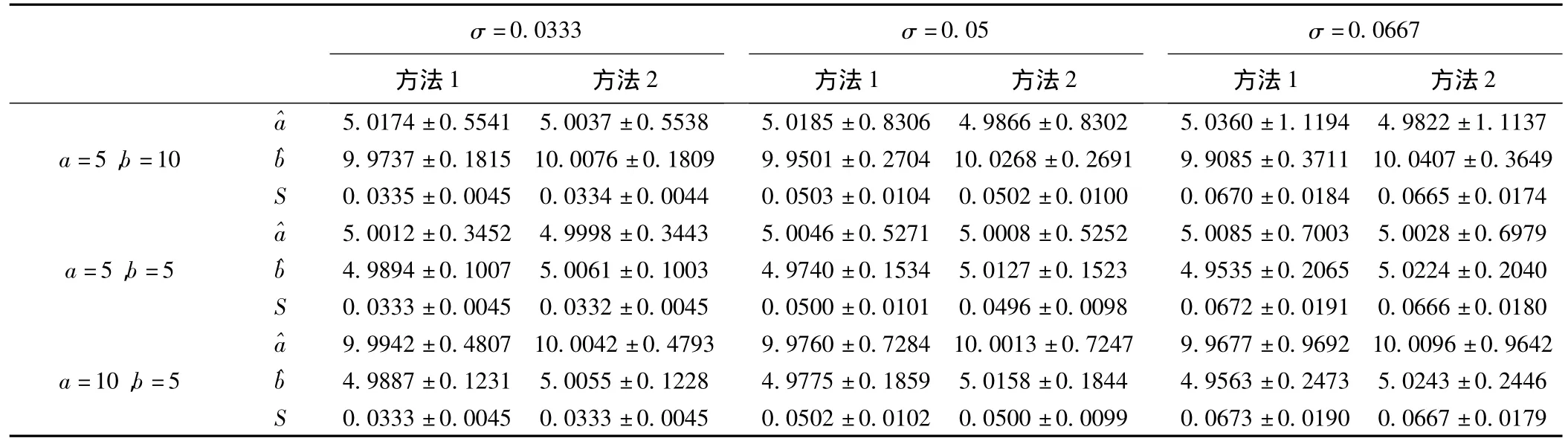
表1 两种方法参数估计的比较(¯x±s,10000次模拟结果)
讨 论
在实际应用中,大量数据的相对误差服从正态分布,这样的数据不宜用通常的最小二乘法估计参数,而应该用以相对误差最小为原理的方法估计参数。
本文揭示了正态总体方差与相对残差平方和、观察数据相对误差限之间的关系,推导了公式(5)~(7),从而为计算机模拟和σ2的估计提供了方法。
我们针对a<b、a=b和a>b,设计了表1中3种不同情况的模拟。由表1可知,随着相对误差(对应于σ)的增大,参数估计的误差也增大。无论哪种情况,a(截距)的误差要比b(斜率)的误差大些。在实际问题中,要求观察数据的相对误差不能太大,否则失去应用价值。在我们的模拟过程中,设计了3种相对误差限,来考察计算方法的稳健性,由表1可知,即使相对误差较大(20%,对应于σ=0.0667),两种方法计算的结果还都是可靠的。
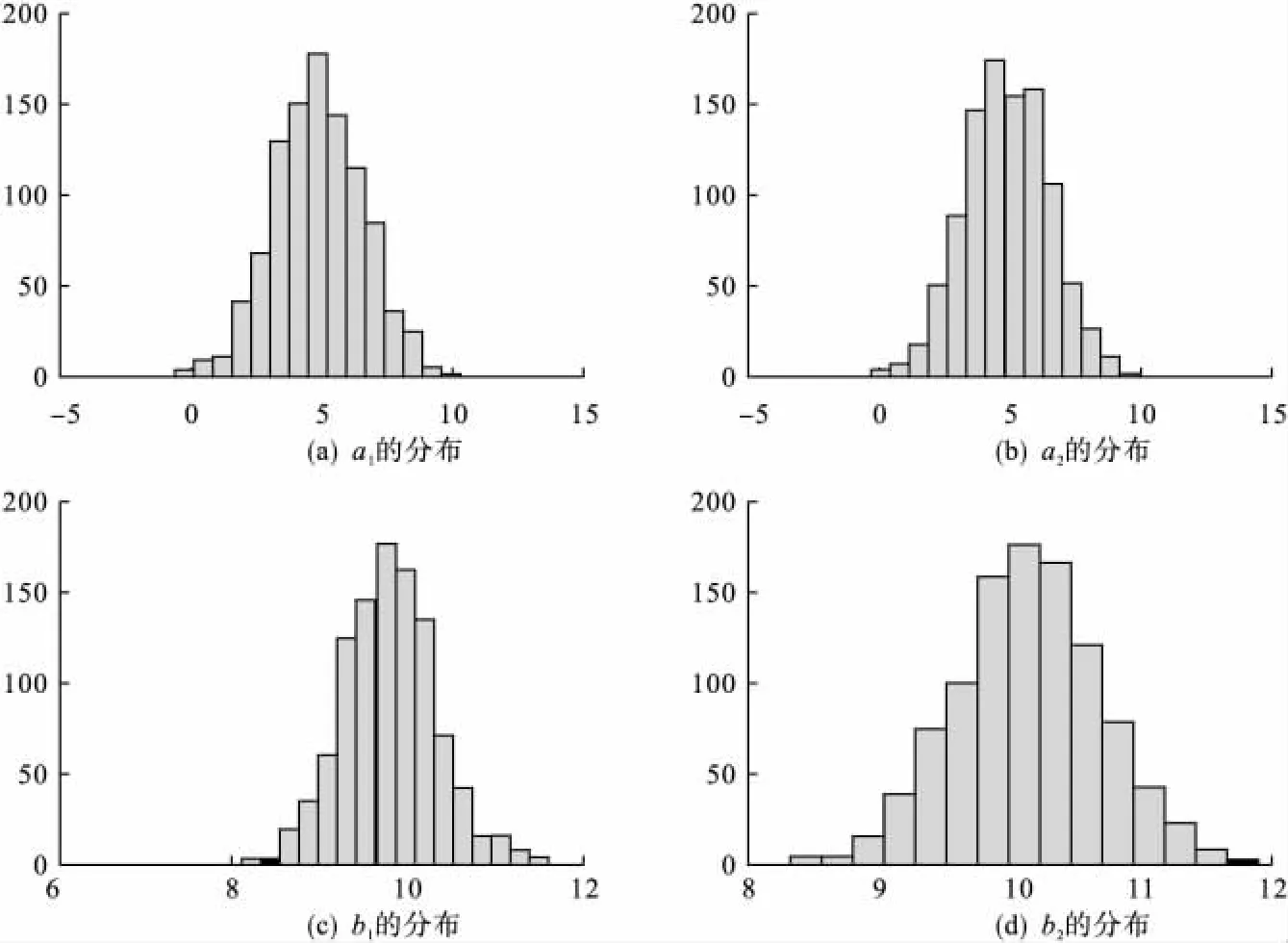
图1 参数分布图(σ=0.0377,a=5,b=10)
本文用模拟数据进行了统计分析:图1为σ=0.0377、a=5和b=10时,两种不同算法a、b估计值的4幅分布直方图。表1的9种情况,共有36幅分布直方图,绝大多数都服从正态分布(用Lilliefors正态检验法〔10〕,有5幅不服从正态分布;用Jarque-Bera正态检验法〔11〕,有4幅不服从正态分布);比较表1的σ和S可知,用公式(5)或(6)对总体方差σ2进行估计还是比较准确的。
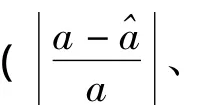
1.Narvla SC,Wellington JF.Prediction,linear regression and the minimum sum of relative errors.Technometrics,1977,19(2):185-191.
2.成军,孙关忠,李早荣,等.相对残差法线性回归与相关的理论研究:回归模型的建立及实验分析.中国卫生统计,1996,13(3):37-39.
3.成军,孙关忠.相对残差法线性回归与相关的理论研究:回归分析、相关模型及其假设检验.数理医药学杂志,1999,12(3):200-201.
4.成军,孙关忠,李早荣.现行线性回归理论的局限性及相对残差线性回归法在医学检验中的应用价值.陕西医学检验,2000,15(1):62-64.
5.李成思.基于相对误差意义下的最小二乘法.数理统计与管理,2003,22(4):36-40.
6.Arnold B,Stahlecker P.Relative squared error prediction in the generalized linear regression model.Statistical Papers,2003,44(1):107-115.
7.云连英,曹勃.基于优化的相对误差意义下的数据拟合.统计与决策,2007,21:15-16.
8.Tong TJ,Liu AN,Wang YD.Relative errors of difference-based variance estimators in nonparametric regression.Communications in Statistics:Theory and Methods,2008,37(18):2890-2902.
9.祝国强.医药数理统计方法.第2版.北京:高等教育出版社,2009,228-230,97,39-42.
10.Conover WJ.Practical nonparametric statistics.New York,Wiley,1980.
11.Judge GG,Hill RC,Griffiths WE,et al.Introduction to the theory and practice of econometrics.New York,Wiley,1988.

