基于数值inf-sup条件的US-FE-LSPIM四边形单元稳定性研究

贾 程，陈卉卉

(盐城工学院土木工程学院，江苏盐城224051)

0 引言

在过去的几十年中，有限单元法已经广泛应用于工程计算领域.但是，使用传统的等参有限元模型精度较低，在畸变的网格下结果较差.为提高有限单元法的精度，学者们做了大量的研究工作.

Wilson等［1］通过引入内部参数，提出了著名的四节点非协调Q6单元.Simo［2］在1990年提出了增强假设应变法(EAS)，应变域中引入了由额外的内部域变量产生的应变.龙驭球等［3］建立了四边形面积坐标理论，提出了许多高质量的单元.无网格方法由于不需要网格离散问题域，而且具有精度高、应力连续的特点.因此，近些年来涌现出许多种无网格方法，例如无网格伽辽金法(EFG)［4］、点插值法(PIM)［5］等.由于无网格法形函数不具有Kronecker-delta性质，使得直接施加本质边界条件比较困难.

为了构建高精度单元，最近 Rajendran等［6］结合有限单元法和无网格法的优点，提出了FELSPIM QUAD4单元.该单元属于杂交单元.与有限单元法相比，它的优点是FE-LSPIM单元的形函数对网格畸变不敏感.但是，该单元施加单元整体边界需满足的位移不方便，需要用罚函数或拉格朗日乘子法.

针对 FE-LSPIM四边形单元的不足，文献［7－8］提出US-FE-SPIM QUAD4单元.该单元由不同的形函数集作试函数和检验函数而构成.传统的等参形函数集作为检验函数，能够满足单元内和单元间的位移连续性要求;使用FE-LSPIM QUAD4单元［6］形函数作为试函数，能够满足所有位移完备性要求.该单元优于传统的四边形等参单元Q4和QM6单元，显示了良好的抗网格畸变性，并且能方便地施加整段长度的位移边界条件.

一致性和稳定性是保证有限元收敛的两个重要要求.一致性要求确保随着网格细分，单元的尺寸趋于0时，有限元的解趋于精确解.一致性要求可以通过选择连续的检验函数和试函数满足.文献［8］使用常应变分片检验和线性应变分片检验算例，证明US-FE-SPIM四边形单元满足一致性要求.稳定性要求需要满足著名的Babuska-Brezzi条件［9］(BB条件)，BB条件又称 inf-sup条件.对于给定的网格划分，检验inf-sup条件能够为评估一个单元的稳定性和精度提供必要的信息.

笔者进一步研究US-FE-SPIM四边形单元的数值收敛稳定性，推导出了该单元数值化的infsup条件表达式.通过数值的方法，检验该单元是否满足inf-sup条件.典型算例表明，该单元能通过数值inf-sup检验，满足稳定性要求，确保该单元数值结果的收敛性.

1 US-FE-SPIM四边形单元

1.1 FE-LSPIM四边形单元的形函数

单元内位移u写成

式中：N'=[N1N2N3N4]，Ni，i=1，2，3，4 是四边形等参元形函数.

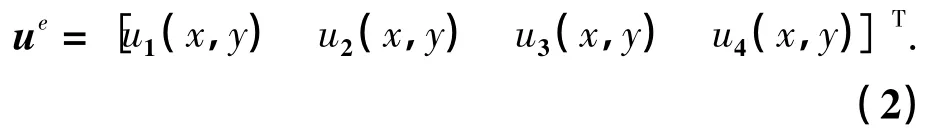
ui(x，y)，i=1，2，3，4，为节点位移函数，在该节点处等于其位移值，即：ui(xi，yi)=ui，i=1，2，3，4位移函数ui(x，y)由i点的支持域内的节点值运用最小二乘点插值法(LSPIM)得到，

节点支持域和单元支持域的定义如图1所示.

图1 支持域的定义Fig.1 Definition of the support

设单元支持域Ω内的节点数为M，则1≤N≤M，方程(3)就可以写成单元支持域的形式：

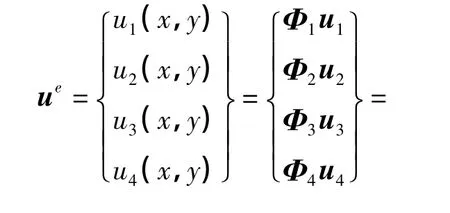
式中：Φ是相应于单元支持域的LSPIM单元形函数矩阵;u是单元支持域内所有节点的x方向的位移向量.为了方便起见，方程(4)中Φ的前四列为该单元的4个节点，其它列则是该支持域内的其他点.

将式(4)带入式(1)得

从式(5)中，得到该单元的形函数矩阵：

Φ中的元素Φi可以由i点的支持域内的节点值运用最小二乘点插值法(LSPIM)得到

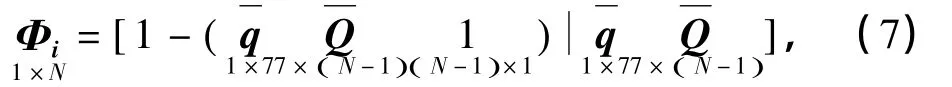
1.2 US-FE-SPIM四边形单元

线弹性体在平衡状态下的虚功方程为

式中：b为体力，t为面力，δu是虚位移场，δε 是相应的虚应变场，σ为真实的应力场.

FE-LSPIM四边形单元形函数Ψ能够满足高阶单元形函数完备性条件［10］，而常规的四边形等参元形函数只能满足低阶的条件.

由于式(8)中的虚位移可以是任意的，只要它满足本质边界条件和域内连续性条件.故常规的四边形等参元形函数插值的位移、应变是个合适的选择.应力试函数选择由FE-LSPIM四边形单元形函数插值的应力场.将它们代入式(8)中，经整理(见文献［7］)可得系统方程为

2 inf-sup条件

有限元公式保持数值稳定需要满足inf-sup条件.

对于线弹性椭圆边值问题，求u∈U，使得

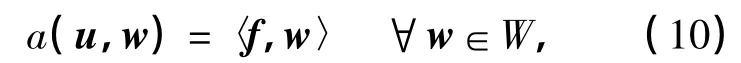
则inf-sup条件为

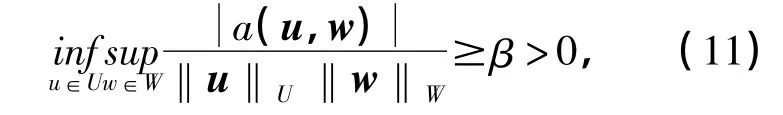
式中：β是与网格细分以及边界条件无关的常数，称为BB inf-sup常数.U，W为Hilbert空间，对于U：

W 类似.a(·，·)：U ×W→R是双线性型.L2(Ω)为Ω上二次可积函数空间.‖u‖U和‖w‖W分别是定义在空间U，W上的范数，笔者采用半范数［11］，对于‖u‖U：

但是，通过解析的方法获得BB inf-sup常数β较为困难，故笔者采用数值的方法寻找β的估计值，检验单元是否满足inf-sup条件［9］：如果某个问题在网格细分情况下β的估计值稳定收敛于正值，那么这种单元就通过数值inf-sup检验，满足inf-sup条件，表明该单元稳定.

对于给定的网格划分，方程(11)的有限单元形式为

式中：βh称为 inf-sup值，是β的估计值;U和W是位移向量;对于US-FE-SPIM四边形单元;K为整体刚度矩阵;SW和SU为整体范数矩阵，它由相应的单元范数矩阵组装成，即

N为有限元形函数矩阵;Q为FE-LSPIM四边形单元形函数矩阵;G为微分算子矩阵.

可以证明［11］其中 λ 是下面min特征问题去掉零特征值的最小特征值.

3 检验算例

3.1 正方形板

如图2所示，受两类边界条件的正方形板，用四个单元组成的超单元(如图3)划分模型，分别采用1×1，2×2，4×4，8×8个超单元划分.图2中模型采用了2×2规则网格划分.对于畸变网格划分，情况类似.弹性模量 E=2.1×1011，泊松比μ=0.3，采用2×2高斯积分，考虑平面应力情况.

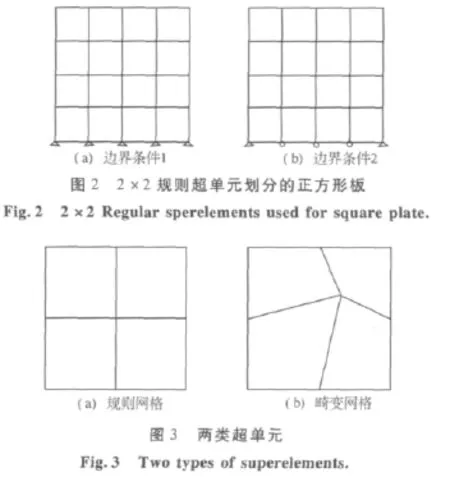
图4～图5绘出了LOG10(inf-sup值)－LOG10(1/N)曲线图，其中N为板长方向的网格数.从图中可以看出，在两类边界条件下，规则网格和畸变网格的inf-sup值都能稳定收敛于一个正值.

图4 正方形板边界条件1的inf-sup值收敛性Fig.4 Convergence of inf-sup value for square plate with the boundary condition 1.

图5 正方形板边界条件2的inf-sup值收敛性Fig.5 Convergence of inf-sup value for square plate with the boundary condition 2.

3.2 Cook悬臂梁

如图6所示，右端边界受分布剪力的变截面悬臂梁.采用2×2，4×4，8×8，16×16的网格划分模型.泊松比μ为1/3，弹性模量E=1.边界条件1为左边界节点约束x，y方向位移，边界条件2为左右两边界节点约束x，y方向位移.

图6 Cook悬臂梁Fig.6 Cook’s skew beam.

图7绘出了LOG10(inf-sup值)－LOG10(1/N)曲线图.

图7 Cook悬臂梁的inf-sup值收敛性Fig.7 Convergence of inf-sup value for Cook’s skew beam

从图上可以看出，对于边界条件1和2，infsup值都能稳定收敛于一个正值.

3.3 厚弯曲梁

对图8厚弯曲梁分别采用2×4，4×8，6×12，8×16的网格划分，弹性模量 E=1.0×107，泊松比μ=1/3，厚t=1.图9绘出了不同高斯积分时的LOG10(inf-sup值)－LOG10(1/N)曲线图.

从图上可以看出，对于2×2和3×3高斯积分inf-sup值都稳定收敛一个正值.

4 结论

进一步研究了US-FE-SPIM四边形单元的数值收敛的稳定性.由于通过解析的方法验证一种单元是否满足inf-sup条件较为困难，利用数值的方法，推导出了US-FE-SPIM四边形单元数值化的inf-sup条件表达式，检验该单元是否满足infsup条件.典型算例表明，该单元在不同的边界条件、规则和畸变网格以及不同高斯积分方案下，其inf-sup值都能稳定的收敛于一个正值，能通过数值inf-sup检验，满足单元的稳定性要求.US-FESPIM四边形单元满足一致性和稳定性要求，确保了该单元数值结果的收敛性.数值化的inf-sup条件表达式为检验单元的稳定性提供了简便的途径.

［1］WILSON E L，TAYLOR R L，DOHERTY W P，et al.Incompatible displacement modes［C］.New York：Academic Press，1973.

［2］SIMO J C，RIFAI M S.A class of mixed assumed strain methods and the method of incompatible modes［J］.International Journal for Numerical Methods in Engineering，1990，29(8)：1595 －1638.

［3］龙驭球，李聚轩，龙志飞，等.四边形单元面积坐标理论［J］.工程力学，1997，14(3)：1－11.

［4］BELYTSCHKO，LU Y Y，Gu L.Element free Galerkin methods［J］.International Journal for Numerical Methods in Engineering，1994，37(2)：229 －256.

［5］LIU Gui-rong，GU Yuan－tong.A point interpolation method for two dimensional solid［J］.International Journal for Numerical Methods in Engineering，2001，50(4)：937－951.

［6］RAJENDRAN S，ZHANG B R.A“FE-Meshfree”QUAD4 element based on partition of unity［J］.Computer Methods in Applied Mechanics and Engineering，2007，197(1 －4)：128－147.

［7］贾程，陈国荣，陈卉卉.US-FE-SPIM四边形单元的自由振动研究［J］.郑州大学学报：工学版，2009，30(2)：129 －132.

［8］贾程，陈国荣，陈卉卉.US-FE-SPIM四边形单元及其在几何非线性问题中的应用［J］.计算力学学报，2011，28(5)：785 －791.

［9］CHAPELLE D，BATHE K J.The inf-sup test［J］.Computers and Structures，1993，47(4/5)：537 －545.

［10］RAJENDRAN S，LIEW K M.Completeness requirements of shape functions for higher order finite elements ［J］.Structural Engineering and Mechanics，2000，10(2)：93 －110.

［11］BATHE K J，HENDRIANA D，BREZZI F，et al.Infsup test of upwinding methods［J］.International Journal for Numerical Methods in Engineering，2000，48(5)：745 －760.