BFRP筋混凝土双向板冲切承载力塑性分析
朱海堂,王怡中,李金章
(郑州大学水利与环境学院,河南郑州450001)
0 引言
混凝土双向板作为港口工程中应用最为广泛的结构形式之一,由于自重和承受的荷载较大,板中产生巨大的冲切作用,出现大面积裂缝从而引起钢筋锈蚀,严重影响结构的承载能力和耐久性能.新型复合材料纤维增强聚合物筋(Fiber Reinforced Polymer Rebars,简称FRP筋)具有非常良好的抗腐蚀性能[1].以FRP筋代替钢筋应用于海洋等腐蚀环境中的混凝土结构中,将使得结构具有较好的耐久性能,降低后期维修成本.同时,FRP筋密度较小的特点能够有效减少结构自重.因此,研究FRP筋混凝土双向板的冲切性能对于港口或地下工程建设具有重要意义.
目前,关于FRP筋混凝土板尤其是双向板的研究工作开展得较少[2-7],国内外还没有形成一个关于FRP筋混凝土双向板设计的相关规定.在加拿大标准协会规范 CSA S806—02[8]中虽给出了FRP筋混凝土单向板受弯构件的剪切设计公式和双向板的设计建议,但由于缺乏FRP筋混凝土双向板冲切性能的研究,给出的FRP筋混凝土双向板的设计建议只是基于钢筋混凝土双向板的试验结果.然而,钢筋混凝土双向板的设计主要以钢筋的屈服为设计基础,而FRP筋是一种无屈服点的线弹性材料,其弹性刚度、极限抗拉强度和粘结性能与钢筋有较大不同,但这些参数对FRP筋混凝土双向板的冲切性能及其承载力有显著影响,因而直接采用钢筋混凝土双向板的计算方法对FRP筋混凝土双向板进行设计显然是不适当的.
基于此,笔者在BFRP(Basalt Fiber Reinforced Polymer,简称BFRP)筋混凝土双向板冲切性能试验研究的基础上,对中置集中荷载作用下的BFRP筋混凝土双向板冲切性能进行极限承载力的塑性理论分析,提出适合BFRP筋特点的BFRP筋混凝土双向板冲切承载力计算方法.
1 BFRP筋混凝土双向板材料的本构关系
1.1 混凝土本构关系
假定混凝土为理想的刚塑性材料,采用有效抗拉强度和有效抗压强度分别表示其抗拉、抗压的能力,f't=vtft,f'c=vcfc,其中,vt,vc为小于 1 的折减系数.对于普通的混凝土vt=vc=0.35.
1.2 BFRP筋本构关系
混凝土应力—应变关系如图1所示,BFRP筋应力-应变关系如图2所示.BFRP筋是一种线弹性材料,在整个受力过程中不存在屈服平台,几乎没有发生塑性变形,其实际的应力-应变关系如图2(a)所示.在进行BFRP筋混凝土双向板冲切承载力的塑性极限分析时,参考无屈服点钢筋的条件屈服点定义,采用BFRP筋名义屈服强度ffy来反映BFRP筋在混凝土板发生塑性屈服时的抗拉能力,认为BFRP筋在达到名义屈服强度后其应力值不再增加,但应变继续增大,其简化的理想塑性应力应变关系如图2(b)所示.BFRP筋名义屈服强度是对其极限抗拉强度的一个折减,ffy=φσfu,其中φ是一个小于1的折减系数.

2 BFRP筋混凝土双向板的冲切破坏机构与破坏准则
2.1 破坏机构
根据文献[6],中置集中荷载作用下的BFRP筋混凝土双向板在受力之初以受弯为主,具有一定的弯曲变形,而在最终破坏时形成冲切锥体从板中冲出,呈冲切破坏特征.图3为试验结束后混凝土板底面的破坏形态.
根据图3的破坏形态,参照文献[9],中置集中荷载作用下的BFRP筋混凝土双向板的冲切破坏机构如图4所示.图中,加载边长为d,假设破坏面是一个以直线为母线的锥面,破坏面是由板上部加载面边与板底部的连线,母线与垂直方向的夹角为β;假定图中Ⅰ区和Ⅱ区是刚性区,Ⅲ区是塑性区,冲切破坏时Ⅰ区与Ⅱ区之间发生明显的相对错动,但在最终破坏前板已经有一定的弯曲变形;θ是冲切锥形成时板面变形的倾角,通过对试验板的实验观察和试验结果的分析,该角为6°左右[6].
2.2 破坏准则
分析采用俞茂宏的双剪统一强度理论[10],该理论的突出特点就是采用两个主剪应力作为判断材料破坏(或屈服)的准则,认为在任一点的应力状态中存在3个主剪应力,只要考虑其中2个主剪应力,即可全面反映该点的应力状态,可以反映材料在多轴应力状态下的强度性能.笔者以双剪统一强度理论为依据推导轴对称条件下BFRP筋混凝土双向板冲切破坏时极限承载力的计算公式.

双剪统一强度理论破坏准则的表达式为

对于轴对称问题,采用刚塑性模型[11],设位移场轴对称,则有

由此可得

将式(2)代入式(1),可以得到在轴对称条件下的双剪统一强度理论公式为

可以验证,当σ1>0时,恒满足条件(1),所以采用条件(1)作为破坏判别准则.

3 极限应力圆包络线方程
设破坏面上一点的正应力为σn,剪应力为τn,则极限应力圆(如图5)方程为

将式(4)代入式(5)得
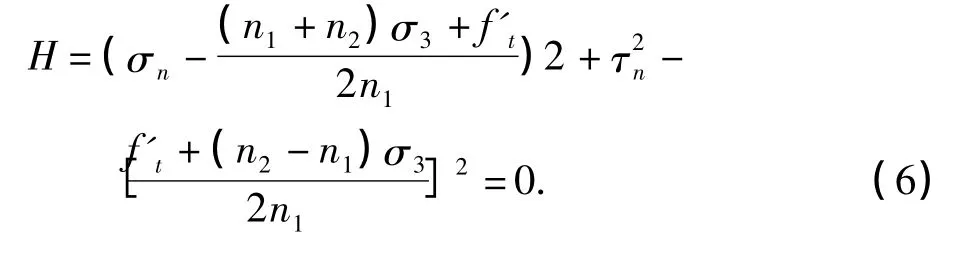

图5 极限应力圆包络线Fig.5 Failure envelope of ultimate stress circle

所以

将式(8)代入式(6)即得极限应力圆的包络线方程为

将式(6)代入式(10)得
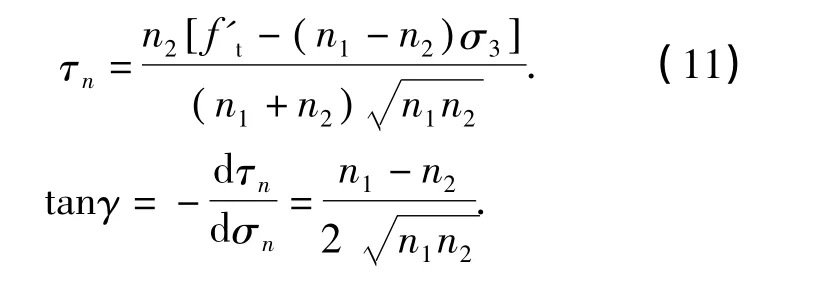
4 BFRP筋混凝土双向板的冲切承载力
根据虚功原理,外力所做的外功等于板冲切承载力所做的内功,而板的冲切极限承载力由混凝土和BFRP筋共同提供,承载力的内虚功等于混凝土所做的内功与BFRP筋所做的内功之和.假设混凝土板在外荷载P的作用下,发生大小为u的位移,可能的机动位移场如图6所示,其中,n和t分别代表锥体母线的法线方向和切线方向;δ为塑性区Ⅲ的初始厚度;u为中心锥体Ⅰ在柱荷载下发生的虚位移;β为屈服面与竖直方向位移的夹角.

图6 冲切锥的位移场Fig.6 Deformation field of slab under punching shear
4.1 混凝土所作的内功
对应于位移u的混凝土的应变为:

由塑性流动法则可知:

所以:β=γ.
混凝土的虚功为:

将式(9)、(11)、(12)和(13)代入式(14)可得:

4.2 BFRP筋所作的内功
假定在板的整个受力过程中,BFRP筋与混凝土保持共同变形,在混凝土板发生冲切破坏时,与塑性区相交的BFRP筋达到其名义屈服强度ff,则BFRP筋所作的内功为:

式中:σf为与混凝土塑性区相交的BFRP筋的应力值,即:σf=ff;εf为对应于位移u的BFRP筋的应变值为与塑性区相交的BFRP筋的总的截面面积,Af=πρ( d+2h0tanβ )h0,ρ为BFRP筋混凝土板的配筋率;d是加载面的边长;h0是混凝土双向板的有效厚度.

4.3 BFRP筋混凝土双向板的冲切承载力
设冲切承载力为P,则外力P所做的虚功为:

由虚功原理,外力的虚功等于内力的虚功,即:

将式(15)、(16)和(17)代入式(18),则有:

于是,中置集中荷载作用下BFRP筋混凝土双向板极限冲切承载力的表达式为:

5 结论
(1)根据中置集中荷载作用下BFRP筋混凝土双向板的冲切破坏形态及其破坏特征,建立了基于塑性理论分析的中置集中荷载作用下BFRP筋混凝土双向板的破坏机构,提出了相应的破坏准则;结合BFRP筋材料的性能特点,采用BFRP筋名义屈服强度,提出了基于塑性理论分析的中置集中荷载作用下BFRP筋混凝土双向板极限冲切承载力的计算表达式.
(2)所提出的BFRP筋混凝土双向板极限冲切承载力的塑性解计算表达式中的系数n1、n2等系数受到α、b等取值的影响,系数θ的取值对分析计算结果也将具有显著影响.由于BFRP筋混凝土双向板的冲切性能试验研究还很少,而系数α、b、θ的取值受到BFRP筋混凝土双向板的原材料特征参数、截面尺寸、板中配筋以及所采用的破坏准则等多方面的影响,尚需更为深入的试验研究和更为系统的理论分析才能确定.
[1]高丹盈,李趁趁,朱海堂.纤维增强塑料筋的性能与发展[J].纤维复合材料,2002,20(4):37 -40.
[2]MATTHYS S,TAERWE L.Concrete slabs reinforced with FRP grids.II:Punching resistance[J].Journal of Composites for Construction,2000,4(3):154 -161.
[3]GAMAL S,SALAKAWY E F,BENMOKRANE B.A new punching shear equation for two-way concrete slabs reinforced with FRP bars[C]//International Symposium on Fiber-Reinforced Polymer(FRP)Reinforcement for Concrete Structures.Kansas,2005,2:877-893.
[4]THEODORAKAPOULOS D D,SWAMY N.Analytical model to predict punching shear strength of FRP-reinforced concrete flat slabs[J].ACI Structural Journal,2007,104(3):257 -266.
[5]OSPINA C E,ALEXANDER S D B,ROGER C J J.Punching of two-way concrete slabs with fiber-reinforced polymer reinforcing bars or grids[J].ACI Structural Journal,2003,100(5):589 -598.
[6]肖志龙.中置集中荷载作用下FRP筋混凝土双向板冲切性能研究[D].郑州大学水利与环境学院,2010.
[7]张亚坤.偏置荷载下FRP筋砼双向板冲切性能研究[D].郑州大学水利与环境学院,2010.
[8]CSA.S806-02:Design and construction of building components with fibre-reinforced polymers[S].Mississauga,Canada:Canadian Standards Association;2002.
[9]林旭健,郑作樵,钱在兹.混凝土弯冲板的破坏机构与极限强度[J].工程力学,2003,20(1):58 -62,75
[10]俞茂宏.双剪理论及其应用[M].北京:科学出版社,1998.
[11]严宗达.用双剪强度理论解混凝土板冲切的轴对称问题[J].工程力学,1996,13(1):1 -7.

